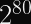Search
Items tagged with: SecurityGuidance
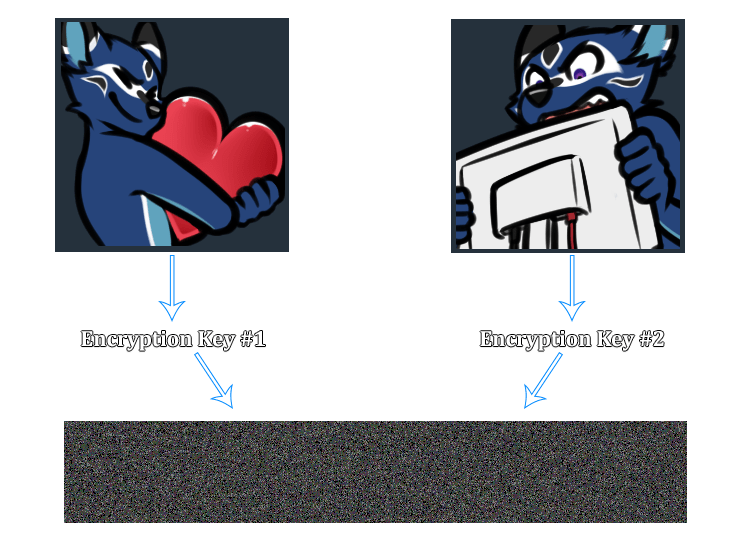
Since the IETF’s CFRG decided to recommend OPAQUE as a next-generation Password Authenticated Key Exchange, there has been a lot of buzz in the cryptography community about committing authenticated encryption (known to the more academically inclined as Random Key Robustness), because OPAQUE requires an RKR-secure AE scheme.
Random Key Robustness is a property that some symmetric encryption modes have, where it’s not feasible to decrypt a valid (ciphertext, tag) pair into two different plaintexts if both recipients are using different keys.
To illustrate this visually:
In the wake of the CFRG discussion, it became immediately clear that AES-GCM doesn’t meet this requirement.
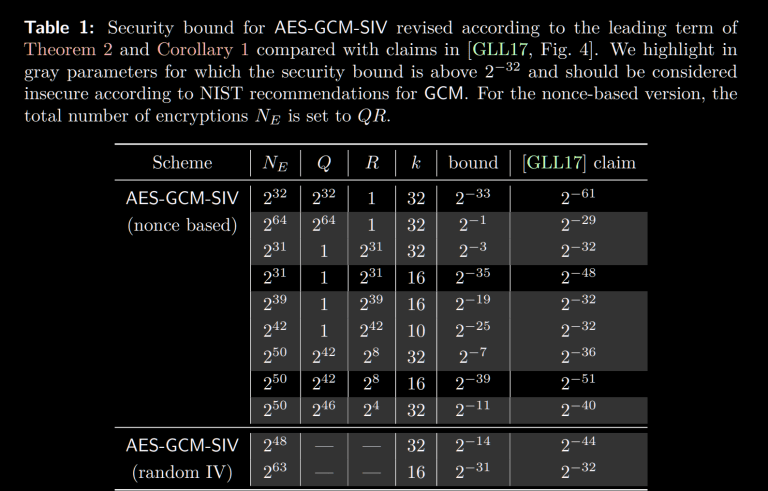
What wasn’t immediately clear is that AES-GCM-SIV also falls short. But don’t take my word for it, Sophie Schmieg worked out the math in the linked post, which I highly recommend reading.
This isn’t to say that AES-GCM or AES-GCM-SIV are doomed, or should be deprecated. You probably don’t even care about Random Key Robustness in most of the places you’d use either algorithm! But if you are doing something where RKR actually matters, you probably care a lot. And it certainly violates the principle of least astonishment.
ChaCha20-Poly1305 won’t save you here either, since this is a property that message authentication codes based on cryptographic hash functions (e.g. HMAC) provide, but polynomial MACs (GMAC, Poly1305, etc.) do not.
So, if every standardized and widely-supported AEAD construction fails to provide RKR security, what’s a software engineer to do?Roll their own crypto?!

If you’re always on a well-tread path with a well-defined, standard threat model (i.e. client-server application accessible via TLS 1.3, possibly storing hashed passwords server-side), then rolling your own crypto isn’t just dangerous; it’s wholly unnecessary.
Coping with Non-Standard Threat Models
Systems that require Random Key Robustness do not fall within the standard threat model of AEAD cipher constructions.
However, RKR is far from the only scenario in which application developers might find themselves without a clear solution. Another example that comes up a lot:
“I need to encrypt data in a relational database, but still somehow use it in SELECT queries.”— Far too many damn developers who haven’t heard of CipherSweet.
The first thing that you should do is clearly document your requirements and what attacks your system must protect against. Any undefined attack vector in your model should be assumed to be a vulnerability in your design. (This gets into Unknown Unknowns territory quickly.)
And then you should have a cryptographer review your design, and then have a cryptography engineer build it for you.
But where’s the fun in that?

Instead of copping out with sane and reasonable advice, let’s actually walk through the process. At the end of this post, I’ll share a toy example I cooked up for this blog post.
Designing New Cryptography
First, Understand the Problem
Why don’t AES-GCM, etc. provide Random Key Robustness? Because they’re built with universal hash functions rather than cryptographic hash functions.
Cryptographic hash functions have different properties (i.e. preimage resistance and collision resistance) that make it significantly difficult to calculate two different authentication tags under two different keys. Attacking HMAC-SHA-256 in this way is about as expensive as brute forcing a 128-bit AES key. (Good luck with that!)
However, cryptographic hash functions are much slower than polynomial MACs, and using them in a construction like HMAC approximately doubles the slowness.
You might be tempted to just hash they key and the message together to save on CPU cycles, but that’s actually not safe for the hash functions nearly everybody uses (due to length extension attacks).
It logically follows that, if we had an AEAD cipher construction based on a hash function, we could have RKR security.

Look At Prior Art
Before the days of AES-GCM and ChaCha20-Poly1305, there were a lot of ad hoc constructions used everywhere based on AES-CBC and HMAC. (In that era, everyone used HMAC-SHA1, but don’t do that.)
However, there are a number of problems with ad hoc CBC+HMAC that we don’t want to reintroduce in modern systems:
- If you forget to include the initialization vector in the HMAC tag, you give attackers free reign over the first 16 bytes of the decrypted plaintext without having to break the MAC.
- The order of operations (Encrypt-then-MAC, MAC-then-Encrypt, Encrypt and MAC) matters tremendously.
- CBC+HMAC is usually implemented in application-layer code, but the security of such a construction depends heavily on the availability and utilization of constant-time functions.
- There is no standard format for CBC+HMAC, nor the order of operations for what gets fed into the MAC.
- IV + ciphertext? Ciphertext + IV?
- Append the MAC, or prepend it?
- CBC+HMAC is only an AE mode, there is no room for additional authenticated data. If you try to naively shove extra data into the HMAC, now you have to worry about canonicalization attacks!
- CBC mode requires padding (usually PKCS #7 padding), whereas cipher modes based on CTR do not.
This is among the long list of reasons why cryptographers have spent the past decade (or longer) pushing developers towards AEAD modes.
Boring cryptography is good cryptography!

Make sure you clearly understand the risks of the components other constructions have used.
Sketch Out A First Draft
By now, it should be clear that if we have an Encrypt-then-MAC construction, where the MAC is based on a cryptographic hash function (e.g. SHA-256), we may be able to attain RKR security.
With that in mind, our sketch will probably look something like this:
- Encrypt(K1, M, N) -> C
- Where Encrypt() is AES-CTR or equivalent
- Auth(K2, C, A) -> T
- Where Auth() wraps HMAC-SHA2 or equivalent
- How we feed C and A into the underlying MAC is important
- ???? -> K1, K2
We still have to define some way of splitting a key (K) into two distinct keys (K1, K2). You never want to use a cryptographic key for more than one purpose, after all.
Key-Splitting and Robustness
Your encryption key and authentication key should be different, but they should also derived from the same input key! This is mainly to protect implementors from having independent keys and accidentally creating a forgery vulnerability.
There are several different ways you can split keys:
- Just use SHA-512(k), then cut it in half. Use one half for encryption, the other for authentication.
- Use HMAC-SHA256(k, c1) and HMAC-SHA256(k, c2), where c1 and c2 are distinct (yet arbitrary) constants.
- Use HKDF. This works with any secure cryptographic hash function, and was specifically designed for situations like this. HKDF also supports salting, which can be used to randomize our derived keys.
We can really pick any of these three and be safe, but I’d advise against the first option. HKDF uses HMAC under-the-hood, so either of the latter options is fine.
Can We Make it Faster?
What if, instead of HMAC-SHA256, we used BLAKE3?
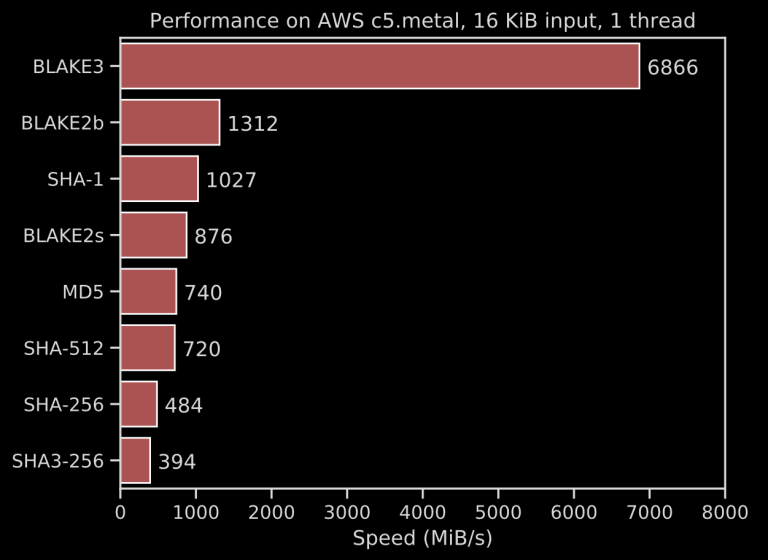
BLAKE3’s advertised 6.8 GiB/s can be even faster than Poly1305 or GHASH (and BLAKE3’s speed really shines through with long messages, due to its extreme parallelism through Merkle trees).
In Favor of ChaCha over AES
It’s no secret that I’m not a fan of AES. It’s not the mathematical properties of AES that bother me, it’s the 128-bit block size and the fact that software implementations have to decide between being fast or being secure.

ChaCha’s 256-bit security level is easier to justify: The underlying PRF state is 512 bits (which implies an approximately 256-bit security level) and the keys are always 256 bits.
Furthermore, if you’re building ChaCha and BLAKE3 in the same codebase, you could reuse some components (i.e. the compression function, G). This is very desirable if you’re trying to ship a small amount of code (e.g. embedded systems). EDIT: One of the BLAKE3 authors informed me that I’m mistaken about this: “[N]ope, not exactly the same logic (rotations in different direction)”.
Other Desirable Security Properties
Nonce Nonsense
One of the biggest problems with standard AEAD modes is that they explode gloriously when you reuse a nonce. There are two ways out of this peril:
- Use a nonce misuse resistant AEAD construction (AES-GCM-SIV, etc.).
- For prior art on nonce-misuse resistant cipher modes based on ChaCha, check out DAENCE.
- Use large nonces (e.g. XChaCha20 uses 192-bit nonces) and generate them randomly, so the probability of nonce reuse becomes negligible.
Since we’re already planning on using a hash function to derive subkeys (one for encryption, one for authentication), it makes sense to also accept a longer nonce than our stream cipher demands. The excess bytes can be passed to our KDF without significant risk or additional overhead.
Since the IETF’s ChaCha20 variant expects a 96-bit nonce, designing our construction to support 256-bit nonces means we can pass the first 160 bits of the nonce to the KDF and the latter 96 bits to the stream cipher. You can expect a single KDF collision after 2^80 encryptions, but it will almost certainly occur with a different nonce.
Safe MAC Canonicalization
We want to ensure it’s infeasible for an attacker to feed two different (ciphertext, AAD) pairs into our construction that produce the same tag.
Simply concatenating the two values will run the risk of someone shaving off a chunk of the ciphertext and storing it in the AAD instead.

The simplest solution is to either prepend or append the lengths of the components (as the little-endian octet string representation of 64-bit unsigned integers).
The choice between prepending and appending doesn’t affect security much, but appending the lengths is friendlier for streaming interfaces.
After all, in a streaming encryption/decryption interface, you might not know the lengths of the either component until you’ve finished encrypting and authenticating all of the data.

Putting It All Together
Now that we’ve meandered through a rough list of desirable design properties, let’s recap:
- We want to Encrypt then MAC.
- We want to use ChaCha20 (the IETF’s variant) as our stream cipher.
- We want to use keyed BLAKE3 for the KDF and MAC algorithm.
- We want to accept 256-bit nonces (160 bits for the KDF, 96 for the stream cipher).
- We want to ensure our ChaCha20 and BLAKE3-MAC keys are derived from the same input key, using some domain separation constants.
- We want to feed the data into the MAC this order:
- AAD
- Ciphertext
- Length of AAD
- Length of Ciphertext
- We want to ensure our authentication tags are always verified in constant-time.
That sounds like a lot. But what does it yield in terms of code size? Surprisingly very little!
You can find the JS implementation of my design on Github.
Should I Use This?

I mean, would your users really feel safe if you got your cryptography recommendations and implementations from a furry blogger?
This is just a toy example I put together for the sake of illustrating how a new cryptographic design might be proposed. That’s only the first step.
Ultimately, you shouldn’t use this for one simple reason: Neither my design nor my implementation have been peer reviewed.
Maybe I’ll refine it a bit and kick it over to the CFRG for consideration for inclusion with OPAQUE someday. It might turn out to be a good design. It might be vulnerable to some subtle attack I can’t even imagine right now.
Until experts tell you otherwise, it’s hazardous material and you should only play with it for educational purposes.

Further Reading
I’ve written a lot about cryptography, and there are always more topics to write about than I have the time or energy to cover, so here’s a few cool blogs/etc. to check out while I slog through Rough Draft Hell.
- Cryptography Dispatches — Newsletter ran by Filippo Valsorda, cryptographer and Go security team lead.
- Bulletproof TLS Newsletter — Newsletter ran by Hanno Böck, freelance journalist, IT security expert, and AES-GCM exploiter.
- Key Material — A new blog by Sophie Schmieg (cryptographer at Google) and Sarai Rosenberg (security engineer at Pager Duty).
- Little Man In My Head — A blog by Scott Contini, a security expert who frequently posts helpful comments on /r/crypto.
Header art by Khia. The figure in the background is from this paper on Message Franking via Committing Authentication Encryption.
https://soatok.blog/2020/09/09/designing-new-cryptography-for-non-standard-threat-models/
#BLAKE3 #ChaCha20 #cryptography #randomKeyRobustness #SecurityGuidance #symmetricCryptography
Authenticated Key Exchanges are an interesting and important building block in any protocol that aims to allow people to communicate privately over an untrusted medium (i.e. the Internet).What’s an AKE?
At their core, Authenticated Key Exchanges (AKEs for short) combine two different classes of protocol.
- An authentication mechanism, such as a MAC or a digital signature.
- Key encapsulation, usually through some sort of Diffie-Hellman.
A simple example of an AKE is the modern TLS handshake, which uses digital signatures (X.509 certificates signed by certificate authorities) to sign ephemeral Elliptic Curve Diffie-Hellman (ECDH) public keys, which is then used to derive a shared secret to encrypt and authenticate network traffic.
I guess I should say “simple” with scare quotes. Cryptography is very much a “devil’s in the details” field, because my above explanation didn’t even encapsulate mutual-auth TLS or the underlying machinery of protocol negotiation. (Or the fact that non-forward-secret ciphersuites can be selected.)
AKEs get much more complicated, the more sophisticated your threat model becomes.
For example: Signal’s X3DH and Double Ratchet protocols are components of a very sophisticated AKE. Learn more about them here.
The IETF is working to standardize their own approach, called Messaging Layer Security (MLS), which uses a binary tree of ECDH handshakes to manage state and optimize group operations (called TreeKEM). You can learn more about IETF MLS here.
Password AKEs
Recently, a collection of cryptographers at the IETF’s Crypto Research Forum Group (CFRG) decided to hammer on a series of proposed Password-Authenticated Key Exchange (PAKE) protocols.PAKEs come in two flavors: Balanced (mutually authenticated) and augmented (one side is a prover, the other is a verifier). Balanced PAKEs are good for encrypted tunnels where you control both endpoints (e.g. WiFi networks), whereas Augmented PAKEs are great for eliminating the risk of password theft in client-server applications, if the server gets hacked.
Ultimately, the CFRG settled on one balanced PAKE (CPace) and one augmented PAKE (OPAQUE).
Consequently, cryptographer Filippo Valsorda managed to implement CPace in 125 lines of Go, using Ristretto255.
I implemented the CPace PAKE yesterday with Go and ristretto255, and it felt like cheating.125 lines of code! Really happy with it and it was a lot of fun.
— Filippo Valsorda (@FiloSottile) March 29, 2020
Why So Complicated?
At the end of the day, an AKE is just a construction that combines key encapsulation with an authentication mechanism.But how you combine these components together can vary wildly!
Some AKE designs (i.e. Dragonfly, in WPA3) are weaker than others; even if only in the sense of being difficult to implement in constant-time.
The reason there’s so many is that cryptographers tend to collectively decide which algorithms to recommend for standardization.
(n.b. There are a lot more block ciphers than DES, Blowfish, and AES to choose from! But ask a non-cryptographer to name five block ciphers and they’ll probably struggle.)
https://soatok.blog/2020/04/21/authenticated-key-exchanges/
#ake #authenticatedKeyExchange #cryptography #ECDH

Earlier this year, Cendyne wrote a blog post covering the use of HKDF, building partially upon my own blog post about HKDF and the KDF security definition, but moreso inspired by a cryptographic issue they identified in another company’s product (dubbed AnonCo).
At the bottom they teased:
Database cryptography is hard. The above sketch is not complete and does not address several threats! This article is quite long, so I will not be sharing the fixes.Cendyne
If you read Cendyne’s post, you may have nodded along with that remark and not appreciate the degree to which our naga friend was putting it mildly. So I thought I’d share some of my knowledge about real-world database cryptography in an accessible and fun format in the hopes that it might serve as an introduction to the specialization.
Note: I’m also not going to fix Cendyne’s sketch of AnonCo’s software here–partly because I don’t want to get in the habit of assigning homework or required reading, but mostly because it’s kind of obvious once you’ve learned the basics.

If you don’t like furries, please feel free to leave this blog and read about this topic elsewhere.
Thanks to CMYKat for the awesome stickers.
Contents
- Database Cryptography?
- Cryptography for Relational Databases
- Cryptography for NoSQL Databases
- Searchable Encryption
- Order-{Preserving, Revealing} Encryption
- Deterministic Encryption
- Homomorphic Encryption
- Searchable Symmetric Encryption (SSE)
- You Can Have Little a HMAC, As a Treat
- Intermission
- Case Study: MongoDB Client-Side Encryption
- Wrapping Up
Database Cryptography?
The premise of database cryptography is deceptively simple: You have a database, of some sort, and you want to store sensitive data in said database.
The consequences of this simple premise are anything but simple. Let me explain.

The sensitive data you want to store may need to remain confidential, or you may need to provide some sort of integrity guarantees throughout your entire system, or sometimes both. Sometimes all of your data is sensitive, sometimes only some of it is. Sometimes the confidentiality requirements of your data extends to where within a dataset the record you want actually lives. Sometimes that’s true of some data, but not others, so your cryptography has to be flexible to support multiple types of workloads.
Other times, you just want your disks encrypted at rest so if they grow legs and walk out of the data center, the data cannot be comprehended by an attacker. And you can’t be bothered to work on this problem any deeper. This is usually what compliance requirements cover. Boxes get checked, executives feel safer about their operation, and the whole time nobody has really analyzed the risks they’re facing.
But we’re not settling for mere compliance on this blog. Furries have standards, after all.
So the first thing you need to do before diving into database cryptography is threat modelling. The first step in any good threat model is taking inventory; especially of assumptions, requirements, and desired outcomes. A few good starter questions:
- What database software is being used? Is it up to date?
- What data is being stored in which database software?
- How are databases oriented in the network of the overall system?
- Is your database properly firewalled from the public Internet?
- How does data flow throughout the network, and when do these data flows intersect with the database?
- Which applications talk to the database? What languages are they written in? Which APIs do they use?
- How will cryptography secrets be managed?
- Is there one key for everyone, one key per tenant, etc.?
- How are keys rotated?
- Do you use envelope encryption with an HSM, or vend the raw materials to your end devices?
The first two questions are paramount for deciding how to write software for database cryptography, before you even get to thinking about the cryptography itself.
(This is not a comprehensive set of questions to ask, either. A formal threat model is much deeper in the weeds.)
The kind of cryptography protocol you need for, say, storing encrypted CSV files an S3 bucket is vastly different from relational (SQL) databases, which in turn will be significantly different from schema-free (NoSQL) databases.
Furthermore, when you get to the point that you can start to think about the cryptography, you’ll often need to tackle confidentiality and integrity separately.
If that’s unclear, think of a scenario like, “I need to encrypt PII, but I also need to digitally sign the lab results so I know it wasn’t tampered with at rest.”
My point is, right off the bat, we’ve got a three-dimensional matrix of complexity to contend with:
- On one axis, we have the type of database.
- Flat-file
- Relational
- Schema-free
- On another, we have the basic confidentiality requirements of the data.
- Field encryption
- Row encryption
- Column encryption
- Unstructured record encryption
- Encrypting entire collections of records
- Finally, we have the integrity requirements of the data.
- Field authentication
- Row/column authentication
- Unstructured record authentication
- Collection authentication (based on e.g. Sparse Merkle Trees)
And then you have a fourth dimension that often falls out of operational requirements for databases: Searchability.
Why store data in a database if you have no way to index or search the data for fast retrieval?

If you’re starting to feel overwhelmed, you’re not alone. A lot of developers drastically underestimate the difficulty of the undertaking, until they run head-first into the complexity.
Some just phone it in with AES_Encrypt() calls in their MySQL queries. (Too bad ECB mode doesn’t provide semantic security!)
Which brings us to the meat of this blog post: The actual cryptography part.
Cryptography is the art of transforming information security problems into key management problems.Former coworker
Note: In the interest of time, I’m skipping over flat files and focusing instead on actual database technologies.
Cryptography for Relational Databases
Encrypting data in an SQL database seems simple enough, even if you’ve managed to shake off the complexity I teased from the introduction.
You’ve got data, you’ve got a column on a table. Just encrypt the data and shove it in a cell on that column and call it a day, right?
But, alas, this is a trap. There are so many gotchas that I can’t weave a coherent, easy-to-follow narrative between them all.
So let’s start with a simple question: where and how are you performing your encryption?
The Perils of Built-in Encryption Functions
MySQL provides functions called AES_Encrypt and AES_Decrypt, which many developers have unfortunately decided to rely on in the past.
It’s unfortunate because these functions implement ECB mode. To illustrate why ECB mode is bad, I encrypted one of my art commissions with AES in ECB mode:

The problems with ECB mode aren’t exactly “you can see the image through it,” because ECB-encrypting a compressed image won’t have redundancy (and thus can make you feel safer than you are).
ECB art is a good visual for the actual issue you should care about, however: A lack of semantic security.
A cryptosystem is considered semantically secure if observing the ciphertext doesn’t reveal information about the plaintext (except, perhaps, the length; which all cryptosystems leak to some extent). More information here.
ECB art isn’t to be confused with ECB poetry, which looks like this:
Oh little one, you’re growing up
You’ll soon be writing C
You’ll treat your ints as pointers
You’ll nest the ternary
You’ll cut and paste from github
And try cryptography
But even in your darkest hour
Do not use ECBCBC’s BEASTly when padding’s abused
And CTR’s fine til a nonce is reused
Some say it’s a CRIME to compress then encrypt
Or store keys in the browser (or use javascript)
Diffie Hellman will collapse if hackers choose your g
And RSA is full of traps when e is set to 3
Whiten! Blind! In constant time! Don’t write an RNG!
But failing all, and listen well: Do not use ECBThey’ll say “It’s like a one-time-pad!
The data’s short, it’s not so bad
the keys are long–they’re iron clad
I have a PhD!”
And then you’re front page Hacker News
Your passwords cracked–Adobe Blues.
Don’t leave your penguins showing through,
Do not use ECB— Ben Nagy, PoC||GTFO 0x04:13
Most people reading this probably know better than to use ECB mode already, and don’t need any of these reminders, but there is still a lot of code that inadvertently uses ECB mode to encrypt data in the database.
Also, SHOW processlist; leaks your encryption keys. Oops.

Application-layer Relational Database Cryptography
Whether burned by ECB or just cautious about not giving your secrets to the system that stores all the ciphertext protected by said secret, a common next step for developers is to simply encrypt in their server-side application code.
And, yes, that’s part of the answer. But how you encrypt is important.

“I’ll encrypt with CBC mode.”
If you don’t authenticate your ciphertext, you’ll be sorry. Maybe try again?
“Okay, fine, I’ll use an authenticated mode like GCM.”
Did you remember to make the table and column name part of your AAD? What about the primary key of the record?
“What on Earth are you talking about, Soatok?”
Welcome to the first footgun of database cryptography!
Confused Deputies
Encrypting your sensitive data is necessary, but not sufficient. You need to also bind your ciphertexts to the specific context in which they are stored.
To understand why, let’s take a step back: What specific threat does encrypting your database records protect against?
We’ve already established that “your disks walk out of the datacenter” is a “full disk encryption” problem, so if you’re using application-layer cryptography to encrypt data in a relational database, your threat model probably involves unauthorized access to the database server.
What, then, stops an attacker from copying ciphertexts around?

Let’s say I have a legitimate user account with an ID 12345, and I want to read your street address, but it’s encrypted in the database. But because I’m a clever hacker, I have unfettered access to your relational database server.
All I would need to do is simply…
UPDATE table SET addr_encrypted = 'your-ciphertext' WHERE id = 12345
…and then access the application through my legitimate access. Bam, data leaked. As an attacker, I can probably even copy fields from other columns and it will just decrypt. Even if you’re using an authenticated mode.
We call this a confused deputy attack, because the deputy (the component of the system that has been delegated some authority or privilege) has become confused by the attacker, and thus undermined an intended security goal.
The fix is to use the AAD parameter from the authenticated mode to bind the data to a given context. (AAD = Additional Authenticated Data.)
- $addr = aes_gcm_encrypt($addr, $key);+ $addr = aes_gcm_encrypt($addr, $key, canonicalize([+ $tableName,+ $columnName,+ $primaryKey+ ]);
Now if I start cutting and pasting ciphertexts around, I get a decryption failure instead of silently decrypting plaintext.
This may sound like a specific vulnerability, but it’s more of a failure to understand an important general lesson with database cryptography:
Where your data lives is part of its identity, and MUST be authenticated.Soatok’s Rule of Database Cryptography
Canonicalization Attacks
In the previous section, I introduced a pseudocode called canonicalize(). This isn’t a pasto from some reference code; it’s an important design detail that I will elaborate on now.
First, consider you didn’t do anything to canonicalize your data, and you just joined strings together and called it a day…
function dumbCanonicalize( string $tableName, string $columnName, string|int $primaryKey): string { return $tableName . '_' . $columnName . '#' . $primaryKey;}
Consider these two inputs to this function:
dumbCanonicalize('customers', 'last_order_uuid', 123);dumbCanonicalize('customers_last_order', 'uuid', 123);
In this case, your AAD would be the same, and therefore, your deputy can still be confused (albeit in a narrower use case).
In Cendyne’s article, AnonCo did something more subtle: The canonicalization bug created a collision on the inputs to HKDF, which resulted in an unintentional key reuse.
Up until this point, their mistake isn’t relevant to us, because we haven’t even explored key management at all. But the same design flaw can re-emerge in multiple locations, with drastically different consequence.
Multi-Tenancy
Once you’ve implemented a mitigation against Confused Deputies, you may think your job is done. And it very well could be.
Often times, however, software developers are tasked with building support for Bring Your Own Key (BYOK).
This is often spawned from a specific compliance requirement (such as cryptographic shredding; i.e. if you erase the key, you can no longer recover the plaintext, so it may as well be deleted).
Other times, this is driven by a need to cut costs: Storing different users’ data in the same database server, but encrypting it such that they can only encrypt their own records.
Two things can happen when you introduce multi-tenancy into your database cryptography designs:
- Invisible Salamanders becomes a risk, due to multiple keys being possible for any given encrypted record.
- Failure to address the risk of Invisible Salamanders can undermine your protection against Confused Deputies, thereby returning you to a state before you properly used the AAD.
So now you have to revisit your designs and ensure you’re using a key-committing authenticated mode, rather than just a regular authenticated mode.
Isn’t cryptography fun?
“What Are Invisible Salamanders?”
This refers to a fun property of AEAD modes based on Polynomical MACs. Basically, if you:
- Encrypt one message under a specific key and nonce.
- Encrypt another message under a separate key and nonce.
…Then you can get the same exact ciphertext and authentication tag. Performing this attack requires you to control the keys for both encryption operations.
This was first demonstrated in an attack against encrypted messaging applications, where a picture of a salamander was hidden from the abuse reporting feature because another attached file had the same authentication tag and ciphertext, and you could trick the system if you disclosed the second key instead of the first. Thus, the salamander is invisible to attackers.

We’re not quite done with relational databases yet, but we should talk about NoSQL databases for a bit. The final topic in scope applies equally to both, after all.
Cryptography for NoSQL Databases
Most of the topics from relational databases also apply to NoSQL databases, so I shall refrain from duplicating them here. This article is already sufficiently long to read, after all, and I dislike redundancy.
NoSQL is Built Different
The main thing that NoSQL databases offer in the service of making cryptographers lose sleep at night is the schema-free nature of NoSQL designs.
What this means is that, if you’re using a client-side encryption library for a NoSQL database, the previous concerns about confused deputy attacks are amplified by the malleability of the document structure.
Additionally, the previously discussed cryptographic attacks against the encryption mode may be less expensive for an attacker to pull off.
Consider the following record structure, which stores a bunch of data stored with AES in CBC mode:
{ "encrypted-data-key": "<blob>", "name": "<ciphertext>", "address": [ "<ciphertext>", "<ciphertext>" ], "social-security": "<ciphertext>", "zip-code": "<ciphertext>"}
If this record is decrypted with code that looks something like this:
$decrypted = [];// ... snip ...foreach ($record['address'] as $i => $addrLine) { try { $decrypted['address'][$i] = $this->decrypt($addrLine); } catch (Throwable $ex) { // You'd never deliberately do this, but it's for illustration $this->doSomethingAnOracleCanObserve($i); // This is more believable, of course: $this->logDecryptionError($ex, $addrLine); $decrypted['address'][$i] = ''; }}
Then you can keep appending rows to the "address" field to reduce the number of writes needed to exploit a padding oracle attack against any of the <ciphertext> fields.

This isn’t to say that NoSQL is less secure than SQL, from the context of client-side encryption. However, the powerful feature sets that NoSQL users are accustomed to may also give attackers a more versatile toolkit to work with.
Record Authentication
A pedant may point out that record authentication applies to both SQL and NoSQL. However, I mostly only observe this feature in NoSQL databases and document storage systems in the wild, so I’m shoving it in here.
Encrypting fields is nice and all, but sometimes what you want to know is that your unencrypted data hasn’t been tampered with as it flows through your system.
The trivial way this is done is by using a digital signature algorithm over the whole record, and then appending the signature to the end. When you go to verify the record, all of the information you need is right there.
This works well enough for most use cases, and everyone can pack up and go home. Nothing more to see here.
Except…
When you’re working with NoSQL databases, you often want systems to be able to write to additional fields, and since you’re working with schema-free blobs of data rather than a normalized set of relatable tables, the most sensible thing to do is to is to append this data to the same record.
Except, oops! You can’t do that if you’re shoving a digital signature over the record. So now you need to specify which fields are to be included in the signature.
And you need to think about how to model that in a way that doesn’t prohibit schema upgrades nor allow attackers to perform downgrade attacks. (See below.)

Art: CMYKat
Furthermore, as with preventing confused deputy and/or canonicalization attacks above, you must also include the fully qualified path of each field in the data that gets signed.
As I said with encryption before, but also true here:
Where your data lives is part of its identity, and MUST be authenticated.Soatok’s Rule of Database Cryptography
This requirement holds true whether you’re using symmetric-key authentication (i.e. HMAC) or asymmetric-key digital signatures (e.g. EdDSA).
Bonus: A Maximally Schema-Free, Upgradeable Authentication Design

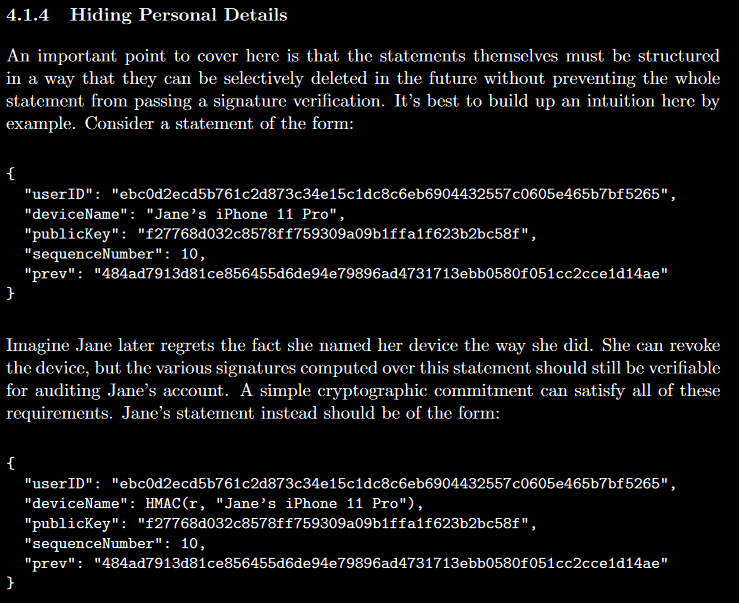
Okay, how do you solve this problem so that you can perform updates and upgrades to your schema but without enabling attackers to downgrade the security? Here’s one possible design.
Let’s say you have two metadata fields on each record:
- A compressed binary string representing which fields should be authenticated. This field is, itself, not authenticated. Let’s call this
meta-auth. - A compressed binary string representing which of the authenticated fields should also be encrypted. This field is also authenticated. This is at most the same length as the first metadata field. Let’s call this
meta-enc.
Furthermore, you will specify a canonical field ordering for both how data is fed into the signature algorithm as well as the field mappings in meta-auth and meta-enc.
{ "example": { "credit-card": { "number": /* encrypted */, "expiration": /* encrypted */, "ccv": /* encrypted */ }, "superfluous": { "rewards-member": null } }, "meta-auth": compress_bools([ true, /* example.credit-card.number */ true, /* example.credit-card.expiration */ true, /* example.credit-card.ccv */ false, /* example.superfluous.rewards-member */ true /* meta-enc */ ]), "meta-enc": compress_bools([ true, /* example.credit-card.number */ true, /* example.credit-card.expiration */ true, /* example.credit-card.ccv */ false /* example.superfluous.rewards-member */ ]), "signature": /* -- snip -- */}
When you go to append data to an existing record, you’ll need to update meta-auth to include the mapping of fields based on this canonical ordering to ensure only the intended fields get validated.
When you update your code to add an additional field that is intended to be signed, you can roll that out for new records and the record will continue to be self-describing:
- New records will have the additional field flagged as authenticated in
meta-auth(andmeta-encwill grow) - Old records will not, but your code will still sign them successfully
- To prevent downgrade attacks, simply include a schema version ID as an additional plaintext field that gets authenticated. An attacker who tries to downgrade will need to be able to produce a valid signature too.
You might think meta-auth gives an attacker some advantage, but this only includes which fields are included in the security boundary of the signature or MAC, which allows unauthenticated data to be appended for whatever operational purpose without having to update signatures or expose signing keys to a wider part of the network.
{ "example": { "credit-card": { "number": /* encrypted */, "expiration": /* encrypted */, "ccv": /* encrypted */ }, "superfluous": { "rewards-member": null } }, "meta-auth": compress_bools([ true, /* example.credit-card.number */ true, /* example.credit-card.expiration */ true, /* example.credit-card.ccv */ false, /* example.superfluous.rewards-member */ true, /* meta-enc */ true /* meta-version */ ]), "meta-enc": compress_bools([ true, /* example.credit-card.number */ true, /* example.credit-card.expiration */ true, /* example.credit-card.ccv */ false, /* example.superfluous.rewards-member */ true /* meta-version */ ]), "meta-version": 0x01000000, "signature": /* -- snip -- */}
If an attacker tries to use the meta-auth field to mess with a record, the best they can hope for is an Invalid Signature exception (assuming the signature algorithm is secure to begin with).
Even if they keep all of the fields the same, but play around with the structure of the record (e.g. changing the XPath or equivalent), so long as the path is authenticated with each field, breaking this is computationally infeasible.
Searchable Encryption
If you’ve managed to make it through the previous sections, congratulations, you now know enough to build a secure but completely useless database.

Okay, put away the pitchforks; I will explain.
Part of the reason why we store data in a database, rather than a flat file, is because we want to do more than just read and write. Sometimes computer scientists want to compute. Almost always, you want to be able to query your database for a subset of records based on your specific business logic needs.
And so, a database which doesn’t do anything more than store ciphertext and maybe signatures is pretty useless to most people. You’d have better luck selling Monkey JPEGs to furries than convincing most businesses to part with their precious database-driven report generators.

So whenever one of your users wants to actually use their data, rather than just store it, they’re forced to decide between two mutually exclusive options:
- Encrypting the data, to protect it from unauthorized disclosure, but render it useless
- Doing anything useful with the data, but leaving it unencrypted in the database
This is especially annoying for business types that are all in on the Zero Trust buzzword.
Fortunately, the cryptographers are at it again, and boy howdy do they have a lot of solutions for this problem.
Order-{Preserving, Revealing} Encryption
On the fun side of things, you have things like Order-Preserving and Order-Revealing Encryption, which Matthew Green wrote about at length.
[D]atabase encryption has been a controversial subject in our field. I wish I could say that there’s been an actual debate, but it’s more that different researchers have fallen into different camps, and nobody has really had the data to make their position in a compelling way. There have actually been some very personal arguments made about it.Attack of the week: searchable encryption and the ever-expanding leakage function
The problem with these designs is that they have a significant enough leakage that it no longer provides semantic security.
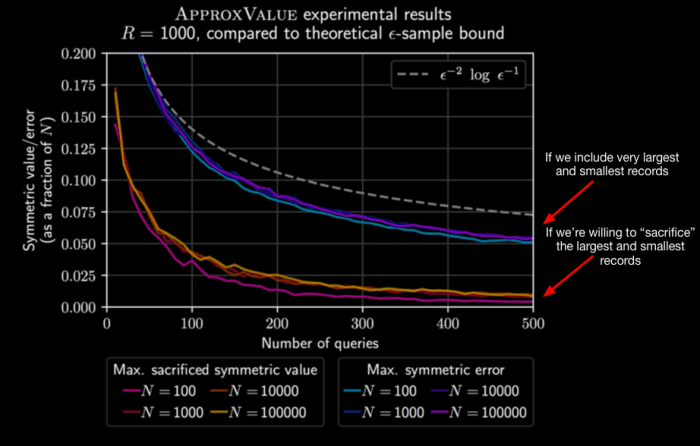
Colors inverted to fit my blog’s theme better.
To put it in other words: These designs are only marginally better than ECB mode, and probably deserve their own poems too.
Order revealing
Reveals much more than order
Softcore ECBOrder preserving
Semantic security?
Only in your dreamsHaiku for your consideration
Deterministic Encryption
Here’s a simpler, but also terrible, idea for searchable encryption: Simply give up on semantic security entirely.
If you recall the AES_{De,En}crypt() functions built into MySQL I mentioned at the start of this article, those are the most common form of deterministic encryption I’ve seen in use.
SELECT * FROM foo WHERE bar = AES_Encrypt('query', 'key');
However, there are slightly less bad variants. If you use AES-GCM-SIV with a static nonce, your ciphertexts are fully deterministic, and you can encrypt a small number of distinct records safely before you’re no longer secure.
That’s certainly better than nothing, but you also can’t mitigate confused deputy attacks. But we can do better than this.
Homomorphic Encryption
In a safer plane of academia, you’ll find homomorphic encryption, which researchers recently demonstrated with serving Wikipedia pages in a reasonable amount of time.
Homomorphic encryption allows computations over the ciphertext, which will be reflected in the plaintext, without ever revealing the key to the entity performing the computation.
If this sounds vaguely similar to the conditions that enable chosen-ciphertext attacks, you probably have a good intuition for how it works: RSA is homomorphic to multiplication, AES-CTR is homomorphic to XOR. Fully homomorphic encryption uses lattices, which enables multiple operations but carries a relatively enormous performance cost.

Homomorphic encryption sometimes intersects with machine learning, because the notion of training an encrypted model by feeding it encrypted data, then decrypting it after-the-fact is desirable for certain business verticals. Your data scientists never see your data, and you have some plausible deniability about the final ML model this work produces. This is like a Siren song for Venture Capitalist-backed medical technology companies. Tech journalists love writing about it.
However, a less-explored use case is the ability to encrypt your programs but still get the correct behavior and outputs. Although this sounds like a DRM technology, it’s actually something that individuals could one day use to prevent their ISPs or cloud providers from knowing what software is being executed on the customer’s leased hardware. The potential for a privacy win here is certainly worth pondering, even if you’re a tried and true Pirate Party member.

Art: CMYKat
Searchable Symmetric Encryption (SSE)
Forget about working at the level of fields and rows or individual records. What if we, instead, worked over collections of documents, where each document is viewed as a set of keywords from a keyword space?

That’s the basic premise of SSE: Encrypting collections of documents rather than individual records.
The actual implementation details differ greatly between designs. They also differ greatly in their leakage profiles and susceptibility to side-channel attacks.
Some schemes use a so-called trapdoor permutation, such as RSA, as one of their building blocks.
Some schemes only allow for searching a static set of records, while others can accommodate new data over time (with the trade-off between more leakage or worse performance).
If you’re curious, you can learn more about SSE here, and see some open source SEE implementations online here.
You’re probably wondering, “If SSE is this well-studied and there are open source implementations available, why isn’t it more widely used?”
Your guess is as good as mine, but I can think of a few reasons:
- The protocols can be a little complicated to implement, and aren’t shipped by default in cryptography libraries (i.e. OpenSSL’s libcrypto or libsodium).
- Every known security risk in SSE is the product of a trade-offs, rather than there being a single winner for all use cases that developers can feel comfortable picking.
- Insufficient marketing and developer advocacy.
SSE schemes are mostly of interest to academics, although Seny Kamara (Brown Univeristy professior and one of the luminaries of searchable encryption) did try to develop an app called Pixek which used SSE to encrypt photos.
Maybe there’s room for a cryptography competition on searchable encryption schemes in the future.
You Can Have Little a HMAC, As a Treat
Finally, I can’t talk about searchable encryption without discussing a technique that’s older than dirt by Internet standards, that has been independently reinvented by countless software developers tasked with encrypting database records.
The oldest version I’ve been able to track down dates to 2006 by Raul Garcia at Microsoft, but I’m not confident that it didn’t exist before.
The idea I’m alluding to goes like this:
- Encrypt your data, securely, using symmetric cryptography.
(Hopefully your encryption addresses the considerations outlined in the relevant sections above.) - Separately, calculate an HMAC over the unencrypted data with a separate key used exclusively for indexing.
When you need to query your data, you can just recalculate the HMAC of your challenge and fetch the records that match it. Easy, right?
Even if you rotate your keys for encryption, you keep your indexing keys static across your entire data set. This lets you have durable indexes for encrypted data, which gives you the ability to do literal lookups for the performance hit of a hash function.
Additionally, everyone has HMAC in their toolkit, so you don’t have to move around implementations of complex cryptographic building blocks. You can live off the land. What’s not to love?

However, if you stopped here, we regret to inform you that your data is no longer indistinguishable from random, which probably undermines the security proof for your encryption scheme.

Of course, you don’t have to stop with the addition of plain HMAC to your database encryption software.
Take a page from Troy Hunt: Truncate the output to provide k-anonymity rather than a direct literal look-up.
“K-What Now?”
Imagine you have a full HMAC-SHA256 of the plaintext next to every ciphertext record with a static key, for searchability.
Each HMAC output corresponds 1:1 with a unique plaintext.
Because you’re using HMAC with a secret key, an attacker can’t just build a rainbow table like they would when attempting password cracking, but it still leaks duplicate plaintexts.
For example, an HMAC-SHA256 output might look like this: 04a74e4c0158e34a566785d1a5e1167c4e3455c42aea173104e48ca810a8b1ae

If you were to slice off most of those bytes (e.g. leaving only the last 3, which in the previous example yields a8b1ae), then with sufficient records, multiple plaintexts will now map to the same truncated HMAC tag.
Which means if you’re only revealing a truncated HMAC tag to the database server (both when storing records or retrieving them), you can now expect false positives due to collisions in your truncated HMAC tag.
These false positives give your data a discrete set of anonymity (called k-anonymity), which means an attacker with access to your database cannot:
- Distinguish between two encrypted records with the same short HMAC tag.
- Reverse engineer the short HMAC tag into a single possible plaintext value, even if they can supply candidate queries and study the tags sent to the database.

As with SSE above, this short HMAC technique exposes a trade-off to users.
- Too much k-anonymity (i.e. too many false positives), and you will have to decrypt-then-discard multiple mismatching records. This can make queries slow.
- Not enough k-anonymity (i.e. insufficient false positives), and you’re no better off than a full HMAC.
Even more troublesome, the right amount to truncate is expressed in bits (not bytes), and calculating this value depends on the number of unique plaintext values you anticipate in your dataset. (Fortunately, it grows logarithmically, so you’ll rarely if ever have to tune this.)
If you’d like to play with this idea, here’s a quick and dirty demo script.
Intermission
If you started reading this post with any doubts about Cendyne’s statement that “Database cryptography is hard”, by making it to this point, they’ve probably been long since put to rest.

Conversely, anyone that specializes in this topic is probably waiting for me to say anything novel or interesting; their patience wearing thin as I continue to rehash a surface-level introduction of their field without really diving deep into anything.
Thus, if you’ve read this far, I’d like to demonstrate the application of what I’ve covered thus far into a real-world case study into an database cryptography product.
Case Study: MongoDB Client-Side Encryption
MongoDB is an open source schema-free NoSQL database. Last year, MongoDB made waves when they announced Queryable Encryption in their upcoming client-side encryption release.
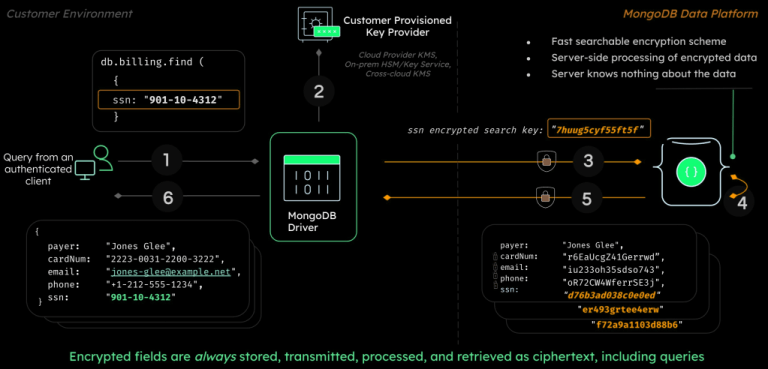
A statement at the bottom of their press release indicates that this isn’t clown-shoes:
Queryable Encryption was designed by MongoDB’s Advanced Cryptography Research Group, headed by Seny Kamara and Tarik Moataz, who are pioneers in the field of encrypted search. The Group conducts cutting-edge peer-reviewed research in cryptography and works with MongoDB engineering teams to transfer and deploy the latest innovations in cryptography and privacy to the MongoDB data platform.
If you recall, I mentioned Seny Kamara in the SSE section of this post. They certainly aren’t wrong about Kamara and Moataz being pioneers in this field.
So with that in mind, let’s explore the implementation in libmongocrypt and see how it stands up to scrutiny.
MongoCrypt: The Good
MongoDB’s encryption library takes key management seriously: They provide a KMS integration for cloud users by default (supporting both AWS and Azure).
MongoDB uses Encrypt-then-MAC with AES-CBC and HMAC-SHA256, which is congruent to what Signal does for message encryption.
How Is Queryable Encryption Implemented?
From the current source code, we can see that MongoCrypt generates several different types of tokens, using HMAC (calculation defined here).
According to their press release:
The feature supports equality searches, with additional query types such as range, prefix, suffix, and substring planned for future releases.
Which means that most of the juicy details probably aren’t public yet.
These HMAC-derived tokens are stored wholesale in the data structure, but most are encrypted before storage using AES-CTR.
There are more layers of encryption (using AEAD), server-side token processing, and more AES-CTR-encrypted edge tokens. All of this is finally serialized (implementation) as one blob for storage.
Since only the equality operation is currently supported (which is the same feature you’d get from HMAC), it’s difficult to speculate what the full feature set looks like.
However, since Kamara and Moataz are leading its development, it’s likely that this feature set will be excellent.
MongoCrypt: The Bad
Every call to do_encrypt() includes at most the Key ID (but typically NULL) as the AAD. This means that the concerns over Confused Deputies (and NoSQL specifically) are relevant to MongoDB.
However, even if they did support authenticating the fully qualified path to a field in the AAD for their encryption, their AEAD construction is vulnerable to the kind of canonicalization attack I wrote about previously.
First, observe this code which assembles the multi-part inputs into HMAC.
/* Construct the input to the HMAC */uint32_t num_intermediates = 0;_mongocrypt_buffer_t intermediates[3];// -- snip --if (!_mongocrypt_buffer_concat ( &to_hmac, intermediates, num_intermediates)) { CLIENT_ERR ("failed to allocate buffer"); goto done;}if (hmac == HMAC_SHA_512_256) { uint8_t storage[64]; _mongocrypt_buffer_t tag = {.data = storage, .len = sizeof (storage)}; if (!_crypto_hmac_sha_512 (crypto, Km, &to_hmac, &tag, status)) { goto done; } // Truncate sha512 to first 256 bits. memcpy (out->data, tag.data, MONGOCRYPT_HMAC_LEN);} else { BSON_ASSERT (hmac == HMAC_SHA_256); if (!_mongocrypt_hmac_sha_256 (crypto, Km, &to_hmac, out, status)) { goto done; }}
The implementation of _mongocrypt_buffer_concat() can be found here.
If either the implementation of that function, or the code I snipped from my excerpt, had contained code that prefixed every segment of the AAD with the length of the segment (represented as a uint64_t to make overflow infeasible), then their AEAD mode would not be vulnerable to canonicalization issues.
Using TupleHash would also have prevented this issue.
Silver lining for MongoDB developers: Because the AAD is either a key ID or NULL, this isn’t exploitable in practice.
The first cryptographic flaw sort of cancels the second out.
If the libmongocrypt developers ever want to mitigate Confused Deputy attacks, they’ll need to address this canonicalization issue too.
MongoCrypt: The Ugly
MongoCrypt supports deterministic encryption.
If you specify deterministic encryption for a field, your application passes a deterministic initialization vector to AEAD.
We already discussed why this is bad above.
Wrapping Up
This was not a comprehensive treatment of the field of database cryptography. There are many areas of this field that I did not cover, nor do I feel qualified to discuss.
However, I hope anyone who takes the time to read this finds themselves more familiar with the subject.
Additionally, I hope any developers who think “encrypting data in a database is [easy, trivial] (select appropriate)” will find this broad introduction a humbling experience.

https://soatok.blog/2023/03/01/database-cryptography-fur-the-rest-of-us/
#appliedCryptography #blockCipherModes #cryptography #databaseCryptography #databases #encryptedSearch #HMAC #MongoCrypt #MongoDB #QueryableEncryption #realWorldCryptography #security #SecurityGuidance #SQL #SSE #symmetricCryptography #symmetricSearchableEncryption
NIST opened public comments on SP 800-108 Rev. 1 (the NIST recommendations for Key Derivation Functions) last month. The main thing that’s changed from the original document published in 2009 is the inclusion of the Keccak-based KMAC alongside the incumbent algorithms.One of the recommendations of SP 800-108 is called “KDF in Counter Mode”. A related document, SP 800-56C, suggests using a specific algorithm called HKDF instead of the generic Counter Mode construction from SP 800-108–even though they both accomplish the same goal.
Isn’t standards compliance fun?
Interestingly, HKDF isn’t just an inconsistently NIST-recommended KDF, it’s also a common building block in a software developer’s toolkit which sees a lot of use in different protocols.
Unfortunately, the way HKDF is widely used is actually incorrect given its formal security definition. I’ll explain what I mean in a moment.
Art: Scruff
What is HKDF?
To first understand what HKDF is, you first need to know about HMAC.HMAC is a standard message authentication code (MAC) algorithm built with cryptographic hash functions (that’s the H). HMAC is specified in RFC 2104 (yes, it’s that old).
HKDF is a key-derivation function that uses HMAC under-the-hood. HKDF is commonly used in encryption tools (Signal, age). HKDF is specified in RFC 5869.
HKDF is used to derive a uniformly-random secret key, typically for use with symmetric cryptography algorithms. In any situation where a key might need to be derived, you might see HKDF being used. (Although, there may be better algorithms.)
Art: LvJ
How Developers Understand and Use HKDF
If you’re a software developer working with cryptography, you’ve probably seen an API in the crypto module for your programming language that looks like this, or maybe this.hash_hkdf( string $algo, string $key, int $length = 0, string $info = "", string $salt = ""): string
Software developers that work with cryptography will typically think of the HKDF parameters like so:
$algo— which hash function to use$key— the input key, from which multiple keys can be derived$length— how many bytes to derive$info— some arbitrary string used to bind a derived key to an intended context$salt— some additional randomness (optional)The most common use-case of HKDF is to implement key-splitting, where a single input key (the Initial Keying Material, or IKM) is used to derive two or more independent keys, so that you’re never using a single key for multiple algorithms.
See also:
[url=https://github.com/defuse/php-encryption]defuse/php-encryption[/url], a popular PHP encryption library that does exactly what I just described.At a super high level, the HKDF usage I’m describing looks like this:
class MyEncryptor {protected function splitKeys(CryptographyKey $key, string $salt): array { $encryptKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, 'encryption', $salt )); $authKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, 'message authentication', $salt )); return [$encryptKey, $authKey];}public function encryptString(string $plaintext, CryptographyKey $key): string{ $salt = random_bytes(32); [$encryptKey, $hmacKey] = $this->splitKeys($key, $salt); // ... encryption logic here ... return base64_encode($salt . $ciphertext . $mac);}public function decryptString(string $encrypted, CryptographyKey $key): string{ $decoded = base64_decode($encrypted); $salt = mb_substr($decoded, 0, 32, '8bit'); [$encryptKey, $hmacKey] = $this->splitKeys($key, $salt); // ... decryption logic here ... return $plaintext;}// ... other method here ...}
Unfortunately, anyone who ever does something like this just violated one of the core assumptions of the HKDF security definition and no longer gets to claim “KDF security” for their construction. Instead, your protocol merely gets to claim “PRF security”.
Art: Harubaki
KDF? PRF? OMGWTFBBQ?
Let’s take a step back and look at some basic concepts.(If you want a more formal treatment, read this Stack Exchange answer.)
PRF: Pseudo-Random Functions
A pseudorandom function (PRF) is an efficient function that emulates a random oracle.“What the hell’s a random oracle?” you ask? Well, Thomas Pornin has the best explanation for random oracles:
A random oracle is described by the following model:
- There is a black box. In the box lives a gnome, with a big book and some dice.
- We can input some data into the box (an arbitrary sequence of bits).
- Given some input that he did not see beforehand, the gnome uses his dice to generate a new output, uniformly and randomly, in some conventional space (the space of oracle outputs). The gnome also writes down the input and the newly generated output in his book.
- If given an already seen input, the gnome uses his book to recover the output he returned the last time, and returns it again.
So a random oracle is like a kind of hash function, such that we know nothing about the output we could get for a given input message m. This is a useful tool for security proofs because they allow to express the attack effort in terms of number of invocations to the oracle.
The problem with random oracles is that it turns out to be very difficult to build a really “random” oracle. First, there is no proof that a random oracle can really exist without using a gnome. Then, we can look at what we have as candidates: hash functions. A secure hash function is meant to be resilient to collisions, preimages and second preimages. These properties do not imply that the function is a random oracle.
Thomas Pornin
Alternatively, Wikipedia has a more formal definition available to the academic-inclined.In practical terms, we can generate a strong PRF out of secure cryptographic hash functions by using a keyed construction; i.e. HMAC.
Thus, as long as your HMAC key is a secret, the output of HMAC can be generally treated as a PRF for all practical purposes. Your main security consideration (besides key management) is the collision risk if you truncate its output.
Art: LvJ
KDF: Key Derivation Functions
A key derivation function (KDF) is exactly what it says on the label: a cryptographic algorithm that derives one or more cryptographic keys from a secret input (which may be another cryptography key, a group element from a Diffie-Hellman key exchange, or a human-memorable password).Note that passwords should be used with a Password-Based Key Derivation Function, such as scrypt or Argon2id, not HKDF.
Despite what you may read online, KDFs do not need to be built upon cryptographic hash functions, specifically; but in practice, they often are.
A notable counter-example to this hash function assumption: CMAC in Counter Mode (from NIST SP 800-108) uses AES-CMAC, which is a variable-length input variant of CBC-MAC. CBC-MAC uses a block cipher, not a hash function.
Regardless of the construction, KDFs use a PRF under the hood, and the output of a KDF is supposed to be a uniformly random bit string.
Art: LvJ
PRF vs KDF Security Definitions
The security definition for a KDF has more relaxed requirements than PRFs: PRFs require the secret key be uniformly random. KDFs do not have this requirement.If you use a KDF with a non-uniformly random IKM, you probably need the KDF security definition.
If your IKM is already uniformly random (i.e. the “key separation” use case), you can get by with just a PRF security definition.
After all, the entire point of KDFs is to allow a congruent security level as you’d get from uniformly random secret keys, without also requiring them.
However, if you’re building a protocol with a security requirement satisfied by a KDF, but you actually implemented a PRF (i.e., not a KDF), this is a security vulnerability in your cryptographic design.
Art: LvJ
The HKDF Algorithm
HKDF is an HMAC-based KDF. Its algorithm consists of two distinct steps:
HKDF-Extractuses the Initial Keying Material (IKM) and Salt to produce a Pseudo-Random Key (PRK).HKDF-Expandactually derives the keys using PRK, theinfoparameter, and a counter (from0to255) for each hash function output needed to generate the desired output length.If you’d like to see an implementation of this algorithm,
defuse/php-encryptionprovides one (since it didn’t land in PHP until 7.1.0). Alternatively, there’s a Python implementation on Wikipedia that uses HMAC-SHA256.This detail about the two steps will matter a lot in just a moment.
Art: Swizz
How HKDF Salts Are Misused
The HKDF paper, written by Hugo Krawczyk, contains the following definition (page 7).
The paper goes on to discuss the requirements for authenticating the salt over the communication channel, lest the attacker have the ability to influence it.
A subtle detail of this definition is that the security definition says that A salt value
, not Multiple salt values.
Which means: You’re not supposed to use HKDF with a constant IKM, info label, etc. but vary the salt for multiple invocations. The salt must either be a fixed random value, or NULL.
The HKDF RFC makes this distinction even less clear when it argues for random salts.
We stress, however, that the use of salt adds significantly to the strength of HKDF, ensuring independence between different uses of the hash function, supporting “source-independent” extraction, and strengthening the analytical results that back the HKDF design.Random salt differs fundamentally from the initial keying material in two ways: it is non-secret and can be re-used. As such, salt values are available to many applications. For example, a pseudorandom number generator (PRNG) that continuously produces outputs by applying HKDF to renewable pools of entropy (e.g., sampled system events) can fix a salt value and use it for multiple applications of HKDF without having to protect the secrecy of the salt. In a different application domain, a key agreement protocol deriving cryptographic keys from a Diffie-Hellman exchange can derive a salt value from public nonces exchanged and authenticated between communicating parties as part of the key agreement (this is the approach taken in [IKEv2]).
RFC 5869, section 3.1
Okay, sure. Random salts are better than a NULL salt. And while this section alludes to “[fixing] a salt value” to “use it for multiple applications of HKDF without having to protect the secrecy of the salt”, it never explicitly states this requirement. Thus, the poor implementor is left to figure this out on their own.Thus, because it’s not using HKDF in accordance with its security definition, many implementations (such as the PHP encryption library we’ve been studying) do not get to claim that their construction has KDF security.
Instead, they only get to claim “Strong PRF” security, which you can get from just using HMAC.
Art: LvJ
What Purpose Do HKDF Salts Actually Serve?
Recall that the HKDF algorithm uses salts in the HDKF-Extract step. Salts in this context were intended for deriving keys from a Diffie-Hellman output, or a human-memorable password.In the case of [Elliptic Curve] Diffie-Hellman outputs, the result of the key exchange algorithm is a random group element, but not necessarily uniformly random bit string. There’s some structure to the output of these functions. This is why you always, at minimum, apply a cryptographic hash function to the output of [EC]DH before using it as a symmetric key.
HKDF uses salts as a mechanism to improve the quality of randomness when working with group elements and passwords.
Extending the nonce for a symmetric-key AEAD mode is a good idea, but using HKDF’s salt parameter specifically to accomplish this is a misuse of its intended function, and produces a weaker argument for your protocol’s security than would otherwise be possible.
How Should You Introduce Randomness into HKDF?
Just shove it in theinfoparameter.
Art: LvJ
It may seem weird, and defy intuition, but the correct way to introduce randomness into HKDF as most developers interact with the algorithm is to skip the salt parameter entirely (either fixing it to a specific value for domain-separation or leaving it NULL), and instead concatenate data into the
infoparameter.class BetterEncryptor extends MyEncryptor {protected function splitKeys(CryptographyKey $key, string $salt): array { $encryptKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, $salt . 'encryption', '' // intentionally empty )); $authKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, $salt . 'message authentication', '' // intentionally empty )); return [$encryptKey, $authKey];}}
Of course, you still have to watch out for canonicalization attacks if you’re feeding multi-part messages into the info tag.
Another advantage: This also lets you optimize your HKDF calls by caching the PRK from the
HKDF-Extractstep and reuse it for multiple invocations ofHKDF-Expandwith a distinctinfo. This allows you to reduce the number of hash function invocations fromto
(since each HMAC involves two hash function invocations).
Notably, this HKDF salt usage was one of the things that was changed in V3/V4 of PASETO.
Does This Distinction Really Matter?
If it matters, your cryptographer will tell you it matters–which probably means they have a security proof that assumes the KDF security definition for a very good reason, and you’re not allowed to violate that assumption.Otherwise, probably not. Strong PRF security is still pretty damn good for most threat models.
Art: LvJ
Closing Thoughts
If your takeaway was, “Wow, I feel stupid,” don’t, because you’re in good company.I’ve encountered several designs in my professional life that shoved the randomness into the
infoparameter, and it perplexed me because there was a perfectly good salt parameter right there. It turned out, I was wrong to believe that, for all of the subtle and previously poorly documented reasons discussed above. But now we both know, and we’re all better off for it.So don’t feel dumb for not knowing. I didn’t either, until this was pointed out to me by a very patient colleague.
“Feeling like you were stupid” just means you learned.
(Art: LvJ)Also, someone should really get NIST to be consistent about whether you should use HKDF or “KDF in Counter Mode with HMAC” as a PRF, because SP 800-108’s new revision doesn’t concede this point at all (presumably a relic from the 2009 draft).
This concession was made separately in 2011 with SP 800-56C revision 1 (presumably in response to criticism from the 2010 HKDF paper), and the present inconsistency is somewhat vexing.
(On that note, does anyone actually use the NIST 800-108 KDFs instead of HKDF? If so, why? Please don’t say you need CMAC…)
Bonus Content
These questions were asked after this blog post initially went public, and I thought they were worth adding. If you ask a good question, it may end up being edited in at the end, too.
Art: LvJ
Why Does HKDF use the Salt as the HMAC key in the Extract Step? (via r/crypto)
Broadly speaking, when applying a PRF to two “keys”, you get to decide which one you treat as the “key” in the underlying API.HMAC’s API is HMACalg(key, message), but how HKDF uses it might as well be HMACalg(key1, key2).
The difference here seems almost arbitrary, but there’s a catch.
HKDF was designed for Diffie-Hellman outputs (before ECDH was the norm), which are generally able to be much larger than the block size of the underlying hash function. 2048-bit DH results fit in 256 bytes, which is 4 times the SHA256 block size.
If you have to make a decision, using the longer input (DH output) as the message is more intuitive for analysis than using it as the key, due to pre-hashing. I’ve discussed the counter-intuitive nature of HMAC’s pre-hashing behavior at length in this post, if you’re interested.
So with ECDH, it literally doesn’t matter which one was used (unless you have a weird mismatch in hash functions and ECC groups; i.e. NIST P-521 with SHA-224).
But before the era of ECDH, it was important to use the salt as the HMAC key in the extract step, since they were necessarily smaller than a DH group element.
Thus, HKDF chose HMACalg(salt, IKM) instead of HMACalg(IKM, salt) for the calculation of PRK in the HKDF-Extract step.
Neil Madden also adds that the reverse would create a chicken-egg situation, but I personally suspect that the pre-hashing would be more harmful to the security analysis than merely supplying a non-uniformly random bit string as an HMAC key in this specific context.
My reason for believing this is, when a salt isn’t supplied, it defaults to a string of
0x00bytes as long as the output size of the underlying hash function. If the uniform randomness of the salt mattered that much, this wouldn’t be a tolerable condition.https://soatok.blog/2021/11/17/understanding-hkdf/
#cryptographicHashFunction #cryptography #hashFunction #HMAC #KDF #keyDerivationFunction #securityDefinition #SecurityGuidance

Ever since the famous “Open Sesame” line from One Thousand and One Nights, humanity was doomed to suffer from the scourge of passwords.
Even in a world where we use hardware tokens with asymmetric cryptography to obviate the need for passwords in modern authentication protocols, we’ll still need to include “something you know” for legal and political reasons.
In the United States, we have the Fifth Amendment to the US Constitution, which prevents anyone from being forced to testify against oneself. This sometimes includes revealing a password, so it is imperative that passwords remain a necessary component of some encryption technologies to prevent prosecutors from side-stepping one’s Fifth Amendment rights. (Other countries have different laws about passwords. I’m not a lawyer.)
If you’ve ever read anything from the EFF, you’re probably keenly aware of this, but the US government loves to side-step citizens’ privacy rights in a court of law. They do this not out of direct malice towards civil rights (generally), but rather because it makes their job easier. Incentives rule everything around me.
Thus, even in a passwordless future, anyone who truly cares about civil liberties will not want to dispense with them entirely. Furthermore, we’ll want these password-based technologies to pass the Mud Puddle test, so that we aren’t relying on large tech companies to protect us from government backdoors.
Given all this, most security professionals will agree that passwords suck. Not only are humans bad sources of randomness, but we’re awful at memorizing a sequence of characters or words for every application, website, or operating system that demands a password.
None of what I’ve written so far is the least bit novel or interesting. But here’s a spicy take:
The only thing that sucks worse than passwords is the messaging around password-based cryptographic functions.
Password-Based Cryptographic Functions
That isn’t a term of the art, by the way. I’m kind of coining it as a superset that includes both Password-Based Key Derivation Functions and Password Hashing Functions.
You might be wondering, “Aren’t those two the same thing?” No, they are not. I will explain in a moment.
The intersection of human-memorable secrets (passwords) and cryptographic protocols manifests in a lot of needless complexity and edge-cases that, in order to sufficiently explain anything conversationally, will require me to sound either drunk or like a blue deck player in Magic: The Gathering.

Art: CMYKat
To that end, what I’m calling Password-Based Cryptographic Functions (PBCFs) includes all of the following:
- Password-Hashing Functions
- Bcrypt
- Password-Based Key Derivation Functions
- Scrypt
- Argon2
- PBKDF2
- bscrypt
- Balanced Password Authenticated Key Exchanges
- CPace
- Augmented Password Authenticated Key Exchanges
- SRP
- AuCPace
- BS-SPEKE
- Doubly-Augmented Password Authenticated Key Exchanges
- OPAQUE
- Double BS-SPEKE
If you tried to approach categorization starting with simply “Key Derivation Functions”, you’d quickly run into a problem: What about HKDF? Or any of the NIST SP 800-108 KDFs for that matter?
If you tighten it to “Password-Based KDFs” or “Key-stretching functions”, that doesn’t include bcrypt. Bcrypt is a password hashing function, but it’s not suitable for deriving secret keys. I’ve discussed these nuances previously.
And then you have some password KDF and/or hashing algorithms that are memory-hard, some that are cache-hard.
And then some Password Authenticated Key Exchanges (PAKEs) are quantum-annoying, while others are not.

To make heads or tails of the different algorithms, their properties, and when and where you should use them, you’d either need to secure postdoc funding for cryptography research or spend a lot of time reading and watching passwords-focused conference talks.

(Selfie taken by Sc00bz (left) at DEFCON 30 in the Quantum Village.)
So let’s talk about these different algorithms, why they exist to begin with, and some of their technical details.

Why Does Any of This Matter?
The intersection of passwords and cryptography is one of the foundations of modern society, and one that most Internet users experience everywhere they go.
You’ll know you have succeeded in designing a cryptographic algorithm when the best way to attack it is to try every possible key. This is called an exhaustive search, or a brute-force attack, depending on the disposition of the author.
Remember earlier when I said passwords suck because humans are bad at creating or remembering strong, unique passwords for every website they visit?
Well, it turns out, that some passwords are extremely common. And even worse, people who choose common passwords tend to reuse them everywhere.
This presented a challenge to early web applications: In order to have authenticated users, you need to collect a password from the user and check it on subsequent visits. If you ever get hacked, then it’s likely that all of your users will be impacted on other websites they used the same passwords for.
Including their bank accounts.
So the challenge for any password-based scheme is simply stated: How can you safely authenticate users based on a secret they know?
Enter: Hashing
Storing a hash of a password is an obvious solution to this predicament. Early solutions involved using the user’s password as an encryption key, rather than building atop cryptographic hash functions.
However, it’s important not to call it “password encryption”.
The reason isn’t merely pedantic; it’s meant to prevent a disaster from repeating: Adobe famously encrypted passwords with Triple-DES instead of hashing them.
In early UNIX-based operating systems, your password hashes were stored in a file called /etc/passwd, along with other user account data. These days, your actual password hashes are kept in a second file, /etc/shadow, which is only readable by root.
Unfortunately, the tool used to create password hashes was called crypt, so the “encryption” lingo stuck.

When Hashing Isn’t Enough
Although encrypting passwords is bad, using a fast cryptographic hash function (e.g. SHA256 or BLAKE2) is also bad.
LinkedIn learned this lesson the hard way in 2012, when an attacker leaked 117 million users’ hashed passwords. It turns out, they used SHA1 as their password hashing function.
Hash functions are deterministic: If you feed them the same input, you will always get the same output.
When your password hashing strategy is simply “just use SHA1”, two users with the same password will have an identical password hash.
People are bad at creating, or remembering, unpredictable passwords.
When you combine these observations, there are some extremely obvious candidates (123456, password, etc.) to prioritize when guessing.
Additionally, you could precompute these hashes once and build a reverse index of the passwords that hash to a specific output. This is called a rainbow table.
Unlike most of symmetric cryptography, where the goal ends at forcing the attacker to perform an exhaustive brute-force search of every possible key, password-based cryptography has to go the extra mile to prevent weak secrets from being compromised; a very tall order for anyone to contend with.
Towards Modern Password Hashing
None of this was a surprise to security experts in 2012. There were a couple generally known best practices since I first learned programming in the 2000s:
- Salt your passwords (to mitigate rainbow tables)
- Use an iterated hashing scheme, rather than a fast hash (to make each step of an exhaustive search slower)
PBKDF2, the first widely used password hashing and key derivation function, did exactly that:
- PBKDF2 was designed to support randomly-generated per-user salts.
- It used HMAC in a loop to force attackers to spend extra CPU cycles per guess. If an attacker could guess 10 million passwords per second against SHA-256, then using 100,000 iterations of PBKDF2 slowed them down to less than 100 guesses per second (due to HMAC calling the hash function twice).
And that might sound like the end of the story (“PBKDF2 wins”), but the password cracking community is extremely clever, so it’s only just begun.
Parallel Attacks and GPUs
Since your CPU can only guess a few hashes per second, PBKDF2 is a thorny problem to contend with.
However, there’s an easy way for attackers to use commodity hardware to bypass this limitation: Graphics cards are specially designed to perform a lot of low-memory calculations in parallel.
If you can write your password cracking code to leverage the benefits of GPUs instead of CPUs, then PBKDF2 becomes easy potatoes.
The other secure password hashing algorithm in use at the time, bcrypt, had only a linear improvement over PBKDF2’s security against GPU attacks.
Memory-Hard Password Hashing Algorithms
In 2009, Colin Percival proposed scrypt to mitigate this risk. Scrypt (pronounced “ess crypt”) builds atop PBKDF2-SHA256 by hashing psuedorandom regions of memory with Salsa20/8 (hence the S in Scrypt) in a way that makes it difficult to precompute.
Scrypt hashes require large amounts of memory to compute (at least 16 megabytes, in the recommended minimum configuration, versus the few kilobytes of incumbent password hashes).
While GPUs (and FPGAs, and ASICs, and …) are great for cracking password hashes that use CPU-bounded algorithms, algorithms that access large amounts of memory are difficult to attack effectively.
It’s still possible for clever programmers to work around this memory/bandwidth limitation, but to do so, you must compute more operations, which makes it not worthwhile.
Cryptographers and the password-cracking community call this expensive time-memory trade-off memory hardness. In 2016, it was determined that scrypt is maximally memory-hard.
Password Hashing Competition
The Password Hashing Competition (PHC) was kicked off by JP Aumasson in 2012 to develop a new standard for password hashing and password-based key derivation.
In 2015, they selected Argon2 as its recommendation, with four finalists receiving special recognition (Catena, Lyra2, Makwa, and yescrypt–which is based on scrypt).
Cache-Hardness
In the years since the PHC concluded, the advances in password cracking techniques have not slowed down.
One of the PHC judges recently proposed a new algorithm called bscrypt which purports a property called “cache hard” rather than “memory hard”. The reasoning is that, for shorter run times, memory bandwidth and small CPU caches is a tighter bottleneck than overall memory requirements.
In fact, there’s an Argon2 variant (Argon2ds) which offers cache-hardness.
Two Hard Choices
So which of the two should you care about, as a defender?
If you’re validating password hashes in an online service, a cache-hard algorithm might make more sense. You’re incentivized to have shorter server-side run times to avoid DoS attacks, so the benefits of cache-hardness seem more impactful than memory-hardness.
If you’re deriving a sensitive cryptography key from a password and can afford to take several seconds of wall-clock time, a memory-hard algorithm is likely to be a better fit for your threat model.
(Or, like, run both a cache-hard and memory-hard algorithm and use a fast KDF, such as HKDF, to mix the two into your final cryptography key.)
Of course, the story doesn’t end here. Password Hashing and Password-Based Key Derivation continues to mature as the password cracking community discovers new attacks and engineers defenses against them.

A Strange Game; The Only Winning Move is to PAKE
Password hashing is a defense-in-depth against a system compromise that enables attackers to perform offline attacks against a cryptographic output to determine a user’s password.
However, for many applications, the bigger question is, “Why even play this game in the first place?”
Password-Authenticated Key Exchanges
A password authenticated key exchange (PAKE) algorithm is an interactive protocol to establish keys based on at least one party’s knowledge of a password.
PAKEs are what enable you to log into encrypted WiFi connections and encrypt your traffic. PAKEs prevent you from having to reveal the password (or a password-equivalent value, such as a password hash) to the other party.
Although there are a lot of proposed PAKE algorithms, the one that most people implemented was SRP (“Secure Remote Password”), which was intuitively a lot like Diffie-Hellman but also not Diffie-Hellman (since SRP used addition).
For a good teardown on SRP, Matthew Green’s blog is highly recommended.
There are a few real-world cryptography problems with using SRP:
- You need to use a special kind of prime number for your protocol. The standard Diffie-Hellman moduli are not suitable for SRP; you want a safe prime (i.e. a number of the form N = 2q + 1, where q is also prime).
- One of the steps in SRP, client-side, is to compute
A = g^a (mod N). Here,Ais a public value whileais a secret (usually the SHA1 hash of the username and pasword).
If your software implementation of modular exponentiation (a^x mod P) isn’t constant-time, you leaka, which is a password-equivalent value.
Additionally, it’s not possible to use SRP with elliptic curve groups. (Matthew Green’s post I linked above covers this in detail!)
Thus, SRP is generally considered to be deprecated by security experts, in favor of other PAKEs.
IETF, CFRG, PAKE Selection
As early as IETF 104, the Crypto Forum Research Group (CFRG) began exploring different PAKE algorithms to select for standardization.
One of the motivators for this work is that the WiFi alliance had shoehorned a new PAKE called Dragonfly into their WPA3, which turned out to be badly designed.
The CFRG’s candidate algorithms and reviews were publicly tracked on GitHub, if you’re curious.
TL;DR – They settled on recommending OPAQUE as an augmented PAKE and CPace as a balanced PAKE.
Sc00bz has done multiple talks at security conferences over the years to talk about PAKEs:
https://www.youtube.com/watch?v=28SM5ILpHEE
Quantum Annoyance
The PAKEs we’ve discussed involved a cyclic group (and the newer ones involved an elliptic curve group). The security of these schemes is dependent on the hardness of a discrete logarithm problem.
If a cryptography relevant quantum computer (CRQC) is developed, discrete logarithm problems will cease to be hard.
Some PAKEs fall apart the moment a discrete log is solvable. This is par for the course for Diffie-Hellman and elliptic curve cryptography.
Others require an attacker to solve a discrete log for every guess in an offline attack (after capturing a successful exchange). This makes them annoying for quantum attackers.
While they don’t provide absolute security like post-quantum cryptography, they do make attackers armed with a CRQC work harder.
OPAQUE isn’t quantum annoying. Simply observe all of the packets from making an online guess, solve the DLP offline, and you’re back to the realm of classical offline guessing.

The State of the Art
At this point, you may feel somewhat overwhelmed by all of this information. It’s very tempting to simplify all of this historical context and technical detail.
You might be telling yourself, “Okay, Scrypt, Argon2, CPace, OPAQUE. Got it. That’s all I need to remember. Everything else is questionable at best. Ask a cryptographer. I’m bailing out, yo!”
But the story gets worse on two fronts: Real-world operational requirements, and compliance.
Your Hands Are Tied, Now Swim
If you’re selling a product or service to the US government that uses cryptography, you need to first clear a bare minimum bar called FIPS 140.
FIPS 140 is opinionated about which algorithms you use. For password hashing and password-based key derivation, FIPS defers to NIST SP 800-209, which means you’re only permitted to use PBKDF2 in any FIPS modules (with a SHA2- family hash function). (Update: See below.)
So all of the information about memory-hard and cache-hard password hashing algorithms? This is useless for you if you ever try to sell to the US government.
An open question is whether Scrypt is FIPSable due to it building atop PBKDF2. To be blunt: I’m not sure. Ask a NIST Cryptographic Module Validation Program lab for their opinion.
Update (2022-01-07): A Brief Correction
Thanks to FreakLegion for pointing this out.
According to NIST SP 800-63B, memory-hard hash functions are recommended.
Examples of suitable key derivation functions include Password-based Key Derivation Function 2 (PBKDF2) [SP 800-132] and Balloon [BALLOON]. A memory-hard function SHOULD be used because it increases the cost of an attack.NIST SP 800-63B
Don’t use Balloon, though. It’s under-specified.
FreakLegion indicates in their Hacker News comment that scrypt and yescrypt are both acceptable.
End Update
In the realm of PAKEs, both CPace and OPAQUE are frameworks that can be used with multiple elliptic curve groups.
Both frameworks support NIST P-256, but CPace supports X25519 and OPAQUE supports Ristretto255; these are currently not FIPSable curves.
“I don’t care about FIPS. Argon2 all the things!”
JavaScript runtimes don’t provide a built-in Argon2 implementation. This poses several challenges.
- Do you care about iOS users? Lockdown mode prevents you from using WebAssembly, even in a browser extension.
- Trying to polyfill scrypt or Argon2 in a scripting language is a miserable experience. We’re talking quadratic performance penalties here. Several minutes of CPU time to calculate a hash that is far too weak to be acceptable in any context.
Consequently, not a single password manager I’ve evaluated that provides a browser extension uses a memory-hard algorithm for deriving encryption keys.
Update: I’ve been told Dashlane uses Argon2.

This Is Frustrating
When I write about cryptography, my goal is always to be clear, concise, and helpful. I want whoever reads my writing to, regardless of their level of expertise, walk away more comfortable with the subject matter.
At minimum, I want you to be able to intuit when you need to ask an expert for help, and have a slightly better understanding of how to word your questions to get the answer you need. In an ideal world, you’d even be able to spot the same kind of weaknesses I do in cryptography designs and implementations after reading enough of this blog.
I can’t do that with password-based cryptography. The use-cases and threat models are too varied to make a clear-cut recommendation, and it’s too complicated to parcel out in a way that doesn’t feel reductive or slightly contradictory. This leads to too many caveats or corner cases.
Passwords suck.
If you ask a password cracking expert and describe your use case, you’ll likely get an opinionated and definitive answer. But every time I’ve asked generally about this subject, without a specific use case in mind, I got an opinionated answer followed by a long chain of caveats and alternatives.
With that in mind, here’s a few vague guidelines that are up-to-date as of the end of 2022.

Recommendations for Password-Based Cryptography in 2023
Password Hashing
If you’re authenticating users in an online service (storing the hashes in a database), use any of the following algorithms:
- bcrypt with a cost factor appropriate to take about 100 milliseconds to compute on your server hardware (typically at least 12)
- scrypt with N = 32768, r = 8, p = 1 and a random salt at least 128 bits in length (256 preferred)
- Argon2id with a memory cost of 64 MiB, ops cost of 3, and parallelism of 1
If you’re forced to use PBKDF2 for whatever dumb reason, the parameters you want are at least:
- SHA-512 with 210,000 rounds (preferred)
- SHA-256 with 600,000 rounds
- SHA-1 (if you must) with 1,300,000 rounds
These numbers are based on constraining attackers to less than 10,000 hashes per second, per GPU.
I’m not currently recommending any algorithms deliberately designed for cache-hardness because they need further analysis from other cryptographers. (Bcrypt is minimally cache-hard, but that wasn’t a stated design goal.)
I didn’t evaluate the other PHC finalists nor other designs (Balloon hashing, Ball and Chain, etc.). Ask your cryptographer if those are appropriate instead.
Password-Based Key Derivation
If you’re deriving an encryption key from a password, use any of the following algorithms:
- scrypt with N = 1048576, r = 8, p = 1 and a random salt at least 128 bits in length (256 preferred)
- Argon2id with a memory cost of 1024 MiB, ops cost of 4, and parallelism of 1
If you’re forced to use PBKDF2 for whatever dumb reason, the parameters you want should target between 1 and 10 seconds on the defender’s hardware. If this is somehow slower than the numbers given for password hashing above, go with the password hashing benchmarks instead.
Here’s a dumb PHP script you can use to quickly find some target numbers.
<?php/* Dumb PBKDF2 benchmarking script by Soatok. 2022-12-29 */$salt = random_bytes(32);$password = 'correct horse battery staple';$c = '';$start = $end = microtime(true);foreach(['sha1', 'sha256', 'sha512'] as $alg) {foreach ([1 << 14,1 << 15,1 << 16,1 << 17,1 << 18,1 << 19,1 << 20,1200000,1 << 21,2500000,3000000,3500000,1 << 22,5000000,1 << 23,1 << 24,1 << 25,] as $n) { $start = microtime(true); $c ^= hash_pbkdf2($alg, $password, $salt, $n, 32, true); $end = microtime(true); $time = $end - $start; echo str_pad($n, 12, ' ', STR_PAD_LEFT), " iterations ({$alg}) -> \t", $time, PHP_EOL; if ($time > 5.5) { echo PHP_EOL; break; }}}
On my laptop, targeting 5.0 seconds means at least 4,000,000 rounds of PBKDF2 with SHA1, SHA256, or SHA512 (with SHA256 coming closer to 5,000,000).
If you’re aiming for less than 1,000 hashes per second per GPU, against an attacker armed with an RTX 4090:
- SHA-512 with 3,120,900 iterations (preferred)
- SHA256 with 8,900,000 iterations
- SHA-1 with 20,000,000 iterations
Sc00bz tells me that this generation of GPU has better performance/cost than previous generations (which had seen diminishing returns), but requires 1.5x the power, 1.78x the price, and 2x the physical space. Sc00bz refers to this as “1.5 GPUs”.
If you adjust for these factors, your final PBKDF2 target becomes:
- SHA-512 with 2,100,000 iterations (preferred)
- SHA-256 with 6,000,000 iterations
- SHA-1 with 13,000,000 iterations
Password Authenticated Key Exchanges
In a client-server model, where the server isn’t meant to see password-equivalent data, you want an augmented PAKE (or perhaps a doubly-augmented PAKE).
You’re overwhelmingly more likely to find OPAQUE support in the immediate future, due to the direction the IETF CFRG is moving today.
In a more peer-to-peer model, you want a balanced PAKE. CPace is the best game in town.
Don’t use SRP if you can help it.
If you can’t help it, make sure you use one of the groups defined in RFC 5054, rather than a generic Diffie-Hellman group. You’ll also want an expert to review your implementation to make sure your BigInt library isn’t leaking your users’ private exponents.
Also, feel free to deviate from SHA1 for calculating the private exponent from their username and password. SHA1 sucks. Nothing is stopping you from using a password KDF (or, at worst, SHA256) here, as long as you do so consistently.
(But as always, ask your cryptography expert first.)

TL;DR
Password-Based Cryptography is a mess.
If you’re not aware of the history of the field and the technical details that went into the various cryptographic algorithms that experts recommend today, it’s very easy to say something wrong that sounds correct to an untrained ear.
At the end of the day, the biggest risk you face with password-based cryptography is not using a suitable algorithm in the first place, rather than using a less optimal algorithm.
Experts have good reasons to hate PBDKF2 (slow for defenders, fast for attackers) and SRP (we have better options today, which also come with actual security proofs), but they certainly hate unsalted SHA1 and Triple-DES more.
My only real contribution to this topic is an effort to make it easier to talk about to non-experts by offering a new term for the superset of all of these password-based algorithms: Password-Based Cryptographic Functions.
Finally, the password cracking community is great. There are a lot of smart and friendly people involved, and they’re all working to make this problem easier to get right. If you’re not sure where to start, check out PasswordsCon.

https://soatok.blog/2022/12/29/what-we-do-in-the-etc-shadow-cryptography-with-passwords/
#cryptographicHashFunction #cryptographicProtocols #OPAQUE #passwordHashing #PBKDF2 #SecureRemotePasswordProtocol #SecurityGuidance
NIST opened public comments on SP 800-108 Rev. 1 (the NIST recommendations for Key Derivation Functions) last month. The main thing that’s changed from the original document published in 2009 is the inclusion of the Keccak-based KMAC alongside the incumbent algorithms.One of the recommendations of SP 800-108 is called “KDF in Counter Mode”. A related document, SP 800-56C, suggests using a specific algorithm called HKDF instead of the generic Counter Mode construction from SP 800-108–even though they both accomplish the same goal.
Isn’t standards compliance fun?
Interestingly, HKDF isn’t just an inconsistently NIST-recommended KDF, it’s also a common building block in a software developer’s toolkit which sees a lot of use in different protocols.
Unfortunately, the way HKDF is widely used is actually incorrect given its formal security definition. I’ll explain what I mean in a moment.
Art: Scruff
What is HKDF?
To first understand what HKDF is, you first need to know about HMAC.HMAC is a standard message authentication code (MAC) algorithm built with cryptographic hash functions (that’s the H). HMAC is specified in RFC 2104 (yes, it’s that old).
HKDF is a key-derivation function that uses HMAC under-the-hood. HKDF is commonly used in encryption tools (Signal, age). HKDF is specified in RFC 5869.
HKDF is used to derive a uniformly-random secret key, typically for use with symmetric cryptography algorithms. In any situation where a key might need to be derived, you might see HKDF being used. (Although, there may be better algorithms.)
Art: LvJ
How Developers Understand and Use HKDF
If you’re a software developer working with cryptography, you’ve probably seen an API in the crypto module for your programming language that looks like this, or maybe this.hash_hkdf( string $algo, string $key, int $length = 0, string $info = "", string $salt = ""): string
Software developers that work with cryptography will typically think of the HKDF parameters like so:
$algo— which hash function to use$key— the input key, from which multiple keys can be derived$length— how many bytes to derive$info— some arbitrary string used to bind a derived key to an intended context$salt— some additional randomness (optional)The most common use-case of HKDF is to implement key-splitting, where a single input key (the Initial Keying Material, or IKM) is used to derive two or more independent keys, so that you’re never using a single key for multiple algorithms.
See also:
[url=https://github.com/defuse/php-encryption]defuse/php-encryption[/url], a popular PHP encryption library that does exactly what I just described.At a super high level, the HKDF usage I’m describing looks like this:
class MyEncryptor {protected function splitKeys(CryptographyKey $key, string $salt): array { $encryptKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, 'encryption', $salt )); $authKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, 'message authentication', $salt )); return [$encryptKey, $authKey];}public function encryptString(string $plaintext, CryptographyKey $key): string{ $salt = random_bytes(32); [$encryptKey, $hmacKey] = $this->splitKeys($key, $salt); // ... encryption logic here ... return base64_encode($salt . $ciphertext . $mac);}public function decryptString(string $encrypted, CryptographyKey $key): string{ $decoded = base64_decode($encrypted); $salt = mb_substr($decoded, 0, 32, '8bit'); [$encryptKey, $hmacKey] = $this->splitKeys($key, $salt); // ... decryption logic here ... return $plaintext;}// ... other method here ...}
Unfortunately, anyone who ever does something like this just violated one of the core assumptions of the HKDF security definition and no longer gets to claim “KDF security” for their construction. Instead, your protocol merely gets to claim “PRF security”.
Art: Harubaki
KDF? PRF? OMGWTFBBQ?
Let’s take a step back and look at some basic concepts.(If you want a more formal treatment, read this Stack Exchange answer.)
PRF: Pseudo-Random Functions
A pseudorandom function (PRF) is an efficient function that emulates a random oracle.“What the hell’s a random oracle?” you ask? Well, Thomas Pornin has the best explanation for random oracles:
A random oracle is described by the following model:
- There is a black box. In the box lives a gnome, with a big book and some dice.
- We can input some data into the box (an arbitrary sequence of bits).
- Given some input that he did not see beforehand, the gnome uses his dice to generate a new output, uniformly and randomly, in some conventional space (the space of oracle outputs). The gnome also writes down the input and the newly generated output in his book.
- If given an already seen input, the gnome uses his book to recover the output he returned the last time, and returns it again.
So a random oracle is like a kind of hash function, such that we know nothing about the output we could get for a given input message m. This is a useful tool for security proofs because they allow to express the attack effort in terms of number of invocations to the oracle.
The problem with random oracles is that it turns out to be very difficult to build a really “random” oracle. First, there is no proof that a random oracle can really exist without using a gnome. Then, we can look at what we have as candidates: hash functions. A secure hash function is meant to be resilient to collisions, preimages and second preimages. These properties do not imply that the function is a random oracle.
Thomas Pornin
Alternatively, Wikipedia has a more formal definition available to the academic-inclined.In practical terms, we can generate a strong PRF out of secure cryptographic hash functions by using a keyed construction; i.e. HMAC.
Thus, as long as your HMAC key is a secret, the output of HMAC can be generally treated as a PRF for all practical purposes. Your main security consideration (besides key management) is the collision risk if you truncate its output.
Art: LvJ
KDF: Key Derivation Functions
A key derivation function (KDF) is exactly what it says on the label: a cryptographic algorithm that derives one or more cryptographic keys from a secret input (which may be another cryptography key, a group element from a Diffie-Hellman key exchange, or a human-memorable password).Note that passwords should be used with a Password-Based Key Derivation Function, such as scrypt or Argon2id, not HKDF.
Despite what you may read online, KDFs do not need to be built upon cryptographic hash functions, specifically; but in practice, they often are.
A notable counter-example to this hash function assumption: CMAC in Counter Mode (from NIST SP 800-108) uses AES-CMAC, which is a variable-length input variant of CBC-MAC. CBC-MAC uses a block cipher, not a hash function.
Regardless of the construction, KDFs use a PRF under the hood, and the output of a KDF is supposed to be a uniformly random bit string.
Art: LvJ
PRF vs KDF Security Definitions
The security definition for a KDF has more relaxed requirements than PRFs: PRFs require the secret key be uniformly random. KDFs do not have this requirement.If you use a KDF with a non-uniformly random IKM, you probably need the KDF security definition.
If your IKM is already uniformly random (i.e. the “key separation” use case), you can get by with just a PRF security definition.
After all, the entire point of KDFs is to allow a congruent security level as you’d get from uniformly random secret keys, without also requiring them.
However, if you’re building a protocol with a security requirement satisfied by a KDF, but you actually implemented a PRF (i.e., not a KDF), this is a security vulnerability in your cryptographic design.
Art: LvJ
The HKDF Algorithm
HKDF is an HMAC-based KDF. Its algorithm consists of two distinct steps:
HKDF-Extractuses the Initial Keying Material (IKM) and Salt to produce a Pseudo-Random Key (PRK).HKDF-Expandactually derives the keys using PRK, theinfoparameter, and a counter (from0to255) for each hash function output needed to generate the desired output length.If you’d like to see an implementation of this algorithm,
defuse/php-encryptionprovides one (since it didn’t land in PHP until 7.1.0). Alternatively, there’s a Python implementation on Wikipedia that uses HMAC-SHA256.This detail about the two steps will matter a lot in just a moment.
Art: Swizz
How HKDF Salts Are Misused
The HKDF paper, written by Hugo Krawczyk, contains the following definition (page 7).
The paper goes on to discuss the requirements for authenticating the salt over the communication channel, lest the attacker have the ability to influence it.
A subtle detail of this definition is that the security definition says that A salt value
, not Multiple salt values.
Which means: You’re not supposed to use HKDF with a constant IKM, info label, etc. but vary the salt for multiple invocations. The salt must either be a fixed random value, or NULL.
The HKDF RFC makes this distinction even less clear when it argues for random salts.
We stress, however, that the use of salt adds significantly to the strength of HKDF, ensuring independence between different uses of the hash function, supporting “source-independent” extraction, and strengthening the analytical results that back the HKDF design.Random salt differs fundamentally from the initial keying material in two ways: it is non-secret and can be re-used. As such, salt values are available to many applications. For example, a pseudorandom number generator (PRNG) that continuously produces outputs by applying HKDF to renewable pools of entropy (e.g., sampled system events) can fix a salt value and use it for multiple applications of HKDF without having to protect the secrecy of the salt. In a different application domain, a key agreement protocol deriving cryptographic keys from a Diffie-Hellman exchange can derive a salt value from public nonces exchanged and authenticated between communicating parties as part of the key agreement (this is the approach taken in [IKEv2]).
RFC 5869, section 3.1
Okay, sure. Random salts are better than a NULL salt. And while this section alludes to “[fixing] a salt value” to “use it for multiple applications of HKDF without having to protect the secrecy of the salt”, it never explicitly states this requirement. Thus, the poor implementor is left to figure this out on their own.Thus, because it’s not using HKDF in accordance with its security definition, many implementations (such as the PHP encryption library we’ve been studying) do not get to claim that their construction has KDF security.
Instead, they only get to claim “Strong PRF” security, which you can get from just using HMAC.
Art: LvJ
What Purpose Do HKDF Salts Actually Serve?
Recall that the HKDF algorithm uses salts in the HDKF-Extract step. Salts in this context were intended for deriving keys from a Diffie-Hellman output, or a human-memorable password.In the case of [Elliptic Curve] Diffie-Hellman outputs, the result of the key exchange algorithm is a random group element, but not necessarily uniformly random bit string. There’s some structure to the output of these functions. This is why you always, at minimum, apply a cryptographic hash function to the output of [EC]DH before using it as a symmetric key.
HKDF uses salts as a mechanism to improve the quality of randomness when working with group elements and passwords.
Extending the nonce for a symmetric-key AEAD mode is a good idea, but using HKDF’s salt parameter specifically to accomplish this is a misuse of its intended function, and produces a weaker argument for your protocol’s security than would otherwise be possible.
How Should You Introduce Randomness into HKDF?
Just shove it in theinfoparameter.
Art: LvJ
It may seem weird, and defy intuition, but the correct way to introduce randomness into HKDF as most developers interact with the algorithm is to skip the salt parameter entirely (either fixing it to a specific value for domain-separation or leaving it NULL), and instead concatenate data into the
infoparameter.class BetterEncryptor extends MyEncryptor {protected function splitKeys(CryptographyKey $key, string $salt): array { $encryptKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, $salt . 'encryption', '' // intentionally empty )); $authKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, $salt . 'message authentication', '' // intentionally empty )); return [$encryptKey, $authKey];}}
Of course, you still have to watch out for canonicalization attacks if you’re feeding multi-part messages into the info tag.
Another advantage: This also lets you optimize your HKDF calls by caching the PRK from the
HKDF-Extractstep and reuse it for multiple invocations ofHKDF-Expandwith a distinctinfo. This allows you to reduce the number of hash function invocations fromto
(since each HMAC involves two hash function invocations).
Notably, this HKDF salt usage was one of the things that was changed in V3/V4 of PASETO.
Does This Distinction Really Matter?
If it matters, your cryptographer will tell you it matters–which probably means they have a security proof that assumes the KDF security definition for a very good reason, and you’re not allowed to violate that assumption.Otherwise, probably not. Strong PRF security is still pretty damn good for most threat models.
Art: LvJ
Closing Thoughts
If your takeaway was, “Wow, I feel stupid,” don’t, because you’re in good company.I’ve encountered several designs in my professional life that shoved the randomness into the
infoparameter, and it perplexed me because there was a perfectly good salt parameter right there. It turned out, I was wrong to believe that, for all of the subtle and previously poorly documented reasons discussed above. But now we both know, and we’re all better off for it.So don’t feel dumb for not knowing. I didn’t either, until this was pointed out to me by a very patient colleague.
“Feeling like you were stupid” just means you learned.
(Art: LvJ)Also, someone should really get NIST to be consistent about whether you should use HKDF or “KDF in Counter Mode with HMAC” as a PRF, because SP 800-108’s new revision doesn’t concede this point at all (presumably a relic from the 2009 draft).
This concession was made separately in 2011 with SP 800-56C revision 1 (presumably in response to criticism from the 2010 HKDF paper), and the present inconsistency is somewhat vexing.
(On that note, does anyone actually use the NIST 800-108 KDFs instead of HKDF? If so, why? Please don’t say you need CMAC…)
Bonus Content
These questions were asked after this blog post initially went public, and I thought they were worth adding. If you ask a good question, it may end up being edited in at the end, too.
Art: LvJ
Why Does HKDF use the Salt as the HMAC key in the Extract Step? (via r/crypto)
Broadly speaking, when applying a PRF to two “keys”, you get to decide which one you treat as the “key” in the underlying API.HMAC’s API is HMACalg(key, message), but how HKDF uses it might as well be HMACalg(key1, key2).
The difference here seems almost arbitrary, but there’s a catch.
HKDF was designed for Diffie-Hellman outputs (before ECDH was the norm), which are generally able to be much larger than the block size of the underlying hash function. 2048-bit DH results fit in 256 bytes, which is 4 times the SHA256 block size.
If you have to make a decision, using the longer input (DH output) as the message is more intuitive for analysis than using it as the key, due to pre-hashing. I’ve discussed the counter-intuitive nature of HMAC’s pre-hashing behavior at length in this post, if you’re interested.
So with ECDH, it literally doesn’t matter which one was used (unless you have a weird mismatch in hash functions and ECC groups; i.e. NIST P-521 with SHA-224).
But before the era of ECDH, it was important to use the salt as the HMAC key in the extract step, since they were necessarily smaller than a DH group element.
Thus, HKDF chose HMACalg(salt, IKM) instead of HMACalg(IKM, salt) for the calculation of PRK in the HKDF-Extract step.
Neil Madden also adds that the reverse would create a chicken-egg situation, but I personally suspect that the pre-hashing would be more harmful to the security analysis than merely supplying a non-uniformly random bit string as an HMAC key in this specific context.
My reason for believing this is, when a salt isn’t supplied, it defaults to a string of
0x00bytes as long as the output size of the underlying hash function. If the uniform randomness of the salt mattered that much, this wouldn’t be a tolerable condition.https://soatok.blog/2021/11/17/understanding-hkdf/
#cryptographicHashFunction #cryptography #hashFunction #HMAC #KDF #keyDerivationFunction #securityDefinition #SecurityGuidance

NIST opened public comments on SP 800-108 Rev. 1 (the NIST recommendations for Key Derivation Functions) last month. The main thing that’s changed from the original document published in 2009 is the inclusion of the Keccak-based KMAC alongside the incumbent algorithms.
One of the recommendations of SP 800-108 is called “KDF in Counter Mode”. A related document, SP 800-56C, suggests using a specific algorithm called HKDF instead of the generic Counter Mode construction from SP 800-108–even though they both accomplish the same goal.
Isn’t standards compliance fun?
Interestingly, HKDF isn’t just an inconsistently NIST-recommended KDF, it’s also a common building block in a software developer’s toolkit which sees a lot of use in different protocols.
Unfortunately, the way HKDF is widely used is actually incorrect given its formal security definition. I’ll explain what I mean in a moment.

What is HKDF?
To first understand what HKDF is, you first need to know about HMAC.
HMAC is a standard message authentication code (MAC) algorithm built with cryptographic hash functions (that’s the H). HMAC is specified in RFC 2104 (yes, it’s that old).
HKDF is a key-derivation function that uses HMAC under-the-hood. HKDF is commonly used in encryption tools (Signal, age). HKDF is specified in RFC 5869.
HKDF is used to derive a uniformly-random secret key, typically for use with symmetric cryptography algorithms. In any situation where a key might need to be derived, you might see HKDF being used. (Although, there may be better algorithms.)

How Developers Understand and Use HKDF
If you’re a software developer working with cryptography, you’ve probably seen an API in the crypto module for your programming language that looks like this, or maybe this.
hash_hkdf( string $algo, string $key, int $length = 0, string $info = "", string $salt = ""): string
Software developers that work with cryptography will typically think of the HKDF parameters like so:
$algo— which hash function to use$key— the input key, from which multiple keys can be derived$length— how many bytes to derive$info— some arbitrary string used to bind a derived key to an intended context$salt— some additional randomness (optional)
The most common use-case of HKDF is to implement key-splitting, where a single input key (the Initial Keying Material, or IKM) is used to derive two or more independent keys, so that you’re never using a single key for multiple algorithms.
See also: [url=https://github.com/defuse/php-encryption]defuse/php-encryption[/url], a popular PHP encryption library that does exactly what I just described.
At a super high level, the HKDF usage I’m describing looks like this:
class MyEncryptor {protected function splitKeys(CryptographyKey $key, string $salt): array { $encryptKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, 'encryption', $salt )); $authKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, 'message authentication', $salt )); return [$encryptKey, $authKey];}public function encryptString(string $plaintext, CryptographyKey $key): string{ $salt = random_bytes(32); [$encryptKey, $hmacKey] = $this->splitKeys($key, $salt); // ... encryption logic here ... return base64_encode($salt . $ciphertext . $mac);}public function decryptString(string $encrypted, CryptographyKey $key): string{ $decoded = base64_decode($encrypted); $salt = mb_substr($decoded, 0, 32, '8bit'); [$encryptKey, $hmacKey] = $this->splitKeys($key, $salt); // ... decryption logic here ... return $plaintext;}// ... other method here ...}
Unfortunately, anyone who ever does something like this just violated one of the core assumptions of the HKDF security definition and no longer gets to claim “KDF security” for their construction. Instead, your protocol merely gets to claim “PRF security”.

KDF? PRF? OMGWTFBBQ?
Let’s take a step back and look at some basic concepts.
(If you want a more formal treatment, read this Stack Exchange answer.)
PRF: Pseudo-Random Functions
A pseudorandom function (PRF) is an efficient function that emulates a random oracle.
“What the hell’s a random oracle?” you ask? Well, Thomas Pornin has the best explanation for random oracles:
A random oracle is described by the following model:
- There is a black box. In the box lives a gnome, with a big book and some dice.
- We can input some data into the box (an arbitrary sequence of bits).
- Given some input that he did not see beforehand, the gnome uses his dice to generate a new output, uniformly and randomly, in some conventional space (the space of oracle outputs). The gnome also writes down the input and the newly generated output in his book.
- If given an already seen input, the gnome uses his book to recover the output he returned the last time, and returns it again.
So a random oracle is like a kind of hash function, such that we know nothing about the output we could get for a given input message m. This is a useful tool for security proofs because they allow to express the attack effort in terms of number of invocations to the oracle.
The problem with random oracles is that it turns out to be very difficult to build a really “random” oracle. First, there is no proof that a random oracle can really exist without using a gnome. Then, we can look at what we have as candidates: hash functions. A secure hash function is meant to be resilient to collisions, preimages and second preimages. These properties do not imply that the function is a random oracle.
Thomas Pornin
Alternatively, Wikipedia has a more formal definition available to the academic-inclined.
In practical terms, we can generate a strong PRF out of secure cryptographic hash functions by using a keyed construction; i.e. HMAC.
Thus, as long as your HMAC key is a secret, the output of HMAC can be generally treated as a PRF for all practical purposes. Your main security consideration (besides key management) is the collision risk if you truncate its output.

KDF: Key Derivation Functions
A key derivation function (KDF) is exactly what it says on the label: a cryptographic algorithm that derives one or more cryptographic keys from a secret input (which may be another cryptography key, a group element from a Diffie-Hellman key exchange, or a human-memorable password).
Note that passwords should be used with a Password-Based Key Derivation Function, such as scrypt or Argon2id, not HKDF.
Despite what you may read online, KDFs do not need to be built upon cryptographic hash functions, specifically; but in practice, they often are.
A notable counter-example to this hash function assumption: CMAC in Counter Mode (from NIST SP 800-108) uses AES-CMAC, which is a variable-length input variant of CBC-MAC. CBC-MAC uses a block cipher, not a hash function.
Regardless of the construction, KDFs use a PRF under the hood, and the output of a KDF is supposed to be a uniformly random bit string.

PRF vs KDF Security Definitions
The security definition for a KDF has more relaxed requirements than PRFs: PRFs require the secret key be uniformly random. KDFs do not have this requirement.
If you use a KDF with a non-uniformly random IKM, you probably need the KDF security definition.
If your IKM is already uniformly random (i.e. the “key separation” use case), you can get by with just a PRF security definition.
After all, the entire point of KDFs is to allow a congruent security level as you’d get from uniformly random secret keys, without also requiring them.
However, if you’re building a protocol with a security requirement satisfied by a KDF, but you actually implemented a PRF (i.e., not a KDF), this is a security vulnerability in your cryptographic design.

The HKDF Algorithm
HKDF is an HMAC-based KDF. Its algorithm consists of two distinct steps:
HKDF-Extractuses the Initial Keying Material (IKM) and Salt to produce a Pseudo-Random Key (PRK).HKDF-Expandactually derives the keys using PRK, theinfoparameter, and a counter (from0to255) for each hash function output needed to generate the desired output length.
If you’d like to see an implementation of this algorithm, defuse/php-encryption provides one (since it didn’t land in PHP until 7.1.0). Alternatively, there’s a Python implementation on Wikipedia that uses HMAC-SHA256.
This detail about the two steps will matter a lot in just a moment.

How HKDF Salts Are Misused
The HKDF paper, written by Hugo Krawczyk, contains the following definition (page 7).
The paper goes on to discuss the requirements for authenticating the salt over the communication channel, lest the attacker have the ability to influence it.
A subtle detail of this definition is that the security definition says that A salt value 
Which means: You’re not supposed to use HKDF with a constant IKM, info label, etc. but vary the salt for multiple invocations. The salt must either be a fixed random value, or NULL.
The HKDF RFC makes this distinction even less clear when it argues for random salts.
We stress, however, that the use of salt adds significantly to the strength of HKDF, ensuring independence between different uses of the hash function, supporting “source-independent” extraction, and strengthening the analytical results that back the HKDF design.Random salt differs fundamentally from the initial keying material in two ways: it is non-secret and can be re-used. As such, salt values are available to many applications. For example, a pseudorandom number generator (PRNG) that continuously produces outputs by applying HKDF to renewable pools of entropy (e.g., sampled system events) can fix a salt value and use it for multiple applications of HKDF without having to protect the secrecy of the salt. In a different application domain, a key agreement protocol deriving cryptographic keys from a Diffie-Hellman exchange can derive a salt value from public nonces exchanged and authenticated between communicating parties as part of the key agreement (this is the approach taken in [IKEv2]).
RFC 5869, section 3.1
Okay, sure. Random salts are better than a NULL salt. And while this section alludes to “[fixing] a salt value” to “use it for multiple applications of HKDF without having to protect the secrecy of the salt”, it never explicitly states this requirement. Thus, the poor implementor is left to figure this out on their own.
Thus, because it’s not using HKDF in accordance with its security definition, many implementations (such as the PHP encryption library we’ve been studying) do not get to claim that their construction has KDF security.
Instead, they only get to claim “Strong PRF” security, which you can get from just using HMAC.

What Purpose Do HKDF Salts Actually Serve?
Recall that the HKDF algorithm uses salts in the HDKF-Extract step. Salts in this context were intended for deriving keys from a Diffie-Hellman output, or a human-memorable password.
In the case of [Elliptic Curve] Diffie-Hellman outputs, the result of the key exchange algorithm is a random group element, but not necessarily uniformly random bit string. There’s some structure to the output of these functions. This is why you always, at minimum, apply a cryptographic hash function to the output of [EC]DH before using it as a symmetric key.
HKDF uses salts as a mechanism to improve the quality of randomness when working with group elements and passwords.
Extending the nonce for a symmetric-key AEAD mode is a good idea, but using HKDF’s salt parameter specifically to accomplish this is a misuse of its intended function, and produces a weaker argument for your protocol’s security than would otherwise be possible.
How Should You Introduce Randomness into HKDF?
Just shove it in the info parameter.

It may seem weird, and defy intuition, but the correct way to introduce randomness into HKDF as most developers interact with the algorithm is to skip the salt parameter entirely (either fixing it to a specific value for domain-separation or leaving it NULL), and instead concatenate data into the info parameter.
class BetterEncryptor extends MyEncryptor {protected function splitKeys(CryptographyKey $key, string $salt): array { $encryptKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, $salt . 'encryption', '' // intentionally empty )); $authKey = new CryptographyKey(hash_hkdf( 'sha256', $key->getRawBytes(), 32, $salt . 'message authentication', '' // intentionally empty )); return [$encryptKey, $authKey];}}
Of course, you still have to watch out for canonicalization attacks if you’re feeding multi-part messages into the info tag.
Another advantage: This also lets you optimize your HKDF calls by caching the PRK from the HKDF-Extract step and reuse it for multiple invocations of HKDF-Expand with a distinct info. This allows you to reduce the number of hash function invocations from 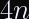
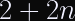
Notably, this HKDF salt usage was one of the things that was changed in V3/V4 of PASETO.
Does This Distinction Really Matter?
If it matters, your cryptographer will tell you it matters–which probably means they have a security proof that assumes the KDF security definition for a very good reason, and you’re not allowed to violate that assumption.
Otherwise, probably not. Strong PRF security is still pretty damn good for most threat models.

Closing Thoughts
If your takeaway was, “Wow, I feel stupid,” don’t, because you’re in good company.
I’ve encountered several designs in my professional life that shoved the randomness into the info parameter, and it perplexed me because there was a perfectly good salt parameter right there. It turned out, I was wrong to believe that, for all of the subtle and previously poorly documented reasons discussed above. But now we both know, and we’re all better off for it.
So don’t feel dumb for not knowing. I didn’t either, until this was pointed out to me by a very patient colleague.

(Art: LvJ)
Also, someone should really get NIST to be consistent about whether you should use HKDF or “KDF in Counter Mode with HMAC” as a PRF, because SP 800-108’s new revision doesn’t concede this point at all (presumably a relic from the 2009 draft).
This concession was made separately in 2011 with SP 800-56C revision 1 (presumably in response to criticism from the 2010 HKDF paper), and the present inconsistency is somewhat vexing.
(On that note, does anyone actually use the NIST 800-108 KDFs instead of HKDF? If so, why? Please don’t say you need CMAC…)
Bonus Content
These questions were asked after this blog post initially went public, and I thought they were worth adding. If you ask a good question, it may end up being edited in at the end, too.

Why Does HKDF use the Salt as the HMAC key in the Extract Step? (via r/crypto)
Broadly speaking, when applying a PRF to two “keys”, you get to decide which one you treat as the “key” in the underlying API.
HMAC’s API is HMACalg(key, message), but how HKDF uses it might as well be HMACalg(key1, key2).
The difference here seems almost arbitrary, but there’s a catch.
HKDF was designed for Diffie-Hellman outputs (before ECDH was the norm), which are generally able to be much larger than the block size of the underlying hash function. 2048-bit DH results fit in 256 bytes, which is 4 times the SHA256 block size.
If you have to make a decision, using the longer input (DH output) as the message is more intuitive for analysis than using it as the key, due to pre-hashing. I’ve discussed the counter-intuitive nature of HMAC’s pre-hashing behavior at length in this post, if you’re interested.
So with ECDH, it literally doesn’t matter which one was used (unless you have a weird mismatch in hash functions and ECC groups; i.e. NIST P-521 with SHA-224).
But before the era of ECDH, it was important to use the salt as the HMAC key in the extract step, since they were necessarily smaller than a DH group element.
Thus, HKDF chose HMACalg(salt, IKM) instead of HMACalg(IKM, salt) for the calculation of PRK in the HKDF-Extract step.
Neil Madden also adds that the reverse would create a chicken-egg situation, but I personally suspect that the pre-hashing would be more harmful to the security analysis than merely supplying a non-uniformly random bit string as an HMAC key in this specific context.
My reason for believing this is, when a salt isn’t supplied, it defaults to a string of 0x00 bytes as long as the output size of the underlying hash function. If the uniform randomness of the salt mattered that much, this wouldn’t be a tolerable condition.
https://soatok.blog/2021/11/17/understanding-hkdf/
#cryptographicHashFunction #cryptography #hashFunction #HMAC #KDF #keyDerivationFunction #securityDefinition #SecurityGuidance
As we look upon the sunset of a remarkably tiresome year, I thought it would be appropriate to talk about cryptographic wear-out.What is cryptographic wear-out?
It’s the threshold when you’ve used the same key to encrypt so much data that you should probably switch to a new key before you encrypt any more. Otherwise, you might let someone capable of observing all your encrypted data perform interesting attacks that compromise the security of the data you’ve encrypted.
My definitions always aim to be more understandable than pedantically correct.
(Art by Swizz)The exact value of the threshold varies depending on how exactly you’re encrypting data (n.b. AEAD modes, block ciphers + cipher modes, etc. each have different wear-out thresholds due to their composition).
Let’s take a look at the wear-out limits of the more popular symmetric encryption methods, and calculate those limits ourselves.
Specific Ciphers and Modes
(Art by Khia. Poorly edited by the author.)
Cryptographic Limits for AES-GCM
I’ve written about AES-GCM before (and why I think it sucks).AES-GCM is a construction that combines AES-CTR with an authenticator called GMAC, whose consumption of nonces looks something like this:
- Calculating H (used in GHASH for all messages encrypted under the same key, regardless of nonce):
Encrypt(00000000 00000000 00000000 00000000)
- Calculating J0 (the pre-counter block):
- If the nonce is 96 bits long:
NNNNNNNN NNNNNNNN NNNNNNNN 00000001where theNspaces represent the nonce hexits.
- Otherwise:
s = 128 * ceil(len(nonce)/nonce) - len(nonce)
J0 = GHASH(H, nonce || zero(s+64) || int2bytes(len(nonce))
- Each block of data encrypted uses J0 + block counter (starting at 1) as a CTR nonce.
- J0 is additionally used as the nonce to calculate the final GMAC tag.
AES-GCM is one of the algorithms where it’s easy to separately calculate the safety limits per message (i.e. for a given nonce and key), as well as for all messages under a key.
AES-GCM Single Message Length Limits
In the simplest case (nonce is 96 bits), you end up with the following nonces consumed:
- For each key:
00000000 00000000 00000000 00000000- For each (nonce, key) pair:
NNNNNNNN NNNNNNNN NNNNNNNN 000000001for J0NNNNNNNN NNNNNNNN NNNNNNNN 000000002for encrypting the first 16 bytes of plaintextNNNNNNNN NNNNNNNN NNNNNNNN 000000003for the next 16 bytes of plaintext…- …
NNNNNNNN NNNNNNNN NNNNNNNN FFFFFFFFFfor the final 16 bytes of plaintext.
From here, it’s pretty easy to see that you can encrypt the blocks from
00000002toFFFFFFFFwithout overflowing and creating a nonce reuse. This means that each (key, nonce) can be used to encrypt a single message up toblocks of the underlying ciphertext.
Since the block size of AES is 16 bytes, this means the maximum length of a single AES-GCM (key, nonce) pair is
bytes (or 68,719,476,480 bytes). This is approximately 68 GB or 64 GiB.
Things get a bit tricker to analyze when the nonce is not 96 bits, since it’s hashed.
The disadvantage of this hashing behavior is that it’s possible for two different nonces to produce overlapping ranges of AES-CTR output, which makes the security analysis very difficult.
However, this hashed output is also hidden from network observers since they do not know the value of H. Without some method of reliably detecting when you have an overlapping range of hidden block counters, you can’t exploit this.
(If you want to live dangerously and motivate cryptanalysis research, mix 96-bit and non-96-bit nonces with the same key in a system that does something valuable.)
Multi-Message AES-GCM Key Wear-Out
Now that we’ve established the maximum length for a single message, how many messages you can safely encrypt under a given AES-GCM key depends entirely on how your nonce is selected.If you have a reliable counter, which is guaranteed to never repeat, and start it at 0 you can theoretically encrypt
messages safely. Hooray!
Hooray!
(Art by Swizz)You probably don’t have a reliable counter, especially in real-world settings (distributed systems, multi-threaded applications, virtual machines that might be snapshotted and restored, etc.).
Confound you, technical limitations!
(Art by Swizz)Additionally (thanks to 2adic for the expedient correction), you cannot safely encrypt more than
blocks with AES because the keystream blocks–as the output of a block cipher–cannot repeat.
Most systems that cannot guarantee unique incrementing nonces simply generate nonces with a cryptographically secure random number generator. This is a good idea, but no matter how high quality your random number generator is, random functions will produce collisions with a discrete probability.
If you have
possible values, you should expect a single collision(with 50% probability) after
(or
)samples. This is called the birthday bound.
However, 50% of a nonce reuse isn’t exactly a comfortable safety threshold for most systems (especially since nonce reuse will cause AES-GCM to become vulnerable to active attackers). 1 in 4 billion is a much more comfortable safety margin against nonce reuse via collisions than 1 in 2. Fortunately, you can calculate the discrete probability of a birthday collision pretty easily.
If you want to rekey after your collision probability exceeds
(for a random nonce between 0 and
), you simply need to re-key after
messages.
AES-GCM Safety Limits
- Maximum message length:
bytes
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
(but you probably don’t have this luxury in the real world)
- Maximum data safely encrypted under a single key with a random nonce: about
bytes
Not bad, but we can do better.
(Art by Khia.)Cryptographic Limits for ChaCha20-Poly1305
The IETF version of ChaCha20-Poly1305 uses 96-bit nonces and 32-bit internal counters. A similar analysis follows from AES-GCM’s, with a few notable exceptions.For starters, the one-time Poly1305 key is derived from the first 32 bytes of the ChaCha20 keystream output (block 0) for a given (nonce, key) pair. There is no equivalent to AES-GCM’s H parameter which is static for each key. (The ChaCha20 encryption begins using block 1.)
Additionally, each block for ChaCha20 is 512 bits, unlike AES’s 128 bits. So the message limit here is a little more forgiving.
Since the block size is 512 bits (or 64 bytes), and only one block is consumed for Poly1305 key derivation, we can calculate a message length limit of
, or 274,877,906,880 bytes–nearly 256 GiB for each (nonce, key) pair.
The same rules for handling 96-bit nonces applies as with AES-GCM, so we can carry that value forward.
ChaCha20-Poly1305 Safety Limits
- Maximum message length:
bytes
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
(but you probably don’t have this luxury in the real world)
- Maximum data safely encrypted under a single key with a random nonce: about
bytes
A significant improvement, but still practically limited.
(Art by Khia.)Cryptographic Limits for XChaCha20-Poly1305
XChaCha20-Poly1305 is a variant of XSalsa20-Poly1305 (as used in libsodium) and the IETF’s ChaCha20-Poly1305 construction. It features 192-bit nonces and 32-bit internal counters.XChaCha20-Poly1305 is instantiated by using HChaCha20 of the key over the first 128 bits of the nonce to produce a subkey, which is used with the remaining nonce bits using the aforementioned ChaCha20-Poly1305.
This doesn’t change the maximum message length,but it does change the number of messages you can safely encrypt (since you’re actually using up todistinct keys).
Thus, even if you manage to repeat the final ChaCha20-Poly1305 nonce, as long as the total nonce differs, each encryptions will be performed with a distinct key (thanks to the HChaCha20 key derivation; see the XSalsa20 paper and IETF RFC draft for details).
UPDATE (2021-04-15): It turns out, my read of the libsodium implementation was erroneous due to endian-ness. The maximum message length for XChaCha20-Poly1305 is
blocks, and for AEAD_XChaCha20_Poly1305 is
blocks. Each block is 64 bytes, so that changes the maximum message length to about
. This doesn’t change the extended-nonce details, just the underlying ChaCha usage.
XChaCha20-Poly1305 Safety Limits
- Maximum message length:
bytes (earlier version of this document said
)- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
(but you probably don’t have this luxury in the real world)
- Maximum data safely encrypted under a single key with a random nonce: about
bytes
I can
seeencrypt forever, man.
(Art by Khia.)Cryptographic Limits for AES-CBC
It’s tempting to compare non-AEAD constructions and block cipher modes such as CBC (Cipher Block Chaining), but they’re totally different monsters.
- AEAD ciphers have a clean delineation between message length limit and the message quantity limit
- CBC and other cipher modes do not have this separation
Every time you encrypt a block with AES-CBC, you are depleting from a universal bucket that affects the birthday bound security of encrypting more messages under that key. (And unlike AES-GCM with long nonces, AES-CBC’s IV is public.)
This is in addition to the operational requirements of AES-CBC (plaintext padding, initialization vectors that never repeat and must be unpredictable, separate message authentication since CBC doesn’t provide integrity and is vulnerable to chosen-ciphertext atacks, etc.).
My canned response to most queries about AES-CBC.
(Art by Khia.)For this reason, most cryptographers don’t even bother calculating the safety limit for AES-CBC in the same breath as discussing AES-GCM. And they’re right to do so!
If you find yourself using AES-CBC (or AES-CTR, for that matter), you’d best be performing a separate HMAC-SHA256 over the ciphertext (and verifying this HMAC with a secure comparison function before decrypting). Additionally, you should consider using an extended nonce construction to split one-time encryption and authentication keys.
(Art by Riley.)
However, for the sake of completeness, let’s figure out what our practical limits are.
CBC operates on entire blocks of plaintext, whether you need the entire block or not.
On encryption, the output of the previous block is mixed (using XOR) with the current block, then encrypted with the block cipher. For the first block, the IV is used in the place of a “previous” block. (Hence, its requirements to be non-repeating and unpredictable.)
This means you can informally model (IV xor PlaintextBlock) and (PBn xor PBn+1) as a pseudo-random function, before it’s encrypted with the block cipher.
If those words don’t mean anything to you, here’s the kicker: You can use the above discussion about birthday bounds to calculate the upper safety bounds for the total number of blocks encrypted under a single AES key (assuming IVs are generated from a secure random source).
If you’re okay with a 50% probability of a collision, you should re-key after
blocks have been encrypted.
https://www.youtube.com/watch?v=v0IsYNDMV7A
If your safety margin is closer to the 1 in 4 billion (as with AES-GCM), you want to rekey after
blocks.
However, blocks encrypted doesn’t map neatly to bytes encrypted.
If your plaintext is always an even multiple of 128 bits (or 16 bytes), this allows for up to
bytes of plaintext. If you’re using PKCS#7 padding, keep in mind that this will include an entire padding block per message, so your safety margin will deplete a bit faster (depending on how many individual messages you encrypt, and therefore how many padding blocks you need).
On the other extreme (1-byte plaintexts), you’ll only be able to eek
encrypted bytes before you should re-key.
Therefore, to stay within the safety margin of AES-CBC, you SHOULD re-key after
blocks (including padding) have been encrypted.
Keep in mind:
single-byte blocks is still approximately 281 TiB of data (including padding). On the upper end,
15-byte blocks (with 1-byte padding to stay within a block) clocks in at about
or about 4.22 PiB of data.
That’s Blocks. What About Bytes?
The actual plaintext byte limit sans padding is a bit fuzzy and context-dependent.The local extrema occurs if your plaintext is always 16 bytes (and thus requires an extra 16 bytes of padding). Any less, and the padding fits within one block. Any more, and the data😛adding ratio starts to dominate.
Therefore, the worst case scenario with padding is that you take the above safety limit for block counts, and cut it in half. Cutting a number in half means reducing the exponent by 1.
But this still doesn’t eliminate the variance.
blocks could be anywhere from
to
bytes of real plaintext. When in situations like this, we have to assume the worst (n.b. take the most conservative value).
Therefore…
AES-CBC Safety Limits
- Maximum data safely encrypted under a single key with a random nonce:
bytes (approximately 141 TiB)
Yet another reason to dislike non-AEAD ciphers.
(Art by Khia.)Take-Away
Compared to AES-CBC, AES-GCM gives you approximately a million times as much usage out of the same key, for the same threat profile.ChaCha20-Poly1305 and XChaCha20-Poly1305 provides even greater allowances of encrypting data under the same key. The latter is even safe to use to encrypt arbitrarily large volumes of data under a single key without having to worry about ever practically hitting the birthday bound.
I’m aware that this blog post could have simply been a comparison table and a few footnotes (or even an IETF RFC draft), but I thought it would be more fun to explain how these values are derived from the cipher constructions.
(Art by Khia.)
https://soatok.blog/2020/12/24/cryptographic-wear-out-for-symmetric-encryption/
#AES #AESCBC #AESGCM #birthdayAttack #birthdayBound #cryptography #safetyMargin #SecurityGuidance #symmetricCryptography #symmetricEncryption #wearOut

Imagine you’re a software developer, and you need to authenticate users based on a username and password.
If you’re well-read on the industry standard best practices, you’ll probably elect to use something like bcrypt, scrypt, Argon2id, or PBKDF2. (If you thought to use something else, you’re almost certainly doing it wrong.)
Let’s say, due to technical constraints, that you’re forced to select PBKDF2 out of the above options, but you’re able to use a suitable hash function (i.e. SHA-256 or SHA-512, instead of SHA-1).
Every password is hashed with a unique 256-bit salt, generated from a secure random generator, and has an iteration count in excess of 80,000 (for SHA-512) or 100,000 (for SHA-256). So far, so good.

Let’s also say your users’ passwords are long, randomly-generated strings. This can mean either you’re building a community of password manager aficionados, or your users are actually software bots with API keys.
Every user’s password is, therefore, always a 256 character string of random hexadecimal characters.
Two sprints before your big launch, your boss calls you and says, “Due to arcane legal compliance reasons, we need to be able to detect duplicate passwords. It needs to be fast.”
You might might think, “That sounds like a hard problem to solve.”
Your boss insists, “The passwords are all too long and too high-entropy to reliably attacked, even when we’re using a fast hash, so we should be able to get by with a simple hash function for deduplication purposes.”
So you change your code to look like this:
<?phpuse ParagonIE\EasyDB\EasyDB;use MyApp\Security\PasswordHash;class Authentication { private EasyDB $db; public function __construct(EasyDB $db) { $this->db = $db; $this->pwhash = new PasswordHash('sha256'); } public function signUp(string $username, string $password) { // New: $hashed = hash('sha256', $password); if ($db->exists( "SELECT count(id) FROM users WHERE pw_dedupe = ?", $hashed )) { throw new Exception( "You cannot use the same username or password as another user." ); } // Original: if ($db->exists( "SELECT count(id) FROM users WHERE username = ?", $username )) { throw new Exception( "You cannot use the same username or password as another user." ); } $this->db->insert('users', [ 'username' => $username, 'pwhash' => $this->pwhash->hash($password), // Also new: 'pw_dedupe' => $hashed ]); } public function logIn(string $username, string $password): int { // This is unchanged: $user = $this->db->row("SELECT * FROM users WHERE username = ?", $username); if (empty($user)) { throw new Exception("Security Error: No user"); } if ($this->pwhash->verify($password, $user['pwhash'])) { throw new Exception("Security Error: Incorrect password"); } return (int) $user['id']; }}
Surely, this won’t completely undermine the security of the password hashing algorithm?

Three years later, a bored hacker discovers a read-only SQL injection vulnerability, and is immediately able to impersonate any user in your application.
What could have possibly gone wrong?
Cryptography Bugs Are Subtle
https://twitter.com/SwiftOnSecurity/status/832058185049579524
In order to understand what went wrong in our hypothetical scenario, you have to kinda know what’s under the hood in the monstrosity that our hypothetical developer slapped together.
PBKDF2
PBKDF2 stands for Password-Based Key Derivation Function #2. If you’re wondering where PBKDF1 went, I discussed its vulnerability in another blog post about the fun we can have with hash functions.
PBKDF2 is supposed to be instantiated with some kind of pseudo-random function, but it’s almost always HMAC with some hash function (SHA-1, SHA-256, and SHA-512 are common).
So let’s take a look at HMAC.
HMAC
HMAC is a Message Authentication Code algorithm based on Hash functions. Its definition looks like this:
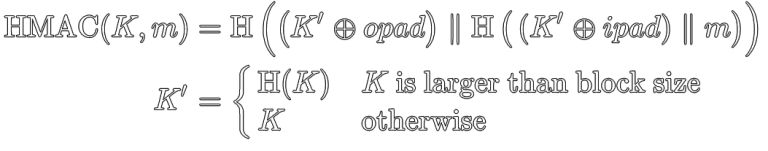
For the purposes of this discussion, we only care about the definition of K’.
If your key (K) is larger than the block size of the hash function, it gets pre-hashed with that hash function. If it’s less than or equal to the block size of the hash function, it doesn’t.
So, what is PBKDF2 doing with K?
How PBKDF2 Uses HMAC
The RFCs that define PBKDF2 aren’t super helpful here, but one needs only look at a reference implementation to see what’s happening.
// first iteration$last = $xorsum = hash_hmac($algorithm, $last, $password, true);// perform the other $count - 1 iterationsfor ($j = 1; $j < $count; $j++) {$xorsum ^= ($last = hash_hmac($algorithm, $last, $password, true));}$output .= $xorsum;
If you aren’t fluent in PHP, it’s using the previous round’s output as the message (m in the HMAC definition) and the password as the key (K).
Which means if your password is larger than the block size of the hash function used by HMAC (which is used by PBKDF2 under the hood), it will be pre-hashed.
The Dumbest Exploit Code
Okay, with all of that in mind, here’s how you can bypass the authentication of the above login script.
$httpClient->loginAs( $user['username'], hex2bin($user['pw_dedupe']));
Since K’ = H(K) when Length(K) > BlockSize(H), you can just take the pre-calculated hash of the user’s password and use that as the password (although not hex-encoded), and it will validate. (Demo.)

(Art by Khia.)
Above, when HMAC defined K’, it included a variant in its definition. Adding variants to hash function is a dumb way to introduce the risk of collisions. (See also: Trivial Collisions in IOTA’s Kerl hash function.)
Also, some PBKDF2 implementations that mishandle the pre-hashing of K, which can lead to denial-of-service attacks. Fun stuff, right?
Some Dumb Yet Effective Mitigations
Here are a few ways the hypothetical developer could have narrowly avoided this security risk:
- Use a different hash function for PBKDF2 and the deduplication check.
- e.g. PBKDF2-SHA256 and SHA512 would be impervious
- Always pre-hashing the password before passing it to PBKDF2.
- Our exploit attempt will effectively be double-hashed, and will not succeed.
- Use HMAC instead of a bare hash for the deduplication. With a hard-coded, constant key.
- Prefix the password with a distinct domain separation constant in each usage.
- Truncate the hash function, treating it as a Bloom filter.
- Some or all of the above.
- Push back on implementing this stupid feature to begin with.
Subtle problems often (but not always) call for subtle solutions.
Password Security Advice, Revisited
One dumb mitigation technique I didn’t include above is, “Using passwords shorter than the block size of the hash function.” The information security industry almost unanimously agrees that longer passwords are better than short ones (assuming both have the same distribution of possible characters at each position in the string, and are chosen randomly).
But here, we have a clear-cut example where having a longer password actually decreased security by allowing a trivial authentication bypass. Passwords with a length less than or equal to the block size of the hash function would not be vulnerable to the attack.
For reference, if you ever wanted to implement this control (assuming ASCII characters, where 1 character = 1 byte):
- 64-character passwords would be the upper limit for MD5, SHA-1, SHA-224, and SHA-256.
- 128-character passwords would be the upper limit for SHA-384 and SHA-512.
- (Since the above example used 256-character passwords, it always overflows.)
But really, one of the other mitigation techniques would be better. Limiting the input length is just a band-aid.
Another Non-Obvious Footgun
Converse to the block size of the hash function, the output size of the hash function also affects the security of PBKDF2, because each output is calculated sequentially. If you request more bytes out of a PBKDF2 function than the hash function outputs, it will have to work at least twice as hard.
This means that, while a legitimate user has to calculate the entire byte stream from PBKDF2, an attacker can just target the first N bytes (20 for SHA-1, 32 for SHA-256, 64 for SHA-512) of the raw hash output and attack that instead of doing all the work.
Is Cryptography Hard?
I’ve fielded a lot of questions in the past few weeks, and consequently overheard commentary from folks insisting that cryptography is a hard discipline and therefore only the smartest should study it. I disagree with that, but not for the reason that most will expect.
Many of the people reading this page will tell me, “This is such a dumb and obvious design flaw. Nobody would ship that code in production,” because they’re clever or informed enough to avoid disaster.
Yet, we still regularly hear about JWT alg=none vulnerabilities. And Johnny still still can’t encrypt. So cryptography surely can’t be easy.

Real-world cryptographic work is cognitively demanding. It becomes increasingly mathematically intensive the deeper you study, and nobody knows how to name things that non-cryptographers can understand. (Does anyone intuitively understand what a public key is outside of our field?)
In my opinion, cryptography is certainly challenging and widely misunderstood. There are a lot of subtle ways for secure building blocks to be stitched together insecurely. And today, it’s certainly a hard subject for most people to learn.
However, I don’t think its hardness is unavoidable.
Descending the Mohs Scale
There is a lot of gatekeeping in the information security community. (Maybe we should expect that to happen when people spend too many hours staring at firewall rules?)
“Don’t roll your own crypto” is something you hear a lot more often from software engineers and network security professionals than bona fide cryptographers.
Needless gatekeeping does the cryptographic community a severe disservice. I’m not the first to suggest that, either.
From what I’ve seen, far too many people feel discouraged from learning about cryptography, thinking they aren’t smart enough for it. It would seem A Mathematician’s Lament has an echo.
If it can be said that cryptography is hard today, then that has more to do with incomplete documentation and substandard education resources available for free online than some inherent mystical quality of our discipline that only the christened few can ever hope to master.
Cryptographers and security engineers that work in cryptography need more developers to play in our sandbox. We need more usability experts to discuss improvements to our designs and protocols to make them harder to misuse. We also need science communication experts and a legal strategy to stop idiotic politicians from trying to foolishly ban encryption.
So if you’re reading my blog, wondering, “Will I ever be smart enough to understand this crap?” the answer is probably “Yes!” It might not be easy, but with any luck, it’ll be easier than it was for the forerunners in our field.

(Art by Khia.)
I have one request, though: If you’re thinking of learning cryptography, please blog about your journey (even if you’re not a furry). You may end up filling in a pothole that would otherwise have tripped someone else up.
https://soatok.blog/2020/11/27/the-subtle-hazards-of-real-world-cryptography/
#computerSecurity #cryptographicHashFunction #cryptography #dumbExploit #HMAC #infosec #passwordHashing #PBKDF2 #SecurityGuidance
There are several different methods for securely hashing a password server-side for storage and future authentication. The most common one (a.k.a. the one that FIPS allows you to use, if compliance matters for you) is called PBKDF2. It stands for Password-Based Key Derivation Function #2.Why #2? It’s got nothing to do with pencils. There was, in fact, a PBKDF1! But PBKDF1 was fatally insecure in a way I find very interesting. This StackOverflow answer is a great explainer on the difference between the two.
Very Hand-Wavy Description of a Hash Function
Let’s defined a hash functionas any one-way transformation of some arbitrary-length string (
) to a fixed-length, deterministic, pseudo-random output.
Note: When in doubt, I err on the side of being easily understood by non-experts over pedantic precision. (Art by Swizz)
For example, this is a dumb hash function (uses SipHash-2-4 with a constant key):
function dumb_hash(string $arbitrary, bool $raw_binary = false): string{ $h = sodium_crypto_shorthash($arbitrary, 'SoatokDreamseekr'); if ($raw_binary) { return $h; } return sodium_bin2hex($h);}
You can see the output of this function with some sample inputs here.
Properties of Hash Functions
A hash function is considered secure if it has the following properties:
- Pre-image resistance. Given
, it should be difficult to find
.
- Second pre-image resistance. Given
, it should be difficult to find
such that
- Collision resistance. It should be difficult to find any arbitrary pair of messages (
) such that
That last property, collision resistance, is guaranteed up to the Birthday Bound of the hash function. For a hash function with a 256-bit output, you will expect to need on average
trial messages to find a collision.
If you’re confused about the difference between collision resistance and second pre-image resistance:
Collision resistance is about finding any two messages that produce the same hash, but you don’t care what the hash is as long as two distinct but known messages produce it.
On the other paw, second pre-image resistance is about finding a second message that produces a given hash.
Exploring PBKDF1’s Insecurity
If you recall, hash functions map an arbitrary-length string to a fixed-length string. If your input size is larger than your output size, collisions are inevitable (albeit computationally infeasible for hash functions such as SHA-256).But what if your input size is equal to your output size, because you’re taking the output of a hash function and feeding it directly back into the same hash function?
Then, as explained here, you get an depletion of the possible outputs with each successive iteration.
But what does that look like?
Without running the experiments on a given hash function, there are two possibilities that come to mind:
- Convergence. This is when
will, for two arbitrary messages and a sufficient number of iterations, converge on a single hash output.
- Cycles. This is when
for some integer
.
The most interesting result would be a quine, which is a cycle where
(that is to say,
).
The least interesting result would be for random inputs to converge into large cycles e.g. cycles of size
for a 256-bit hash function.
I calculated this lazily as the birthday bound of the birthday bound (so basically the 4th root, which foris
).
Update: According to this 1960 paper, the average time to cycle is
, and cycle length should be
, which means for a 256-bit hash you should expect a cycle after about
or about 128 bits, and the average cycle length will be about
. Thanks Riastradh for the corrections.
Conjecture: I would expect secure cryptographic hash functions in use today (e.g. SHA-256) to lean towards the least interesting output.
An Experiment Design
Since I don’t have an immense amount of cheap cloud computing at my disposal to run this experiments on a real hash function, I’m going to cheat a little and use my constant-key SipHash code from earlier in this post. In future work, cryptographers may find studying real hash functions (e.g. SHA-256) worthwhile.Given that SipHash is a keyed pseudo-random function with an output size of 64 bits, my dumb hash function can be treated as a 64-bit hash function.
This means that you should expect your first collision (with 50% probability) after only
trial hashes. This is cheap enough to try on a typical laptop.
Here’s a simple experiment for convergence:
- Generate two random strings
.
- Set
.
- Iterate
until
.
You can get the source code to run this trivial experiment here.
Clone the git repository, run
composer install, and thenphp bin/experiment.php. Note that this may need to run for a very long time before you get a result.If you get a result, you’ve found a convergence.
If the loop doesn’t terminate even after 2^64 iterations, you’ve definitely found a cycle. (Actually detecting a cycle and analyzing its length would require a lot of memory, and my simple PHP script isn’t suitable for this effort.)
“What do you mean I don’t have a petabyte of RAM at my disposal?”
What Does This Actually Tell Us?
The obvious lesson: Don’t design key derivation functions like PBKDF1.But beyond that, unless you can find a hash function that reliably converges or produces short cycles (
, for an n-bit hash function), not much. (This is just for fun, after all!)
Definitely fun to think about though! (Art by circuitslime)
If, however, a hash function is discovered to produce interesting results, this may indicate that the chosen hash function’s internal design is exploitable in some subtle ways that, upon further study, may lead to better cryptanalysis techniques. Especially if a hash quine is discovered.
(Header art by Khia)
https://soatok.blog/2020/05/05/putting-the-fun-in-hash-function/
#crypto #cryptography #hashFunction #SipHash

Earlier this year, Cendyne published A Deep Dive into Ed25519 Signatures, which covered some of the different types of digital signature algorithms, but mostly delved into the Ed25519 algorithm. Truth in advertising.
This got me thinking, “Why isn’t there a better comparison of different elliptic curve signature algorithms available online?”

Most people just defer to SafeCurves, but it’s a little dated: We have complete addition formulas for Weierstrass curves now, but SafeCurves doesn’t reflect that.
For the purpose of simplicity, I’m not going to focus on a general treatment of Elliptic Curve Cryptography (ECC), which includes pairing-based cryptography, Elliptic-Curve Diffie-Hellman, and (arguably) isogeny cryptography.
Instead, I’m going to focus entirely on elliptic curve digital signature algorithms.
Note: The content of this post is a bit lower-level than most programmers ever need to be concerned with. If you’re a programmer and interested in learning cryptography, start here. If you’re looking for library recommendations, libsodium is a good safe default.
Compliance Rules Everything Around Me
If you have to meet some arbitrary compliance requirements (i.e. FIPS 140-3, CNSA, etc.), your decision is already made for you, and you shouldn’t waste your time reading blogs like this that will only get your hopes up about the options available to you.
Choose the option your compliance officer demands, and hope it’s good enough.

Art: LvJ
Elliptic Curves for Signature Algorithms
Let’s start with the same curve Cendyne analyzed: Ed25519.
Ed25519 (EdDSA, Curve25519)
Ed25519 is one of the two digital signature algorithms today that use the EdDSA algorithm framework. The other is Ed448, which targets a higher security level (224-bit vs 128-bit) but is also slower and uses SHAKE256 (which is overkill and not great for performance).
Ed25519 is a safe default choice for most applications where a digital signature is appropriate, for many reasons:
- Ed25519 uses deterministic nonces, which means you’re severely unlikely to ever reproduce the Sony ECDSA k-reuse bug in your system.
The deterministic nonce is calculated from the SHA512 hash of the secret key and message. Two invocations tocrypto_sign_ed25519()with the same message and secret key will produce the same signature, but the intermediate nonce value is never revealed to an attacker. - Ed25519 includes the public key in the data hashed to produce the signature (more specifically s from the (R,s) pair). This offers a property that ECDSA lacks: Exclusive Ownership. I’ve written about this property before.
Without Exclusive Ownership, it’s possible to create a single signature value that’s valid for multiple different (message, public key) pairs.
Years ago, there would have an additional list item: Ed25519 uses Edward Curves, which have complete addition formulas and are therefore safer to implement in constant-time than Weierstrass curves (i.e. the NIST curves). However, we now have complete addition formulas for Weierstrass curves, so this has become a moot point (assuming your implementation uses complete addition formulas).
Ed25519 targets the 128-bit security level.
Why Not Use Ed25519?
There is one minor pitfall of Ed25519 that makes it unsuitable for esoteric uses (say, Ring Signature Schemes or zero-knowledge proofs): Ed25519 is not a prime-order group; it has a cofactor h = 8. This detail famously created a double-spend vulnerability in all CryptoNote-based cryptocurrencies (including Monero).
For systems that want the security of Ed25519 and its various well-studied implementations, but still need a prime-order group for their protocol, cryptographers have developed the Ristretto Group to meet your needs.
If you’re working on embedded systems, the determinism inherent to EdDSA might be undesirable due to the possibility of fault attacks. You can use a hedged variant of Ed25519 to mitigate this risk.
Additionally, Ed25519 is not approved for many government applications, although it did make the latest draft revision of FIPS 186 in 2019. If you care about compliance (see above), you cannot use Ed25519. Yet.

Guidance for Ed25519
Unless legally prohibited, Ed25519 should be your default choice, unless you need a prime-order group. In that case, build your desired protocol atop Ristretto255.
If you’re not sure if you need a prime-order group, you probably don’t. It’s a specialized requirement for uncommon use cases (ring signatures, password authenticated key exchange protocols, zero-knowledge proofs, etc.).

The Bitcoin Curve (ECDSA, secp256k1)
Secp256k1 is a Koblitz curve, which is a special case of Weierstrass curves that are more performant when used in binary fields, of the form, 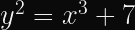
There is no specified reason why Bitcoin chose secp256k1 over another elliptic curve at the time of its inception, but we can speculate:
The author was a pseudonymous contributor to the Metzdowd mailing list for cypherpunks, and probably didn’t trust the NIST curves. Since Ed25519 didn’t exist at the time, the only obvious choice for a hipster elliptic curve parameter selection was to rely on the SECG recommendations, which specify the NIST and Koblitz curves. If you cross the NIST curves off the list, only the Koblitz curves remained.
Therefore, the selection of secp256k1 is likely an artefact of computer history and not a compelling reason to select secp256k1 in new designs. Please look elsewhere.

Secp256k1 targets the 128-bit security level.
Guidance for secp256k1
Don’t bother, there are better options. (i.e. Ed25519)
If you’re writing software for a cryptocurrency-related project, and you feel compelled to use secp256k1 for the sake of reducing your code footprint, please strongly consider the option of burning everything to the proverbial ground.

Art: Swizz
Cryptocurrency Aside, Why Avoid Secp256k1?
As we noted above, secp256k1 isn’t widely used outside of cryptocurrency.
As a direct consequence of this (as we’ll discuss in the NIST P-256 section), most cryptography libraries don’t offer optimized, side-channel-resistant implementations of secp256k1; even if they do offer optimized implementations of NIST P-256.
(Meanwhile, Ed25519 is designed to be side-channel and misuse-resistant, partly due to its Schnorr construction and constant-time ladder for scalar multiplication, so any library that implements Ed25519 is overwhelmingly likely to be constant-time.)
Therefore, any secp256k1 library for most programming languages that isn’t an FFI wrapper for libsecp256k1 will have worse performance than the other 256-bit curves.
https://twitter.com/bascule/status/1320183684935290882
Additionally, secp256k1 implementations are often a source of exploitable side-channels that permit attackers to pilfer your secret keys.
The previously linked article was about BouncyCastle’s implementation (which covers Java and .NET), but there’s still plenty of secp256k1 implementations that don’t FFI libsecp256k1.
From a quick Google Search:
- Python (uses EEA rather than Binary GCD for modular inverse)
- Go (uses Numbers, which weren’t designed for cryptography)
- PHP (uses GMP, which isn’t constant-time)
- JavaScript (calls here, which uses bn.js, which isn’t constant-time)
If you’re using secp256k1, and you’re not basing your choice on cybercash-interop, you’re playing with fire at the implementation and ecosystem levels–even if there are no security problems with the Koblitz curve itself.
You are much better off choosing any different curve than secp256k1 if you don’t have a Bitcoin/Ethereum/etc. interoperability requirement.

Art: LvJ
NIST P-256 (ECDSA, secp256r1)
NIST P-256 is the go-to curve to use with ECDSA in the modern era. Unlike Ed25519, P-256 uses a prime-order group, and is an approved algorithm to use in FIPS-validated modules.
Most cryptography libraries offer optimized assembly implementations of NIST P-256, which makes it less likely that your signing operations will leak timing information or become a significant performance bottleneck.
P-256 targets the 128-bit security level.
Why Not Use P-256?
Once upon a time, P-256 was riskier than Ed25519 (for signatures) and X25519 (for Diffie-Hellman), due to the incomplete addition formulas that led to timing-leaky implementations.
If you’re running old software, you may still be vulnerable to timing attacks that can recover your ECDSA secret key. However, there is a good chance that you’re on a modern and secure implementation in 2022, especially if you’re outsourcing this to OpenSSL or its derivatives.
ECDSA requires a secure randomness source to sign data. If you don’t have one available, and you sign anything, you’re coughing up your secret key to any attacker capable of observing multiple signatures.
Guidance for P-256
P-256 is an acceptable choice, especially if you’re forced to cope with FIPS and/or the CNSA suite requirements when using cryptography.
Of course, if you can get away with Ed25519, use Ed25519 instead.
If you use P-256, make sure you’re using it with SHA-256. Some implementations may default to something weaker (e.g. SHA-1).
If you’re also going to be performing ECDH with P-256, make sure you use compressed points. There used to be a patent; it died in 2018.
If you can afford it, make sure you use deterministic ECDSA (RFC 6979) or hedged signatures (if fault attacks are relevant to your threat model).

NIST P-384 (ECDSA, secp384r1)
NIST P-384 has a larger field than the curves we’ve previously examined, which allows P-384 to target the 192-bit security level. That’s the primary reason why anyone would choose P-384.
Naturally, elliptic curve security is more complicated than merely security against the Elliptic Curve Discrete Logarithm Problem (ECDLP).
P-384 is most often paired with SHA-384, which is the most widely used flavor of the SHA-2 family hash functions that isn’t susceptible to length-extension attacks. (There are also truncated SHA-512 variants specified later, but that’s also what SHA-384 is under-the-hood.)
If you’re aiming to build a “secure-by-default” tool for a system that the US government might one day become a customer of, with minimal cryptographic primitive choice, using NIST P-384 with SHA-384 makes for a reasonably minimalistic bundle.
Why Not Use P-384?
Unlike P-256, most P-384 implementations don’t use constant-time, optimized, and/or formally verified assembly code. (Notable counter-examples: AWS-LC and Go x/crypto.)
Like P-256, P-384 also requires a secure randomness source to sign data. If you aren’t providing one, expect your signing key to end up on fail0verflow one day.
Guidance for P-384
If you use P-384, make sure you’re using it with SHA-384.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

NIST P-521 (ECDSA, secp521r1)
Biggest curve is best curve! — the clueless
https://www.youtube.com/watch?v=i_APoSfCYwU
Systems that choose P-521 often have an interesting threat model, even though said threat model is rarely formally specified.
It’s overwhelmingly likely that what eventually breaks the 256-bit elliptic curves will also break P-521 in short order: Cryptography Relevant Quantum Computers.
The only thing P-521 does against CRQCs that P-256 doesn’t is require more quantum memory. If you’re worried about QRQCs, you might want to look into hybrid post-quantum signature schemes.
If you’re choosing P-521 in your designs, you’re basically saying, “I want to have 256 bits of asymmetric cryptographic security, come hell or high water!” even though the 128-bit security level is likely just fine for your actual threats.
Aside: P-521 and 512-bit ECC Security
P-521 is not a typo, although people sometimes think it is. P-521 uses the Mersenne prime 
This has led to an unfortunate trend in cryptography media to map ECC key sizes to symmetric security levels that misleads people as to the relationship between the two. For example:
Regrettably, this is misleading, because plotting the ECC Key Size versus equivalent Symmetric Security isn’t a how ECDLP security works. The ratio of the exponents involved is totally linear; it doesn’t suddenly increase beyond 384-bit curves for a mysterious mathematical reason.
- 256-bit Curves target the 128-bit security level
- 384-bit Curves target the 192-bit security level
- 512-bit Curves target the 256-bit security level
- 521-bit Curves actually target the 260-bit security level, but that meets or exceeds the 256-bit security level, so that’s how the standards are interpreted
The reason for this boils down entirely to the best attack against the Elliptic Curve Discrete Logarithm Problem: Pollard’s Rho, which recovers the secret key from an 
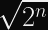
Taking the square root of a number is the same as halving its exponent, so the security level is half: 
Takeaway: If someone tells you that you need a 521-bit curve to meet the 256-bit security level, they are mistaken and it’s not their fault.

Why Not Use P-521?
It’s slow. Much slower than P-256 and Ed25519. Modestly slower than P-384.
Unlike P-384, you’re less likely to find an optimized, constant-time P-521 implementation.
Guidance for P-521
First, make a concerted effort to figure out the motivation for P-521 in your designs. Chances are, someone is putting too much emphasis on the wrong things for security.
If you use P-521, make sure you’re using it with SHA-512.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

Ed448 (EdDSA, Curve448)
Ed448 is the P-521 of the Edwards curves: It mostly exists to give standards committees a psychological comfort for the unlikely event that 256-bit ECC is desperately broken but ECC larger than 384 bits is somehow still safe.
https://twitter.com/dchest/status/703017144053833728
The very concept of having multiple “security levels” for raw cryptography primitives is mostly an artefact of the historical military roots of cryptography, rather than a serious consideration in the modern world.
Unfortunately, this leads to implementations that prioritize runtime algorithm selection negotiation, which maximizes the risk of protocol-level vulnerabilities. See also: JWT.
Ed448 was specified to use SHAKE256, which is a needlessly conservative decision which leads to an unnecessary performance bottleneck.
Why Not Use Ed448?
Aside from the performance hit mentioned previously, there’s no compelling reason to avoid Ed448 that isn’t also true of either Ed25519 or P-384.
Guidance for Ed448
If you want more speed, go with Ed25519. In addition to being faster, Ed25519 is also very widely supported.
If you need a prime-order field, use Decaf with Ed448 or consider P-384.
The Brainpool Curves
The main motivation for the Brainpool curves is that the NIST curves were not generated in a “verifiable pseudo-random way”.
The only reasons you’d ever want to support the Brainpool curves include:
- You think the NIST curves are somehow backdoored by the NSA
- You don’t appreciate small attack surfaces in cryptography libraries
- The German government told you to (see: compliance)
Most of the advice for the NIST Curves at each security level can be copy/pasted for the Brainpool curves, with one important caveat:
When considering real-world implementations, Brainpool curves are more likely to use the general purpose Big Number procedures (which aren’t always constant-time), rather than optimized assembly code, than the NIST curves are.
Therefore, my general guidance for the Brainpool curves is simply:
- Proceed at your own peril
- Consider hiring a cryptography engineer to study the implementation you’re relying on, especially with regard to timing attacks

Art: LvJ
Re-Examining the SafeCurves Criteria
Here’s a 2022 refresh of the SafeCurves criteria for all of the curves considered by this blog post.
| SafeCurve Criteria | Relevance to the Curves Listed Above |
|---|---|
| Fields | All relevant curves satisfy the requirements |
| Equations | All relevant curves satisfy the requirements |
| Base Points | All relevant curves satisfy the requirements |
| Rho | All relevant curves satisfy the requirements |
| Transfers | All relevant curves satisfy the requirements |
| Discriminants | Only secp256k1 doesn’t satisfy the requirements (out of the curves listed in this blog post) |
| Rigidity | The NIST curves do not meet this requirement. If you care about whether or not the standards were manipulated to insert a backdoor, rigidity matters to you. Otherwise, it’s not a deal-breaker. |
| Ladders | While a Montgomery ladder is beneficial for speed and implementation security, it isn’t strictly speaking required. This is an icing-on-the-cake consideration. |
| Twists | The only curve listed above that doesn’t meet the requirement is the 256-bit Brainpool curve (brainpoolp256t1). |
| Completeness | All relevant curves satisfy the requirements, as of 2015. SafeCurves is out of date here. |
| Indistinguishability | All relevant curves satisfy the requirements, as of 2014. |
SafeCurves continues to be a useful resource, especially if you stray from the guidance on this page.
For example: You wouldn’t want to use pairing-friendly curves for general purpose ECC digital signatures, because they’re suitable for specialized problems. SafeCurves correctly recommends not using BN(2,254).
However, SafeCurves is showing its age in 2022. BN curves still end up in digital signature protocol standards even though BLS-12-381 is clearly a better choice.
The Internet would benefit greatly for an updated SafeCurves that focuses on newer elliptic curve algorithms.

TL;DR
Ed25519 is great. NIST P-256 and P-384 are okay (with caveats). Anything else is questionable, and their parameter selection should come with a clear justification.
https://soatok.blog/2022/05/19/guidance-for-choosing-an-elliptic-curve-signature-algorithm-in-2022/
#asymmetricCryptography #BrainpoolCurves #cryptography #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #ellipticCurveCryptography #P256 #P384 #P521 #secp256k1 #secp256r1 #secp384r1 #secp521r1 #SecurityGuidance
A question I get asked frequently is, “How did you learn cryptography?”I could certainly tell everyone my history as a self-taught programmer who discovered cryptography when, after my website for my indie game projects kept getting hacked, I was introduced to cryptographic hash functions… but I suspect the question folks want answered is, “How would you recommend I learn cryptography?” rather than my cautionary tale about poorly-implemented password hash being a gateway bug.
The Traditional Ways to Learn
There are two traditional ways to learn cryptography.If you want a book to augment your journey in either traditional path, I recommend Serious Cryptography by Jean-Philippe Aumasson.
Academic Cryptography
The traditional academic way to learn cryptography involves a lot of self-study about number theory, linear algebra, discrete mathematics, probability, permutations, and field theory.You’d typically start off with classical ciphers (Caesar, etc.) then work your way through the history of ciphers until you finally reach an introduction to the math underpinning RSA and Diffie-Hellman, and maybe taught about Schneier’s Law and cautioned to only use AES and SHA-2… and then you’re left to your own devices unless you pursue a degree in cryptography.
The end result of people carelessly exploring this path is a lot of designs like Telegram’s MTProto that do stupid things with exotic block cipher modes and misusing vanilla cryptographic hash functions as message authentication codes; often with textbook a.k.a. unpadded RSA, AES in ECB, CBC, or some rarely-used mode that the author had to write custom code to handle (using ECB mode under the hood), and (until recently) SHA-1.
People who decide to pursue cryptography as a serious academic discipline will not make these mistakes. They’re far too apt for the common mistakes. Instead, they run the risk of spending years involved in esoteric research about homomorphic encryption, cryptographic pairings, and other cool stuff that might not see real world deployment (outside of novel cryptocurrency hobby projects) for five or more years.
That is to say: Academia is a valid path to pursue, but it’s not for everyone.
If you want to explore this path, Cryptography I by Dan Boneh is a great starting point.
Security Industry-Driven Cryptography
The other traditional way to learn cryptography is to break existing cryptography implementations. This isn’t always as difficult as it may sound: Reverse engineering video games to defeat anti-cheat protections has led several of my friends into learning about cryptography.For security-minded folks, the best place to start is the CryptoPals challenges. Another alternative is CryptoHack.
There are also plenty of CTF events all year around, but they’re rarely a good cryptography learning exercise above what CryptoPals offers. (Though there are notable exceptions.)
A Practical Approach to Learning Cryptography
Art by Kyume.
If you’re coming from a computer programming background and want to learn cryptography, the traditional approaches carry the risk of Reasoning By Lego.
Instead, the approach I recommend is to start gaining experience with the safest, highest-level libraries and then slowly working your way down into the details.
This approach has two benefits:
- If you have to implement something while you’re still learning, your knowledge and experience is stilted towards “use something safe and secure” not “hack together something with Blowfish in ECB mode and MD5 because they’re familiar”.
- You can let your own curiosity guide your education rather than follow someone else’s study guide.
To illustrate what this looks like, here’s how a JavaScript developer might approach learning cryptography, starting from the most easy-mode library and drilling down into specifics.
Super Easy Mode: DholeCrypto
Disclaimer: This is my project.Dhole Crypto is an open source library, implemented in JavaScript and PHP and powered by libsodium, that tries to make security as easy as possible.
I designed Dhole Crypto for securing my own projects without increasing the cognitive load of anyone reviewing my code.
If you’re an experienced programmer, you should be able to successfully use Dhole Crypto in a Node.js/PHP project. If it does not come easy, that is a bug that should be fixed immediately.
Easy Mode: Libsodium
Using libsodium is slightly more involved than Dhole Crypto: Now you have to know what a nonce is, and take care to manage them carefully.Advantage: Your code will be faster than if you used Dhole Crypto.
Libsodium is still pretty easy. If you use this cheat sheet, you can implement something secure without much effort. If you deviate from the cheat sheet, pay careful attention to the documentation.
If you’re writing system software (i.e. programming in C), libsodium is an incredibly easy-to-use library.
Moderate Difficulty: Implementing Protocols
Let’s say you’re working on a project where libsodium is overkill, and you only need a few cryptography primitives and constructions (e.g. XChaCha20-Poly1305). A good example: In-browser JavaScript.Instead of forcing your users to download the entire Sodium library, you might opt to implement a compatible construction using JavaScript implementations of these primitives.
Since you have trusted implementations to test your construction against, this should be a comparatively low-risk effort (assuming the primitive implementations are also secure), but it’s not one that should be undertaken without all of the prior experience.
Note: At this stage you are not implementing the primitives, just using them.
Hard Difficulty: Designing Protocols and Constructions
Repeat after me: “I will not roll my own crypto before I’m ready.” Art by AtlasInu.
To distinguish: TLS and Noise are protocols. AES-GCM and XChaCha20-Poly1305 are constructions.
Once you’ve implemented protocols and constructions, the next step in your self-education is to design new ones.
Maybe you want to combine XChaCha20 with a MAC based on the BLAKE3 hash function, with some sort of SIV to make the whole shebang nonce-misuse resistant?
You wouldn’t want to dive headfirst into cryptography protocol/construction design without all of the prior experience.
Very Hard Mode: Implementing Cryptographic Primitives
It’s not so much that cryptography primitives are hard to implement. You could fit RC4 in a tweet before they raised the character limit to 280. (Don’t use RC4 though!)The hard part is that they’re hard to implement securely. See also: LadderLeak.
Usually when you get to this stage in your education, you will have also picked up one or both of the traditional paths to augment your understanding. If not, you really should.
Nightmare Mode: Designing Cryptography Primitives
A lot of people like to dive straight into this stage early in their education. This usually ends in tears.If you’ve mastered every step in my prescribed outline and pursued both of the traditional paths to the point that you have a novel published attack in a peer-reviewed journal (and mirrored on ePrint), then you’re probably ready for this stage.
Bonus: If you’re a furry and you become a cryptography expert, you can call yourself a cryptografur. If you had no other reason to learn cryptography, do it just for pun!
Header art by circuitslime.
https://soatok.blog/2020/06/10/how-to-learn-cryptography-as-a-programmer/
#cryptography #education #programming #Technology

Cryptographers and cryptography engineers love to talk about the latest attacks and how to mitigate them. LadderLeak breaks ECDSA with less than 1 bit of nonce leakage? Raccoon attack brings the Hidden Number attack to finite field Diffie-Hellman in TLS?
And while this sort of research is important and fun, most software developers have much bigger problems to contend with, when it comes to the cryptographic security of their products and services.
So let’s start by talking about Java cryptography.

Cryptography in Java
In Java, the way you’re supposed to encrypt data using symmetric cryptography is with the javax.crypto.Cipher class. So to encrypt with AES-GCM, you’d call Cipher.getInstance("AES/GCM/NoPadding") and use the resulting object to process your data. javax.crypto.Cipher can be used for a lot of ill-advised modes (including ECB mode) and ciphers (including DES).
Can you guess what class you’d use to encrypt data with RSA in Java?
https://www.youtube.com/watch?v=9nSQs0Gr9FA
That’s right! RSA goes in the Cipher.getInstance("RSA/ECB/OAEPWithSHA-256AndMGF1Padding") hole.
(Or, more likely, Cipher.getInstance("RSA/ECB/PKCS1Padding"), which is not great.)

Also, as a reminder: You don’t want to encrypt data with RSA directly. You want to encrypt symmetric keys with RSA, and then encrypt your actual data with those symmetric keys. Preferably using a KEM+DEM paradigm.
Fun anecdote: The naming of RSA/ECB/$padding is misleading because it doesn’t actually implement a sort of ECB mode. However, a few projects over the years missed that memo and decided to implement RSA-ECB so they could be “compatible” with what they thought Java did. That is: They broke long messages into equal sized chunks (237 bytes for 2048-bit RSA), encrypted them independently, and then concatenated the ciphertexts together.
But it doesn’t end there. AES-GCM explodes brilliantly if you ever reuse a nonce. Naturally, the Cipher class shifts all of this burden onto the unwitting developer that calls it, which results in a regurgitated mess that looks like this (from the Java documentation):
GCMParameterSpec s = ...; cipher.init(..., s); // If the GCM parameters were generated by the provider, it can // be retrieved by: // cipher.getParameters().getParameterSpec(GCMParameterSpec.class); cipher.updateAAD(...); // AAD cipher.update(...); // Multi-part update cipher.doFinal(...); // conclusion of operation // Use a different IV value for every encryption byte[] newIv = ...; s = new GCMParameterSpec(s.getTLen(), newIv); cipher.init(..., s); ...
If you fail to perform this kata perfectly, you’ll introduce a nonce reuse vulnerability into your application.
And if you look a little deeper, you’ll also learn that their software implementation of AES (which is used in any platform without hardware AES available–such as Android on older hardware) isn’t hardened against cache-timing attacks… although their GHASH implementation is (which implies cache-timing attacks are within their threat model). But that’s an implementation problem, not a design problem.
Kludgey, hard-to-use, easy-to-misuse. It doesn’t have to be this way.
Learning From PHP
In 2015, when PHP 7 was being discussed on their mailing list, someone had the brilliant idea of creating a simple, cross-platform, extension-independent interface for getting random bytes and integers.
This effort would become random_bytes() and random_int() in PHP 7. (If you want to see how messy things were before PHP 7, take a look at the appropriate polyfill library.)
However, the initial design for this feature sucked really badly. Imagine the following code snippet:
function makePassword(int $length = 20): string{ $password = ''; for ($i = 0; $i < $length; ++$i) { $password .= chr(random_int(33, 124)); } return $password;}
If your operating system’s random number generator failed (e.g. you’re in a chroot and cannot access /dev/urandom), then the random_int() call would have returned false.
Because of type shenanigans in earlier versions of PHP, chr(false) returns a NUL byte. (This is fixed since 7.4 when strict_types is enabled, but the latest version at the time was PHP 5.6.)
After a heated debate on both the Github issue tracker for PHP and the internal mailing lists, the PHP project did the right thing: It will throw an Exception if it cannot safely generate random data.
Exceptions are developer-friendly: If you do not catch the exception, it kills the script immediately. If you decide to catch them, you can handle them in whatever graceful way you prefer. (Pretty error pages are often better than a white page and HTTP 500 status code, after all.)

In version 7.2 of the PHP programming language, they also made another win: Libsodium was promoted as part of the PHP standard library.
However, this feature isn’t as good as it could be: It’s easy to mix up inputs to the libsodium API since it expects string arguments instead of dedicated types (X25519SecretKey vs X25519PublicKey). To address this, the open source community has provided PHP libraries that avoid this mistake.
(I bet you weren’t expecting to hear that PHP is doing better with cryptography than Java in 2021, but here we are!)

Towards Usable Cryptography Interfaces
How can we do better? At a minimum, we need to internalize Avi Douglen’s rule of usable security.
Security at the expense of usability comes at the expense of security.
I’d like to propose a set of tenets that cryptography libraries can use to self-evaluate the usability of their own designs and implementations. Keep in mind that these are tenets, not a checklist, so the spirit of the law means more than the literal narrowly-scoped interpretation.
1. Follow the Principle of Least Astonishment
Cryptography code should be boring, never astonishing.
For example: If you’re comparing cryptographic outputs, it should always be done in constant-time–even if timing leaks do not help attackers (i.e. in password hashing validation).
2. Provide High-Level Abstractions
For example: Sealed boxes.
Most developers don’t need to fiddle with RSA and AES to construct their own hybrid public-key encryption designs (as you’d need to with Java). What they really need is a simple way to say, “Encrypt this so that only the recipient can decrypt it, but not the sender.”
This requires talking to your users and figuring out what their needs are instead of just assuming you know best.
3. Logically Separate Algorithm Categories
Put simply: Asymmetric cryptography belongs in a different API than symmetric cryptography. A similar separation should probably exist for specialized algorithms (e.g. multi-party computation and Shamir Secret Sharing).
Java may have got this one horribly wrong, but they’re not alone. The JWE specification (RFC 7518) also allows you to encrypt keys with:
- RSA with PKCS#1 v1.5 padding (asymmetric encryption)
- RSA with OAEP padding (asymmetric encryption)
- ECDH (asymmetric key agreement)
- AES-GCM (symmetric encryption)
If your users aren’t using a high-level abstraction, at least give them separate APIs for different algorithm types. If nothing else, it saves your users from having to ever type RSA/ECB again.
N.b. this means we should also collectively stop using the simple sign and verify verbs for Symmetric Authentication (i.e. HMAC) when these verbs imply digital signature algorithms (which are inherently asymmetric). Qualified verbs (verify –> sign_verify, mac_verify) are okay here.
4. Use Type-Safe Interfaces
If you allow any arbitrary string or byte array to be passed as the key, IV, etc. in your cryptography library, someone will misuse it.
Instead, you should have dedicated {structs, classes, types} (select appropriate) for each different kind of cryptography key your library expects. These keys should also provide guarantees about their contents (i.e. an Aes256GcmKey is always 32 bytes).
5. Defaults Matter
If you instantiate a new SymmetricCipher class, its default state should be an authenticated mode; never ECB.
The default settings are the ones that 80% of real world users should be using, if not a higher percentage.
6. Reduce Cognitive Load
If you’re encrypting data, why should your users even need to know what a nonce is to use it safely?
You MAY allow an explicit nonce if it makes sense for their application, but if they don’t provide one, generate a random nonce and handle it for them.
Aside: There’s an argument that we should have a standard for committing, deterministic authenticated encryption. If you need non-determinism, stick a random 256-bit nonce in the AAD and you get that property too. I liked to call this combination AHEAD (Authenticated Hedged Encryption with Associated Data), in the same vein as Hedged Signatures.
The less choices a user has to make to get their code working correctly, the less likely they’ll accidentally introduce a subtle flaw that makes their application hideously insecure.
7. Don’t Fail at Failure
If what you’re doing is sensitive to error oracles (e.g. padding), you have to be very careful about how you fail.
For example: RSA decryption with PKCS#1v1.5 padding. Doing a constant-time swap between the actual plaintext and some random throwaway value so the decryption error can result from the symmetric decryption is better than aborting.
Conversely, if you’re depending on a component to generate randomness for you and it fails, it shouldn’t fail silently and return bad data.
Security is largely about understanding how systems fail, so there’s no one-size-fits-all answer for this. However, the exact failure mechanism for a cryptographic feature should be decided very thoughtfully.
8. Minimize Runtime Negotiation
This is more of a concern for applications than libraries, but it bears mentioning here: The algorithm you’re using shouldn’t be something an attacker can decide. It should be determined at compile-time, not at run-time.
For example: There were several vulnerabilities in JSON Web Tokens where you could swap out the alg header to none (which removed all security) or from RS256 (RSA signed) to HS256…which meant the RSA public key was being used as an HMAC symmetric key. (See tenet 4 above.)
Header art by Scruff Kerfluff.
https://soatok.blog/2021/02/24/cryptography-interface-design-is-a-security-concern/
#API #APIDesign #crypto #cryptography #cryptographyLibraries #SecurityGuidance
A paper was published on the IACR’s ePrint archive yesterday, titled LadderLeak: Breaking ECDSA With Less Than One Bit of Nonce Leakage.The ensuing discussion on /r/crypto led to several interesting questions that I thought would be worth capturing and answering in detail.
What’s Significant About the LadderLeak Paper?
This is best summarized by Table 1 from the paper.The sections labeled “This work” are what’s new/significant about this research.
The paper authors were able to optimize existing attacks exploiting one-bit leakages against 192-bit and 160-bit elliptic curves. They were further able to exploit leakages of less than one bit in the same curves.How Can You Leak Less Than One Bit?
We’re used to discrete quantities in computer science, but you can leak less than one bit of information in the case of side-channels.Biased modular reduction can also create a vulnerable scenario: If you know the probability of a 0 or a 1 in a given position in the bit-string of the one-time number (i.e. the most significant bit) is not 0.5 to 0.5, but some other ratio (e.g. 0.51 to 0.49), you can (over many samples) conclude a probability of a specific bit in your dataset.
If “less than one bit” sounds strange, that’s probably our fault for always rounding up to the nearest bit when we express costs in computer science.
What’s the Cost of the Attack?
Consult Table 3 from the paper for empirical cost data:Table 3 from the LadderLeak paper.
How Devastating is LadderLeak?
First, it assumes a lot of things:
- That you’re using ECDSA with either sect163r1 or secp192r1 (NIST P-192). Breaking larger curves requires more bits of bias (as far as we know).
- That you’re using a cryptography library with cache-timing leaks.
- That you have a way to measure the timing leaks (and not just pilfer the ECDSA secret key; i.e. in a TPM setup). This threat model generally assumes some sort of physical access.
But if you can pull the attack off, you can successfully recover the device’s ECDSA secret key. Which, for protocols like TLS, allow an attacker to impersonate a certificate-bearer (typically the server)… which is pretty devastating.
Is ECDSA Broken Now?
Non-deterministic ECDSA is not significantly more broken with LadderLeak than it already was by other attacks. LadderLeak does not break the Internet.Fundamentally, LadderLeak doesn’t really change the risk calculus. Bleichenbacher’s attack framework for solving the Hidden Number Problem using Lattices was already practical, with sufficient samples.
There’s even a CryptoPals challenge about these attacks.
As an acquaintance put it, the authors made a time-memory trade-off with a leaky oracle. It’s a neat result worthy of publication, but we aren’t any minutes closer to midnight with this revelation.
Is ECDSA’s k-value Really a Nonce?
Ehhhhhhhhh, sorta.
It’s complicated!
Nonce in cryptography has always meant “number that must be used only once” (typically per key). See: AES-GCM.
Nonces are often confused for initialization vectors (IVs), which in addition to a nonce’s requirements for non-reuse must also be unpredictable. See: AES-CBC.
However, nonces and IVs can both be public, whereas ECDSA k-values MUST NOT be public! If you recover the k-value for a given signature, you can recover the secret key too.
That is to say, ECDSA k-values must be all of the above:
- Never reused
- Unpredictable
- Secret
- Unbiased
They’re really in a class of their own.
For that reason, it’s probably better to think of the k-value as a per-signature key than a simple nonce. (n.b. Many cryptography libraries actually implement them as a one-time ECDSA keypair.)
What’s the Difference Between Random and Unpredictable?
The HMAC-SHA256 output of a message under a secret key is unpredictable for anyone not in possession of said secret key. This value, though unpredictable, is not random, since signing the same message twice yields the same output.A large random integer when subjected to modular reduction by a non-Mersenne prime of the same magnitude will be biased towards small values. This bias may be negligible, but it makes the bit string that represents the reduced integer more predictable, even though it’s random.
What Should We Do? How Should We Respond?
First, don’t panic. This is interesting research and its authors deserve to enjoy their moment, but the sky is not falling.Second, acknowledge that none of the attacks are effective against EdDSA.
If you feel the urge to do something about this attack paper, file a support ticket with all of your third-party vendors and business partners that handle cryptographic secrets to ask them if/when they plan to support EdDSA (especially if FIPS compliance is at all relevant to your work, since EdDSA is coming to FIPS 186-5).
Reason: With increased customer demand for EdDSA, more companies will adopt this digital signature algorithm (which is much more secure against real-world attacks). Thus, we can ensure an improved attack variant that actually breaks ECDSA doesn’t cause the sky to fall and the Internet to be doomed.
(Seriously, I don’t think most companies can overcome their inertia regarding ECDSA to EdDSA migration if their customers never ask for it.)
https://soatok.blog/2020/05/26/learning-from-ladderleak-is-ecdsa-broken/
#crypto #cryptography #digitalSignatureAlgorithm #ECDSA #ellipticCurveCryptography #LadderLeak

Let’s talk about digital signature algorithms.
Digital signature algorithms are one of the coolest ideas to come out of asymmetric (a.k.a. public-key) cryptography, but they’re so simple and straightforward that most cryptography nerds don’t spend a lot of time thinking about them.
Even though you are more likely to run into a digital signature as a building block (e.g. certificate signatures in TLS) than think about them in isolation (e.g. secure software releases), they’re still really cool and worth learning about.
What’s a Digital Signature?
A digital signature is some string that proves that a specific message was signed by some specific entity in possession of the secret half of an asymmetric key-pair. Digital Signature Algorithms define the process for securely signing and verifying messages with their associated signatures.
For example, if I have the following keypair:
- Secret key:
9080a2c7897faeb8526968161695da0f7b3afa2e8e7d8e8369a85547ab48ea05 - Public key:
482b8d3430445cdad6b5ce59778e09ab59d099120f32d316e881db1a6330390b
I can cryptographically sign the message “Dhole Moments: Never a dull moment!” with the above secret key, and it will generate the signature string: 63629779a31b623486145359c6f1d56602d8d9135e4b17fa2ae3667c8947397decd7ae01bfed08645a429f5dee906e87df4e18eefdfff9acb5b1488c9dec800f.
If you only have the message, signature string, and my public key, you can verify that I signed the message. But, very crucially, you cannot sign messages and convince someone else that they came from me. (With symmetric authentication schemes, such as HMAC, you can.)
A digital signature algorithm is considered secure if, in order for anyone else to pass off a different message as being signed by me, they would need my secret key to succeed. When this assumption holds true, we say the scheme is secure against existential forgery attacks.
How Do Digital Signatures Work?
Simple answer: They generally combine a cryptographic hash function (e.g. SHA-256) with some asymmetric operation, and the details beyond that are all magic.
More complicated answer: That depends entirely on the algorithm in question!

For example, with RSA signatures, you actually encrypt a hash of the message with your secret key to sign the message, and then you RSA-decrypt it with your public key to verify the signature. This is backwards from RSA encryption (where you do the totally sane thing: encrypt with public key, decrypt with secret key).
In contrast, with ECDSA signatures, you’re doing point arithmetic over an elliptic curve (with a per-signature random value).
Yet another class of digital signature algorithms are hash-based signatures, such as SPHINCS+ from the NIST Post-Quantum Cryptography Standardization effort, wherein your internals consist entirely of hash functions (and trees of hash functions, and stream ciphers built with other hash functions).
In all cases, the fundamental principle stays the same: You sign a message with a secret key, and can verify it with a public key.
In the interest of time, I’m not going to dive deep into how each signature algorithm works. That can be the subject of future blog posts (one for each of the algorithms in question).
Quick aside: Cryptographers who stumble across my blog might notice that I deviate from convention a bit. They typically refer to the sensitive half of an asymmetric key pair as a “private key”, but I instead call it a “secret key”.
The main reason for this is that “secret key” can be abbreviated as “sk” and public key can be abbreviated as “pk”, whereas private/public doesn’t share this convenience. If you ever come across their writings and wonder about this discrepancy, I’m breaking away from the norm and their way is more in line with the orthodoxy.
What Algorithms Should I Use?

If you find yourself asking this question, you’re probably dangerously close to rolling your own crypto. If so, you’ll want to hire a cryptographer to make sure your designs aren’t insecure. (It’s extremely easy to design or implement otherwise-secure cryptography in an insecure way.)
Recommended Digital Signature Algorithms
(Update, 2022-05-19): I’ve published a more in-depth treatment of the Elliptic Curve Digital Signature Algorithms a few years after this post was created. A lot of the topics covered by EdDSA and ECDSA are focused on there.
EdDSA: Edwards Curve DSA
EdDSA comes in two variants: Ed25519 (widely supported in a lot of libraries and protocols) and Ed448 (higher security level, but not implemented or supported in as many places).
The IETF standardized EdDSA in RFC 8032, in an effort related to the standardization of RFC 7748 (titled: Elliptic Curves for Security).
Formally, EdDSA is derived from Schnorr signatures and defined over Edwards curves. EdDSA’s design was motivated by the real-world security failures of ECDSA:
- Whereas ECDSA requires a per-signature secret number (
) to protect the secret key, EdDSA derives the per-signature nonce deterministically from a hash of the secret key and message.
- ECDSA with biased nonces can also leak your secret key through lattice attacks. To side-step this, EdDSA uses a hash function twice the size as the prime (i.e. SHA-512 for Ed25519), which guarantees that the distribution of the output of the modular reduction is unbiased (assuming uniform random inputs).
- ECDSA implemented over the NIST Curves is difficult to implement in constant-time: Complicated point arithmetic rules, point division, etc. EdDSA only uses operations that are easy to implement in constant-time.
For a real-world example of why EdDSA is better than ECDSA, look no further than the Minerva attacks, and the Ed25519 designer’s notes on why EdDSA stood up to the attacks.
The security benefits of EdDSA over ECDSA are so vast that FIPS 186-5 is going to include Ed25519 and Ed448.

This is kind of a big deal! The FIPS standards are notoriously slow-moving, and they’re deeply committed to a sunk cost fallacy on algorithms they previously deemed acceptable for real-world deployment.
RFC 6979: Deterministic ECDSA
Despite EdDSA being superior to ECDSA in virtually every way (performance, security, misuse-resistance), a lot of systems still require ECDSA support for the foreseeable future.
If ECDSA is here to stay, we might as well make it suck less in real-world deployments. And that’s exactly what Thomas Pornin did when he wrote RFC 6979: Deterministic Usage of DSA and ECDSA.
(Like EdDSA, Deterministic ECDSA is on its way to FIPS 186-5. Look for it in FIPS-compliant hardware 5 years from now when people actually bother to update their implementations.)
Acceptable Digital Signature Algorithms
ECDSA Signatures
The Elliptic Curve Digital Signature Algorithm (ECDSA) is the incumbent design for signatures. Unlike EdDSA, ECDSA is a more flexible design that has been applied to many different types of curves.
This is more of a curse than a blessing, as Microsoft discovered with CVE-2020-0601: You could take an existing (signature, public key) pair with standard curve, explicitly set the generator point equal to the victim’s public key, and set your secret key to 1, and Windows’s cryptography library would think, “This is fine.”
For this reason, cryptographers were generally wary of proposals to add support for Koblitz curves (including secp256k1–the Bitcoin curve) or Brainpool curves into protocols that are totally fine with NIST P-256 (and maybe NIST P-384 if you need it for compliance reasons).
For that reason, if you can’t use EdDSA or RFC 6979, your fallback option is ECDSA with one of those two curves (secp256r1, secp384r1), and making sure that you have access to a reliable cryptographic random number generator.
RSA Signatures
It’s high time the world stopped using RSA.
Not just for the reasons that Trail of Bits is arguing (which I happen to agree with), but more importantly:
Replacing RSA with EdDSA (or Deterministic ECDSA) also gives teams an opportunity to practice migrating from one cryptography algorithm suite to another, which will probably be a much-needed experience when quantum computers come along and we’re all forced to migrate to post-quantum cryptography.
Encryption is a bigger risk of being broken by quantum computers than signature schemes: If you encrypt data today, a quantum computer 20 years down the line can decrypt it immediately. Conversely, messages that are signed today cannot be broken until after a quantum computer exists.
That being said, if you only need signatures and not encryption, RSA is still acceptable. If you also need encryption, don’t use RSA for that purpose.
If you can, use PSS padding rather than PKCS#1 v1.5 padding, with SHA-256 or SHA-384. But for signatures (i.e. not encryption), PKCS#1 v1.5 padding is fine.
Dishonorable Mention
DSA Signatures
There’s really no point in using classical DSA, when ECDSA is widely supported and has more ongoing attention from cryptography experts.
If you’re designing a system in 2020 that uses DSA, my only question for you is…

Upcoming Signature Algorithms
Although it is far too early to consider adopting these yet, cryptographers are working on new designs that protect against wider ranges of real-world threats.
Let’s briefly look at some of them and speculate wildly about what the future looks like. For fun. Don’t use these yet, unless you have a very good reason to do so.
Digital Signature Research Topics
Hedged Signatures
Above, we concluded that EdDSA and Deterministic ECDSA were generally the best choice (and what I’d recommend for software developers). There is one important caveat: Fault attacks.
A fault attack is when you induce a hardware fault into a computer chip, and thereby interfere with the correct functioning of a cryptography algorithm. This is especially relevant to embedded devices and IoT.
The IETF’s CFRG is investigating the use of additional randomization of messages (rather than randomizing signatures) as a safeguard against leaking secret keys through fault injection.
Of course, the Dhole Cryptography Library (my libsodium wrapper for JavaScript and PHP) already provides a form of Hedged Signatures.
If this technique is proven successful at mitigating fault injection attacks, then libsodium users will be able to follow the technique outlined in Dhole Crypto to safeguard their own protocols against fault attacks. Until then, they’re at least as safe as deterministic EdDSA today.
Threshold ECDSA Signatures
Suppose you have a scenario where you want 3-or-more people to have to sign a message before it’s valid. That’s exactly what Threshold ECDSA with Fast Trustless Setup aspires to provide.
Although this is mostly being implemented in cryptocurrency projects today, the cryptography underpinnings are fascinating. At worst, this will be one good side-effect to come from blockchain mania.
Post-Quantum Digital Signatures
Hash-Based Signatures
The best hash-based signature schemes are based on the SPHINCS design for one simple reason: It’s stateless.
In earlier hash-based digital signatures, such as XMSS, you have to maintain a state of which keys you’ve already used, to prevent attacks. Google’s Adam Langley previously described this as a “huge foot-cannon” for security (although probably okay in some environments, such as an HSM).
Lattice-Based Signatures
There are a lot of post-quantum signature algorithm designs defined over lattice groups, but my favorite lattice-based design is called FALCON. FALCON stands for FAst-Fourier Lattice-based COmpact Signatures Over NTRU.
Sign Here, Please
Who knew there would be so much complexity involved with such a simple cryptographic operation? And we didn’t even dive deep on how any of them work.
That’s the problem with cryptography: It’s a fractal of complexity. The more you know about these topics, the deeper the complexity becomes.
But if you’re implementing a protocol today and need a digital signature algorithm, use (in order of preference):
- Ed25519 or Ed448
- ECDSA over NIST P-256 or P-384, with RFC 6979
- ECDSA over NIST P-256 or P-384, without RFC 6979
- RSA (as a last resort)
But most importantly: make sure you have a cryptographer audit your designs.
(Header art by Kyume.)
https://soatok.blog/2020/04/26/a-furrys-guide-to-digital-signature-algorithms/
#crypto #cryptography #DeterministicSignatures #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #FIPS #FIPS186 #FIPSCompliance #RFC6979 #SecurityGuidance
Earlier this year, Cendyne published A Deep Dive into Ed25519 Signatures, which covered some of the different types of digital signature algorithms, but mostly delved into the Ed25519 algorithm. Truth in advertising.This got me thinking, “Why isn’t there a better comparison of different elliptic curve signature algorithms available online?”
Art: LvJ
Most people just defer to SafeCurves, but it’s a little dated: We have complete addition formulas for Weierstrass curves now, but SafeCurves doesn’t reflect that.
For the purpose of simplicity, I’m not going to focus on a general treatment of Elliptic Curve Cryptography (ECC), which includes pairing-based cryptography, Elliptic-Curve Diffie-Hellman, and (arguably) isogeny cryptography.
Instead, I’m going to focus entirely on elliptic curve digital signature algorithms.
Note: The content of this post is a bit lower-level than most programmers ever need to be concerned with. If you’re a programmer and interested in learning cryptography, start here. If you’re looking for library recommendations, libsodium is a good safe default.
Compliance Rules Everything Around Me
If you have to meet some arbitrary compliance requirements (i.e. FIPS 140-3, CNSA, etc.), your decision is already made for you, and you shouldn’t waste your time reading blogs like this that will only get your hopes up about the options available to you.Choose the option your compliance officer demands, and hope it’s good enough.
“Sure, let me check that box.”
Art: LvJElliptic Curves for Signature Algorithms
Let’s start with the same curve Cendyne analyzed: Ed25519.Ed25519 (EdDSA, Curve25519)
Ed25519 is one of the two digital signature algorithms today that use the EdDSA algorithm framework. The other is Ed448, which targets a higher security level (224-bit vs 128-bit) but is also slower and uses SHAKE256 (which is overkill and not great for performance).Ed25519 is a safe default choice for most applications where a digital signature is appropriate, for many reasons:
- Ed25519 uses deterministic nonces, which means you’re severely unlikely to ever reproduce the Sony ECDSA k-reuse bug in your system.
The deterministic nonce is calculated from the SHA512 hash of the secret key and message. Two invocations tocrypto_sign_ed25519()with the same message and secret key will produce the same signature, but the intermediate nonce value is never revealed to an attacker.- Ed25519 includes the public key in the data hashed to produce the signature (more specifically s from the (R,s) pair). This offers a property that ECDSA lacks: Exclusive Ownership. I’ve written about this property before.
Without Exclusive Ownership, it’s possible to create a single signature value that’s valid for multiple different (message, public key) pairs.Years ago, there would have an additional list item: Ed25519 uses Edward Curves, which have complete addition formulas and are therefore safer to implement in constant-time than Weierstrass curves (i.e. the NIST curves). However, we now have complete addition formulas for Weierstrass curves, so this has become a moot point (assuming your implementation uses complete addition formulas).
Ed25519 targets the 128-bit security level.
Why Not Use Ed25519?
There is one minor pitfall of Ed25519 that makes it unsuitable for esoteric uses (say, Ring Signature Schemes or zero-knowledge proofs): Ed25519 is not a prime-order group; it has a cofactor h = 8. This detail famously created a double-spend vulnerability in all CryptoNote-based cryptocurrencies (including Monero).For systems that want the security of Ed25519 and its various well-studied implementations, but still need a prime-order group for their protocol, cryptographers have developed the Ristretto Group to meet your needs.
If you’re working on embedded systems, the determinism inherent to EdDSA might be undesirable due to the possibility of fault attacks. You can use a hedged variant of Ed25519 to mitigate this risk.
Additionally, Ed25519 is not approved for many government applications, although it did make the latest draft revision of FIPS 186 in 2019. If you care about compliance (see above), you cannot use Ed25519. Yet.
A niche Internet meme for cryptography engineers
Guidance for Ed25519
Unless legally prohibited, Ed25519 should be your default choice, unless you need a prime-order group. In that case, build your desired protocol atop Ristretto255.If you’re not sure if you need a prime-order group, you probably don’t. It’s a specialized requirement for uncommon use cases (ring signatures, password authenticated key exchange protocols, zero-knowledge proofs, etc.).
Art: LvJ
The Bitcoin Curve (ECDSA, secp256k1)
Secp256k1 is a Koblitz curve, which is a special case of Weierstrass curves that are more performant when used in binary fields, of the form,. This curve is almost exclusively used in cryptocurrency software.
There is no specified reason why Bitcoin chose secp256k1 over another elliptic curve at the time of its inception, but we can speculate:
The author was a pseudonymous contributor to the Metzdowd mailing list for cypherpunks, and probably didn’t trust the NIST curves. Since Ed25519 didn’t exist at the time, the only obvious choice for a hipster elliptic curve parameter selection was to rely on the SECG recommendations, which specify the NIST and Koblitz curves. If you cross the NIST curves off the list, only the Koblitz curves remained.
Therefore, the selection of secp256k1 is likely an artefact of computer history and not a compelling reason to select secp256k1 in new designs. Please look elsewhere.
Fact: Imgflip didn’t have a single secp256k1 meme until I made this one.
Secp256k1 targets the 128-bit security level.
Guidance for secp256k1
Don’t bother, there are better options. (i.e. Ed25519)If you’re writing software for a cryptocurrency-related project, and you feel compelled to use secp256k1 for the sake of reducing your code footprint, please strongly consider the option of burning everything to the proverbial ground.
Cryptocurrency sucks!
Art: SwizzCryptocurrency Aside, Why Avoid Secp256k1?
As we noted above, secp256k1 isn’t widely used outside of cryptocurrency.As a direct consequence of this (as we’ll discuss in the NIST P-256 section), most cryptography libraries don’t offer optimized, side-channel-resistant implementations of secp256k1; even if they do offer optimized implementations of NIST P-256.
(Meanwhile, Ed25519 is designed to be side-channel and misuse-resistant, partly due to its Schnorr construction and constant-time ladder for scalar multiplication, so any library that implements Ed25519 is overwhelmingly likely to be constant-time.)
Therefore, any secp256k1 library for most programming languages that isn’t an FFI wrapper for libsecp256k1 will have worse performance than the other 256-bit curves.
https://twitter.com/bascule/status/1320183684935290882
Additionally, secp256k1 implementations are often a source of exploitable side-channels that permit attackers to pilfer your secret keys.
The previously linked article was about BouncyCastle’s implementation (which covers Java and .NET), but there’s still plenty of secp256k1 implementations that don’t FFI libsecp256k1.
From a quick Google Search:
- Python (uses EEA rather than Binary GCD for modular inverse)
- Go (uses Numbers, which weren’t designed for cryptography)
- PHP (uses GMP, which isn’t constant-time)
- JavaScript (calls here, which uses bn.js, which isn’t constant-time)
If you’re using secp256k1, and you’re not basing your choice on cybercash-interop, you’re playing with fire at the implementation and ecosystem levels–even if there are no security problems with the Koblitz curve itself.
You are much better off choosing any different curve than secp256k1 if you don’t have a Bitcoin/Ethereum/etc. interoperability requirement.
“No thanks, I use Ed25519.”
Art: LvJNIST P-256 (ECDSA, secp256r1)
NIST P-256 is the go-to curve to use with ECDSA in the modern era. Unlike Ed25519, P-256 uses a prime-order group, and is an approved algorithm to use in FIPS-validated modules.Most cryptography libraries offer optimized assembly implementations of NIST P-256, which makes it less likely that your signing operations will leak timing information or become a significant performance bottleneck.
P-256 targets the 128-bit security level.
Why Not Use P-256?
Once upon a time, P-256 was riskier than Ed25519 (for signatures) and X25519 (for Diffie-Hellman), due to the incomplete addition formulas that led to timing-leaky implementations.If you’re running old software, you may still be vulnerable to timing attacks that can recover your ECDSA secret key. However, there is a good chance that you’re on a modern and secure implementation in 2022, especially if you’re outsourcing this to OpenSSL or its derivatives.
ECDSA requires a secure randomness source to sign data. If you don’t have one available, and you sign anything, you’re coughing up your secret key to any attacker capable of observing multiple signatures.
Guidance for P-256
P-256 is an acceptable choice, especially if you’re forced to cope with FIPS and/or the CNSA suite requirements when using cryptography.Of course, if you can get away with Ed25519, use Ed25519 instead.
If you use P-256, make sure you’re using it with SHA-256. Some implementations may default to something weaker (e.g. SHA-1).
If you’re also going to be performing ECDH with P-256, make sure you use compressed points. There used to be a patent; it died in 2018.
If you can afford it, make sure you use deterministic ECDSA (RFC 6979) or hedged signatures (if fault attacks are relevant to your threat model).
Art: LvJ
NIST P-384 (ECDSA, secp384r1)
NIST P-384 has a larger field than the curves we’ve previously examined, which allows P-384 to target the 192-bit security level. That’s the primary reason why anyone would choose P-384.Naturally, elliptic curve security is more complicated than merely security against the Elliptic Curve Discrete Logarithm Problem (ECDLP).
P-384 is most often paired with SHA-384, which is the most widely used flavor of the SHA-2 family hash functions that isn’t susceptible to length-extension attacks. (There are also truncated SHA-512 variants specified later, but that’s also what SHA-384 is under-the-hood.)
If you’re aiming to build a “secure-by-default” tool for a system that the US government might one day become a customer of, with minimal cryptographic primitive choice, using NIST P-384 with SHA-384 makes for a reasonably minimalistic bundle.
Why Not Use P-384?
Unlike P-256, most P-384 implementations don’t use constant-time, optimized, and/or formally verified assembly code. (Notable counter-examples: AWS-LC and Go x/crypto.)Like P-256, P-384 also requires a secure randomness source to sign data. If you aren’t providing one, expect your signing key to end up on fail0verflow one day.
Guidance for P-384
If you use P-384, make sure you’re using it with SHA-384.The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.
Art: Kyume
NIST P-521 (ECDSA, secp521r1)
Biggest curve is best curve! — the cluelesshttps://www.youtube.com/watch?v=i_APoSfCYwU
Systems that choose P-521 often have an interesting threat model, even though said threat model is rarely formally specified.
It’s overwhelmingly likely that what eventually breaks the 256-bit elliptic curves will also break P-521 in short order: Cryptography Relevant Quantum Computers.
The only thing P-521 does against CRQCs that P-256 doesn’t is require more quantum memory. If you’re worried about QRQCs, you might want to look into hybrid post-quantum signature schemes.
If you’re choosing P-521 in your designs, you’re basically saying, “I want to have 256 bits of asymmetric cryptographic security, come hell or high water!” even though the 128-bit security level is likely just fine for your actual threats.
Aside: P-521 and 512-bit ECC Security
P-521 is not a typo, although people sometimes think it is. P-521 uses the Mersenne primeinstead of a 512-bit near-Mersenne prime.
This has led to an unfortunate trend in cryptography media to map ECC key sizes to symmetric security levels that misleads people as to the relationship between the two. For example:
Regrettably, this is misleading, because plotting the ECC Key Size versus equivalent Symmetric Security isn’t a how ECDLP security works. The ratio of the exponents involved is totally linear; it doesn’t suddenly increase beyond 384-bit curves for a mysterious mathematical reason.
- 256-bit Curves target the 128-bit security level
- 384-bit Curves target the 192-bit security level
- 512-bit Curves target the 256-bit security level
- 521-bit Curves actually target the 260-bit security level, but that meets or exceeds the 256-bit security level, so that’s how the standards are interpreted
The reason for this boils down entirely to the best attack against the Elliptic Curve Discrete Logarithm Problem: Pollard’s Rho, which recovers the secret key from an
-bit public key (which has a
search space) in
guesses.
Taking the square root of a number is the same as halving its exponent, so the security level is half:
.
Takeaway: If someone tells you that you need a 521-bit curve to meet the 256-bit security level, they are mistaken and it’s not their fault.
Art: Harubaki
Why Not Use P-521?
It’s slow. Much slower than P-256 and Ed25519. Modestly slower than P-384.Unlike P-384, you’re less likely to find an optimized, constant-time P-521 implementation.
Guidance for P-521
First, make a concerted effort to figure out the motivation for P-521 in your designs. Chances are, someone is putting too much emphasis on the wrong things for security.If you use P-521, make sure you’re using it with SHA-512.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.
Art: LvJ
Ed448 (EdDSA, Curve448)
Ed448 is the P-521 of the Edwards curves: It mostly exists to give standards committees a psychological comfort for the unlikely event that 256-bit ECC is desperately broken but ECC larger than 384 bits is somehow still safe.https://twitter.com/dchest/status/703017144053833728
The very concept of having multiple “security levels” for raw cryptography primitives is mostly an artefact of the historical military roots of cryptography, rather than a serious consideration in the modern world.
Unfortunately, this leads to implementations that prioritize runtime algorithm selection negotiation, which maximizes the risk of protocol-level vulnerabilities. See also: JWT.
Ed448 was specified to use SHAKE256, which is a needlessly conservative decision which leads to an unnecessary performance bottleneck.
Why Not Use Ed448?
Aside from the performance hit mentioned previously, there’s no compelling reason to avoid Ed448 that isn’t also true of either Ed25519 or P-384.Guidance for Ed448
If you want more speed, go with Ed25519. In addition to being faster, Ed25519 is also very widely supported.If you need a prime-order field, use Decaf with Ed448 or consider P-384.
The Brainpool Curves
The main motivation for the Brainpool curves is that the NIST curves were not generated in a “verifiable pseudo-random way”.The only reasons you’d ever want to support the Brainpool curves include:
- You think the NIST curves are somehow backdoored by the NSA
- You don’t appreciate small attack surfaces in cryptography libraries
- The German government told you to (see: compliance)
Most of the advice for the NIST Curves at each security level can be copy/pasted for the Brainpool curves, with one important caveat:
When considering real-world implementations, Brainpool curves are more likely to use the general purpose Big Number procedures (which aren’t always constant-time), rather than optimized assembly code, than the NIST curves are.
Therefore, my general guidance for the Brainpool curves is simply:
- Proceed at your own peril
- Consider hiring a cryptography engineer to study the implementation you’re relying on, especially with regard to timing attacks
Me when I hear “brainpool”
Art: LvJRe-Examining the SafeCurves Criteria
Here’s a 2022 refresh of the SafeCurves criteria for all of the curves considered by this blog post.
SafeCurve Criteria Relevance to the Curves Listed Above Fields All relevant curves satisfy the requirements Equations All relevant curves satisfy the requirements Base Points All relevant curves satisfy the requirements Rho All relevant curves satisfy the requirements Transfers All relevant curves satisfy the requirements Discriminants Only secp256k1 doesn’t satisfy the requirements (out of the curves listed in this blog post) Rigidity The NIST curves do not meet this requirement.
If you care about whether or not the standards were manipulated to insert a backdoor, rigidity matters to you. Otherwise, it’s not a deal-breaker.Ladders While a Montgomery ladder is beneficial for speed and implementation security, it isn’t strictly speaking required.
This is an icing-on-the-cake consideration.Twists The only curve listed above that doesn’t meet the requirement is the 256-bit Brainpool curve (brainpoolp256t1). Completeness All relevant curves satisfy the requirements, as of 2015.
SafeCurves is out of date here.Indistinguishability All relevant curves satisfy the requirements, as of 2014. SafeCurves continues to be a useful resource, especially if you stray from the guidance on this page.
For example: You wouldn’t want to use pairing-friendly curves for general purpose ECC digital signatures, because they’re suitable for specialized problems. SafeCurves correctly recommends not using BN(2,254).
However, SafeCurves is showing its age in 2022. BN curves still end up in digital signature protocol standards even though BLS-12-381 is clearly a better choice.
The Internet would benefit greatly for an updated SafeCurves that focuses on newer elliptic curve algorithms.
Art: Scruff
TL;DR
Ed25519 is great. NIST P-256 and P-384 are okay (with caveats). Anything else is questionable, and their parameter selection should come with a clear justification.https://soatok.blog/2022/05/19/guidance-for-choosing-an-elliptic-curve-signature-algorithm-in-2022/
#asymmetricCryptography #BrainpoolCurves #cryptography #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #ellipticCurveCryptography #P256 #P384 #P521 #secp256k1 #secp256r1 #secp384r1 #secp521r1 #SecurityGuidance

Programmers don’t understand hash functions, and I can demonstrate this to most of the people that will read this with a single observation:
When you saw the words “hash function” in the title, you might have assumed this was going to be a blog post about password storage. (Passwords are the most common knee-jerk reaction I get to any discussion about hash functions, anyway. A little bit of security knowledge can be very dangerous.)
I don’t blame software developers for their lack of understanding on anything I’m going to discuss. The term “hash function” can accurately represent any of the following disparate topics in computer science:
- Converting keys into memory addresses for hash maps
- Creating a one-way message digest to ensure said was transmitted correctly over an untrusted network
- Cryptographic building blocks for digital signatures, message authentication codes, key derivation functions, and so on
- Server-side password storage techniques meant to resist brute force and precomputation attacks
- Perceptual fingerprints of visual data
Some hash functions are reusable across multiple topics from the above list, but even then, not all of the hash functions you’d use for one purpose have the same properties.
Using a hash function for the wrong purpose, or in a place where it doesn’t provide the expected properties, can lead to security vulnerabilities. Some of these vulnerabilities aren’t obvious or straightforward, either, which only serves to magnify confusion.
So let’s talk about hash functions, what programmers get wrong about them, and the correct answers to these common misconceptions.

What Are Hash Functions?
A hash function is any function that can map an arbitrary-sized input to a fixed-size output.
This is incredibly vague; anything can be a hash function if you’re brave enough. You can treat an arbitrary string as an big integer and return the least significant bit and call this a hash function. (It’s not a particularly good one, but it fits the definition.)
function totallyHashed(input: string|Buffer): Buffer { const inBuf = Buffer.isBuffer(input) ? input : Buffer.from(input); return Buffer.from([ inBuf[inBuf.length - 1] & 1 ]);}
Being able to call something a hash function and be technically correct isn’t very helpful.

What Kinds of Hash Functions Do We Care About?
There are different types of hash functions suitable for solving different types of problems. (Some examples follow, but this should not be taken as an exhaustive treatment.)
General-Purpose Hash Functions
General-purpose hash functions are useful for converting a key into an index for memory addresses when constructing hash tables. Usually when someone says only “hash function” in a broad computer science context, without any qualifiers, that’s what they’re talking about.
Examples: SipHash, djb2, Murmur3. You can find a comparison here.
Worth calling out: Only some of these general purpose tables are safe to use for hash tables where the keys are provided from user input. For example: JSON data. When in doubt, SipHash-2-4 is a good default.
Cryptographic Hash Functions
Cryptographic hash functions have additional desirable properties (they’re non-invertible and must be resistant to collision attacks and preimage attacks) above general-purpose hash functions. They also have larger output sizes (typically at least 256 bits) than the sort of hash functions you’d use for hash tables. Consequently, they’re slower than the hash functions people tend to use for hash tables.
Cryptographic hash functions are often used in place of a random oracle in security protocols, because actual random oracles do not exist, as Thomas Pornin explains:
A random oracle is described by the following model:
- There is a black box. In the box lives a gnome, with a big book and some dice.
- We can input some data into the box (an arbitrary sequence of bits).
- Given some input that he did not see beforehand, the gnome uses his dice to generate a new output, uniformly and randomly, in some conventional space (the space of oracle outputs). The gnome also writes down the input and the newly generated output in his book.
- If given an already seen input, the gnome uses his book to recover the output he returned the last time, and returns it again.
So a random oracle is like a kind of hash function, such that we know nothing about the output we could get for a given input message m. This is a useful tool for security proofs because they allow to express the attack effort in terms of number of invocations to the oracle.
The problem with random oracles is that it turns out to be very difficult to build a really “random” oracle. First, there is no proof that a random oracle can really exist without using a gnome. Then, we can look at what we have as candidates: hash functions. A secure hash function is meant to be resilient to collisions, preimages and second preimages. These properties do not imply that the function is a random oracle.
Thomas Pornin
I’m intentionally eschewing a lot of detail about what makes a cryptographic hash function secure (e.g. bit diffusion even in reduced rounds), or how they achieve the desirable properties.
If you’re interested in those topics, leave a comment below and I’ll talk about that in a future post.
If you remember nothing else about cryptographic hash functions, just know that checksums (e.g. CRC32) are not cryptographic. (Yes, many hashing APIs include CRC32 alongside good options, but don’t be misled.)
Note: There’s a very pedantic mathematical discussion that can be had about whether or not cryptographic hash functions are truly one-way functions (which, like P = NP vs P != NP, is an open conjecture in mathematics). You don’t have to know, or even care, about this distinction–unless you’re making assumptions about this property in your designs.
Examples: BLAKE3, SHA256.

A Word Of Caution on Message Authentication Codes
In cryptography, message authentication codes are often built with cryptographic hash functions, but not always!
AES-GCM famously uses a function called GHASH, which evaluates a polynomial in 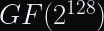
Poly1305 is a similar story to GCM, but doesn’t reuse keys the same way.
Although GHASH and Poly1305 are secure MACs, they’re not built from cryptographic hash functions.
CBC-MAC uses a block cipher (typically AES) in cipher-block chaining mode (with an all-zero initialization vector) and outputs the last block as the authentication tag. This offers no collision resistance (as Mega learned the hard way).
When in doubt, HMAC is a safe choice.
Password Hashing Functions
Separate from, but often built from, cryptographic hash functions are password hashing functions. These are the tools you use if your users are sending a username and password over HTTP and you don’t want to become the next RockYou.
Examples: Argon2, scrypt, bcrypt.
Password hashing functions have significant overlap with key-derivation functions (KDFs), but not all KDFs are meant for password hashing, and not all password hashes are meant for key derivation.
It’s perfectly reasonable to use bcrypt to store passwords, but not to derive encryption keys.
Conversely, HKDF is a valid KDF (which has a stricter set of security requirements than a PRF), but it’s not meant for passwords.
Some algorithms (Argon2 and scrypt) can be safely used as a password hashing function or as a KDF.
Modern password hashing algorithms involve a deliberately expensive computation that’s fast to verify once, but expensive to verify multiple times. These algorithms can be tuned (memory usage, parallel threads, number of iterations) to target a specific latency goal. Additionally, most password hashing APIs take care of salt generation for you, using a secure random generator.
Perceptual Hashes
In yet another different direction, you have perceptual hash functions, such as the kind Apple is going to use to violate the privacy of their customers in a desperate attempt to catch a small percentage of depraved individuals peddling CSAM (and expecting the rest of their customers to blindly trust that this capability they built for themselves will never ever be used to stifle dissidents or whistleblowers).
https://twitter.com/matthew_d_green/status/1428414174758117389
I don’t have a lot to say here, except that I don’t trust Apple, especially after the internal memo about “screeching voices of the minority”: Their partners on this project have showed the utmost contempt for privacy activists, LGBTQ+ folks, survivors of child sexual abuse, etc. and they remain committed to them. Fuck Apple.
Suffice to say, cryptographers were not at all surprised by the discovery of practical collisions against Apple’s new perceptual hash function, because perceptual hash functions do not provide the same properties as cryptographic hash functions.
Perceptual hashes of CSAM do not provide collision or preimage resistance, and it would be possible to flood Apple with false positives if a hash of such material were to ever leak publicly. (Maybe an enterprising Internet Troll will one day make a meme generator that does this?)
How Developers Misuse Hash Functions
There are far too many ways that hash functions get misused by software developers to recount in one blog post.
Some of the more common and obvious examples (i.e., using MD5 to store passwords, calling SHA256 “encryption”) aren’t very interesting, and are covered elsewhere, so I’m going to focus on misuse examples that aren’t commonly discussed online.
Encrypt and Hash
A common design pattern from the 2010’s is to hash some data, then encrypt the data that was hashed (but not the hash), and then send both values to another machine.
The expectation here is that, upon decrypting the ciphertext, the hash can be used as a client-side fingerprint to ensure the data wasn’t corrupted in storage.
This use of a hash function is distinct from the Encrypt/MAC discussion (see: the Cryptographic Doom Principle), because it’s often implemented alongside AEAD. (If you aren’t using authenticated encryption, correct that first.)
However, there are two problems here:
- Directly invoking cryptographic hash functions doesn’t involve a cryptographic secret, and thus all clients will produce the same hash of the same plaintext.
- A cryptographic hash can be used to perform offline attacks (e.g. rainbow tables) against the plaintext, especially if the input domain is small (i.e. a phone number).

What you really want to use in this situation is HMAC with a static secret key (which is only known client-side).
HMAC ensures that, without access to the secret key, precomputation attacks are not possible. Additionally, if each client has a different secret key (which, they SHOULD), an attacker who only has access to hashes and ciphertext cannot distinguish which records correspond across multiple clients.
This is a weaker proposition than security against chosen plaintexts (IND-CPA), but still provides a higher level of assurance than a naked SHA256 hash.
Searchable Encryption with Hashed Indexes
Similar to the previous example, sometimes developers will be tasked with storing encrypted values in a database while also being able to quickly query the database based on an encrypted value.
The laziest solution to the “encrypted database” use-case is to just use deterministic encryption, such as AES-ECB or with a static IV/nonce. Most people who have some familiarity with cryptography immediately recognize that this is dangerous, so they opt to encrypt securely (i.e. AEAD with random nonces).
However, to support querying, they often just hash their plaintext and store it alongside the ciphertext.

This reintroduces the issues from the previous section (especially rainbow tables), but with additional risks:
- Plaintexts are overwhelmingly likely to have smaller input domains, thereby increasing the utility of hashes to attack the confidentiality of the plaintext.
- No domain separation between different hashes of different encrypted fields.
To address this, there are a few things you can do:
- Truncate your hashes. If you want to frustrate attackers, simply don’t store a full hash of the plaintext. Instead, truncate hashes to 8 or fewer hexits and permit a small degree of false positives in your decryption logic (n.b. by filtering those rows out).
- Use distinct HMAC keys per index. This introduces the solution to the previous section, but also addresses domain separation.
If you’re left wondering, “Can I use both solutions?” The answer is, “Yes, but you just reinvented what CipherSweet calls blind indexes.”

Overconfidence With Collision-Resistance
Previously on this blog, I disclosed a trivial collision vulnerability in the Kerl hash function used by the Iota cryptocurrency project without breaking the underling hash function (Keccak384).
How did I do this? I found multiple input values that, before being passed to the hash function, collide with each other.

Developers are frequently overconfident about the collision-resistance of their protocol, simply because they use collision-resistant hash functions inside of the protocol. They’re frequently blind to the reality of canonicalization attacks (including the somewhat famous length-extension attack).
This isn’t their fault. If you’ve made this mistake, it isn’t your fault. Cryptography is a difficult topic and requires a lot of experience and expertise to get right.
Closing Thoughts
One of my favorite cryptography websites is for the SPHINCS project, which is a stateless post-quantum hash-based digital signature algorithm.
On this webpage, which has a heavy anarchist aesthetic, there’s a special note to law-enforcement agents that reads:
The word “state” is a technical term in cryptography. Typical hash-based signature schemes need to record information, called “state”, after every signature. Google’s Adam Langley refers to this as a “huge foot-cannon” from a security perspective. By saying “eliminate the state” we are advocating a security improvement, namely adopting signature schemes that do not need to record information after every signature. We are not talking about eliminating other types of states. We love most states, especially yours! Also, “hash” is another technical term and has nothing to do with cannabis.
Now, I personally like this disclaimer because a) it’s funny and b) it reminds us that all cops are bastards.

But it’s also a good reminder of how confusing the term “hash” can be in different fields. Software engineers aren’t the only people who are likely to be confused about hash functions.
(And I can’t even apply the “-ish” suffix to talk about things that behave like hash functions but aren’t hash functions, because that’s a homograph for an even more specific drug term.)
The next time you see a programmer ask a potentially unwise question involving hash functions, having read this blog post, I hope you’ll appreciate how confusing all this shit can be for virtually everyone.
If you’ve made any of the specific mistakes I’ve discussed here, know that you’re in very good company. Some of the best programmers in the industry have made these mistakes before. Hell, I’ve made these exact mistakes before, and worse.
https://soatok.blog/2021/08/24/programmers-dont-understand-hash-functions/
#cryptographicHashFunction #cryptography #hashFunction #SecurityGuidance
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Art by Khia.
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting
(at 50% probability) blocks.
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
you expect from AES.
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.This is because Grover’s quantum search algorithm can search
unsorted items in
time, which can be used to reduce the total number of possible secrets from
to
. This effectively cuts the security level, expressed in bits, in half.
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
(plaintext, key) pairs that produce any given ciphertext block.
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
times as many AES-256 keys as there are possible plaintext/ciphertexts. Keep this in mind for AES-GCM.
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
This is unacceptable!
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
: A number that must only be used once).
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
The deeper you look into AES-GCM’s design, the harder you will feel this sticker.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called. This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
This is often sold as an advantage: Reusingallows for better performance. However, it makes GCM brittle: Reusing a nonce allows an attacker to recover H and then forge messages forever. This is called the “forbidden attack”, and led to real world practical breaks.
Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.If we assume AES is well-behaved, we can deduce that there are approximately
different 256-bit keys that will map a single plaintext block to a single ciphertext block.
This is trivial to calculate. Simply divide the number of possible keys (
) by the number of possible block states (
) to yield the number of keys that produce a given ciphertext for a single block of plaintext:
.
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
.
This means there are approximately
independent keys that will map a given all-zero plaintext block to an arbitrarily chosen value of
(if we assume AES doesn’t have weird biases).
Credit: Harubaki
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection ofas a 128-bit pseudorandom function, rather than a 128-bit permutation. As a result, you an expect a collision with 50% probability after only
different keys are selected.
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a
collision risk. So that means our safety limit is actually
different AES keys before you have to worry about
reuse.
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of
different AES keys, you have to either accept the risk or stop using AES-GCM.
If you have a billion users (
), the safety limit is breached after
AES keys per user (approximately 262,000).
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.is used for block multiplication, and
(the value of
with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.
The arrow highlighted with green is HF.
It’s tempting to think that a reuse of
isn’t a concern because
will necessarily be randomized, which prevents an attacker from observing when
collides. It’s certainly true that the single-block collision risk discussed previously for
will almost certainly not also result in a collision for
. And since
isn’t reused unless a nonce is reused (which also leaks
directly), this might seem like a non-issue.
Art by Khia.
However, it’s straightforward to go from a condition of
reuse to an adaptive chosen-ciphertext attack.
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- Use your knowledge of
, the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of
for a given nonce.
- Calculate a new authentication tag for a chosen ciphertext using
and your candidate
value, then replay it into the target system.
While the blinding offered by XORing the final output with
is sufficient to stop
from being leaked directly, the protection is one-way.
Ergo, a collision in
is not sufficiently thwarted by
.
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
is
, and finding an untargeted collision requires being able to observe more than
different sessions, and somehow distinguish when
collides.
As a user, you know that after
different keys, you’ve crossed the safety boundary for avoiding
collisions. But as an attacker, you need
bites at the apple, not
. Additionally, you need some sort of oracle or distinguisher for when this happens.
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
is challenging to work with. You would need the computational and data storages of a major cloud service provider to even think about pulling the attack off.
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
bytes long, under a given (key, nonce) pair.
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
messages.
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atrandom nonces, which represents a collision probability of one in 4 billion.
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
I’m glad you asked!
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
messages (for the same collision probability as AES-GCM).
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography

Canonicalization Attacks occur when a protocol that feeds data into a hash function used in a Message Authentication Code (MAC) or Digital Signature calculation fails to ensure some property that’s expected of the overall protocol.
The textbook example of a canonicalization attack is the length-extension attack against hash functions such as MD5–which famously broke the security of Flickr’s API signatures.
But there’s a more interesting attack to think about, which affects the design of security token/envelope formats (PASETO, DSSE, etc.) and comes up often when folks try to extend basic notions of authenticated encryption (AE) to include additional authenticated (but unencrypted) data (thus yielding an AEAD mode).
Let’s start with a basic AE definition, then extend it to AEAD poorly, then break our extension. Afterwards, we can think about strategies for doing it better.
Turning CTR+HMAC into AEAD
Signal uses AES-CBC then HMAC-SHA2 to encrypt messages between mobile devices.
We often refer to this shape as “CBC+HMAC” (although this is a few typos away from being confused with a very different idea called CBC-MAC).
When CBC+HMAC is used with the AES block cipher with 256-bit keys and HMAC-SHA2, it becomes AES-256-CBC+HMAC-SHA256. What a mouthful!

(Art by Lynx vs Jackalope)
In modern designs, AES-CTR is often preferable to AES-CBC, since you don’t have to deal with padding (or padding oracles).
Most systems these days prefer GCM over CBC+HMAC or CTR+HMAC. I don’t like AES-GCM (especially if your use-case is “support platforms without hardware acceleration”), but it’s hardly the worst choice for most applications. AES-GCM is a dedicated AEAD mode, while CBC+HMAC and CTR+HMAC merely provide AE.
Why Does Additional Data Matter?

The main purpose of Additional Data (the AD in AEAD) is to bind an encrypted payload (ciphertext + authentication tag) to a given context. This is extremely helpful in mitigating Confused Deputy attacks.
Critically, this additional data is not encrypted. (At least, on this level; it’s probably wise to communicate over HTTPS!)
Naive CTR+HMAC to AEAD Extension
In a normal CTR+HMAC definition, your algorithm looks something like this:
- Generate a random nonce equal to the block size of your block cipher. (16 bytes for AES.)
- Encrypt your message with AES-CTR, using the given key and IV.
- Calculate the HMAC-SHA2 output of the IV followed by the ciphertext from step 2.
- Return IV, Ciphertext, MAC.
Decryption basically runs steps 3 and 2 in reverse: Recalculate the MAC (in constant-time!), decrypt ciphertext, return plaintext.
The most obvious way to extend this design to support additional authenticated data is to append it to the ciphertext.
This yields the following updated protocol:
- Generate a random nonce equal to the block size of your block cipher. (16 bytes for AES.)
- Encrypt your message with AES-CTR, using the given key and nonce.
- Calculate the HMAC-SHA2 output of the IV followed by the ciphertext from step 2, then the additional authenticated data.
- Return IV, Ciphertext, MAC.
Suffice to say, this is not a secure construction.
The Canonicalization Attack
Let’s say you built this extended protocol to encrypt a payload that looks like a URI string, but wanted to bind the token to a given browser session, so you use the HTTP User-Agent header as the AAD.
When you generate a token, you might produce the following:
const crypto = require('crypto');function splitKey(key) { let hmac; hmac = crypto.createHmac('sha256', key); hmac.update('encrypt-key'); let Ek = hmac.digest(); hmac = crypto.createHmac('sha256', key); hmac.update('hmac-key'); let Ak = hmac.digest(); return [Ek, Ak];}function encryptWithContext(plaintext, aad, key) { let [encKey, authKey] = splitKey(key); console.log(encKey, authKey); let nonce = crypto.randomBytes(16); const aes = crypto.createCipheriv('aes-256-ctr', encKey, nonce); const ciphertext = aes.update(plaintext); aes.final(); // Pay attention to this part: const hmac = crypto.createHmac('sha256', authKey); hmac.update(nonce); hmac.update(ciphertext); hmac.update(aad); return [nonce, ciphertext, hmac.digest()];}let plaintext = [ 'expires=1630223780', 'access_group=1234', 'subject=auth-v2.example.com', 'restrictions=on'].join('&');// expires=1630223780&access_group=1234&subject=auth-v2.example.com&restrictions=on// const key = crypto.randomBytes(32);let [nonce, ciphertext, tag] = encryptWithContext(plaintext, userAgent, key);
So here’s the clever attack: If you can shift bytes from the payload into the prefix of your User-Agent string, they’ll produce the same HMAC tag.
Attackers can truncate as much of the payload as they want by prepending it to the User-Agent included in their HTTP request.
You can even turn this:
expires=1630223780&access_group=1234&subject=auth-v2.example.com&restrictions=on
…into this:
expires=1630223780&access_group=1234&subject=auth-v2.example.com
…without invalidating the existing authentication tag–just by ensuring that the last 16 bytes of ciphertext are prepended to your User-Agent and removed from the payload.
More broadly, any time you have a multi-part message being fed into a hash function, if you aren’t careful with how you feed it into the hash function, you can induce trivial collisions.
See also: Iota’s Kerl hash function.
This is obviously true, because hash functions are deterministic: The same input will always produce the same output. If you can control one or more parts of a multi-part message, you can collide the input–thereby creating a collision in the output.
This can affect any protocol that depends on hash functions, but most obviously, HMAC and Digital Signature algorithms are in scope.
But what does “being careful” look like? Let’s look at a safe example.
Pre-Authentication Encoding (PAE)
Earlier I had mentioned PASETO and DSSE. They both have this notion of a “PAE” algorithm which aims to prevent canonicalization attacks.
PASETO’s definiton for PAE is as follows:
function LE64(n) { var str = ''; for (var i = 0; i < 8; ++i) { if (i === 7) { // Clear the MSB for interoperability n &= 127; } str += String.fromCharCode(n & 255); n = n >>> 8; } return str;}function PAE(pieces) { if (!Array.isArray(pieces)) { throw TypeError('Expected an array.'); } var count = pieces.length; var output = LE64(count); for (var i = 0; i < count; i++) { output += LE64(pieces.length); /*** Soatok Note: This JS pseudocode incorrectly assumes strings, rather than buffers. It's only meant to illustrate the idea. In real implementations, don't join Buffers with +. ***/ output += pieces[i]; } return output;}
What this does (with all lengths as 64-bit unsigned integers, serialized as 8 bytes):
- Prepend the number of parts being hashed.
- For each part, first prefix its length, then its value.
This is an obvious mitigation for canonicalization attacks:
- If you feed in a different number of pieces, the count (the first 8 bytes) will differ.
- If you try to move data from one piece to another, you’ll produce different lengths for both pieces, which will not yield an input collision to the hash function.
However, it’s important that both mechanism are in play to guarantee security:
- Without the length prefixes, we’re no different than the CTR+HMAC extension we defined above.
- Without the count prefix, it’s possible to drop pieces and then include a dummy “length” in the payload of others to create an input collision.
What’s an Input Collision?
First, you need to know what a collision attack is.
Consider a hash function, H(). If you can identify any two input messages (m1, m2) such that H(m1) = H(m2), you’ve found a collision in the output of the hash function.
An input collision is dumber than that.
If m1 is constructed from multiple segments with different meanings, you don’t need an m2. Just find multiple ways (the collisions) to result in the same m1 value (the input).
That’s what we did earlier when we shifted bytes from the ciphertext to the user agent.
DSSE Leaves Me Dizzy
It should come as no surprise that I find DSSE’s definition of PAE to be somewhat bizarre.
PAE(type, body) = "DSSEv1" + SP + LEN(type) + SP + type + SP + LEN(body) + SP + body+ = concatenationSP = ASCII space [0x20]"DSSEv1" = ASCII [0x44, 0x53, 0x53, 0x45, 0x76, 0x31]LEN(s) = ASCII decimal encoding of the byte length of s, with no leading zeros
The only thing that saves them from canonicalization attacks is that the number of pieces is constant.
If the number of pieces was variable (e.g. if the KEYID was optionally included in the signature, but they forgot to always include a hard-coded 0 length if it was absent), you could defeat their flavor of PAE by constructing two different messages that produce the same hash in the digital signature algorithm.
This is because the number of pieces isn’t included in the DSSE definition. (If they ever support a variable number of components, and fail to include the count in the signature, they’ll be vulnerable.)
Amusingly, the rationale page for DSSE using PAE states:
- Why use PAE?
- Because we need an unambiguous way of serializing two fields, payloadType and payload. PAE is already documented and good enough. No need to reinvent the wheel.
…Yet, they didn’t actually [i]use the “already documented and good enough” definition of PAE from PASETO.

(Art by Lynx vs Jackalope)
Fixing AES-CTR+HMAC with PAE
This is pretty straightforward patch:
function encryptWithContext(plaintext, aad, key) { let [encKey, authKey] = splitKey(key); console.log(encKey, authKey); let nonce = crypto.randomBytes(16); const aes = crypto.createCipheriv('aes-256-ctr', encKey, nonce); const ciphertext = aes.update(plaintext); aes.final(); // Pay attention to this part: const hmac = crypto.createHmac('sha256', authKey);- hmac.update(nonce);- hmac.update(ciphertext);- hmac.update(aad);+ hmac.update(PAE([nonce, ciphertext, aad])); return [nonce, ciphertext, hmac.digest()]; }
The only conceivable way to attack this design is to aim for an integer overflow, which will require sending at least 2^63 bytes–at which point, you’re more likely to DDoS the target than succeed.
Wrapping Up
Canonicalization Attacks broadly aren’t well-understood or widely appreciated risks with cryptography protocol design outside of specialist circles (although many application security folks are at least aware of specific instances, i.e. Length Extension).
Part of the reason for this lack of knowledge transfer is that all of the AEAD modes defend against it by design, and most artisanal authenticated encryption constructions don’t bother with additional authenticated data, and most home-made cryptography protocols don’t even authenticate their ciphertexts correctly, and …
You get the point, I hope. There’s unaddressed concerns all the way down. Expecting people who aren’t specialized experts in this specific field to get all of them right is frankly unreasonable. In practice, outside of cryptography, canonicalization either doesn’t matter or there’s something else wrong that’s far more urgent.
https://soatok.blog/2021/07/30/canonicalization-attacks-against-macs-and-signatures/
#collisionAttacks #cryptographicHashFunction #cryptography #digitalSignatureAlgorithm #DSSE #HMAC #lengthExtensionAttacks #MACs #PASETO #SecurityGuidance
This is the first entry in a (potentially infinite) series of dead end roads in the field of cryptanalysis.Cryptography engineering is one of many specialties within the wider field of security engineering. Security engineering is a discipline that chiefly concerns itself with studying how systems fail in order to build better systems–ones that are resilient to malicious acts or even natural disasters. It sounds much simpler than it is.
If you want to develop and securely implement a cryptography feature in the application you’re developing, it isn’t enough to learn how to implement textbook descriptions of cryptography primitives during your C.S. undergrad studies (or equivalent). An active interest in studying how cryptosystems fail is the prerequisite for being a cryptography engineer.
Thus, cryptography engineering and cryptanalysis research go hand-in-hand.
Pictured: How I feel when someone tells me about a novel cryptanalysis technique relevant to the algorithm or protocol I’m implementing. (Art by Khia.)
If you are interested in exploring the field of cryptanalysis–be it to contribute on the attack side of cryptography or to learn better defense mechanisms–you will undoubtedly encounter roads that seem enticing and not well-tread, and it might not be immediately obvious why the road is a dead end. Furthermore, beyond a few comparison tables on Wikipedia or obscure Stack Exchange questions, the cryptology literature is often sparse on details about why these avenues lead nowhere.
So let’s explore where some of these dead-end roads lead, and why they stop where they do.
(Art by Kyume.)
Length Extension Attacks
It’s difficult to provide a better summary of length extension attacks than what Skull Security wrote in 2012. However, that only addresses “What are they?”, “How do you use them?”, and “Which algorithms and constructions are vulnerable?”, but leaves out a more interesting question: “Why were they even possible to begin with?”An Extensive Tale
Tale, not tail! (Art by Swizz.)
To really understand length extension attacks, you have to understand how cryptographic hash functions used to be designed. This might sound intimidating, but we don’t need to delve too deep into the internals.
A cryptographic hash function is a keyless pseudorandom transformation from a variable length input to a fixed-length output. Hash functions are typically used as building blocks for larger constructions (both reasonable ones like HMAC-SHA-256, and unreasonable ones like my hash-crypt project).
However, hash functions like SHA-256 are designed to operate on sequential blocks of input. This is because sometimes you need to stream data into a hash function rather than load it all into memory at once. (This is why you can sha256sum a file larger than your available RAM without crashing your computer or causing performance headaches.)
A streaming hash function API might look like this:
class MyCoolHash(BaseHashClass): @staticmethod def init(): """ Initialize the hash state. """ def update(data): """ Update the hash state with additional data. """ def digest(): """ Finalize the hash function. """ def compress(): """ (Private method.) """
To use it, you’d callhash = MyCoolHash.init()and then chain togetherhash.update()calls with data as you load it from disk or the network, until you’ve run out of data. Then you’d calldigest()and obtain the hash of the entire message.There are two things to take away right now:
- You can call
update()multiple times, and that’s valid.- Your data might not be an even multiple of the internal block size of the hash function. (More often than not, it won’t be!)
So what happens when you call
digest()and the amount of data you’ve passed toupdate()is not an even multiple of the hash size?For most hash functions, the answer is simple: Append some ISO/IEC 7816-4 padding until you get a full block, run that through a final iteration of the internal compression function–the same one that gets called on
update()–and then output the current internal state.Let’s take a slightly deeper look at what a typical runtime would look like for the MyCoolHash class I sketched above:
hash = MyCoolHash.init()
- Initialize some variables to some constants (initialization vectors).
hash.update(blockOfData)
- Start with any buffered data (currently none), count up to 32 bytes. If you’ve reached this amount, invoke
compress()on that data and clear the buffer. Otherwise, just append blockOfData to the currently buffered data.- For every 32 byte of data not yet touched by
compress(), invokecompress()on this block (updating the internal state).- If you have any leftover bytes, append to the internal buffer for the next invocation to process.
hash.update(moreData)
- Same as before, except there might be some buffered data from step 2.
output = hash.digest()
- If you have any data left in the buffer, append a 0x80 byte followed by a bunch of 0x00 bytes of padding until you reach the block size. If you don’t, you have an entire block of padding (0x80 followed by 0x00s).
- Call
compress()one last time.- Serialize the internal hash state as a byte array or hexadecimal-encoded string (depending on usage). Return that to the caller.
This is fairly general description that will hold for most older hash functions. Some details might be slightly wrong (subtly different padding scheme, whether or not to include a block of empty padding on
digest()invocations, etc.).The details aren’t super important. Just the rhythm of the design.
init()update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
- …
digest()
- load buffer, pad,
compress()- serialize internal state
- return
And thus, without having to know any of the details about what
compress()even looks like, the reason why length extension attacks were ever possible should leap out at you!
Art by Khia.
If it doesn’t, look closely at the difference between
update()anddigest().There are only two differences:
update()doesn’t pad before callingcompress()digest()returns the internal state thatcompress()always mutatesThe reason length-extension attacks are possible is that, for some hash functions, the output of
digest()is its full internal state.This means that you can run take an existing hash function and pretend it’s the internal state after an
update()call instead of adigest()call by appending the padding and then, after callingcompress(), appending additional data of your choice.The (F)Utility of Length Extension
Length-Extension Attacks are mostly used for attacking naive message authentication systems where someone attempts to authenticate a message (M) with a secret key (k), but they construct it like so:
auth_code = vulnerable_hash(k.append(M))
If this sounds like a very narrow use-case, that’s because it is. However, it still broke Flickr’s API once, and it’s a popular challenge for CTF competitions around the world.Consequently, length-extension attacks are sometimes thought to be vulnerabilities of the construction rather than a vulnerability of the hash function. For a Message Authentication Code construction, these are classified under canonicalization attacks.
After all, even though SHA-256 is vulnerable to length-extension, but you can’t actually exploit it unless someone is using it in a vulnerable fashion.
That being said, it’s often common to say that hash functions like SHA-256 and SHA-512 are prone to length-extension.
Ways to Avoid Length-Extension Attacks
Use HMAC. HMAC was designed to prevent these kinds of attacks.Alternatively, if you don’t have any cryptographic secrets, you can always do what bitcoin did: Hash your hash again.
return sha256(sha256(message))
Note: Don’t actually do that, it’s dangerous for other reasons. You also don’t want to take this to an extreme. If you iterate your hash too many times, you’ll reinvent PBKDF1 and its insecurity. Two is plenty.Or you can do something really trivial (which ultimately became another standard option in the SHA-2 family of hash functions):
Always start with a 512-bit hash and then truncate your output so the attacker never recovers the entire internal state of your hash in order to extend it.
That’s why you’ll sometimes see SHA-512/224 and SHA-512/256 in a list of recommendations. This isn’t saying “use one or the other”, that’s the (rather confusing) notation for a standardized SHA-512 truncation.
Note: This is actually what SHA-384 has done all along, and that’s one of the reasons why you see SHA-384 used more than SHA-512.
If you want to be extra fancy, you can also just use a different hash function that isn’t vulnerable to length extension, such as SHA-3 or BLAKE2.
Questions and Answers
Art by Khia.
Why isn’t BLAKE2 vulnerable to length extension attacks?
Quite simply: It sets a flag in the internal hash state before compressing the final buffer.If you try to deserialize this state then invoke
update(), you’ll get a different result than BLAKE2’scompress()produced duringdigest().For a secure hash function, a single bit of difference in the internal state should result in a wildly different output. (This is called the avalanche effect.)
Why isn’t SHA-3 vulnerable to length extension attacks?
SHA-3 is a sponge construction whose internal state is much larger than the hash function output. This prevents an attacker from recovering the hash function’s internal state from a message digest (similar to the truncated hash function discussed above).Why don’t length-extension attacks break digital signature algorithms?
Digital signature algorithms–such as RSASSA, ECDSA, and EdDSA–take a cryptographic hash of a message and then perform some asymmetric cryptographic transformation of the hash with the secret key to produce a signature that can be verified with a public key. (The exact details are particular to the signature algorithm in question.)Length-extension attacks only allow you to take a valid H(k || m) and produce a valid H(k || m || padding || extra) hash that will validate, even if you don’t know k. They don’t magically create collisions out of thin air.
Even if you use a weak hash function like SHA-1, knowing M and H(M) is not sufficient to calculate a valid signature. (You need to be able to know these values in order to verify the signature anyway.)
The security of digital signature algorithms depends entirely on the secrecy of the signing key and the security of the asymmetric cryptographic transformation used to generate a signature. (And its resilience to side-channel attacks.)
However, a more interesting class of attack is possible for systems that expect digital signatures to have similar properties as cryptographic hash functions. This would qualify as a protocol vulnerability, not a length-extension vulnerability.
TL;DR
Art by Khia.
Length-extension attacks exploit a neat property of a few cryptographic hash functions–most of which you shouldn’t be using in 2020 anyway (SHA-2 is still fine)–but can only be exploited by a narrow set of circumstances.
If you find yourself trying to use length-extension to break anything else, you’ve probably run into a cryptographic dead end and need to backtrack onto more interesting avenues of exploitation–of which there are assuredly many (unless your cryptography is boring).
Next: Timing Side-Channels
https://soatok.blog/2020/10/06/dead-ends-in-cryptanalysis-1-length-extension-attacks/
#cryptanalysis #crypto #cryptographicHashFunction #cryptography #lengthExtensionAttacks

Let me state up front that, while we’re going to be talking about an open source project that was recently submitted to Hacker News’s “Show HN” section, the intent of this post is not at all to shame the developer who tried their damnedest to do the right thing. They’re the victim, not the culprit.
RSA, Ya Don’t Say
Earlier this week, an HN user shared their open source fork of a Facebook’s messenger client, with added encryption. Their motivation was, as stated in the readme:
It is known that Facebook scans your messages. If you need to keep using Facebook messenger but care about privacy, Zuccnet might help.It’s pretty simple: you and your friend have Zuccnet installed. Your friend gives you their Zuccnet public key. Then, when you send a message to your friend on Zuccnet, your message is encrypted on your machine before it is sent across Facebook to your friend. Then, your friend’s Zuccnet decrypts the message. Facebook never sees the content of your message.
I’m not a security person and there’s probably some stuff I’ve missed – any contributions are very welcome! This is very beta, don’t take it too seriously.
From Zuccnet’s very humble README.
So far, so good. Facebook is abysmal for privacy, so trying to take matters into your own hands to encrypt data so Facebook can’t see what you’re talking about is, in spirit, a wonderful idea.

However, there is a problem with the execution of this idea. And this isn’t a problem unique to Zuccnet. Several times per year, I come across some well-meaning software project that makes the same mistake: Encrypting messages with RSA directly is bad.
From the Zuccnet source code:
const encryptMessage = (message, recipientPublicKey) => { const encryptedMessage = crypto.publicEncrypt( { key: recipientPublicKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(message), ); return encryptedMessage.toString("base64");};/** * * @param {String} encryptedMessage - base64 encoded string */const decryptMessage = encryptedMessage => { const encryptedMessageBuffer = Buffer.from(encryptedMessage, "base64"); const { privateKey } = getOrCreateZuccnetKeyPair(); const message = crypto.privateDecrypt( { key: privateKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(encryptedMessageBuffer), );};
To the Zuccnet author’s credit, they’re using OAEP padding, not PKCS#1 v1.5 padding. This means their code isn’t vulnerable to Bleichenbacher’s 1998 padding oracle attack (n.b. most of the RSA code I encounter in the wild is vulnerable to this attack).
However, there are other problems with this code:
- If you try to encrypt a message longer than 256 bytes with a 2048-bit RSA public key, it will fail. (Bytes matter here, not characters, even for English speakers–because emoji.)
- This design (encrypting with a static RSA public key per recipient) completely lacks forward secrecy. This is the same reason that PGP encryption sucks (or, at least, one of the reasons PGP sucks).
There are many ways to work around the first limitation.
Some cryptography libraries let you treat RSA as a block cipher in ECB mode and encrypt each chunk independently. This is an incredibly stupid API deign choice: It’s slow (asymmetric cryptography operations are on the order of tens-to-hundreds-of-thousands times slower than symmetric cryptography) and you can drop/reorder/replay blocks, since ECB mode provides no semantic security.

(Art by Swizz.)
A much better strategy is to encrypt the data with a symmetric key, then encrypt that key with RSA. (See the end of the post for special treatment options that are especially helpful for RSA with PKCS#1 v1.5 padding.)
Working around the second problem usually requires an Authenticated Key Exchange (AKE), similar to what I covered in my Guide to End-to-End Encryption. Working around this second problem also solves the first problem, so it’s usually better to just implement a forward-secret key exchange protocol than try to make RSA secure.
(You can get forward secrecy without an AKE, by regularly rotating keys, but AKEs make forward secrecy automatic and on-by-default without forcing humans to make a decision to rotate a credential– something most people don’t do unless they have to. AKEs trade user experience complexity for protocol complexity–and this trade-off is almost universally worth taking.)
Although AKEs are extremely useful, they’re a bit complex for most software developers to pick up without prior cryptography experience. (If they were easier, after all, there wouldn’t be so much software that encrypts messages directly with RSA in the first place.)
Note: RSA itself isn’t the reason that this lacks forward secrecy. The problem is how RSA is used.
Recommendations
For Developers
First, consider not using RSA. Hell, while you’re at it, don’t write any cryptography code that you don’t have to.
Libsodium (which you should use) does most of this for you, and can easily be turned into an AKE comparable to the one Signal uses. The less cryptography code you have to write, the less can go catastrophically wrong–especially in production systems.
If jettisoning RSA from your designs is a non-starter, you should at least consider taking the Dhole Moments Pledge for Software Developers:
I will not encrypt messages directly with RSA, or any other asymmetric primitive.Simple enough, right?
Instead, if you find yourself needing to encrypt a message with RSA, remind yourself that RSA is for encrypting symmetric keys, not messages. And then plan your protocol design accordingly.
Also, I’m pretty sure RSA isn’t random-key robust. Ask your favorite cryptographer if it matters for whatever you’re building.
(But seriously, you’re better off not using RSA at all.)
For Cryptography Libraries
Let’s ask ourselves, “Why are we forcing developers to know or even care about these details?”
Libsodium doesn’t encumber developers with unnecessary decisions like this. Why does the crypto module built into JavaScript? Why does the crypto module built into most programming languages that offer one, for that matter? (Go is a notable exception here, because their security team is awesome and forward-thinking.)
In my opinion, we should stop shipping cryptography interfaces that…
- Mix symmetric and asymmetric cryptography in the same API
- Allow developers to encrypt directly with asymmetric primitives
- Force developers to manage their own nonces/initialization vectors
- Allow public/private keys to easily get confused (e.g. lack of type safety)
For example: Dhole Crypto is close to my ideal for general-purpose encryption.
Addendum: Securing RSA with PKCS#1 v1.5
Update: Neil Madden informs me that what I wrote here is actually very similar to a standard construction called RSA-KEM. You should use RSA-KEM instead of what I’ve sketched out, since that’s better studied by cryptographers.
(I’ve removed the original sketch below, to prevent accidental misuse.)
https://soatok.blog/2021/01/20/please-stop-encrypting-with-rsa-directly/
#asymmetricCryptography #cryptography #RSA #SecurityGuidance #symmetricCryptography
Governments are back on their anti-encryption bullshit again.Between the U.S. Senate’s “EARN IT” Act, the E.U.’s slew of anti-encryption proposals, and Australia’s new anti-encryption law, it’s become clear that the authoritarians in office view online privacy as a threat to their existence.
Normally, when the governments increase their anti-privacy sabre-rattling, technologists start talking more loudly about Tor, Signal, and other privacy technologies (usually only to be drowned out by paranoid people who think Tor and Signal are government backdoors or something stupid; conspiracy theories ruin everything!).
I’m not going to do that.
Instead, I’m going to show you how to add end-to-end encryption to any communication software you’re developing. (Hopefully, I’ll avoid making any bizarre design decisions along the way.)
But first, some important disclaimers:
- Yes, you should absolutely do this. I don’t care how banal your thing is; if you expect people to use it to communicate with each other, you should make it so that you can never decrypt their communications.
- You should absolutely NOT bill the thing you’re developing as an alternative to Signal or WhatsApp.
- The goal of doing this is to increase the amount of end-to-end encryption deployed on the Internet that the service operator cannot decrypt (even if compelled by court order) and make E2EE normalized. The goal is NOT to compete with highly specialized and peer-reviewed privacy technology.
- I am not a lawyer, I’m some furry who works in cryptography. The contents of this blog post is not legal advice, nor is it endorsed by any company or organization. Ask the EFF for legal questions.
The organization of this blog post is as follows: First, I’ll explain how to encrypt and decrypt data between users, assuming you have a key. Next, I’ll explain how to build an authenticated key exchange and a ratcheting protocol to determine the keys used in the first step. Afterwards, I’ll explore techniques for binding authentication keys to identities and managing trust. Finally, I’ll discuss strategies for making it impractical to ever backdoor your software (and impossible to silently backdoor it), just to piss the creeps and tyrants of the world off even more.
You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing.
(Art by Kyume.)
Preliminaries
Choosing a Cryptography Library
In the examples contained on this page, I will be using the Sodium cryptography library. Specifically, my example code will be written with the Sodium-Plus library for JavaScript, since it strikes a good balance between performance and being cross-platform.const { SodiumPlus } = require('sodium-plus');(async function() { // Select a backend automatically const sodium = await SodiumPlus.auto(); // Do other stuff here})();
Libsodium is generally the correct choice for developing cryptography features in software, and is available in most programming languages,
If you’re prone to choose a different library, you should consult your cryptographer (and yes, you should have one on your payroll if you’re doing things different) about your design choices.
Threat Modelling
Remember above when I said, “You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing”?How far you go in implementing the steps outlined on this blog post should be informed by a threat model, not an ad hoc judgment.
For example, if you’re encrypting user data and storing it in the cloud, you probably want to pass the Mud Puddle Test:
1. First, drop your device(s) in a mud puddle.
2. Next, slip in said puddle and crack yourself on the head. When you regain consciousness you’ll be perfectly fine, but won’t for the life of you be able to recall your device passwords or keys.
3. Now try to get your cloud data back.Did you succeed? If so, you’re screwed. Or to be a bit less dramatic, I should say: your cloud provider has access to your ‘encrypted’ data, as does the government if they want it, as does any rogue employee who knows their way around your provider’s internal policy checks.
Matthew Green describes the Mud Puddle Test, which Apple products definitely don’t pass.
If you must fail the Mud Puddle Test for your users, make sure you’re clear and transparent about this in the documentation for your product or service.
(Art by Swizz.)
I. Symmetric-Key Encryption
The easiest piece of this puzzle is to encrypt data in transit between both ends (thus, satisfying the loosest definition of end-to-end encryption).At this layer, you already have some kind of symmetric key to use for encrypting data before you send it, and for decrypting it as you receive it.
For example, the following code will encrypt/decrypt strings and return hexadecimal strings with a version prefix.
const VERSION = "v1";/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, key, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(50)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, key, aad ); return plaintext.toString('utf-8');}
Under-the-hood, this is using XChaCha20-Poly1305, which is less sensitive to timing leaks than AES-GCM. However, like AES-GCM, this encryption mode doesn’t provide message- or key-commitment.
If you want key commitment, you should derive two keys from
$keyusing a KDF based on hash functions: One for actual encryption, and the other as a key commitment value.If you want message commitment, you can use AES-CTR + HMAC-SHA256 or XChaCha20 + BLAKE2b-MAC.
If you want both, ask Taylor Campbell about his BLAKE3-based design.
A modified version of the above code with key-commitment might look like this:
const VERSION = "v2";/** * Derive an encryption key and a commitment hash. * @param {CryptographyKey} key * @param {Uint8Array} nonce * @returns {{encKey: CryptographyKey, commitment: Uint8Array}} */async function deriveKeys(key, nonce) { const encKey = new CryptographyKey(await sodium.crypto_generichash( new Uint8Array([0x01].append(nonce)), key )); const commitment = await sodium.crypto_generichash( new Uint8Array([0x02].append(nonce)), key ); return {encKey, commitment};}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const {encKey, commitment} = await deriveKeys(key, nonce); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, encKey, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(commitment) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(114)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const storedCommitment = await sodium.sodium_hex2bin(encrypted.slice(50, 114)); const {encKey, commitment} = await deriveKeys(key, nonce); if (!(await sodium.sodium_memcmp(storedCommitment, commitment))) { throw new Error("Incorrect commitment value"); } const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, encKey, aad ); return plaintext.toString('utf-8');}
Another design choice you might make is to encode ciphertext with base64 instead of hexadecimal. That doesn’t significantly alter the design here, but it does mean your decoding logic has to accommodate this.
You SHOULD version your ciphertexts, and include this in the AAD provided to your AEAD encryption mode. I used “v1” and “v2” as a version string above, but you can use your software name for that too.
II. Key Agreement
If you’re not familiar with Elliptic Curve Diffie-Hellman or Authenticated Key Exhcanges, the two of the earliest posts on this blog were dedicated to those topics.Key agreement in libsodium uses Elliptic Curve Diffie-Hellman over Curve25519, or X25519 for short.
There are many schools of thought for extending ECDH into an authenticated key exchange protocol.
We’re going to implement what the Signal Protocol calls X3DH instead of doing some interactive EdDSA + ECDH hybrid, because X3DH provides cryptographic deniability (see this section of the X3DH specification for more information).
For the moment, I’m going to assume a client-server model. That may or may not be appropriate for your design. You can substitute “the server” for “the other participant” in a peer-to-peer configuration.
Head’s up: This section of the blog post is code-heavy.
Update (November 23, 2020): I implemented this design in TypeScript, if you’d like something tangible to work with. I call my library, Rawr X3DH.
X3DH Pre-Key Bundles
Each participant will need to upload an Ed25519 identity key once (which is a detail covered in another section), which will be used to sign bundles of X25519 public keys to use for X3DH.Your implementation will involve a fair bit of boilerplate, like so:
/** * Generate an X25519 keypair. * * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}} */async function generateKeyPair() { const keypair = await sodium.crypto_box_keypair(); return { secretKey: await sodium.crypto_box_secretkey(keypair), publicKey: await sodium.crypto_box_publickey(keypair) };}/** * Generates some number of X25519 keypairs. * * @param {number} preKeyCount * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}[]} */async function generateBundle(preKeyCount = 100) { const bundle = []; for (let i = 0; i < preKeyCount; i++) { bundle.push(await generateKeyPair()); } return bundle;}/** * BLAKE2b( len(PK) | PK_0, PK_1, ... PK_n ) * * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function prehashPublicKeysForSigning(publicKeys) { const hashState = await sodium.crypto_generichash_init(); // First, update the state with the number of public keys const pkLen = new Uint8Array([ (publicKeys.length >>> 24) & 0xff, (publicKeys.length >>> 16) & 0xff, (publicKeys.length >>> 8) & 0xff, publicKeys.length & 0xff ]); await sodium.crypto_generichash_update(hashState, pkLen); // Next, update the state with each public key for (let pk of publicKeys) { await sodium.crypto_generichash_update( hashState, pk.getBuffer() ); } // Return the finalized BLAKE2b hash return await sodium.crypto_generichash_final(hashState);}/** * Signs a bundle. Returns the signature. * * @param {Ed25519SecretKey} signingKey * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function signBundle(signingKey, publicKeys) { return sodium.crypto_sign_detached( await prehashPublicKeysForSigning(publicKeys), signingKey );}/** * This is just so you can see how verification looks. * * @param {Ed25519PublicKey} verificationKey * @param {X25519PublicKey[]} publicKeys * @param {Uint8Array} signature */async function verifyBundle(verificationKey, publicKeys, signature) { return sodium.crypto_sign_verify_detached( await prehashPublicKeysForSigning(publicKeys), verificationKey, signature );}
This boilerplate exists just so you can do something like this:
/** * Generate some number of X25519 keypairs. * Persist the bundle. * Sign the bundle of publickeys with the Ed25519 secret key. * Return the signed bundle (which can be transmitted to the server.) * * @param {Ed25519SecretKey} signingKey * @param {number} numKeys * @returns {{signature: string, bundle: string[]}} */async function x3dh_pre_key(signingKey, numKeys = 100) { const bundle = await generateBundle(numKeys); const publicKeys = bundle.map(x => x.publicKey); const signature = await signBundle(signingKey, publicKeys); // This is a stub; how you persist it is app-specific: persistBundleNotDefinedHere(signingKey, bundle); // Hex-encode all the public keys const encodedBundle = []; for (let pk of publicKeys) { encodedBundle.push(await sodium.sodium_bin2hex(pk.getBuffer())); } return { 'signature': await sodium.sodium_bin2hex(signature), 'bundle': encodedBundle };}
And then you can drop the output of
x3dh_pre_key(secretKey)into a JSON-encoded HTTP request.In accordance to Signal’s X3DH spec, you want to use
x3dh_pre_key(secretKey, 1)to generate the “signed pre-key” bundle andx3dn_pre_key(secretKey, 100)when pushing 100 one-time keys to the server.X3DH Initiation
This section conforms to the Sending the Initial Message section of the X3DH specification.When you initiate a conversation, the server should provide you with a bundle containing:
- Your peer’s Identity key (an Ed25519 public key)
- Your peer’s current Signed Pre-Key (an X25519 public key)
- (If any remain unburned) One of your key’s One-Time Keys (an X25519 public key) — and then delete it
If we assume the structure of this response looks like this:
{ "IdentityKey": "...", "SignedPreKey": { "Signature": "..." "PreKey": "..." }, "OneTimeKey": "..." // or NULL}
Then we can write the initiation step of the handshake like so:
/** * Get SK for initializing an X3DH handshake * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} senderKey */async function x3dh_initiate_send_get_sk(r, senderKey) { const identityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey) ); const signedPreKey = new X25519PublicKey( await sodium.sodium_hex2bin(r.SignedPreKey.PreKey) ); const signature = await sodium.sodium_hex2bin(r.SignedPreKey.Signature); // Check signature const valid = await verifyBundle(identityKey, [signedPreKey], signature); if (!valid) { throw new Error("Invalid signature"); } const ephemeral = await generateKeyPair(); const ephSecret = ephemeral.secretKey; const ephPublic = ephemeral.publicKey; // Turn the Ed25519 keys into X25519 keys for X3DH: const senderX = await sodium.crypto_sign_ed25519_sk_to_curve25519(senderKey); const recipientX = await sodium.crypto_sign_ed25519_pk_to_curve25519(identityKey); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(senderX, signedPreKey); const DH2 = await sodium.crypto_scalarmult(ephSecret, recipientX); const DH3 = await sodium.crypto_scalarmult(ephSecret, signedPreKey); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( ephSecret, new X25519PublicKey(await sodium.sodium_hex2bin(r.OneTimeKey)) ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); ephSecret.wipe(); senderX.wipe(); return { IK: identityKey, EK: ephPublic, SK: SK, OTK: r.OneTimeKey // might be NULL };}/** * Initialize an X3DH handshake * * @param {string} recipientIdentity - Some identifier for the user * @param {Ed25519SecretKey} secretKey - Sender's secret key * @param {Ed25519PublicKey} publicKey - Sender's public key * @param {string} message - The initial message to send * @returns {object} */async function x3dh_initiate_send(recipientIdentity, secretKey, publicKey, message) { const r = await get_server_response(recipientIdentity); const {IK, EK, SK, OTK} = await x3dh_initiate_send_get_sk(r, secretKey); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(publicKey.getBuffer()) .concat(IK.getBuffer()) ) ); /* * We're going to set the session key for our recipient to SK. * This might invoke a ratchet. * * Either SK or the output of the ratchet derived from SK * will be returned by getEncryptionKey(). */ await setSessionKey(recipientIdentity, SK); const encrypted = await encryptData( message, await getEncryptionKey(recipientIdentity), assocData ); return { "Sender": my_identity_string, "IdentityKey": await sodium.sodium_bin2hex(publicKey), "EphemeralKey": await sodium.sodium_bin2hex(EK), "OneTimeKey": OTK, "CipherText": encrypted };}
We didn’t define
setSessionKey()orgetEncryptionKey()above. It will be covered later.X3DH – Receiving an Initial Message
This section implements the Receiving the Initial Message section of the X3DH Specification.We’re going to assume the structure of the request looks like this:
{ "Sender": "...", "IdentityKey": "...", "EphemeralKey": "...", "OneTimeKey": "...", "CipherText": "..."}
The code to handle this should look like this:
/** * Handle an X3DH initiation message as a receiver * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} identitySecret * @param {Ed25519PublicKey} identityPublic * @param {Ed25519SecretKey} preKeySecret */async function x3dh_initiate_recv_get_sk( r, identitySecret, identityPublic, preKeySecret) { // Decode strings const senderIdentityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey), ); const ephemeral = new X25519PublicKey( await sodium.sodium_hex2bin(r.EphemeralKey), ); // Ed25519 -> X25519 const senderX = await sodium.crypto_sign_ed25519_pk_to_curve25519(senderIdentityKey); const recipientX = await sodium.crypto_sign_ed25519_sk_to_curve25519(identitySecret); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(preKeySecret, senderX); const DH2 = await sodium.crypto_scalarmult(recipientX, ephemeral); const DH3 = await sodium.crypto_scalarmult(preKeySecret, ephemeral); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( await fetchAndWipeOneTimeSecretKey(r.OneTimeKey), ephemeral ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); recipientX.wipe(); return { Sender: r.Sender, SK: SK, IK: senderIdentityKey };}/** * Initiate an X3DH handshake as a recipient * * @param {object} req - Request object * @returns {string} - The initial message */async function x3dh_initiate_recv(req) { const {identitySecret, identityPublic} = await getIdentityKeypair(); const {preKeySecret, preKeyPublic} = await getPreKeyPair(); const {Sender, SK, IK} = await x3dh_initiate_recv_get_sk( req, identitySecret, identityPublic, preKeySecret, preKeyPublic ); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(IK.getBuffer()) .concat(identityPublic.getBuffer()) ) ); try { await setSessionKey(senderIdentity, SK); return decryptData( req.CipherText, await getEncryptionKey(senderIdentity), assocData ); } catch (e) { await destroySessionKey(senderIdentity); throw e; }}
And with that, you’ve successfully implemented X3DH and symmetric encryption in JavaScript.
We abstracted some of the details away (i.e.
kdf(), the transport mechanisms, the session key management mechanisms, and a few others). Some of them will be highly specific to your application, so it doesn’t make a ton of sense to flesh them out.One thing to keep in mind: According to the X3DH specification, participants should regularly (e.g. weekly) replace their Signed Pre-Key in the server with a fresh one. They should also publish more One-Time Keys when they start to run low.
If you’d like to see a complete reference implementation of X3DH, as I mentioned before, Rawr-X3DH implements it in TypeScript.
Session Key Management
Using X3DH to for every message is inefficient and unnecessary. Even the Signal Protocol doesn’t do that.Instead, Signal specifies a Double Ratchet protocol that combines a Symmetric-Key Ratchet on subsequent messages, and a Diffie-Hellman-based ratcheting protocol.
Signal even specifies integration guidelines for the Double Ratchet with X3DH.
It’s worth reading through the specification to understand their usages of Key-Derivation Functions (KDFs) and KDF Chains.
Although it is recommended to use HKDF as the Signal protocol specifies, you can strictly speaking use any secure keyed PRF to accomplish the same goal.
What follows is an example of a symmetric KDF chain that uses BLAKE2b with 512-bit digests of the current session key; the leftmost half of the BLAKE2b digest becomes the new session key, while the rightmost half becomes the encryption key.
const SESSION_KEYS = {};/** * Note: In reality you'll want to have two separate sessions: * One for receiving data, one for sending data. * * @param {string} identity * @param {CryptographyKey} key */async function setSessionKey(identity, key) { SESSION_KEYS[identity] = key;}async function getEncryptionKey(identity) { if (!SESSION_KEYS[identity]) { throw new Error("No session key for " + identity"); } const blake2bMac = await sodium.crypto_generichash( SESSION_KEYS[identity], null, 64 ); SESSION_KEYS[identity] = new CryptographyKey(blake2bMac.slice(0, 32)); return new CryptographyKey(blake2bMac.slice(32, 64));}
In the interest of time, a full DHRatchet implementation is left as an exercise to the reader (since it’s mostly a state machine), but using the appropriate functions provided by sodium-plus (
crypto_box_keypair(),crypto_scalarmult()) should be relatively straightforward.Make sure your KDFs use domain separation, as per the Signal Protocol specifications.
Group Key Agreement
The Signal Protocol specified X3DH and the Double Ratchet for securely encrypting information between two parties.Group conversations are trickier, because you have to be able to encrypt information that multiple recipients can decrypt, add/remove participants to the conversation, etc.
(The same complexity comes with multi-device support for end-to-end encryption.)
The best design I’ve read to date for tackling group key agreement is the IETF Messaging Layer Security RFC draft.
I am not going to implement the entire MLS RFC in this blog post. If you want to support multiple devices or group conversations, you’ll want a complete MLS implementation to work with.
Brief Recap
That was a lot of ground to cover, but we’re not done yet.
(Art by Khia.)
So far we’ve tackled encryption, initial key agreement, and session key management. However, we did not flesh out how Identity Keys (which are signing keys–Ed25519 specifically–rather than Diffie-Hellman keys) are managed. That detail was just sorta hand-waved until now.
So let’s talk about that.
III. Identity Key Management
There’s a meme among technology bloggers to write a post titled “Falsehoods Programmers Believe About _____”.Fortunately for us, Identity is one of the topics that furries are positioned to understand better than most (due to fursonas): Identities have a many-to-many relationship with Humans.
In an end-to-end encryption protocol, each identity will consist of some identifier (phone number, email address, username and server hostname, etc.) and an Ed25519 keypair (for which the public key will be published).
But how do you know whether or not a given public key is correct for a given identity?
This is where we segue into one of the hard problems in cryptography, where the solutions available are entirely dependent on your threat model: Public Key Infrastructure (PKI).
Some common PKI designs include:
- Certificate Authorities (CAs) — TLS does this
- Web-of-Trust (WoT) — The PGP ecosystem does this
- Trust On First Use (TOFU) — SSH does this
- Key Transparency / Certificate Transparency (CT) — TLS also does this for ensuring CA-issued certificates are auditable (although it was originally meant to replace Certificate Authorities)
And you can sort of choose-your-own-adventure on this one, depending on what’s most appropriate for the type of software you’re building and who your customers are.
One design I’m particularly fond of is called Gossamer, which is a PKI design without Certificate Authorities, originally designed for making WordPress’s automatic updates more secure (i.e. so every developer can sign their theme and plugin updates).
Since we only need to maintain an up-to-date repository of Ed25519 identity keys for each participant in our end-to-end encryption protocol, this makes Gossamer a suitable starting point.
Gossamer specifies a limited grammar of Actions that can be performed: AppendKey, RevokeKey, AppendUpdate, RevokeUpdate, and AttestUpdate. These actions are signed and published to an append-only cryptographic ledger.
I would propose a sixth action: AttestKey, so you can have WoT-like assurances and key-signing parties. (If nothing else, you should be able to attest that the identity keys of other cryptographic ledgers in the network are authentic at a point in time.)
IV. Backdoor Resistance
In the previous section, I proposed the use of Gossamer as a PKI for Identity Keys. This would provide Ed25519 keypairs for use with X3DH and the Double Ratchet, which would in turn provide session keys to use for symmetric authenticated encryption.If you’ve implemented everything preceding this section, you have a full-stack end-to-end encryption protocol. But let’s make intelligence agencies and surveillance capitalists even more mad by making it impractical to backdoor our software (and impossible to silently backdoor it).
How do we pull that off?
You want Binary Transparency.
For us, the implementation is simple: Use Gossamer as it was originally intended (i.e. to secure your software distribution channels).
Gossamer provides up-to-date verification keys and a commitment to a cryptographic ledger of every software update. You can learn more about its inspiration here.
It isn’t enough to merely use Gossamer to manage keys and update signatures. You need independent third parties to use the AttestUpdate action to assert one or more of the following:
- That builds are reproducible from the source code.
- That they have reviewed the source code and found no evidence of backdoors or exploitable vulnerabilities.
(And then you should let your users decide which of these independent third parties they trust to vet software updates.)
Closing Remarks
The U.S. Government cries and moans a lot about “criminals going dark” and wonders a lot about how to solve the “going dark problem”.If more software developers implement end-to-end encryption in their communications software, then maybe one day they won’t be able to use dragnet surveillance to spy on citizens and they’ll be forced to do actual detective work to solve actual crimes.
Y’know, like their job description actually entails?
Let’s normalize end-to-end encryption. Let’s normalize backdoor-resistant software distribution.
Let’s collectively tell the intelligence community in every sophisticated nation state the one word they don’t hear often enough:
Especially if you’re a furry. Because we improve everything! :3
Questions You Might Have
What About Private Contact Discovery?
That’s one of the major reasons why the thing we’re building isn’t meant to compete with Signal (and it MUST NOT be advertised as such):Signal is a privacy tool, and their servers have no way of identifying who can contact who.
What we’ve built here isn’t a complete privacy solution, it’s only providing end-to-end encryption (and possibly making NSA employees cry at their desk).
Does This Design Work with Federation?
Yes. Each identifier string can be [username] at [hostname].What About Network Metadata?
If you want anonymity, you want to use Tor.Why Are You Using Ed25519 Keys for X3DH?
If you only read the key agreement section of this blog post and the fact that I’m passing around Ed25519 public keys seems weird, you might have missed the identity section of this blog post where I suggested piggybacking on another protocol called Gossamer to handle the distribution of Ed25519 public keys. (Gossamer is also beneficial for backdoor resistance in software update distribution, as described in the subsequent section.)Furthermore, we’re actually using birationally equivalent X25519 keys derived from the Ed25519 keypair for the X3DH step. This is a deviation from what Signal does (using X25519 keys everywhere, then inventing an EdDSA variant to support their usage).
const publicKeyX = await sodium.crypto_sign_ed25519_pk_to_curve25519(foxPublicKey);const secretKeyX = await sodium.crypto_sign_ed25519_sk_to_curve25519(wolfSecretKey);
(Using fox/wolf instead of Alice/Bob, because it’s cuter.)
This design pattern has a few advantages:
- It makes Gossamer integration seamless, which means you can use Ed25519 for identities and still have a deniable X3DH handshake for 1:1 conversations while implementing the rest of the designs proposed.
- This approach to X3DH can be implemented entirely with libsodium functions, without forcing you to write your own cryptography implementations (i.e. for XEdDSA).
The only disadvantages I’m aware of are:
- It deviates from Signal’s core design in a subtle way that means you don’t get to claim the exact same advantages Signal does when it comes to peer review.
- Some cryptographers are distrustful of the use of birationally equivalent X25519 keys from Ed25519 keys (although there isn’t a vulnerability any of them have been able to point me to that doesn’t involve torsion groups–which libsodium’s implementation already avoids).
If these concerns are valid enough to decide against my implementation above, I invite you to talk with cryptographers about your concerns and then propose alternatives.
Has Any of This Been Implemented Already?
You can find implementations for the designs discussed on this blog post below:
- Rawr-X3DH implements X3DH in TypeScript (added 2020-11-23)
I will update this section of the blog post as implementations surface.
https://soatok.blog/2020/11/14/going-bark-a-furrys-guide-to-end-to-end-encryption/
#authenticatedEncryption #authenticatedKeyExchange #crypto #cryptography #encryption #endToEndEncryption #libsodium #OnlinePrivacy #privacy #SecurityGuidance #symmetricEncryption

Governments are back on their anti-encryption bullshit again.
Between the U.S. Senate’s “EARN IT” Act, the E.U.’s slew of anti-encryption proposals, and Australia’s new anti-encryption law, it’s become clear that the authoritarians in office view online privacy as a threat to their existence.
Normally, when the governments increase their anti-privacy sabre-rattling, technologists start talking more loudly about Tor, Signal, and other privacy technologies (usually only to be drowned out by paranoid people who think Tor and Signal are government backdoors or something stupid; conspiracy theories ruin everything!).
I’m not going to do that.
Instead, I’m going to show you how to add end-to-end encryption to any communication software you’re developing. (Hopefully, I’ll avoid making any bizarre design decisions along the way.)
But first, some important disclaimers:
- Yes, you should absolutely do this. I don’t care how banal your thing is; if you expect people to use it to communicate with each other, you should make it so that you can never decrypt their communications.
- You should absolutely NOT bill the thing you’re developing as an alternative to Signal or WhatsApp.
- The goal of doing this is to increase the amount of end-to-end encryption deployed on the Internet that the service operator cannot decrypt (even if compelled by court order) and make E2EE normalized. The goal is NOT to compete with highly specialized and peer-reviewed privacy technology.
- I am not a lawyer, I’m some furry who works in cryptography. The contents of this blog post is not legal advice, nor is it endorsed by any company or organization. Ask the EFF for legal questions.
The organization of this blog post is as follows: First, I’ll explain how to encrypt and decrypt data between users, assuming you have a key. Next, I’ll explain how to build an authenticated key exchange and a ratcheting protocol to determine the keys used in the first step. Afterwards, I’ll explore techniques for binding authentication keys to identities and managing trust. Finally, I’ll discuss strategies for making it impractical to ever backdoor your software (and impossible to silently backdoor it), just to piss the creeps and tyrants of the world off even more.
You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing.

Preliminaries
Choosing a Cryptography Library
In the examples contained on this page, I will be using the Sodium cryptography library. Specifically, my example code will be written with the Sodium-Plus library for JavaScript, since it strikes a good balance between performance and being cross-platform.
const { SodiumPlus } = require('sodium-plus');(async function() { // Select a backend automatically const sodium = await SodiumPlus.auto(); // Do other stuff here})();
Libsodium is generally the correct choice for developing cryptography features in software, and is available in most programming languages,
If you’re prone to choose a different library, you should consult your cryptographer (and yes, you should have one on your payroll if you’re doing things different) about your design choices.
Threat Modelling
Remember above when I said, “You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing”?
How far you go in implementing the steps outlined on this blog post should be informed by a threat model, not an ad hoc judgment.
For example, if you’re encrypting user data and storing it in the cloud, you probably want to pass the Mud Puddle Test:
1. First, drop your device(s) in a mud puddle.
2. Next, slip in said puddle and crack yourself on the head. When you regain consciousness you’ll be perfectly fine, but won’t for the life of you be able to recall your device passwords or keys.
3. Now try to get your cloud data back.Did you succeed? If so, you’re screwed. Or to be a bit less dramatic, I should say: your cloud provider has access to your ‘encrypted’ data, as does the government if they want it, as does any rogue employee who knows their way around your provider’s internal policy checks.
Matthew Green describes the Mud Puddle Test, which Apple products definitely don’t pass.
If you must fail the Mud Puddle Test for your users, make sure you’re clear and transparent about this in the documentation for your product or service.

I. Symmetric-Key Encryption
The easiest piece of this puzzle is to encrypt data in transit between both ends (thus, satisfying the loosest definition of end-to-end encryption).
At this layer, you already have some kind of symmetric key to use for encrypting data before you send it, and for decrypting it as you receive it.
For example, the following code will encrypt/decrypt strings and return hexadecimal strings with a version prefix.
const VERSION = "v1";/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, key, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(50)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, key, aad ); return plaintext.toString('utf-8');}
Under-the-hood, this is using XChaCha20-Poly1305, which is less sensitive to timing leaks than AES-GCM. However, like AES-GCM, this encryption mode doesn’t provide message- or key-commitment.
If you want key commitment, you should derive two keys from $key using a KDF based on hash functions: One for actual encryption, and the other as a key commitment value.
If you want message commitment, you can use AES-CTR + HMAC-SHA256 or XChaCha20 + BLAKE2b-MAC.
If you want both, ask Taylor Campbell about his BLAKE3-based design.
A modified version of the above code with key-commitment might look like this:
const VERSION = "v2";/** * Derive an encryption key and a commitment hash. * @param {CryptographyKey} key * @param {Uint8Array} nonce * @returns {{encKey: CryptographyKey, commitment: Uint8Array}} */async function deriveKeys(key, nonce) { const encKey = new CryptographyKey(await sodium.crypto_generichash( new Uint8Array([0x01].append(nonce)), key )); const commitment = await sodium.crypto_generichash( new Uint8Array([0x02].append(nonce)), key ); return {encKey, commitment};}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const {encKey, commitment} = await deriveKeys(key, nonce); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, encKey, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(commitment) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(114)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const storedCommitment = await sodium.sodium_hex2bin(encrypted.slice(50, 114)); const {encKey, commitment} = await deriveKeys(key, nonce); if (!(await sodium.sodium_memcmp(storedCommitment, commitment))) { throw new Error("Incorrect commitment value"); } const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, encKey, aad ); return plaintext.toString('utf-8');}
Another design choice you might make is to encode ciphertext with base64 instead of hexadecimal. That doesn’t significantly alter the design here, but it does mean your decoding logic has to accommodate this.
You SHOULD version your ciphertexts, and include this in the AAD provided to your AEAD encryption mode. I used “v1” and “v2” as a version string above, but you can use your software name for that too.
II. Key Agreement
If you’re not familiar with Elliptic Curve Diffie-Hellman or Authenticated Key Exhcanges, the two of the earliest posts on this blog were dedicated to those topics.
Key agreement in libsodium uses Elliptic Curve Diffie-Hellman over Curve25519, or X25519 for short.
There are many schools of thought for extending ECDH into an authenticated key exchange protocol.
We’re going to implement what the Signal Protocol calls X3DH instead of doing some interactive EdDSA + ECDH hybrid, because X3DH provides cryptographic deniability (see this section of the X3DH specification for more information).
For the moment, I’m going to assume a client-server model. That may or may not be appropriate for your design. You can substitute “the server” for “the other participant” in a peer-to-peer configuration.
Head’s up: This section of the blog post is code-heavy.
Update (November 23, 2020): I implemented this design in TypeScript, if you’d like something tangible to work with. I call my library, Rawr X3DH.
X3DH Pre-Key Bundles
Each participant will need to upload an Ed25519 identity key once (which is a detail covered in another section), which will be used to sign bundles of X25519 public keys to use for X3DH.
Your implementation will involve a fair bit of boilerplate, like so:
/** * Generate an X25519 keypair. * * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}} */async function generateKeyPair() { const keypair = await sodium.crypto_box_keypair(); return { secretKey: await sodium.crypto_box_secretkey(keypair), publicKey: await sodium.crypto_box_publickey(keypair) };}/** * Generates some number of X25519 keypairs. * * @param {number} preKeyCount * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}[]} */async function generateBundle(preKeyCount = 100) { const bundle = []; for (let i = 0; i < preKeyCount; i++) { bundle.push(await generateKeyPair()); } return bundle;}/** * BLAKE2b( len(PK) | PK_0, PK_1, ... PK_n ) * * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function prehashPublicKeysForSigning(publicKeys) { const hashState = await sodium.crypto_generichash_init(); // First, update the state with the number of public keys const pkLen = new Uint8Array([ (publicKeys.length >>> 24) & 0xff, (publicKeys.length >>> 16) & 0xff, (publicKeys.length >>> 8) & 0xff, publicKeys.length & 0xff ]); await sodium.crypto_generichash_update(hashState, pkLen); // Next, update the state with each public key for (let pk of publicKeys) { await sodium.crypto_generichash_update( hashState, pk.getBuffer() ); } // Return the finalized BLAKE2b hash return await sodium.crypto_generichash_final(hashState);}/** * Signs a bundle. Returns the signature. * * @param {Ed25519SecretKey} signingKey * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function signBundle(signingKey, publicKeys) { return sodium.crypto_sign_detached( await prehashPublicKeysForSigning(publicKeys), signingKey );}/** * This is just so you can see how verification looks. * * @param {Ed25519PublicKey} verificationKey * @param {X25519PublicKey[]} publicKeys * @param {Uint8Array} signature */async function verifyBundle(verificationKey, publicKeys, signature) { return sodium.crypto_sign_verify_detached( await prehashPublicKeysForSigning(publicKeys), verificationKey, signature );}
This boilerplate exists just so you can do something like this:
/** * Generate some number of X25519 keypairs. * Persist the bundle. * Sign the bundle of publickeys with the Ed25519 secret key. * Return the signed bundle (which can be transmitted to the server.) * * @param {Ed25519SecretKey} signingKey * @param {number} numKeys * @returns {{signature: string, bundle: string[]}} */async function x3dh_pre_key(signingKey, numKeys = 100) { const bundle = await generateBundle(numKeys); const publicKeys = bundle.map(x => x.publicKey); const signature = await signBundle(signingKey, publicKeys); // This is a stub; how you persist it is app-specific: persistBundleNotDefinedHere(signingKey, bundle); // Hex-encode all the public keys const encodedBundle = []; for (let pk of publicKeys) { encodedBundle.push(await sodium.sodium_bin2hex(pk.getBuffer())); } return { 'signature': await sodium.sodium_bin2hex(signature), 'bundle': encodedBundle };}
And then you can drop the output of x3dh_pre_key(secretKey) into a JSON-encoded HTTP request.
In accordance to Signal’s X3DH spec, you want to use x3dh_pre_key(secretKey, 1) to generate the “signed pre-key” bundle and x3dn_pre_key(secretKey, 100) when pushing 100 one-time keys to the server.
X3DH Initiation
This section conforms to the Sending the Initial Message section of the X3DH specification.
When you initiate a conversation, the server should provide you with a bundle containing:
- Your peer’s Identity key (an Ed25519 public key)
- Your peer’s current Signed Pre-Key (an X25519 public key)
- (If any remain unburned) One of your key’s One-Time Keys (an X25519 public key) — and then delete it
If we assume the structure of this response looks like this:
{ "IdentityKey": "...", "SignedPreKey": { "Signature": "..." "PreKey": "..." }, "OneTimeKey": "..." // or NULL}
Then we can write the initiation step of the handshake like so:
/** * Get SK for initializing an X3DH handshake * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} senderKey */async function x3dh_initiate_send_get_sk(r, senderKey) { const identityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey) ); const signedPreKey = new X25519PublicKey( await sodium.sodium_hex2bin(r.SignedPreKey.PreKey) ); const signature = await sodium.sodium_hex2bin(r.SignedPreKey.Signature); // Check signature const valid = await verifyBundle(identityKey, [signedPreKey], signature); if (!valid) { throw new Error("Invalid signature"); } const ephemeral = await generateKeyPair(); const ephSecret = ephemeral.secretKey; const ephPublic = ephemeral.publicKey; // Turn the Ed25519 keys into X25519 keys for X3DH: const senderX = await sodium.crypto_sign_ed25519_sk_to_curve25519(senderKey); const recipientX = await sodium.crypto_sign_ed25519_pk_to_curve25519(identityKey); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(senderX, signedPreKey); const DH2 = await sodium.crypto_scalarmult(ephSecret, recipientX); const DH3 = await sodium.crypto_scalarmult(ephSecret, signedPreKey); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( ephSecret, new X25519PublicKey(await sodium.sodium_hex2bin(r.OneTimeKey)) ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); ephSecret.wipe(); senderX.wipe(); return { IK: identityKey, EK: ephPublic, SK: SK, OTK: r.OneTimeKey // might be NULL };}/** * Initialize an X3DH handshake * * @param {string} recipientIdentity - Some identifier for the user * @param {Ed25519SecretKey} secretKey - Sender's secret key * @param {Ed25519PublicKey} publicKey - Sender's public key * @param {string} message - The initial message to send * @returns {object} */async function x3dh_initiate_send(recipientIdentity, secretKey, publicKey, message) { const r = await get_server_response(recipientIdentity); const {IK, EK, SK, OTK} = await x3dh_initiate_send_get_sk(r, secretKey); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(publicKey.getBuffer()) .concat(IK.getBuffer()) ) ); /* * We're going to set the session key for our recipient to SK. * This might invoke a ratchet. * * Either SK or the output of the ratchet derived from SK * will be returned by getEncryptionKey(). */ await setSessionKey(recipientIdentity, SK); const encrypted = await encryptData( message, await getEncryptionKey(recipientIdentity), assocData ); return { "Sender": my_identity_string, "IdentityKey": await sodium.sodium_bin2hex(publicKey), "EphemeralKey": await sodium.sodium_bin2hex(EK), "OneTimeKey": OTK, "CipherText": encrypted };}
We didn’t define setSessionKey() or getEncryptionKey() above. It will be covered later.
X3DH – Receiving an Initial Message
This section implements the Receiving the Initial Message section of the X3DH Specification.
We’re going to assume the structure of the request looks like this:
{ "Sender": "...", "IdentityKey": "...", "EphemeralKey": "...", "OneTimeKey": "...", "CipherText": "..."}
The code to handle this should look like this:
/** * Handle an X3DH initiation message as a receiver * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} identitySecret * @param {Ed25519PublicKey} identityPublic * @param {Ed25519SecretKey} preKeySecret */async function x3dh_initiate_recv_get_sk( r, identitySecret, identityPublic, preKeySecret) { // Decode strings const senderIdentityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey), ); const ephemeral = new X25519PublicKey( await sodium.sodium_hex2bin(r.EphemeralKey), ); // Ed25519 -> X25519 const senderX = await sodium.crypto_sign_ed25519_pk_to_curve25519(senderIdentityKey); const recipientX = await sodium.crypto_sign_ed25519_sk_to_curve25519(identitySecret); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(preKeySecret, senderX); const DH2 = await sodium.crypto_scalarmult(recipientX, ephemeral); const DH3 = await sodium.crypto_scalarmult(preKeySecret, ephemeral); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( await fetchAndWipeOneTimeSecretKey(r.OneTimeKey), ephemeral ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); recipientX.wipe(); return { Sender: r.Sender, SK: SK, IK: senderIdentityKey };}/** * Initiate an X3DH handshake as a recipient * * @param {object} req - Request object * @returns {string} - The initial message */async function x3dh_initiate_recv(req) { const {identitySecret, identityPublic} = await getIdentityKeypair(); const {preKeySecret, preKeyPublic} = await getPreKeyPair(); const {Sender, SK, IK} = await x3dh_initiate_recv_get_sk( req, identitySecret, identityPublic, preKeySecret, preKeyPublic ); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(IK.getBuffer()) .concat(identityPublic.getBuffer()) ) ); try { await setSessionKey(senderIdentity, SK); return decryptData( req.CipherText, await getEncryptionKey(senderIdentity), assocData ); } catch (e) { await destroySessionKey(senderIdentity); throw e; }}
And with that, you’ve successfully implemented X3DH and symmetric encryption in JavaScript.
We abstracted some of the details away (i.e. kdf(), the transport mechanisms, the session key management mechanisms, and a few others). Some of them will be highly specific to your application, so it doesn’t make a ton of sense to flesh them out.
One thing to keep in mind: According to the X3DH specification, participants should regularly (e.g. weekly) replace their Signed Pre-Key in the server with a fresh one. They should also publish more One-Time Keys when they start to run low.
If you’d like to see a complete reference implementation of X3DH, as I mentioned before, Rawr-X3DH implements it in TypeScript.
Session Key Management
Using X3DH to for every message is inefficient and unnecessary. Even the Signal Protocol doesn’t do that.
Instead, Signal specifies a Double Ratchet protocol that combines a Symmetric-Key Ratchet on subsequent messages, and a Diffie-Hellman-based ratcheting protocol.
Signal even specifies integration guidelines for the Double Ratchet with X3DH.
It’s worth reading through the specification to understand their usages of Key-Derivation Functions (KDFs) and KDF Chains.
Although it is recommended to use HKDF as the Signal protocol specifies, you can strictly speaking use any secure keyed PRF to accomplish the same goal.
What follows is an example of a symmetric KDF chain that uses BLAKE2b with 512-bit digests of the current session key; the leftmost half of the BLAKE2b digest becomes the new session key, while the rightmost half becomes the encryption key.
const SESSION_KEYS = {};/** * Note: In reality you'll want to have two separate sessions: * One for receiving data, one for sending data. * * @param {string} identity * @param {CryptographyKey} key */async function setSessionKey(identity, key) { SESSION_KEYS[identity] = key;}async function getEncryptionKey(identity) { if (!SESSION_KEYS[identity]) { throw new Error("No session key for " + identity"); } const blake2bMac = await sodium.crypto_generichash( SESSION_KEYS[identity], null, 64 ); SESSION_KEYS[identity] = new CryptographyKey(blake2bMac.slice(0, 32)); return new CryptographyKey(blake2bMac.slice(32, 64));}
In the interest of time, a full DHRatchet implementation is left as an exercise to the reader (since it’s mostly a state machine), but using the appropriate functions provided by sodium-plus (crypto_box_keypair(), crypto_scalarmult()) should be relatively straightforward.
Make sure your KDFs use domain separation, as per the Signal Protocol specifications.
Group Key Agreement
The Signal Protocol specified X3DH and the Double Ratchet for securely encrypting information between two parties.
Group conversations are trickier, because you have to be able to encrypt information that multiple recipients can decrypt, add/remove participants to the conversation, etc.
(The same complexity comes with multi-device support for end-to-end encryption.)
The best design I’ve read to date for tackling group key agreement is the IETF Messaging Layer Security RFC draft.
I am not going to implement the entire MLS RFC in this blog post. If you want to support multiple devices or group conversations, you’ll want a complete MLS implementation to work with.
Brief Recap
That was a lot of ground to cover, but we’re not done yet.

So far we’ve tackled encryption, initial key agreement, and session key management. However, we did not flesh out how Identity Keys (which are signing keys–Ed25519 specifically–rather than Diffie-Hellman keys) are managed. That detail was just sorta hand-waved until now.
So let’s talk about that.
III. Identity Key Management
There’s a meme among technology bloggers to write a post titled “Falsehoods Programmers Believe About _____”.
Fortunately for us, Identity is one of the topics that furries are positioned to understand better than most (due to fursonas): Identities have a many-to-many relationship with Humans.
In an end-to-end encryption protocol, each identity will consist of some identifier (phone number, email address, username and server hostname, etc.) and an Ed25519 keypair (for which the public key will be published).
But how do you know whether or not a given public key is correct for a given identity?
This is where we segue into one of the hard problems in cryptography, where the solutions available are entirely dependent on your threat model: Public Key Infrastructure (PKI).
Some common PKI designs include:
- Certificate Authorities (CAs) — TLS does this
- Web-of-Trust (WoT) — The PGP ecosystem does this
- Trust On First Use (TOFU) — SSH does this
- Key Transparency / Certificate Transparency (CT) — TLS also does this for ensuring CA-issued certificates are auditable (although it was originally meant to replace Certificate Authorities)
And you can sort of choose-your-own-adventure on this one, depending on what’s most appropriate for the type of software you’re building and who your customers are.
One design I’m particularly fond of is called Gossamer, which is a PKI design without Certificate Authorities, originally designed for making WordPress’s automatic updates more secure (i.e. so every developer can sign their theme and plugin updates).
Since we only need to maintain an up-to-date repository of Ed25519 identity keys for each participant in our end-to-end encryption protocol, this makes Gossamer a suitable starting point.
Gossamer specifies a limited grammar of Actions that can be performed: AppendKey, RevokeKey, AppendUpdate, RevokeUpdate, and AttestUpdate. These actions are signed and published to an append-only cryptographic ledger.
I would propose a sixth action: AttestKey, so you can have WoT-like assurances and key-signing parties. (If nothing else, you should be able to attest that the identity keys of other cryptographic ledgers in the network are authentic at a point in time.)
IV. Backdoor Resistance
In the previous section, I proposed the use of Gossamer as a PKI for Identity Keys. This would provide Ed25519 keypairs for use with X3DH and the Double Ratchet, which would in turn provide session keys to use for symmetric authenticated encryption.
If you’ve implemented everything preceding this section, you have a full-stack end-to-end encryption protocol. But let’s make intelligence agencies and surveillance capitalists even more mad by making it impractical to backdoor our software (and impossible to silently backdoor it).
How do we pull that off?
You want Binary Transparency.
For us, the implementation is simple: Use Gossamer as it was originally intended (i.e. to secure your software distribution channels).
Gossamer provides up-to-date verification keys and a commitment to a cryptographic ledger of every software update. You can learn more about its inspiration here.
It isn’t enough to merely use Gossamer to manage keys and update signatures. You need independent third parties to use the AttestUpdate action to assert one or more of the following:
- That builds are reproducible from the source code.
- That they have reviewed the source code and found no evidence of backdoors or exploitable vulnerabilities.
(And then you should let your users decide which of these independent third parties they trust to vet software updates.)
Closing Remarks
The U.S. Government cries and moans a lot about “criminals going dark” and wonders a lot about how to solve the “going dark problem”.
If more software developers implement end-to-end encryption in their communications software, then maybe one day they won’t be able to use dragnet surveillance to spy on citizens and they’ll be forced to do actual detective work to solve actual crimes.
Y’know, like their job description actually entails?
Let’s normalize end-to-end encryption. Let’s normalize backdoor-resistant software distribution.
Let’s collectively tell the intelligence community in every sophisticated nation state the one word they don’t hear often enough:
Especially if you’re a furry. Because we improve everything! :3
Questions You Might Have
What About Private Contact Discovery?
That’s one of the major reasons why the thing we’re building isn’t meant to compete with Signal (and it MUST NOT be advertised as such):
Signal is a privacy tool, and their servers have no way of identifying who can contact who.
What we’ve built here isn’t a complete privacy solution, it’s only providing end-to-end encryption (and possibly making NSA employees cry at their desk).
Does This Design Work with Federation?
Yes. Each identifier string can be [username] at [hostname].
What About Network Metadata?
If you want anonymity, you want to use Tor.
Why Are You Using Ed25519 Keys for X3DH?
If you only read the key agreement section of this blog post and the fact that I’m passing around Ed25519 public keys seems weird, you might have missed the identity section of this blog post where I suggested piggybacking on another protocol called Gossamer to handle the distribution of Ed25519 public keys. (Gossamer is also beneficial for backdoor resistance in software update distribution, as described in the subsequent section.)
Furthermore, we’re actually using birationally equivalent X25519 keys derived from the Ed25519 keypair for the X3DH step. This is a deviation from what Signal does (using X25519 keys everywhere, then inventing an EdDSA variant to support their usage).
const publicKeyX = await sodium.crypto_sign_ed25519_pk_to_curve25519(foxPublicKey);const secretKeyX = await sodium.crypto_sign_ed25519_sk_to_curve25519(wolfSecretKey);
(Using fox/wolf instead of Alice/Bob, because it’s cuter.)
This design pattern has a few advantages:
- It makes Gossamer integration seamless, which means you can use Ed25519 for identities and still have a deniable X3DH handshake for 1:1 conversations while implementing the rest of the designs proposed.
- This approach to X3DH can be implemented entirely with libsodium functions, without forcing you to write your own cryptography implementations (i.e. for XEdDSA).
The only disadvantages I’m aware of are:
- It deviates from Signal’s core design in a subtle way that means you don’t get to claim the exact same advantages Signal does when it comes to peer review.
- Some cryptographers are distrustful of the use of birationally equivalent X25519 keys from Ed25519 keys (although there isn’t a vulnerability any of them have been able to point me to that doesn’t involve torsion groups–which libsodium’s implementation already avoids).
If these concerns are valid enough to decide against my implementation above, I invite you to talk with cryptographers about your concerns and then propose alternatives.
Has Any of This Been Implemented Already?
You can find implementations for the designs discussed on this blog post below:
- Rawr-X3DH implements X3DH in TypeScript (added 2020-11-23)
I will update this section of the blog post as implementations surface.
https://soatok.blog/2020/11/14/going-bark-a-furrys-guide-to-end-to-end-encryption/
#authenticatedEncryption #authenticatedKeyExchange #crypto #cryptography #encryption #endToEndEncryption #libsodium #OnlinePrivacy #privacy #SecurityGuidance #symmetricEncryption
Zoom recently announced that they were going to make end-to-end encryption available to all of their users–not just customers.https://twitter.com/zoom_us/status/1320760108343652352
This is a good move, especially for people living in countries with inept leadership that failed to address the COVID-19 pandemic and therefore need to conduct their work and schooling remotely through software like Zoom. I enthusiastically applaud them for making this change.
End-to-end encryption, on by default, is a huge win for everyone who uses Zoom. (Art by Khia.)
The end-to-end encryption capability arrives on the heels of their acquisition of Keybase in earlier this year. Hiring a team of security experts and cryptography engineers seems like a good move overall.
Upon hearing this news, I decided to be a good neighbor and take a look at their source code, with the reasoning, “If so many people’s privacy is going to be dependent on Zoom’s security, I might as well make sure they’re not doing something ridiculously bad.”
Except I couldn’t find their source code anywhere online. But they did publish a white paper on Github…
(Art by Khia.)
Disclaimers
What follows is the opinion of some guy on the Internet with a fursona–so whether or not you choose to take it seriously should be informed by this context. It is not the opinion of anyone’s employer, nor is it endorsed by Zoom, etc. Tell your lawyers to calm their nips.More importantly, I’m not here to hate on Zoom for doing a good thing, nor on the security experts that worked hard on making Zoom better for their users. The responsibility of security professionals is to the users, after all.
Also, these aren’t zero-days, so don’t try to lecture me about “responsible” disclosure. (That term is also problematic, by the way.)
Got it? Good. Let’s move on.
(Art by Swizz.)
Bizarre Design Choices in Version 2.3 of Zoom’s E2E White Paper
Note: I’ve altered the screenshots to be white text on a black background, since my blog’s color scheme is darker than a typical academic PDF. You can find the source here.Cryptographic Algorithms
It’s a little weird that they’re calculating a signature over SHA256(Context) || SHA256(M), considering Ed25519 uses SHA512 internally.
It would make just as much sense to sign Context || M directly–or, if pre-hashing large streams is needed, SHA512(Context || M).
At the top of this section, it says it uses libsodium’s
crypto_boxinterface. But then they go onto… not actually use it.Instead, they wrote their own protocol using HKDF, two SHA256 hashes, and XChaCha20-Poly1305.
While secure, this isn’t really using the crypto_box interface.
The only part of the libsodium interface that’s being used is
[url=https://github.com/jedisct1/libsodium/blob/927dfe8e2eaa86160d3ba12a7e3258fbc322909c/src/libsodium/crypto_box/curve25519xsalsa20poly1305/box_curve25519xsalsa20poly1305.c#L35-L46]crypto_box_beforenm()[/url], which could easily have been a call tocrypto_scalarmult()instead (since they’re passing the output of the scalar multiplication to HKDF anyway).
(Art by Riley.)
Also, the SHA256(a) || SHA256(b) pattern returns. Zoom’s engineers must love SHA256 for some reason.
This time, it’s in the additional associated data for the XChaCha20-Poly1305.
Binding the ciphertext and the signature to the same context string is a sensible thing to do, it’s just the concatenation of SHA256 hashes is a bit weird when SHA512 exists.
Meeting Leader Security Code
Here we see Zoom using the a SHA256 of a constant string (“
Zoombase-1-ClientOnly-MAC-SecurityCode“) in a construction that tries but fails to be HMAC.And then they concatenate it with the SHA256 hash of the public key (which is already a 256-bit value), and then they hash the whole thing again.
It’s redundant SHA256 all the way down. The redundancy of “MAC” and “SecurityCode” in their constant string is, at least, consistent with the rest of their design philosophy.
It would be a real shame if double-hashing carried the risk of invalidating security proofs, or if the security proof for HMAC required a high Hamming distance of padding constants and this design decision also later saved HMAC from related-key attacks.
Hiding Personal Details
Wait, you’re telling me Zoom was aware of HMAC’s existence this whole time?
I give up!
Enough Pointless Dunking, What’s the Takeaway?
None of the design decisions Zoom made that I’ve criticized here are security vulnerabilities, but they do demonstrate an early lack of cryptography expertise in their product design.After all, the weirdness is almost entirely contained in section 3 of their white paper, which describes the “Phase I” of their rollout. So what I’ve pointed out here appears to be mostly legacy cruft that wasn’t risky enough to bother changing in their final design.
The rest of their paper is pretty straightforward and pleasant to read. Their design makes sense in general, and each phase includes an “Areas to Improve” section.
All in all, if you’re worried about the security of Zoom’s E2EE feature, the only thing they can really do better is to publish the source code (and link to it from the whitepaper repository for ease-of-discovery) for this feature so independent experts can publicly review it.
However, they seem to be getting a lot of mileage out of the experts on their payroll, so I wouldn’t count on that happening.
https://soatok.blog/2020/10/28/bizarre-design-choices-in-zooms-end-to-end-encryption/
#encryption #endToEndEncryption #zoom

As we look upon the sunset of a remarkably tiresome year, I thought it would be appropriate to talk about cryptographic wear-out.
What is cryptographic wear-out?
It’s the threshold when you’ve used the same key to encrypt so much data that you should probably switch to a new key before you encrypt any more. Otherwise, you might let someone capable of observing all your encrypted data perform interesting attacks that compromise the security of the data you’ve encrypted.

(Art by Swizz)
The exact value of the threshold varies depending on how exactly you’re encrypting data (n.b. AEAD modes, block ciphers + cipher modes, etc. each have different wear-out thresholds due to their composition).
Let’s take a look at the wear-out limits of the more popular symmetric encryption methods, and calculate those limits ourselves.
Specific Ciphers and Modes

Cryptographic Limits for AES-GCM
I’ve written about AES-GCM before (and why I think it sucks).
AES-GCM is a construction that combines AES-CTR with an authenticator called GMAC, whose consumption of nonces looks something like this:
- Calculating H (used in GHASH for all messages encrypted under the same key, regardless of nonce):
Encrypt(00000000 00000000 00000000 00000000)
- Calculating J0 (the pre-counter block):
- If the nonce is 96 bits long:
NNNNNNNN NNNNNNNN NNNNNNNN 00000001where theNspaces represent the nonce hexits.
- Otherwise:
s = 128 * ceil(len(nonce)/nonce) - len(nonce)
J0 = GHASH(H, nonce || zero(s+64) || int2bytes(len(nonce))
- If the nonce is 96 bits long:
- Each block of data encrypted uses J0 + block counter (starting at 1) as a CTR nonce.
- J0 is additionally used as the nonce to calculate the final GMAC tag.
AES-GCM is one of the algorithms where it’s easy to separately calculate the safety limits per message (i.e. for a given nonce and key), as well as for all messages under a key.
AES-GCM Single Message Length Limits
In the simplest case (nonce is 96 bits), you end up with the following nonces consumed:
- For each key:
00000000 00000000 00000000 00000000 - For each (nonce, key) pair:
NNNNNNNN NNNNNNNN NNNNNNNN 000000001for J0NNNNNNNN NNNNNNNN NNNNNNNN 000000002for encrypting the first 16 bytes of plaintextNNNNNNNN NNNNNNNN NNNNNNNN 000000003for the next 16 bytes of plaintext…- …
NNNNNNNN NNNNNNNN NNNNNNNN FFFFFFFFFfor the final 16 bytes of plaintext.
From here, it’s pretty easy to see that you can encrypt the blocks from 00000002 to FFFFFFFF without overflowing and creating a nonce reuse. This means that each (key, nonce) can be used to encrypt a single message up to 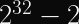
Since the block size of AES is 16 bytes, this means the maximum length of a single AES-GCM (key, nonce) pair is 
Things get a bit tricker to analyze when the nonce is not 96 bits, since it’s hashed.
The disadvantage of this hashing behavior is that it’s possible for two different nonces to produce overlapping ranges of AES-CTR output, which makes the security analysis very difficult.
However, this hashed output is also hidden from network observers since they do not know the value of H. Without some method of reliably detecting when you have an overlapping range of hidden block counters, you can’t exploit this.
(If you want to live dangerously and motivate cryptanalysis research, mix 96-bit and non-96-bit nonces with the same key in a system that does something valuable.)
Multi-Message AES-GCM Key Wear-Out
Now that we’ve established the maximum length for a single message, how many messages you can safely encrypt under a given AES-GCM key depends entirely on how your nonce is selected.
If you have a reliable counter, which is guaranteed to never repeat, and start it at 0 you can theoretically encrypt 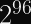

(Art by Swizz)
You probably don’t have a reliable counter, especially in real-world settings (distributed systems, multi-threaded applications, virtual machines that might be snapshotted and restored, etc.).

(Art by Swizz)
Additionally (thanks to 2adic for the expedient correction), you cannot safely encrypt more than 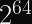
Most systems that cannot guarantee unique incrementing nonces simply generate nonces with a cryptographically secure random number generator. This is a good idea, but no matter how high quality your random number generator is, random functions will produce collisions with a discrete probability.
If you have 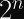
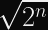
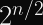
However, 50% of a nonce reuse isn’t exactly a comfortable safety threshold for most systems (especially since nonce reuse will cause AES-GCM to become vulnerable to active attackers). 1 in 4 billion is a much more comfortable safety margin against nonce reuse via collisions than 1 in 2. Fortunately, you can calculate the discrete probability of a birthday collision pretty easily.
If you want to rekey after your collision probability exceeds 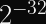
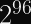
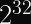
AES-GCM Safety Limits
- Maximum message length:
bytes
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
(but you probably don’t have this luxury in the real world)
- Maximum data safely encrypted under a single key with a random nonce: about
bytes

(Art by Khia.)
Cryptographic Limits for ChaCha20-Poly1305
The IETF version of ChaCha20-Poly1305 uses 96-bit nonces and 32-bit internal counters. A similar analysis follows from AES-GCM’s, with a few notable exceptions.
For starters, the one-time Poly1305 key is derived from the first 32 bytes of the ChaCha20 keystream output (block 0) for a given (nonce, key) pair. There is no equivalent to AES-GCM’s H parameter which is static for each key. (The ChaCha20 encryption begins using block 1.)
Additionally, each block for ChaCha20 is 512 bits, unlike AES’s 128 bits. So the message limit here is a little more forgiving.
Since the block size is 512 bits (or 64 bytes), and only one block is consumed for Poly1305 key derivation, we can calculate a message length limit of 
The same rules for handling 96-bit nonces applies as with AES-GCM, so we can carry that value forward.
ChaCha20-Poly1305 Safety Limits
- Maximum message length:
bytes
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
(but you probably don’t have this luxury in the real world)
- Maximum data safely encrypted under a single key with a random nonce: about
bytes

(Art by Khia.)
Cryptographic Limits for XChaCha20-Poly1305
XChaCha20-Poly1305 is a variant of XSalsa20-Poly1305 (as used in libsodium) and the IETF’s ChaCha20-Poly1305 construction. It features 192-bit nonces and 32-bit internal counters.
XChaCha20-Poly1305 is instantiated by using HChaCha20 of the key over the first 128 bits of the nonce to produce a subkey, which is used with the remaining nonce bits using the aforementioned ChaCha20-Poly1305.
This doesn’t change the maximum message length, but it does change the number of messages you can safely encrypt (since you’re actually using up to 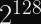
Thus, even if you manage to repeat the final ChaCha20-Poly1305 nonce, as long as the total nonce differs, each encryptions will be performed with a distinct key (thanks to the HChaCha20 key derivation; see the XSalsa20 paper and IETF RFC draft for details).
UPDATE (2021-04-15): It turns out, my read of the libsodium implementation was erroneous due to endian-ness. The maximum message length for XChaCha20-Poly1305 is 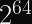
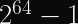
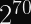
XChaCha20-Poly1305 Safety Limits
- Maximum message length:
bytes (earlier version of this document said
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
(but you probably don’t have this luxury in the real world)
- Maximum data safely encrypted under a single key with a random nonce: about
bytes

see encrypt forever, man.
(Art by Khia.)
Cryptographic Limits for AES-CBC
It’s tempting to compare non-AEAD constructions and block cipher modes such as CBC (Cipher Block Chaining), but they’re totally different monsters.
- AEAD ciphers have a clean delineation between message length limit and the message quantity limit
- CBC and other cipher modes do not have this separation
Every time you encrypt a block with AES-CBC, you are depleting from a universal bucket that affects the birthday bound security of encrypting more messages under that key. (And unlike AES-GCM with long nonces, AES-CBC’s IV is public.)
This is in addition to the operational requirements of AES-CBC (plaintext padding, initialization vectors that never repeat and must be unpredictable, separate message authentication since CBC doesn’t provide integrity and is vulnerable to chosen-ciphertext atacks, etc.).

(Art by Khia.)
For this reason, most cryptographers don’t even bother calculating the safety limit for AES-CBC in the same breath as discussing AES-GCM. And they’re right to do so!
If you find yourself using AES-CBC (or AES-CTR, for that matter), you’d best be performing a separate HMAC-SHA256 over the ciphertext (and verifying this HMAC with a secure comparison function before decrypting). Additionally, you should consider using an extended nonce construction to split one-time encryption and authentication keys.

However, for the sake of completeness, let’s figure out what our practical limits are.
CBC operates on entire blocks of plaintext, whether you need the entire block or not.
On encryption, the output of the previous block is mixed (using XOR) with the current block, then encrypted with the block cipher. For the first block, the IV is used in the place of a “previous” block. (Hence, its requirements to be non-repeating and unpredictable.)
This means you can informally model (IV xor PlaintextBlock) and (PBn xor PBn+1) as a pseudo-random function, before it’s encrypted with the block cipher.
If those words don’t mean anything to you, here’s the kicker: You can use the above discussion about birthday bounds to calculate the upper safety bounds for the total number of blocks encrypted under a single AES key (assuming IVs are generated from a secure random source).
If you’re okay with a 50% probability of a collision, you should re-key after 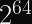
https://www.youtube.com/watch?v=v0IsYNDMV7A
If your safety margin is closer to the 1 in 4 billion (as with AES-GCM), you want to rekey after 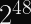
However, blocks encrypted doesn’t map neatly to bytes encrypted.
If your plaintext is always an even multiple of 128 bits (or 16 bytes), this allows for up to 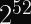
On the other extreme (1-byte plaintexts), you’ll only be able to eek 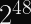
Therefore, to stay within the safety margin of AES-CBC, you SHOULD re-key after 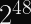
Keep in mind: 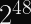
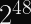
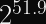
That’s Blocks. What About Bytes?
The actual plaintext byte limit sans padding is a bit fuzzy and context-dependent.
The local extrema occurs if your plaintext is always 16 bytes (and thus requires an extra 16 bytes of padding). Any less, and the padding fits within one block. Any more, and the data😛adding ratio starts to dominate.
Therefore, the worst case scenario with padding is that you take the above safety limit for block counts, and cut it in half. Cutting a number in half means reducing the exponent by 1.
But this still doesn’t eliminate the variance. 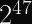
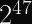
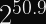
Therefore…
AES-CBC Safety Limits
- Maximum data safely encrypted under a single key with a random nonce:
bytes (approximately 141 TiB)

(Art by Khia.)
Take-Away
Compared to AES-CBC, AES-GCM gives you approximately a million times as much usage out of the same key, for the same threat profile.
ChaCha20-Poly1305 and XChaCha20-Poly1305 provides even greater allowances of encrypting data under the same key. The latter is even safe to use to encrypt arbitrarily large volumes of data under a single key without having to worry about ever practically hitting the birthday bound.
I’m aware that this blog post could have simply been a comparison table and a few footnotes (or even an IETF RFC draft), but I thought it would be more fun to explain how these values are derived from the cipher constructions.

https://soatok.blog/2020/12/24/cryptographic-wear-out-for-symmetric-encryption/
#AES #AESCBC #AESGCM #birthdayAttack #birthdayBound #cryptography #safetyMargin #SecurityGuidance #symmetricCryptography #symmetricEncryption #wearOut
There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.Today, we’re going to look at how some symmetric encryption methods stack up against each other.
If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.
Comparisons
- AES-GCM vs. ChaCha20-Poly1305
- AES-GCM vs. XChaCha20-Poly1305
- AES-GCM vs. AES-CCM
- AES-GCM vs. AES-GCM-SIV
- AES-GCM vs. AES-SIV
- AES-GCM-SIV vs. AES-SIV
- AES-GCM vs. AES-CBC
- AES-GCM vs. AES-CTR
- AES-CBC vs. AES-CTR
- AES-CBC vs. AES-ECB
- AES vs. Blowfish
- ChaCha vs. Salsa20
- ChaCha vs. RC4
- Cipher Cascades
AES-GCM vs. ChaCha20-Poly1305
- If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
- Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
- AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
- Nonce size:
- AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
- ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).
- Wearout of a single (key, nonce) pair:
- AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
- ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).
- Neither algorithm is nonce misuse resistant.
Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.
AES-GCM vs. XChaCha20-Poly1305
- XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
- To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
- The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.
Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.
AES-GCM vs. AES-CCM
AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.
Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).
A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.
Conclusion: Just use AES-GCM.
AES-GCM vs. AES-GCM-SIV
AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.
Nonce misuse resistance is really cool. (Art by Swizz)
The algorithms are significantly different:
- AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
- AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)
AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.
So really, use which ever you want.
Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?
https://twitter.com/colmmacc/status/986286693572493312
Conclusion: AES-GCM-SIV is better, but both are fine.
AES-GCM vs. AES-SIV
At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:
- Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
- AES-SIV is MAC then encrypt (so is AES-CCM).
- AES-SIV uses AES-CTR (so does AES-CCM).
If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.
AES-GCM also has the added advantage of not relying on CBC-MAC.
Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.
AES-GCM-SIV vs. AES-SIV
If you read the previous two sections, the conclusion here should be obvious.
- AES-GCM-SIV is slightly better than AES-GCM.
- AES-GCM is better than AES-SIV.
Conclusion: Use AES-GCM-SIV.
AES-GCM vs. AES-CBC
Just use AES-GCM. No contest.AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).
If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).
If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:
- encKey := HmacSha256(“encryption-cbc-hmac”, key)
- macKey := HmacSha256(“authentication-cbc-hmac”, key)
- iv := RandomBytes(16)
- ciphertext := AesCbc(plaintext, iv, encKey)
- tag := HmacSha256(iv + ciphertext, macKey)
For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.
There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.
AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.
AES-GCM vs. AES-CTR
Just use AES-GCM. No contest.Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.
If you must use AES-CTR, the same rules apply as for AES-CBC:
- encKey := HmacSha256(“encryption-ctr-hmac”, key)
- macKey := HmacSha256(“authentication-ctr-hmac”, key)
- nonce := RandomBytes(16)
- ciphertext := AesCtr(plaintext, nonce, encKey)
- tag := HmacSha256(nonce + ciphertext, macKey)
For decryption you need a secure compare function.
AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
AES-CBC vs. AES-CTR
If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.That being said:
AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.
AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.
If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.
AES-CBC vs. AES-ECB
Never use ECB mode. ECB mode lacks semantic security.Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.
Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.
AES vs. Blowfish
A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:
Why?! (Art by Khia)
Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”
Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.
AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.
AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.
Conclusion: Use AES instead of Blowfish.
ChaCha vs. Salsa20
Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.
Conclusion: Your choice (both are good but ChaCha is slightly better).
ChaCha vs. RC4
Don’t use RC4 for anything! What are you doing?
My reaction when I read that the CIA was using a modified RC4 in their Assassin malware instead of a secure stream cipher, per the Vault7 leaks. (Art by Khia)
RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.
Conclusion: Use ChaCha. Never use RC4.
Cipher Cascades
A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.
If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.
Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.
Symmetric Encryption Rankings
So with all of the above information, can we rank these algorithms into tiers?
Art by Riley
Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.
S XChaCha20-Poly1305, AES-GCM-SIV A AES-GCM, ChaCha20-Poly1305 B AES-SIV C AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2 D AES-CCM F Any: AES-ECB, RC4, Blowfish
Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaChaSoatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305

If you’re ever tasked with implementing a cryptography feature–whether a high-level protocol or a low-level primitive–you will have to take special care to ensure you’re not leaking secret information through side-channels.
The descriptions of algorithms you learn in a classroom or textbook are not sufficient for real-world use. (Yes, that means your toy RSA implementation based on GMP from your computer science 101 class isn’t production-ready. Don’t deploy it.)
But what are these elusive side-channels exactly, and how do you prevent them? And in cases where you cannot prevent them, how can you mitigate the risk to your users?

Contents
- Cryptographic Side-Channels
- Side-Channel Prevention and Mitigation
- Design Patterns for Algorithmic Constant-Time Code
- Constant-Time String Comparison
- Alternative: “Double HMAC” String Comparison
- Constant-Time Conditional Select
- Constant-Time String Inequality Comparison
- Constant-Time Integer Multiplication
- Constant-Time Integer Division
- Constant-Time Modular Inversion
- Constant-Time Null-Byte Trimming
- Further Reading and Online Resources
- Errata
Cryptographic Side-Channels
The concept of a side-channel isn’t inherently cryptographic, as Taylor Hornby demonstrates, but a side-channel can be a game over vulnerability in a system meant to maintain confidentiality (even if only for its cryptography keys).
Cryptographic side-channels allow an attacker to learn secret data from your cryptography system. To accomplish this, the attacker doesn’t necessarily study the system’s output (i.e. ciphertext); instead, they observe some other measurement, such as how much time or power was spent performing an operation, or what kind of electromagnetic radiation was emitted.
Important: While being resistant to side-channels is a prerequisite for implementations to be secure, it isn’t in and of itself sufficient for security. The underlying design of the primitives, constructions, and high-level protocols needs to be secure first, and that requires a clear and specific threat model for what you’re building.
Constant-time ECDSA doesn’t help you if you reuse k-values like it’s going out of style, but variable-time ECDSA still leaks your secret key to anyone who cares to probe your response times. Secure cryptography is very demanding.

Timing Leaks
Timing side-channels leak secrets through how much time it takes for an operation to complete.
There are many different flavors of timing leakage, including:
- Fast-failing comparison functions (memcmp() in C)
- Cache-timing vulnerabilities (e.g. software AES)
- Memory access patterns
- Conditional branches controlled by secrets
The bad news about timing leaks is that they’re almost always visible to an attacker over the network (including over the Internet (PDF)).
The good news is that most of them can be prevented or mitigated in software.

Power Usage
Different algorithms or processor operations may require different amounts of power.
For example, squaring a large number may take less power than multiplying two different large numbers. This observation has led to the development of power analysis attacks against RSA.
Power analysis is especially relevant for embedded systems and smart cards, which are easier to extract a meaningful signal from than your desktop computer.
Some information leakage through power usage can be prevented through careful engineering (for example: BearSSL, which uses Montgomery multiplication instead of square-and-multiply).
But that’s not always an option, so generally these risks are mitigated.

Electromagnetic Emissions
Your computer is a reliable source of electromagnetic emissions (such as radio waves). Some of these emissions may reveal information about your cryptographic secrets, especially to an attacker with physical proximity to your device.
The good news is that research into EM emission side-channels isn’t as mature as side-channels through timing leaks or power usage. The bad news is that mitigations for breakthroughs will generally require hardware (e.g. electromagnetic shielding).
![[Glitching] [Glitching]](https://fika.grin.hu/photo/link/10390)
Side-Channel Prevention and Mitigation
Now that we’ve established a rough sense of some of the types of side-channels that are possible, we can begin to identify what causes them and aspire to prevent the leaks from happening–and where we can’t, to mitigate the risk to a reasonable level.
Note: To be clear, I didn’t cover all of the types of side-channels.
Prevention vs. Mitigation
Preventing a side-channel means eliminating the conditions that allow the information leak to occur in the first place. For timing leaks, this means making all algorithms constant-time.
There are entire classes of side-channel leaks that aren’t possible or practical to mitigate in software. When you encounter one, the best you can hope to do is mitigate the risk.
Ideally, you want to make the attack more expensive to pull off than the reward an attacker will gain from it.
What is Constant-Time?
https://www.youtube.com/watch?v=ZD_H1ePLylA
When an implementation is said to be constant-time, what we mean is that the execution time of the code is not a function of its secret inputs.
Vulnerable AES uses table look-ups to implement the S-Box. Constant-time AES is either implemented in hardware, or is bitsliced.
Malicious Environments and Algorithmic Constant-Time
One of the greatest challenges with writing constant-time code is distinguishing between algorithmic constant-time and provably constant-time. The main difference between the two is that you cannot trust your compiler (especially a JIT compiler), which may attempt to optimize your code in a way that reintroduces the side-channel you aspired to remove.
A sufficiently advanced compiler optimization is indistinguishable from an adversary.John Regehr, possibly with apologies to Arthur C. Clarke
For compiled languages, this is a tractable but expensive problem to solve: You simply have to formally verify everything from the source code to the compiler to the silicon chips that the code will be deployed on, and then audit your supply chain to prevent malicious tampering from going undetected.
For interpreted languages (e.g. PHP and JavaScript), this formal verification strategy isn’t really an option, unless you want to formally verify the runtime that interprets scripts and prove that the operations remain constant-time on top of all the other layers of distrust.
Is this level of paranoia really worth the effort?

For that reason, we’re going to assume that algorithmic constant-time is adequate for the duration of this blog post.
If your threat model prevents you from accepting this assumption, feel free to put in the extra effort yourself and tell me how it goes. After all, as a furry who writes blog posts in my spare time for fun, I don’t exactly have the budget for massive research projects in formal verification.
Mitigation with Blinding Techniques
The best mitigation for some side-channels is called blinding: Obfuscating the inputs with some random data, then deobfuscating the outputs with the same random data, such that your keys are not revealed.
Two well-known examples include RSA decryption and Elliptic Curve Diffie-Hellman. I’ll focus on the latter, since it’s not as widely covered in the literature (although several cryptographers I’ve talked with were somehow knowledgeable about it; I suspect gatekeeping is involved).
Blinded ECDH Key Exchange
In typical ECDH implementations, you will convert a point on a Weierstrass curve 
The exact conversion formula is (
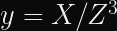
Where does 

It turns out, the choice for 
Choosing a random number means the calculations performed over Jacobian coordinates will be obscured by a randomly chosen factor 

I think it’s really cool how one small tweak to the runtime of an algorithm can make it significantly harder to attack.
Design Patterns for Algorithmic Constant-Time Code
Mitigation techniques are cool, but preventing side-channels is a better value-add for most software.
To that end, let’s look at some design patterns for constant-time software. Some of these are relatively common; others, not so much.

If you prefer TypeScript / JavaScirpt, check out Soatok’s constant-time-js library on Github / NPM.
Constant-Time String Comparison
Rather than using string comparison (== in most programming languages, memcmp() in C), you want to compare cryptographic secrets and/or calculated integrity checks with a secure compare algorithm, which looks like this:
- Initialize a variable (let’s call it D) to zero.
- For each byte of the two strings:
- Calculate (lefti XOR righti)
- Bitwise OR the current value of D with the result of the XOR, store the output in D
- When the loop has concluded, D will be equal to 0 if and only if the two strings are equal.
In code form, it looks like this:
<?phpfunction ct_compare(string $left, string $right): bool{ $d = 0; $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { return false; // Lengths differ } for ($i = 0; $i < $length; ++$i) { $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $d |= ($leftCharCode ^ $rightCharCode); } return $d === 0;}
In this example, I’m using PHP’s unpack() function to avoid cache-timing leaks with ord() and chr(). Of course, you can simply use hash_equals() instead of writing it yourself (PHP 5.6.0+).
Alternative: “Double HMAC” String Comparison
If the previous algorithm won’t work (i.e. because you’re concerned your JIT compiler will optimize it away), there is a popular alternative to consider. It’s called “Double HMAC” because it was traditionally used with Encrypt-Then-HMAC schemes.
The algorithm looks like this:
- Generate a random 256-bit key, K. (This can be cached between invocations, but it should be unpredictable.)
- Calculate HMAC-SHA256(K, left).
- Calculate HMAC-SHA256(K, right).
- Return true if the outputs of step 2 and 3 are equal.
This is provably secure, so long as HMAC-SHA256 is a secure pseudo-random function and the key K is unknown to the attacker.
In code form, the Double HMAC compare function looks like this:
<?phpfunction hmac_compare(string $left, string $right): bool{ static $k = null; if (!$k) $k = random_bytes(32); return ( hash_hmac('sha256', $left, $k) === hash_hmac('sha256', $right, $k) );}
Constant-Time Conditional Select
I like to imagine a conversation between a cryptography engineer and a Zen Buddhist, that unfolds like so:
- CE: “I want to eliminate branching side-channels from my code.”
- ZB: “Then do not have branches in your code.”
And that is precisely what we intend to do with a constant-time conditional select: Eliminate branches by conditionally returning between one of two strings, without an IF statement.

This isn’t as tricky as it sounds. We’re going to use XOR and two’s complement to achieve this.
The algorithm looks like this:
- Convert the selection bit (TRUE/FALSE) into a mask value (-1 for TRUE, 0 for FALSE). Bitwise, -1 looks like 111111111…1111111111, while 0 looks like 00000000…00000000.
- Copy the right string into a buffer, call it tmp.
- Calculate left XOR right, call it x.
- Return (tmp XOR (x AND mask)).
Once again, in code this algorithm looks like this:
<?phpfunction ct_select( bool $returnLeft, string $left, string $right): string { $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } // Mask byte $mask = (-$returnLeft) & 0xff; // X $x = (string) ($left ^ $right); // Output = Right XOR (X AND Mask) $output = ''; for ($i = 0; $i < $length; $i++) { $rightCharCode = unpack('C', $right[$i])[1]; $xCharCode = unpack('C', $x[$i])[1]; $output .= pack( 'C', $rightCharCode ^ ($xCharCode & $mask) ); } return $output;}
You can test this code for yourself here. The function was designed to read intuitively like a ternary operator.
A Word of Caution on Cleverness
In some languages, it may seem tempting to use the bitwise trickery to swap out pointers instead of returning a new buffer. But do not fall for this Siren song.
If, instead of returning a new buffer, you just swap pointers, what you’ll end up doing is creating a timing leak through your memory access patterns. This can culminate in a timing vulnerability, but even if your data is too big to fit in a processor’s cache line (I dunno, Post-Quantum RSA keys?), there’s another risk to consider.
Virtual memory addresses are just beautiful lies. Where your data lives on the actual hardware memory is entirely up to the kernel. You can have two blobs with contiguous virtual memory addresses that live on separate memory pages, or even separate RAM chips (if you have multiple).
If you’re swapping pointers around, and they point to two different pieces of hardware, and one is slightly faster to read from than the other, you can introduce yet another timing attack through which pointer is being referenced by the processor.

If you’re swapping between X and Y before performing a calculation, where:
- X lives on RAM chip 1, which takes 3 ns to read
- Y lives on RAM chip 2, which takes 4 ns to read
…then the subsequent use of the swapped pointers reveals whether you’re operating on X or Y in the timing: It will take slightly longer to read from Y than from X.
The best way to mitigate this problem is to never design your software to have it in the first place. Don’t be clever on this one.
Constant-Time String Inequality Comparison
Sometimes you don’t just need to know if two strings are equal, you also need to know which one is larger than the other.
To accomplish this in constant-time, we need to maintain two state variables:
- gt (initialized to 0, will be set to 1 at some point if left > right)
- eq (initialized to 1, will be set to 0 at some point if left != right)
Endian-ness will dictate the direction our algorithm goes, but we’re going to perform two operations in each cycle:
- gt should be bitwise ORed with (eq AND ((right – left) right shifted 8 times)
- eq should be bitwise ANDed with ((right XOR left) – 1) right shifted 8 times
If right and left are ever different, eq will be set to 0.
If the first time they’re different the value for lefti is greater than the value for righti, then the subtraction will produce a negative number. Right shifting a negative number 8 places then bitwise ANDing the result with eq (which is only 1 until two bytes differ, and then 0 henceforth if they do) will result in a value for 1 with gt. Thus, if (righti – lefti) is negative, gt will be set to 1. Otherwise, it remains 0.
At the end of this loop, return (gt + gt + eq) – 1. This will result in the following possible values:
- left < right: -1
- left == right: 0
- left > right: 1
The arithmetic based on the possible values of gt and eq should be straightforward.
- Different (eq == 0) but not greater (gt == 0) means left < right, -1.
- Different (eq == 0) and greater (gt == 1) means left > right, 1.
- If eq == 1, no bytes ever differed, so left == right, 0.
A little endian implementation is as follows:
<?phpfunction str_compare(string $left, string $right): int{ $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } $gt = 0; $eq = 1; $i = $length; while ($i > 0) { --$i; $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $gt |= (($rightCharCode - $leftCharCode) >> 8) & $eq; $eq &= (($rightCharCode ^ $leftCharCode) -1) >> 8; } return ($gt + $gt + $eq) - 1;}
Demo for this function is available here.
Constant-Time Integer Multiplication
Multiplying two integers is one of those arithmetic operations that should be constant-time. But on many older processors, it isn’t.

Fortunately, there is a workaround. It involves an algorithm called Ancient Egyptian Multiplication in some places or Peasant Multiplication in others.
Multiplying two numbers 
- Determine the number of operations you need to perform. Generally, this is either known ahead of time or
.
- Set
to 0.
- Until the operation count reaches zero:
- If the lowest bit of
is set, add
to
.
- Left shift
by 1.
- Right shfit
by 1.
- If the lowest bit of
- Return
.
The main caveat here is that you want to use bitwise operators in step 3.1 to remove the conditional branch.
Rather than bundle example code in our blog post, please refer to the implementation in sodium_compat (a pure PHP polyfill for libsodium).
For big number libraries, implementing Karatsuba on top of this integer multiplying function should be faster than attempting to multiply bignums this way.
Constant-Time Integer Division
Although some cryptography algorithms call for integer division, division isn’t usually expected to be constant-time.
However, if you look up a division algorithm for unsigned integers with a remainder, you’ll likely encounter this algorithm, which is almost constant-time:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator if R ≥ D then R := R − D Q(i) := 1 endend
If we use the tricks we learned from implementing constant-time string inequality with constant-time conditional selection, we can implement this algorithm without timing leaks.
Our constant-time version of this algorithm looks like this:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator compared := ct_compare(R, D) -- Use constant-time inequality -- if R > D then compared == 1, swap = 1 -- if R == D then compared == 0, swap = 1 -- if R < D then compared == -1, swap = 0 swap := (1 - ((compared >> 31) & 1)) -- R' = R - D -- Q' = Q, Q = 1 Rprime := R - D Qprime := Q Qprime(i) := 1 -- The i'th bit is set to 1 -- Replace (R with R', Q with Q') if swap == 1 R = ct_select(swap, Rprime, R) Q = ct_select(swap, Qprime, Q)end
It’s approximately twice as slow as the original, but it’s constant-time.

Constant-Time Modular Inversion
Modular inversion is the calculation of 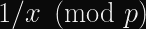
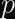
Daniel J. Bernstein and Bo-Yin Yang published a paper on fast constant-time GCD and Modular Inversion in 2019. The algorithm in question is somewhat straightforward to implement (although determining whether or not that implementation is safe is left as an exercise to the rest of us).
A simpler technique is to use Fermat’s Little Theorem: 
BearSSL provides an implementation (and accompanying documentation) for a constant-time modular inversion algorithm based on Binary GCD.
(In the future, I may update this section of this blog post with an implementation in PHP, using the GMP extension.)
Constant-Time Null-Byte Trimming
Shortly after this guide first went online, security researchers published the Raccoon Attack, which used a timing leak in the number of leading 0 bytes in the pre-master secret–combined with a lattice attack to solve the hidden number problem–to break TLS-DH(E).
To solve this, you need two components:
- A function that returns a slice of an array without timing leaks.
- A function that counts the number of significant bytes (i.e. ignores leading zero bytes, counts from the first non-zero byte).
A timing-safe array resize function needs to do two things:
- Touch every byte of the input array once.
- Touch every byte of the output array at least once, linearly. The constant-time division algorithm is useful here (to calculate x mod n for the output array index).
- Conditionally select between input[x] and the existing output[x_mod_n], based on whether x >= target size.
I’ve implemented this in my constant-time-js library:
Further Reading and Online Resources
If you’re at all interested in cryptographic side-channels, your hunger for knowledge probably won’t be sated by a single blog post. Here’s a collection of articles, papers, books, etc. worth reading.
- BearSSL’s Documentation on Constant-Time Code — A must-read for anyone interested in this topic
- Cryptographically Secure PHP Development — How to write secure cryptography in languages that cryptographers largely neglect
- CryptoCoding — A style guide for writing secure cryptography code in C (with example code!)
- CryptoGotchas — An overview of the common mistakes one can make when writing cryptography code (which is a much wider scope than side-channels)
- Meltdown and Spectre — Two vulnerabilities that placed side-channels in the scope of most of infosec that isn’t interested in cryptography
- Serious Cryptography — For anyone who lacks the background knowledge to fully understand what I’m talking about on this page
Errata
- 2020-08-27: The original version of this blog post incorrectly attributed Jacobian coordinate blinding to ECDSA hardening, rather than ECDH hardening. This error was brought to my attention by Thai Duong. Thanks Thai!
- 2020-08-27: Erin correctly pointed out that omitting memory access timing was a disservice to developers, who might not be aware of the risks involved. I’ve updated the post to call this risk out specifically (especially in the conditional select code, which some developers might try to implement with pointer swapping without knowing the risks involved). Thanks Erin!
I hope you find this guide to side-channels helpful.

Follow my blog for more Defense Against the Bark Arts posts in the future.
https://soatok.blog/2020/08/27/soatoks-guide-to-side-channel-attacks/
#asymmetricCryptography #constantTime #cryptography #ECDH #ECDSA #ellipticCurveCryptography #RSA #SecurityGuidance #sideChannels #symmetricCryptography
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Art by Khia.
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting
(at 50% probability) blocks.
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
you expect from AES.
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.This is because Grover’s quantum search algorithm can search
unsorted items in
time, which can be used to reduce the total number of possible secrets from
to
. This effectively cuts the security level, expressed in bits, in half.
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
(plaintext, key) pairs that produce any given ciphertext block.
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
times as many AES-256 keys as there are possible plaintext/ciphertexts. Keep this in mind for AES-GCM.
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
This is unacceptable!
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
: A number that must only be used once).
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
The deeper you look into AES-GCM’s design, the harder you will feel this sticker.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called. This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
This is often sold as an advantage: Reusingallows for better performance. However, it makes GCM brittle: Reusing a nonce allows an attacker to recover H and then forge messages forever. This is called the “forbidden attack”, and led to real world practical breaks.
Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.If we assume AES is well-behaved, we can deduce that there are approximately
different 256-bit keys that will map a single plaintext block to a single ciphertext block.
This is trivial to calculate. Simply divide the number of possible keys (
) by the number of possible block states (
) to yield the number of keys that produce a given ciphertext for a single block of plaintext:
.
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
.
This means there are approximately
independent keys that will map a given all-zero plaintext block to an arbitrarily chosen value of
(if we assume AES doesn’t have weird biases).
Credit: Harubaki
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection ofas a 128-bit pseudorandom function, rather than a 128-bit permutation. As a result, you an expect a collision with 50% probability after only
different keys are selected.
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a
collision risk. So that means our safety limit is actually
different AES keys before you have to worry about
reuse.
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of
different AES keys, you have to either accept the risk or stop using AES-GCM.
If you have a billion users (
), the safety limit is breached after
AES keys per user (approximately 262,000).
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.is used for block multiplication, and
(the value of
with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.
The arrow highlighted with green is HF.
It’s tempting to think that a reuse of
isn’t a concern because
will necessarily be randomized, which prevents an attacker from observing when
collides. It’s certainly true that the single-block collision risk discussed previously for
will almost certainly not also result in a collision for
. And since
isn’t reused unless a nonce is reused (which also leaks
directly), this might seem like a non-issue.
Art by Khia.
However, it’s straightforward to go from a condition of
reuse to an adaptive chosen-ciphertext attack.
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- Use your knowledge of
, the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of
for a given nonce.
- Calculate a new authentication tag for a chosen ciphertext using
and your candidate
value, then replay it into the target system.
While the blinding offered by XORing the final output with
is sufficient to stop
from being leaked directly, the protection is one-way.
Ergo, a collision in
is not sufficiently thwarted by
.
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
is
, and finding an untargeted collision requires being able to observe more than
different sessions, and somehow distinguish when
collides.
As a user, you know that after
different keys, you’ve crossed the safety boundary for avoiding
collisions. But as an attacker, you need
bites at the apple, not
. Additionally, you need some sort of oracle or distinguisher for when this happens.
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
is challenging to work with. You would need the computational and data storages of a major cloud service provider to even think about pulling the attack off.
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
bytes long, under a given (key, nonce) pair.
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
messages.
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atrandom nonces, which represents a collision probability of one in 4 billion.
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
I’m glad you asked!
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
messages (for the same collision probability as AES-GCM).
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography

There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.
Today, we’re going to look at how some symmetric encryption methods stack up against each other.
If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.
Comparisons
- AES-GCM vs. ChaCha20-Poly1305
- AES-GCM vs. XChaCha20-Poly1305
- AES-GCM vs. AES-CCM
- AES-GCM vs. AES-GCM-SIV
- AES-GCM vs. AES-SIV
- AES-GCM-SIV vs. AES-SIV
- AES-GCM vs. AES-CBC
- AES-GCM vs. AES-CTR
- AES-CBC vs. AES-CTR
- AES-CBC vs. AES-ECB
- AES vs. Blowfish
- ChaCha vs. Salsa20
- ChaCha vs. RC4
- Cipher Cascades
AES-GCM vs. ChaCha20-Poly1305
- If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
- Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
- AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
- Nonce size:
- AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
- ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).
- Wearout of a single (key, nonce) pair:
- AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
- ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).
- Neither algorithm is nonce misuse resistant.
Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.
AES-GCM vs. XChaCha20-Poly1305
- XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
- To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
- The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.
Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.
AES-GCM vs. AES-CCM
AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.
Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.
Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).
A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.
Conclusion: Just use AES-GCM.
AES-GCM vs. AES-GCM-SIV
AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.

The algorithms are significantly different:
- AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
- AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)
AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.
So really, use which ever you want.
Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?
https://twitter.com/colmmacc/status/986286693572493312
Conclusion: AES-GCM-SIV is better, but both are fine.
AES-GCM vs. AES-SIV
At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:
- Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
- AES-SIV is MAC then encrypt (so is AES-CCM).
- AES-SIV uses AES-CTR (so does AES-CCM).
If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.
AES-GCM also has the added advantage of not relying on CBC-MAC.
Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.
AES-GCM-SIV vs. AES-SIV
If you read the previous two sections, the conclusion here should be obvious.
- AES-GCM-SIV is slightly better than AES-GCM.
- AES-GCM is better than AES-SIV.
Conclusion: Use AES-GCM-SIV.
AES-GCM vs. AES-CBC
Just use AES-GCM. No contest.
AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).
If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).
If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:
- encKey := HmacSha256(“encryption-cbc-hmac”, key)
- macKey := HmacSha256(“authentication-cbc-hmac”, key)
- iv := RandomBytes(16)
- ciphertext := AesCbc(plaintext, iv, encKey)
- tag := HmacSha256(iv + ciphertext, macKey)
For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.
There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.
AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.
AES-GCM vs. AES-CTR
Just use AES-GCM. No contest.
Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.
If you must use AES-CTR, the same rules apply as for AES-CBC:
- encKey := HmacSha256(“encryption-ctr-hmac”, key)
- macKey := HmacSha256(“authentication-ctr-hmac”, key)
- nonce := RandomBytes(16)
- ciphertext := AesCtr(plaintext, nonce, encKey)
- tag := HmacSha256(nonce + ciphertext, macKey)
For decryption you need a secure compare function.
AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
AES-CBC vs. AES-CTR
If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.
That being said:
AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.
AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.
If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.
AES-CBC vs. AES-ECB
Never use ECB mode. ECB mode lacks semantic security.
Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.
Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.
AES vs. Blowfish
A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:

Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”
Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.
AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.
AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.
Conclusion: Use AES instead of Blowfish.
ChaCha vs. Salsa20
Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.
That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.
Conclusion: Your choice (both are good but ChaCha is slightly better).
ChaCha vs. RC4
Don’t use RC4 for anything! What are you doing?

RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.
Conclusion: Use ChaCha. Never use RC4.
Cipher Cascades
A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).
Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.
If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.
Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.
Symmetric Encryption Rankings
So with all of the above information, can we rank these algorithms into tiers?

Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.
| S | XChaCha20-Poly1305, AES-GCM-SIV |
| A | AES-GCM, ChaCha20-Poly1305 |
| B | AES-SIV |
| C | AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2 |
| D | AES-CCM |
| F | Any: AES-ECB, RC4, Blowfish Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaCha |
Soatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/
#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305
Authenticated Key Exchanges are an interesting and important building block in any protocol that aims to allow people to communicate privately over an untrusted medium (i.e. the Internet).What’s an AKE?
At their core, Authenticated Key Exchanges (AKEs for short) combine two different classes of protocol.
- An authentication mechanism, such as a MAC or a digital signature.
- Key encapsulation, usually through some sort of Diffie-Hellman.
A simple example of an AKE is the modern TLS handshake, which uses digital signatures (X.509 certificates signed by certificate authorities) to sign ephemeral Elliptic Curve Diffie-Hellman (ECDH) public keys, which is then used to derive a shared secret to encrypt and authenticate network traffic.
I guess I should say “simple” with scare quotes. Cryptography is very much a “devil’s in the details” field, because my above explanation didn’t even encapsulate mutual-auth TLS or the underlying machinery of protocol negotiation. (Or the fact that non-forward-secret ciphersuites can be selected.)
AKEs get much more complicated, the more sophisticated your threat model becomes.
For example: Signal’s X3DH and Double Ratchet protocols are components of a very sophisticated AKE. Learn more about them here.
The IETF is working to standardize their own approach, called Messaging Layer Security (MLS), which uses a binary tree of ECDH handshakes to manage state and optimize group operations (called TreeKEM). You can learn more about IETF MLS here.
Password AKEs
Recently, a collection of cryptographers at the IETF’s Crypto Research Forum Group (CFRG) decided to hammer on a series of proposed Password-Authenticated Key Exchange (PAKE) protocols.PAKEs come in two flavors: Balanced (mutually authenticated) and augmented (one side is a prover, the other is a verifier). Balanced PAKEs are good for encrypted tunnels where you control both endpoints (e.g. WiFi networks), whereas Augmented PAKEs are great for eliminating the risk of password theft in client-server applications, if the server gets hacked.
Ultimately, the CFRG settled on one balanced PAKE (CPace) and one augmented PAKE (OPAQUE).
Consequently, cryptographer Filippo Valsorda managed to implement CPace in 125 lines of Go, using Ristretto255.
I implemented the CPace PAKE yesterday with Go and ristretto255, and it felt like cheating.125 lines of code! Really happy with it and it was a lot of fun.
— Filippo Valsorda (@FiloSottile) March 29, 2020
Why So Complicated?
At the end of the day, an AKE is just a construction that combines key encapsulation with an authentication mechanism.But how you combine these components together can vary wildly!
Some AKE designs (i.e. Dragonfly, in WPA3) are weaker than others; even if only in the sense of being difficult to implement in constant-time.
The reason there’s so many is that cryptographers tend to collectively decide which algorithms to recommend for standardization.
(n.b. There are a lot more block ciphers than DES, Blowfish, and AES to choose from! But ask a non-cryptographer to name five block ciphers and they’ll probably struggle.)
https://soatok.blog/2020/04/21/authenticated-key-exchanges/
#ake #authenticatedKeyExchange #cryptography #ECDH

If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.
I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.
In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.
Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks

Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).
There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.
Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting 
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the 
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.
This is because Grover’s quantum search algorithm can search 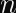
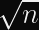
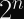
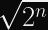
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately 
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are 
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.
Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.

Art by Swizz.
However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.

What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.
AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
: A number that must only be used once).
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.

GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called 
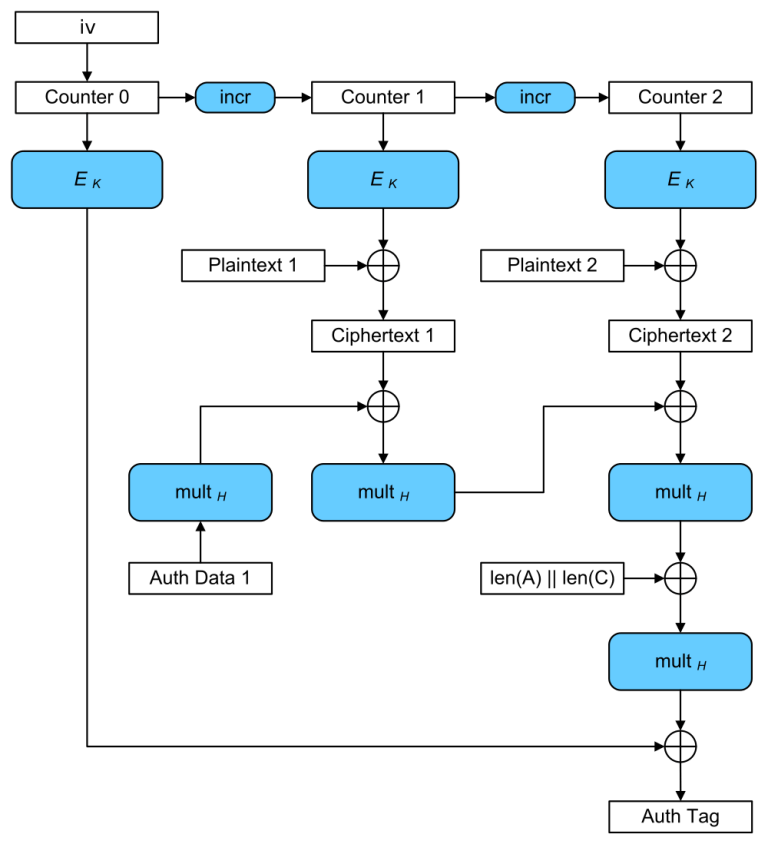
This is often sold as an advantage: Reusing 
Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.
If we assume AES is well-behaved, we can deduce that there are approximately 
This is trivial to calculate. Simply divide the number of possible keys (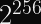


Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately 
This means there are approximately 


“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection of 
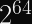
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a 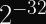
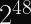

This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of 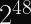
If you have a billion users (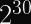
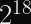
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key. 
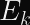
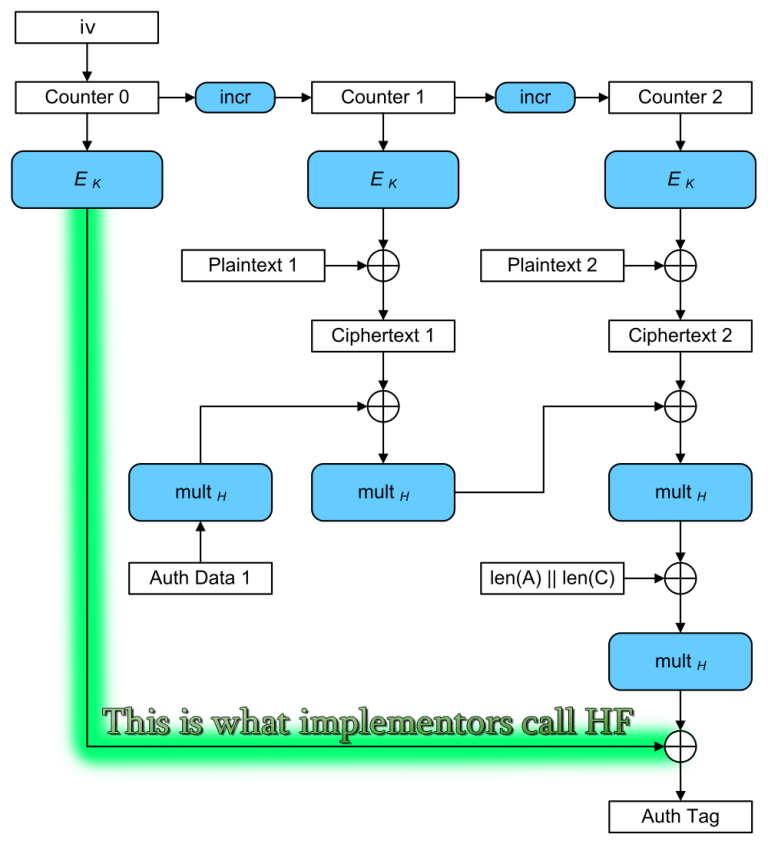
It’s tempting to think that a reuse of 




However, it’s straightforward to go from a condition of 
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- e.g. Multiple JWTs encrypted with
- Use your knowledge of
, the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of
for a given nonce.
- Calculate a new authentication tag for a chosen ciphertext using
and your candidate
value, then replay it into the target system.
While the blinding offered by XORing the final output with 

Ergo, a collision in 
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.
If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.
Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in 

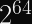

As a user, you know that after 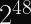

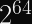
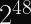
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide 
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.
(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
bytes long, under a given (key, nonce) pair.
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
messages.
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atrandom nonces, which represents a collision probability of one in 4 billion.
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).
You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”

XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
messages (for the same collision probability as AES-GCM).
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.
Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.
Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography
There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.Today, we’re going to look at how some symmetric encryption methods stack up against each other.
If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.
Comparisons
- AES-GCM vs. ChaCha20-Poly1305
- AES-GCM vs. XChaCha20-Poly1305
- AES-GCM vs. AES-CCM
- AES-GCM vs. AES-GCM-SIV
- AES-GCM vs. AES-SIV
- AES-GCM-SIV vs. AES-SIV
- AES-GCM vs. AES-CBC
- AES-GCM vs. AES-CTR
- AES-CBC vs. AES-CTR
- AES-CBC vs. AES-ECB
- AES vs. Blowfish
- ChaCha vs. Salsa20
- ChaCha vs. RC4
- Cipher Cascades
AES-GCM vs. ChaCha20-Poly1305
- If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
- Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
- AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
- Nonce size:
- AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
- ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).
- Wearout of a single (key, nonce) pair:
- AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
- ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).
- Neither algorithm is nonce misuse resistant.
Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.
AES-GCM vs. XChaCha20-Poly1305
- XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
- To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
- The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.
Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.
AES-GCM vs. AES-CCM
AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.
Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).
A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.
Conclusion: Just use AES-GCM.
AES-GCM vs. AES-GCM-SIV
AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.
Nonce misuse resistance is really cool. (Art by Swizz)
The algorithms are significantly different:
- AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
- AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)
AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.
So really, use which ever you want.
Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?
https://twitter.com/colmmacc/status/986286693572493312
Conclusion: AES-GCM-SIV is better, but both are fine.
AES-GCM vs. AES-SIV
At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:
- Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
- AES-SIV is MAC then encrypt (so is AES-CCM).
- AES-SIV uses AES-CTR (so does AES-CCM).
If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.
AES-GCM also has the added advantage of not relying on CBC-MAC.
Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.
AES-GCM-SIV vs. AES-SIV
If you read the previous two sections, the conclusion here should be obvious.
- AES-GCM-SIV is slightly better than AES-GCM.
- AES-GCM is better than AES-SIV.
Conclusion: Use AES-GCM-SIV.
AES-GCM vs. AES-CBC
Just use AES-GCM. No contest.AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).
If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).
If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:
- encKey := HmacSha256(“encryption-cbc-hmac”, key)
- macKey := HmacSha256(“authentication-cbc-hmac”, key)
- iv := RandomBytes(16)
- ciphertext := AesCbc(plaintext, iv, encKey)
- tag := HmacSha256(iv + ciphertext, macKey)
For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.
There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.
AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.
AES-GCM vs. AES-CTR
Just use AES-GCM. No contest.Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.
If you must use AES-CTR, the same rules apply as for AES-CBC:
- encKey := HmacSha256(“encryption-ctr-hmac”, key)
- macKey := HmacSha256(“authentication-ctr-hmac”, key)
- nonce := RandomBytes(16)
- ciphertext := AesCtr(plaintext, nonce, encKey)
- tag := HmacSha256(nonce + ciphertext, macKey)
For decryption you need a secure compare function.
AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
AES-CBC vs. AES-CTR
If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.That being said:
AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.
AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.
If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.
AES-CBC vs. AES-ECB
Never use ECB mode. ECB mode lacks semantic security.Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.
Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.
AES vs. Blowfish
A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:
Why?! (Art by Khia)
Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”
Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.
AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.
AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.
Conclusion: Use AES instead of Blowfish.
ChaCha vs. Salsa20
Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.
Conclusion: Your choice (both are good but ChaCha is slightly better).
ChaCha vs. RC4
Don’t use RC4 for anything! What are you doing?
My reaction when I read that the CIA was using a modified RC4 in their Assassin malware instead of a secure stream cipher, per the Vault7 leaks. (Art by Khia)
RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.
Conclusion: Use ChaCha. Never use RC4.
Cipher Cascades
A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.
If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.
Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.
Symmetric Encryption Rankings
So with all of the above information, can we rank these algorithms into tiers?
Art by Riley
Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.
S XChaCha20-Poly1305, AES-GCM-SIV A AES-GCM, ChaCha20-Poly1305 B AES-SIV C AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2 D AES-CCM F Any: AES-ECB, RC4, Blowfish
Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaChaSoatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305