Search
Items tagged with: digitalSignatureAlgorithm
Earlier this year, Cendyne published A Deep Dive into Ed25519 Signatures, which covered some of the different types of digital signature algorithms, but mostly delved into the Ed25519 algorithm. Truth in advertising.
This got me thinking, “Why isn’t there a better comparison of different elliptic curve signature algorithms available online?”

Most people just defer to SafeCurves, but it’s a little dated: We have complete addition formulas for Weierstrass curves now, but SafeCurves doesn’t reflect that.
For the purpose of simplicity, I’m not going to focus on a general treatment of Elliptic Curve Cryptography (ECC), which includes pairing-based cryptography, Elliptic-Curve Diffie-Hellman, and (arguably) isogeny cryptography.
Instead, I’m going to focus entirely on elliptic curve digital signature algorithms.
Note: The content of this post is a bit lower-level than most programmers ever need to be concerned with. If you’re a programmer and interested in learning cryptography, start here. If you’re looking for library recommendations, libsodium is a good safe default.
Compliance Rules Everything Around Me
If you have to meet some arbitrary compliance requirements (i.e. FIPS 140-3, CNSA, etc.), your decision is already made for you, and you shouldn’t waste your time reading blogs like this that will only get your hopes up about the options available to you.
Choose the option your compliance officer demands, and hope it’s good enough.

Art: LvJ
Elliptic Curves for Signature Algorithms
Let’s start with the same curve Cendyne analyzed: Ed25519.
Ed25519 (EdDSA, Curve25519)
Ed25519 is one of the two digital signature algorithms today that use the EdDSA algorithm framework. The other is Ed448, which targets a higher security level (224-bit vs 128-bit) but is also slower and uses SHAKE256 (which is overkill and not great for performance).
Ed25519 is a safe default choice for most applications where a digital signature is appropriate, for many reasons:
- Ed25519 uses deterministic nonces, which means you’re severely unlikely to ever reproduce the Sony ECDSA k-reuse bug in your system.
The deterministic nonce is calculated from the SHA512 hash of the secret key and message. Two invocations tocrypto_sign_ed25519()with the same message and secret key will produce the same signature, but the intermediate nonce value is never revealed to an attacker. - Ed25519 includes the public key in the data hashed to produce the signature (more specifically s from the (R,s) pair). This offers a property that ECDSA lacks: Exclusive Ownership. I’ve written about this property before.
Without Exclusive Ownership, it’s possible to create a single signature value that’s valid for multiple different (message, public key) pairs.
Years ago, there would have an additional list item: Ed25519 uses Edward Curves, which have complete addition formulas and are therefore safer to implement in constant-time than Weierstrass curves (i.e. the NIST curves). However, we now have complete addition formulas for Weierstrass curves, so this has become a moot point (assuming your implementation uses complete addition formulas).
Ed25519 targets the 128-bit security level.
Why Not Use Ed25519?
There is one minor pitfall of Ed25519 that makes it unsuitable for esoteric uses (say, Ring Signature Schemes or zero-knowledge proofs): Ed25519 is not a prime-order group; it has a cofactor h = 8. This detail famously created a double-spend vulnerability in all CryptoNote-based cryptocurrencies (including Monero).
For systems that want the security of Ed25519 and its various well-studied implementations, but still need a prime-order group for their protocol, cryptographers have developed the Ristretto Group to meet your needs.
If you’re working on embedded systems, the determinism inherent to EdDSA might be undesirable due to the possibility of fault attacks. You can use a hedged variant of Ed25519 to mitigate this risk.
Additionally, Ed25519 is not approved for many government applications, although it did make the latest draft revision of FIPS 186 in 2019. If you care about compliance (see above), you cannot use Ed25519. Yet.

Guidance for Ed25519
Unless legally prohibited, Ed25519 should be your default choice, unless you need a prime-order group. In that case, build your desired protocol atop Ristretto255.
If you’re not sure if you need a prime-order group, you probably don’t. It’s a specialized requirement for uncommon use cases (ring signatures, password authenticated key exchange protocols, zero-knowledge proofs, etc.).

The Bitcoin Curve (ECDSA, secp256k1)
Secp256k1 is a Koblitz curve, which is a special case of Weierstrass curves that are more performant when used in binary fields, of the form, 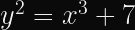
There is no specified reason why Bitcoin chose secp256k1 over another elliptic curve at the time of its inception, but we can speculate:
The author was a pseudonymous contributor to the Metzdowd mailing list for cypherpunks, and probably didn’t trust the NIST curves. Since Ed25519 didn’t exist at the time, the only obvious choice for a hipster elliptic curve parameter selection was to rely on the SECG recommendations, which specify the NIST and Koblitz curves. If you cross the NIST curves off the list, only the Koblitz curves remained.
Therefore, the selection of secp256k1 is likely an artefact of computer history and not a compelling reason to select secp256k1 in new designs. Please look elsewhere.

Secp256k1 targets the 128-bit security level.
Guidance for secp256k1
Don’t bother, there are better options. (i.e. Ed25519)
If you’re writing software for a cryptocurrency-related project, and you feel compelled to use secp256k1 for the sake of reducing your code footprint, please strongly consider the option of burning everything to the proverbial ground.

Art: Swizz
Cryptocurrency Aside, Why Avoid Secp256k1?
As we noted above, secp256k1 isn’t widely used outside of cryptocurrency.
As a direct consequence of this (as we’ll discuss in the NIST P-256 section), most cryptography libraries don’t offer optimized, side-channel-resistant implementations of secp256k1; even if they do offer optimized implementations of NIST P-256.
(Meanwhile, Ed25519 is designed to be side-channel and misuse-resistant, partly due to its Schnorr construction and constant-time ladder for scalar multiplication, so any library that implements Ed25519 is overwhelmingly likely to be constant-time.)
Therefore, any secp256k1 library for most programming languages that isn’t an FFI wrapper for libsecp256k1 will have worse performance than the other 256-bit curves.
https://twitter.com/bascule/status/1320183684935290882
Additionally, secp256k1 implementations are often a source of exploitable side-channels that permit attackers to pilfer your secret keys.
The previously linked article was about BouncyCastle’s implementation (which covers Java and .NET), but there’s still plenty of secp256k1 implementations that don’t FFI libsecp256k1.
From a quick Google Search:
- Python (uses EEA rather than Binary GCD for modular inverse)
- Go (uses Numbers, which weren’t designed for cryptography)
- PHP (uses GMP, which isn’t constant-time)
- JavaScript (calls here, which uses bn.js, which isn’t constant-time)
If you’re using secp256k1, and you’re not basing your choice on cybercash-interop, you’re playing with fire at the implementation and ecosystem levels–even if there are no security problems with the Koblitz curve itself.
You are much better off choosing any different curve than secp256k1 if you don’t have a Bitcoin/Ethereum/etc. interoperability requirement.

Art: LvJ
NIST P-256 (ECDSA, secp256r1)
NIST P-256 is the go-to curve to use with ECDSA in the modern era. Unlike Ed25519, P-256 uses a prime-order group, and is an approved algorithm to use in FIPS-validated modules.
Most cryptography libraries offer optimized assembly implementations of NIST P-256, which makes it less likely that your signing operations will leak timing information or become a significant performance bottleneck.
P-256 targets the 128-bit security level.
Why Not Use P-256?
Once upon a time, P-256 was riskier than Ed25519 (for signatures) and X25519 (for Diffie-Hellman), due to the incomplete addition formulas that led to timing-leaky implementations.
If you’re running old software, you may still be vulnerable to timing attacks that can recover your ECDSA secret key. However, there is a good chance that you’re on a modern and secure implementation in 2022, especially if you’re outsourcing this to OpenSSL or its derivatives.
ECDSA requires a secure randomness source to sign data. If you don’t have one available, and you sign anything, you’re coughing up your secret key to any attacker capable of observing multiple signatures.
Guidance for P-256
P-256 is an acceptable choice, especially if you’re forced to cope with FIPS and/or the CNSA suite requirements when using cryptography.
Of course, if you can get away with Ed25519, use Ed25519 instead.
If you use P-256, make sure you’re using it with SHA-256. Some implementations may default to something weaker (e.g. SHA-1).
If you’re also going to be performing ECDH with P-256, make sure you use compressed points. There used to be a patent; it died in 2018.
If you can afford it, make sure you use deterministic ECDSA (RFC 6979) or hedged signatures (if fault attacks are relevant to your threat model).

NIST P-384 (ECDSA, secp384r1)
NIST P-384 has a larger field than the curves we’ve previously examined, which allows P-384 to target the 192-bit security level. That’s the primary reason why anyone would choose P-384.
Naturally, elliptic curve security is more complicated than merely security against the Elliptic Curve Discrete Logarithm Problem (ECDLP).
P-384 is most often paired with SHA-384, which is the most widely used flavor of the SHA-2 family hash functions that isn’t susceptible to length-extension attacks. (There are also truncated SHA-512 variants specified later, but that’s also what SHA-384 is under-the-hood.)
If you’re aiming to build a “secure-by-default” tool for a system that the US government might one day become a customer of, with minimal cryptographic primitive choice, using NIST P-384 with SHA-384 makes for a reasonably minimalistic bundle.
Why Not Use P-384?
Unlike P-256, most P-384 implementations don’t use constant-time, optimized, and/or formally verified assembly code. (Notable counter-examples: AWS-LC and Go x/crypto.)
Like P-256, P-384 also requires a secure randomness source to sign data. If you aren’t providing one, expect your signing key to end up on fail0verflow one day.
Guidance for P-384
If you use P-384, make sure you’re using it with SHA-384.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

NIST P-521 (ECDSA, secp521r1)
Biggest curve is best curve! — the clueless
https://www.youtube.com/watch?v=i_APoSfCYwU
Systems that choose P-521 often have an interesting threat model, even though said threat model is rarely formally specified.
It’s overwhelmingly likely that what eventually breaks the 256-bit elliptic curves will also break P-521 in short order: Cryptography Relevant Quantum Computers.
The only thing P-521 does against CRQCs that P-256 doesn’t is require more quantum memory. If you’re worried about QRQCs, you might want to look into hybrid post-quantum signature schemes.
If you’re choosing P-521 in your designs, you’re basically saying, “I want to have 256 bits of asymmetric cryptographic security, come hell or high water!” even though the 128-bit security level is likely just fine for your actual threats.
Aside: P-521 and 512-bit ECC Security
P-521 is not a typo, although people sometimes think it is. P-521 uses the Mersenne prime 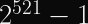
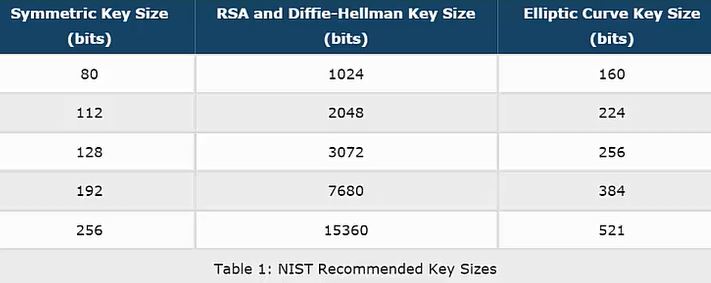
This has led to an unfortunate trend in cryptography media to map ECC key sizes to symmetric security levels that misleads people as to the relationship between the two. For example:
Regrettably, this is misleading, because plotting the ECC Key Size versus equivalent Symmetric Security isn’t a how ECDLP security works. The ratio of the exponents involved is totally linear; it doesn’t suddenly increase beyond 384-bit curves for a mysterious mathematical reason.
- 256-bit Curves target the 128-bit security level
- 384-bit Curves target the 192-bit security level
- 512-bit Curves target the 256-bit security level
- 521-bit Curves actually target the 260-bit security level, but that meets or exceeds the 256-bit security level, so that’s how the standards are interpreted
The reason for this boils down entirely to the best attack against the Elliptic Curve Discrete Logarithm Problem: Pollard’s Rho, which recovers the secret key from an 
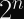
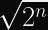
Taking the square root of a number is the same as halving its exponent, so the security level is half: 
Takeaway: If someone tells you that you need a 521-bit curve to meet the 256-bit security level, they are mistaken and it’s not their fault.

Why Not Use P-521?
It’s slow. Much slower than P-256 and Ed25519. Modestly slower than P-384.
Unlike P-384, you’re less likely to find an optimized, constant-time P-521 implementation.
Guidance for P-521
First, make a concerted effort to figure out the motivation for P-521 in your designs. Chances are, someone is putting too much emphasis on the wrong things for security.
If you use P-521, make sure you’re using it with SHA-512.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

Ed448 (EdDSA, Curve448)
Ed448 is the P-521 of the Edwards curves: It mostly exists to give standards committees a psychological comfort for the unlikely event that 256-bit ECC is desperately broken but ECC larger than 384 bits is somehow still safe.
https://twitter.com/dchest/status/703017144053833728
The very concept of having multiple “security levels” for raw cryptography primitives is mostly an artefact of the historical military roots of cryptography, rather than a serious consideration in the modern world.
Unfortunately, this leads to implementations that prioritize runtime algorithm selection negotiation, which maximizes the risk of protocol-level vulnerabilities. See also: JWT.
Ed448 was specified to use SHAKE256, which is a needlessly conservative decision which leads to an unnecessary performance bottleneck.
Why Not Use Ed448?
Aside from the performance hit mentioned previously, there’s no compelling reason to avoid Ed448 that isn’t also true of either Ed25519 or P-384.
Guidance for Ed448
If you want more speed, go with Ed25519. In addition to being faster, Ed25519 is also very widely supported.
If you need a prime-order field, use Decaf with Ed448 or consider P-384.
The Brainpool Curves
The main motivation for the Brainpool curves is that the NIST curves were not generated in a “verifiable pseudo-random way”.
The only reasons you’d ever want to support the Brainpool curves include:
- You think the NIST curves are somehow backdoored by the NSA
- You don’t appreciate small attack surfaces in cryptography libraries
- The German government told you to (see: compliance)
Most of the advice for the NIST Curves at each security level can be copy/pasted for the Brainpool curves, with one important caveat:
When considering real-world implementations, Brainpool curves are more likely to use the general purpose Big Number procedures (which aren’t always constant-time), rather than optimized assembly code, than the NIST curves are.
Therefore, my general guidance for the Brainpool curves is simply:
- Proceed at your own peril
- Consider hiring a cryptography engineer to study the implementation you’re relying on, especially with regard to timing attacks

Art: LvJ
Re-Examining the SafeCurves Criteria
Here’s a 2022 refresh of the SafeCurves criteria for all of the curves considered by this blog post.
| SafeCurve Criteria | Relevance to the Curves Listed Above |
|---|---|
| Fields | All relevant curves satisfy the requirements |
| Equations | All relevant curves satisfy the requirements |
| Base Points | All relevant curves satisfy the requirements |
| Rho | All relevant curves satisfy the requirements |
| Transfers | All relevant curves satisfy the requirements |
| Discriminants | Only secp256k1 doesn’t satisfy the requirements (out of the curves listed in this blog post) |
| Rigidity | The NIST curves do not meet this requirement. If you care about whether or not the standards were manipulated to insert a backdoor, rigidity matters to you. Otherwise, it’s not a deal-breaker. |
| Ladders | While a Montgomery ladder is beneficial for speed and implementation security, it isn’t strictly speaking required. This is an icing-on-the-cake consideration. |
| Twists | The only curve listed above that doesn’t meet the requirement is the 256-bit Brainpool curve (brainpoolp256t1). |
| Completeness | All relevant curves satisfy the requirements, as of 2015. SafeCurves is out of date here. |
| Indistinguishability | All relevant curves satisfy the requirements, as of 2014. |
SafeCurves continues to be a useful resource, especially if you stray from the guidance on this page.
For example: You wouldn’t want to use pairing-friendly curves for general purpose ECC digital signatures, because they’re suitable for specialized problems. SafeCurves correctly recommends not using BN(2,254).
However, SafeCurves is showing its age in 2022. BN curves still end up in digital signature protocol standards even though BLS-12-381 is clearly a better choice.
The Internet would benefit greatly for an updated SafeCurves that focuses on newer elliptic curve algorithms.

TL;DR
Ed25519 is great. NIST P-256 and P-384 are okay (with caveats). Anything else is questionable, and their parameter selection should come with a clear justification.
https://soatok.blog/2022/05/19/guidance-for-choosing-an-elliptic-curve-signature-algorithm-in-2022/
#asymmetricCryptography #BrainpoolCurves #cryptography #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #ellipticCurveCryptography #P256 #P384 #P521 #secp256k1 #secp256r1 #secp384r1 #secp521r1 #SecurityGuidance
A question I get asked frequently is, “How did you learn cryptography?”I could certainly tell everyone my history as a self-taught programmer who discovered cryptography when, after my website for my indie game projects kept getting hacked, I was introduced to cryptographic hash functions… but I suspect the question folks want answered is, “How would you recommend I learn cryptography?” rather than my cautionary tale about poorly-implemented password hash being a gateway bug.
The Traditional Ways to Learn
There are two traditional ways to learn cryptography.If you want a book to augment your journey in either traditional path, I recommend Serious Cryptography by Jean-Philippe Aumasson.
Academic Cryptography
The traditional academic way to learn cryptography involves a lot of self-study about number theory, linear algebra, discrete mathematics, probability, permutations, and field theory.You’d typically start off with classical ciphers (Caesar, etc.) then work your way through the history of ciphers until you finally reach an introduction to the math underpinning RSA and Diffie-Hellman, and maybe taught about Schneier’s Law and cautioned to only use AES and SHA-2… and then you’re left to your own devices unless you pursue a degree in cryptography.
The end result of people carelessly exploring this path is a lot of designs like Telegram’s MTProto that do stupid things with exotic block cipher modes and misusing vanilla cryptographic hash functions as message authentication codes; often with textbook a.k.a. unpadded RSA, AES in ECB, CBC, or some rarely-used mode that the author had to write custom code to handle (using ECB mode under the hood), and (until recently) SHA-1.
People who decide to pursue cryptography as a serious academic discipline will not make these mistakes. They’re far too apt for the common mistakes. Instead, they run the risk of spending years involved in esoteric research about homomorphic encryption, cryptographic pairings, and other cool stuff that might not see real world deployment (outside of novel cryptocurrency hobby projects) for five or more years.
That is to say: Academia is a valid path to pursue, but it’s not for everyone.
If you want to explore this path, Cryptography I by Dan Boneh is a great starting point.
Security Industry-Driven Cryptography
The other traditional way to learn cryptography is to break existing cryptography implementations. This isn’t always as difficult as it may sound: Reverse engineering video games to defeat anti-cheat protections has led several of my friends into learning about cryptography.For security-minded folks, the best place to start is the CryptoPals challenges. Another alternative is CryptoHack.
There are also plenty of CTF events all year around, but they’re rarely a good cryptography learning exercise above what CryptoPals offers. (Though there are notable exceptions.)
A Practical Approach to Learning Cryptography
Art by Kyume.
If you’re coming from a computer programming background and want to learn cryptography, the traditional approaches carry the risk of Reasoning By Lego.
Instead, the approach I recommend is to start gaining experience with the safest, highest-level libraries and then slowly working your way down into the details.
This approach has two benefits:
- If you have to implement something while you’re still learning, your knowledge and experience is stilted towards “use something safe and secure” not “hack together something with Blowfish in ECB mode and MD5 because they’re familiar”.
- You can let your own curiosity guide your education rather than follow someone else’s study guide.
To illustrate what this looks like, here’s how a JavaScript developer might approach learning cryptography, starting from the most easy-mode library and drilling down into specifics.
Super Easy Mode: DholeCrypto
Disclaimer: This is my project.Dhole Crypto is an open source library, implemented in JavaScript and PHP and powered by libsodium, that tries to make security as easy as possible.
I designed Dhole Crypto for securing my own projects without increasing the cognitive load of anyone reviewing my code.
If you’re an experienced programmer, you should be able to successfully use Dhole Crypto in a Node.js/PHP project. If it does not come easy, that is a bug that should be fixed immediately.
Easy Mode: Libsodium
Using libsodium is slightly more involved than Dhole Crypto: Now you have to know what a nonce is, and take care to manage them carefully.Advantage: Your code will be faster than if you used Dhole Crypto.
Libsodium is still pretty easy. If you use this cheat sheet, you can implement something secure without much effort. If you deviate from the cheat sheet, pay careful attention to the documentation.
If you’re writing system software (i.e. programming in C), libsodium is an incredibly easy-to-use library.
Moderate Difficulty: Implementing Protocols
Let’s say you’re working on a project where libsodium is overkill, and you only need a few cryptography primitives and constructions (e.g. XChaCha20-Poly1305). A good example: In-browser JavaScript.Instead of forcing your users to download the entire Sodium library, you might opt to implement a compatible construction using JavaScript implementations of these primitives.
Since you have trusted implementations to test your construction against, this should be a comparatively low-risk effort (assuming the primitive implementations are also secure), but it’s not one that should be undertaken without all of the prior experience.
Note: At this stage you are not implementing the primitives, just using them.
Hard Difficulty: Designing Protocols and Constructions
Repeat after me: “I will not roll my own crypto before I’m ready.” Art by AtlasInu.
To distinguish: TLS and Noise are protocols. AES-GCM and XChaCha20-Poly1305 are constructions.
Once you’ve implemented protocols and constructions, the next step in your self-education is to design new ones.
Maybe you want to combine XChaCha20 with a MAC based on the BLAKE3 hash function, with some sort of SIV to make the whole shebang nonce-misuse resistant?
You wouldn’t want to dive headfirst into cryptography protocol/construction design without all of the prior experience.
Very Hard Mode: Implementing Cryptographic Primitives
It’s not so much that cryptography primitives are hard to implement. You could fit RC4 in a tweet before they raised the character limit to 280. (Don’t use RC4 though!)The hard part is that they’re hard to implement securely. See also: LadderLeak.
Usually when you get to this stage in your education, you will have also picked up one or both of the traditional paths to augment your understanding. If not, you really should.
Nightmare Mode: Designing Cryptography Primitives
A lot of people like to dive straight into this stage early in their education. This usually ends in tears.If you’ve mastered every step in my prescribed outline and pursued both of the traditional paths to the point that you have a novel published attack in a peer-reviewed journal (and mirrored on ePrint), then you’re probably ready for this stage.
Bonus: If you’re a furry and you become a cryptography expert, you can call yourself a cryptografur. If you had no other reason to learn cryptography, do it just for pun!
Header art by circuitslime.
https://soatok.blog/2020/06/10/how-to-learn-cryptography-as-a-programmer/
#cryptography #education #programming #Technology

Did you know that, in the Furry Fandom, the most popular choice in species for one’s fursona is actually a hybrid?
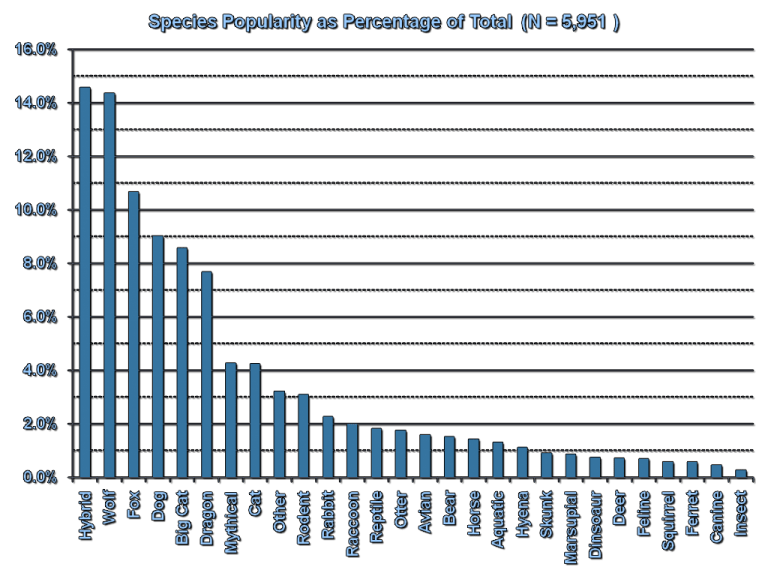
Of course, we’re not talking about that kind of hybrid today. I just thought it was an amusing coincidence.

Nor are we talking about what comes to mind for engineers accustomed to classical cryptography when you say Hybrid.
(Such engineers typically envision some combination of asymmetric key encapsulation with symmetric encryption; because too many people encrypt with RSA directly and the sane approach is often described as a Hybrid Cryptosystem in the literature.)
Rather, Hybrid Cryptography in today’s context refers to:
Cryptography systems that use a post-quantum cryptography algorithm, combined with one of the algorithms deployed today that aren’t resistant to quantum computers.
If you need to differentiate the two, PQ-Hybrid might be a better designation.
Why Hybrid Cryptosystems?
At some point in the future (years or decades from now), humanity may build a practical quantum computer. This will be a complete disaster for all of the cryptography deployed on the Internet today.
In response to this distant existential threat, cryptographers have been hard at work designing and attacking algorithms that remain secure even when quantum computers arrive. These algorithms are classified as post-quantum cryptography (mostly to distinguish it from techniques that uses quantum computers to facilitate cryptography rather than attack it, which is “quantum cryptography” and not really worth our time talking about). Post-quantum cryptography is often abbreviated as “PQ Crypto” or “PQC”.
However, a lot of the post-quantum cryptography designs are relatively new or comparatively less studied than their classical (pre-quantum) counterparts. Several of the Round 1 candidates to NIST’s post quantum cryptography project were broken immediately (PDF). Exploit code referenced in PDF duplicated below.:
#!/usr/bin/env python3import binascii, structdef recover_bit(ct, bit): assert bit < len(ct) // 4000 ts = [struct.unpack('BB', ct[i:i+2]) for i in range(4000*bit, 4000*(bit+1), 2)] xs, ys = [a for a, b in ts if b == 1], [a for a, b in ts if b == 2] return sum(xs) / len(xs) >= sum(ys) / len(ys)def decrypt(ct): res = sum(recover_bit(ct, b) << b for b in range(len(ct) // 4000)) return int.to_bytes(res, len(ct) // 4000 // 8, 'little')kat = 0for l in open('KAT_GuessAgain/GuessAgainEncryptKAT_2000.rsp'): if l.startswith('msg = '): # only used for verifying the recovered plaintext. msg = binascii.unhexlify(l[len('msg = '):].strip()) elif l.startswith('c = '): ct = binascii.unhexlify(l[len('c = '):].strip()) print('{}attacking known-answer test #{}'.format('\n' * (kat > 0), kat)) print('correct plaintext: {}'.format(binascii.hexlify(msg).decode())) plain = decrypt(ct) print('recovered plaintext: {} ({})'.format(binascii.hexlify(plain).decode(), plain == msg)) kat += 1
More pertinent to our discussions: Rainbow, which was one of the Round 3 Finalists for post-quantum digital signature algorithms, was discovered in 2020 to be much easier to attack than previously thought. Specifically, for the third round parameters, the attack cost was reduced by a factor of 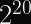
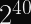

That security reduction is just a tad bit more concerning than a Round 1 candidate being totally broken, since NIST had concluded by then that Rainbow was a good signature algorithm until that attack was discovered. Maybe there are similar attacks just waiting to be found?
Given that new cryptography is accompanied by less confidence than incumbent cryptography, hybrid designs are an excellent way to mitigate the risk of attack advancements in post-quantum cryptography:
If the security of your system requires breaking the cryptography used today AND breaking one of the new-fangled designs, you’ll always be at least as secure as the stronger algorithm.

Why Is Hybrid Cryptography Controversial?
Despite the risks of greenfield cryptographic algorithms, the NSA has begun recommending a strictly-PQ approach to cryptography and have explicitly stated that they will not require hybrid designs.
Another pushback on hybrid cryptography comes from Uri Blumenthal of MIT’s Lincoln Labs on the IETF CFRG mailing list (the acronym CRQC expands to “Cryptographically-Relevant Quantum Computer”):
Here are the possibilities and their relation to the usefulness of the Hybrid approach.1. CRQC arrived, Classic hold against classic attacks, PQ algorithms hold – Hybrid is useless.
2. CRQC arrived, Classic hold against classic attacks, PQ algorithms fail – Hybrid is useless.
3. CRQC arrived, Classic broken against classic attacks, PQ algorithms hold – Hybrid is useless.
4. CRQC arrived, Classic hold against classic attacks, PQ algorithms broken – Hybrid useless.
5. CRQC doesn’t arrive, Classic hold against classic attacks, PQ algorithms hold – Hybrid is useless.
6. CRQC doesn’t arrive, Classic hold against classic attacks, PQ algorithms broken – Hybrid helps.
7. CRQC doesn’t arrive, Classic broken against classic attacks, PQ algorithms hold – Hybrid is useless.
8. CRQC doesn’t arrive, Classic broken against classic attacks, PQ algorithms broken – Hybrid is useless.
Uri Blumenthal, IETF CFRG mailing list, December 2021 (link)
Why Hybrid Is Actually A Damn Good Idea

Uri’s risk analysis is, of course, flawed. And I’m not the first to disagree with him.
First, Uri’s framing sort of implies that each of the 8 possible outputs of these 3 boolean variables are relatively equally likely outcomes.
It’s very tempting to look at this and think, “Wow, that’s a lot of work for something that only helps in 12.5% of possible outcomes!” Uri didn’t explicitly state this assumption, and he might not even believe that, but it is a cognitive trap that emerges in the structure of his argument, so watch your step.
Second, for many candidate algorithms, we’re already in scenario 6 that Uri outlined! It’s not some hypothetical future, it’s the present state of affairs.
To wit: The advances in cryptanalysis on Rainbow don’t totally break it in a practical sense, but they do reduce the security by a devastating margin (which will require significantly larger parameter sets and performance penalties to remedy).
For many post-quantum algorithms, we’re still uncertain about which scenario is most relevant. But since PQ algorithms are being successfully attacked and a quantum computer still hasn’t arrived, and classical algorithms are still holding up fine, it’s very clear that “hybrid helps” is the world we most likely inhabit today, and likely will for many years (until the existence of quantum computers is finally settled).
Finally, even in other scenarios (which are more relevant for other post-quantum algorithms), hybrid doesn’t significantly hurt security. It does carry a minor cost to bandwidth and performance, and it does mean having a larger codebase to review when compared with jettisoning the algorithms we use today, but I’d argue that the existing code is relatively low risk compared to new code.
From what I’ve read, the NSA didn’t make as strong an argument as Uri; they said hybrid would not be required, but didn’t go so far as to attack it.
Hybrid cryptography is a long-term bet that will protect the most users from cryptanalytic advancements, contrasted with strictly-PQ and no-PQ approaches.
Why The Hybrid Controversy Remains Unsettled
Even if we can all agree that hybrid is the way to go, there’s still significant disagreement on exactly how to do it.
Hybrid KEMs
There are two schools of thought on hybrid Key Encapsulation Mechanisms (KEMs):
- Wrap the post-quantum KEM in the encrypted channel created by the classical KEM.
- Use both the post-quantum KEM and classical KEM as inputs to a secure KDF, then use a single encrypted channel secured by both.
The first option (layered) has the benefit of making migrations smoother. You can begin with classical cryptography (i.e. ECDHE for TLS ciphersuites), which is what most systems online support today. Then you can do your post-quantum cryptography inside the existing channel to create a post-quantum-secure channel. This also lends toward opportunistic upgrades (which might not be a good idea).
The second option (composite) has the benefit of making the security of your protocol all-or-nothing: You cannot attack the weak now and the strong part later. The session keys you’ll derive require attacking both algorithms in order to get access to the plaintext. Additionally, you only need a single layer. The complexity lies entirely within the handshake, instead of every packet.
Personally, I think composite is a better option for security than layered.
Hybrid Signatures
There are, additionally, two different schools of thought on hybrid digital signature algorithms. However, the difference is more subtle than with KEMs.
- Require separate classical signatures and post-quantum signatures.
- Specify a composite mode that combines the two together and treat it as a distinct algorithm.
To better illustrate what this looks like, I outlined what a composite hybrid digital signature algorithm could look like on the CFRG mailing list:
primary_seed := randombytes_buf(64) // store thised25519_seed := hash_sha512256(PREFIX_CLASSICAL || primary_seed)pq_seed := hash_sha512256(PREFIX_POSTQUANTUM || primary_seed)ed25519_keypair := crypto_sign_seed_keypair(ed25519_seed)pq_keypair := pqcrypto_sign_seed_keypair(pq_seed)
Your composite public key would be your Ed25519 public key, followed by your post-quantum public key. Since Ed25519 public keys are always 32 bytes, this is easy to implement securely.
Every composite signature would be an Ed25519 signature concatenated with the post-quantum signature. Since Ed25519 signatures are always 64 bytes, this leads to a predictable signature size relative to the post-quantum signature.
The main motivation for preferring a composite hybrid signature over a detached hybrid signature is to push the hybridization of cryptography lower in the stack so developers don’t have to think about these details. They just select HYBRIDSIG1 or HYBRIDSIG2 in their ciphersuite configuration, and cryptographers get to decide what that means.
TL;DR
Hybrid designs of post-quantum crypto are good, and I think composite hybrid designs make the most sense for both KEMs and signatures.
https://soatok.blog/2022/01/27/the-controversy-surrounding-hybrid-cryptography/
#asymmetricCryptography #classicalCryptography #cryptography #digitalSignatureAlgorithm #hybridCryptography #hybridDesigns #KEM #keyEncapsulationMechanism #NISTPostQuantumCryptographyProject #NISTPQC #postQuantumCryptography
Let me state up front that, while we’re going to be talking about an open source project that was recently submitted to Hacker News’s “Show HN” section, the intent of this post is not at all to shame the developer who tried their damnedest to do the right thing. They’re the victim, not the culprit.RSA, Ya Don’t Say
Earlier this week, an HN user shared their open source fork of a Facebook’s messenger client, with added encryption. Their motivation was, as stated in the readme:It is known that Facebook scans your messages. If you need to keep using Facebook messenger but care about privacy, Zuccnet might help.It’s pretty simple: you and your friend have Zuccnet installed. Your friend gives you their Zuccnet public key. Then, when you send a message to your friend on Zuccnet, your message is encrypted on your machine before it is sent across Facebook to your friend. Then, your friend’s Zuccnet decrypts the message. Facebook never sees the content of your message.
I’m not a security person and there’s probably some stuff I’ve missed – any contributions are very welcome! This is very beta, don’t take it too seriously.
From Zuccnet’s very humble README.
So far, so good. Facebook is abysmal for privacy, so trying to take matters into your own hands to encrypt data so Facebook can’t see what you’re talking about is, in spirit, a wonderful idea.
(Art by Khia.)
However, there is a problem with the execution of this idea. And this isn’t a problem unique to Zuccnet. Several times per year, I come across some well-meaning software project that makes the same mistake: Encrypting messages with RSA directly is bad.
From the Zuccnet source code:
const encryptMessage = (message, recipientPublicKey) => { const encryptedMessage = crypto.publicEncrypt( { key: recipientPublicKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(message), ); return encryptedMessage.toString("base64");};/** * * @param {String} encryptedMessage - base64 encoded string */const decryptMessage = encryptedMessage => { const encryptedMessageBuffer = Buffer.from(encryptedMessage, "base64"); const { privateKey } = getOrCreateZuccnetKeyPair(); const message = crypto.privateDecrypt( { key: privateKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(encryptedMessageBuffer), );};
To the Zuccnet author’s credit, they’re using OAEP padding, not PKCS#1 v1.5 padding. This means their code isn’t vulnerable to Bleichenbacher’s 1998 padding oracle attack (n.b. most of the RSA code I encounter in the wild is vulnerable to this attack).
However, there are other problems with this code:
- If you try to encrypt a message longer than 256 bytes with a 2048-bit RSA public key, it will fail. (Bytes matter here, not characters, even for English speakers–because emoji.)
- This design (encrypting with a static RSA public key per recipient) completely lacks forward secrecy. This is the same reason that PGP encryption sucks (or, at least, one of the reasons PGP sucks).
There are many ways to work around the first limitation.
Some cryptography libraries let you treat RSA as a block cipher in ECB mode and encrypt each chunk independently. This is an incredibly stupid API deign choice: It’s slow (asymmetric cryptography operations are on the order of tens-to-hundreds-of-thousands times slower than symmetric cryptography) and you can drop/reorder/replay blocks, since ECB mode provides no semantic security.
I have strong opinions about cryptographic library design.
(Art by Swizz.)A much better strategy is to encrypt the data with a symmetric key, then encrypt that key with RSA. (See the end of the post for special treatment options that are especially helpful for RSA with PKCS#1 v1.5 padding.)
Working around the second problem usually requires an Authenticated Key Exchange (AKE), similar to what I covered in my Guide to End-to-End Encryption. Working around this second problem also solves the first problem, so it’s usually better to just implement a forward-secret key exchange protocol than try to make RSA secure.
(You can get forward secrecy without an AKE, by regularly rotating keys, but AKEs make forward secrecy automatic and on-by-default without forcing humans to make a decision to rotate a credential– something most people don’t do unless they have to. AKEs trade user experience complexity for protocol complexity–and this trade-off is almost universally worth taking.)
Although AKEs are extremely useful, they’re a bit complex for most software developers to pick up without prior cryptography experience. (If they were easier, after all, there wouldn’t be so much software that encrypts messages directly with RSA in the first place.)
Note: RSA itself isn’t the reason that this lacks forward secrecy. The problem is how RSA is used.
Recommendations
For Developers
First, consider not using RSA. Hell, while you’re at it, don’t write any cryptography code that you don’t have to.Libsodium (which you should use) does most of this for you, and can easily be turned into an AKE comparable to the one Signal uses. The less cryptography code you have to write, the less can go catastrophically wrong–especially in production systems.
If jettisoning RSA from your designs is a non-starter, you should at least consider taking the Dhole Moments Pledge for Software Developers:
I will not encrypt messages directly with RSA, or any other asymmetric primitive.Simple enough, right?
Instead, if you find yourself needing to encrypt a message with RSA, remind yourself that RSA is for encrypting symmetric keys, not messages. And then plan your protocol design accordingly.Also, I’m pretty sure RSA isn’t random-key robust. Ask your favorite cryptographer if it matters for whatever you’re building.
(But seriously, you’re better off not using RSA at all.)
For Cryptography Libraries
Let’s ask ourselves, “Why are we forcing developers to know or even care about these details?”Libsodium doesn’t encumber developers with unnecessary decisions like this. Why does the crypto module built into JavaScript? Why does the crypto module built into most programming languages that offer one, for that matter? (Go is a notable exception here, because their security team is awesome and forward-thinking.)
In my opinion, we should stop shipping cryptography interfaces that…
- Mix symmetric and asymmetric cryptography in the same API
- Allow developers to encrypt directly with asymmetric primitives
- Force developers to manage their own nonces/initialization vectors
- Allow public/private keys to easily get confused (e.g. lack of type safety)
For example: Dhole Crypto is close to my ideal for general-purpose encryption.
Addendum: Securing RSA with PKCS#1 v1.5
Update: Neil Madden informs me that what I wrote here is actually very similar to a standard construction called RSA-KEM. You should use RSA-KEM instead of what I’ve sketched out, since that’s better studied by cryptographers.(I’ve removed the original sketch below, to prevent accidental misuse.)
https://soatok.blog/2021/01/20/please-stop-encrypting-with-rsa-directly/
#asymmetricCryptography #cryptography #RSA #SecurityGuidance #symmetricCryptography

In 2017, cryptography researchers from Kudelski Security demonstrated practical fault attacks against EdDSA (specifically Ed25519; RFC 8032).
Their techniques are also applicable to Deterministic ECDSA (RFC 6979), and potentially work against any deterministic signature scheme (n.b. the Fiat-Shamir or Schnorr distinction isn’t meaningful in this context).

Although that might seem alarming, fault attacks aren’t especially useful for software applications running on general-purpose computers. They’re mostly in the threat models for smartcards and embedded devices.
A recent paper discusses a technique called “hedged” signatures, which I’ve mentioned in A Furry’s Guide to Digital Signature Algorithms.
What is a Hedged Signature?
Let’s just consult the formal definition given by Aranha, et al. in the paper I linked above!
Okay, if you’re not a cryptographer, this is probably clear as mud.
Let’s try a different approach (one that most software engineers will find more intuitive). We’ll start with non-hedged signatures, and then tweak them to become hedged.
Libsodium: Non-Hedged Signatures
Libsodium’s crypto_sign_detached() (which implements Ed25519) accepts two arguments:
- The message being signed.
- The secret key held by the signer.
Libsodium’s congruents crypto_sign_verify_detached() accepts three arguments:
- The detached signature.
- The message.
- The public key (corresponds to the secret key from the other function).
Since libsodium uses Ed25519 under-the-hood, the signature algorithm is deterministic: If you sign the same message with the same secret key, it will always produce the same signature.
Don’t believe me? Try it yourself: https://3v4l.org/lKrJb
Dhole Crypto: Hedged Signatures
Last year when I wrote Dhole Cryptography (in PHP and JavaScript), I decided to implement what would later come to be called “hedged signatures” by cryptographers.
Instead of just signing a message, Dhole Crypto first generates a 256-bit per-message nonce and then signs the nonce and the message together. Then, it appends the nonce to the generated signature (and encodes this as one binary-safe string).
That is to say, the major hack is to change a procedure from this:
function sign(string $message, string $secretKey): string { $signature = sodium_crypto_sign_detached( $message, $secretKey ); return base64_encode($signature);}
…into a procedure that looks like this:
function hsign(string $message, string $secretKey): string { $nonce = random_bytes(32); $signature = sodium_crypto_sign_detached( $nonce . $message, $secretKey ); return base64_encode($signature . $nonce);}
If you pay careful attention to the placement of the nonce in this updated procedure, you’ll notice that it’s backwards compatible with the original libsodium API for Ed25519: crypto_sign() and crypto_sign_open().
Of course, these details are totally abstracted away from the user. Instead, the API looks like this (PHP):
<?phpuse Soatok\DholeCrypto\Asymmetric;use Soatok\DholeCrypto\Key\AsymmetricSecretKey;// Key generation$secret = AsymmetricSecretKey::generate();$public = $secret->getPublicKey();// Signing a message$message = "I certify that you have paid your $350 awoo fine";$sig = Asymmetric::sign($message, $secret);// Verifying a message and signatureif (!Asymmetric::verify($message, $public, $sig)) { die('AWOO FINE UNPAID');}
For JavaScript developers, this may be more intuitive to read:
const { Asymmetric, AsymmetricSecretKey} = require('dhole-crypto');(async function () { let wolfSecret = await AsymmetricSecretKey.generate(); let wolfPublic = wolfSecret.getPublicKey(); let message = "Your $350 awoo fine has been paid UwU"; let signature = await Asymmetric.sign(message, wolfSecret); if (!await Asymmetric.verify(message, wolfPublic, signature)) { console.log("Invalid signature. Awoo not authorized."); }})();
Do Hedged Signatures Protect Against Fault Attacks?
Sort of. It really depends on the kind of fault attack the attacker uses.
See Section 5 of the paper for a detailed break-down of the provable security of hedged signatures against XEdDSA (a variant of EdDSA used by the Signal protocol; the EdDSA variants specified in RFC 8032 were not studied in that paper).
However, the exploit explored by Kudelski using simple voltage glitches to break EdDSA in an Arduino device does become significantly more difficult with hedged signatures versus classical EdDSA.
Additionally, if you combine the existing techniques for mitigating fault attacks in embedded software with a protocol that uses hedged signatures, you may push the cost of a successful fault attack to become economically impractical for attackers.
However, it’s demonstrable that Hedged Signatures are at least as secure as Deterministic Signatures:
Even if your hedging suffers from a catastrophic randomness failure and generates the same nonce twice, the actual nonce used within Ed25519 will be derived from the SHA-512 hash of this value, the message, and a secret key.
Consequently, the only way for the internal nonce to repeat is for the message to be the same–which is the same scenario as a Deterministic Signature, which doesn’t let attackers steal your secret key.

What Does This All Mean?
Hedged signatures are at least as safe as Deterministic Signatures, and in some scenarios, offer a greater degree of protection than Deterministic Signatures.
Additionally, it’s very easy to convert a Deterministic Signature scheme into a Hedged Signature Scheme: Just add additional randomness that gets signed as part of the message, then append this randomness to the signature (so the signature can be successfully verified later).
Or, if you’re using a programming language that I publish open source software in, you can just use Dhole Cryptography and not worry about these details.
(Header art by Kyume.)
https://soatok.blog/2020/05/03/hedged-signatures-with-libsodium-using-dhole/
#crypto #cryptography #DholeCryptography #digitalSignatureAlgorithm #Ed25519 #EdDSA #hedgedSignatures #JavaScript #libsodium #openSource #PHP
Let’s talk about digital signature algorithms.Digital signature algorithms are one of the coolest ideas to come out of asymmetric (a.k.a. public-key) cryptography, but they’re so simple and straightforward that most cryptography nerds don’t spend a lot of time thinking about them.
Even though you are more likely to run into a digital signature as a building block (e.g. certificate signatures in TLS) than think about them in isolation (e.g. secure software releases), they’re still really cool and worth learning about.
What’s a Digital Signature?
A digital signature is some string that proves that a specific message was signed by some specific entity in possession of the secret half of an asymmetric key-pair. Digital Signature Algorithms define the process for securely signing and verifying messages with their associated signatures.For example, if I have the following keypair:
- Secret key:
9080a2c7897faeb8526968161695da0f7b3afa2e8e7d8e8369a85547ab48ea05- Public key:
482b8d3430445cdad6b5ce59778e09ab59d099120f32d316e881db1a6330390bI can cryptographically sign the message “Dhole Moments: Never a dull moment!” with the above secret key, and it will generate the signature string:
63629779a31b623486145359c6f1d56602d8d9135e4b17fa2ae3667c8947397decd7ae01bfed08645a429f5dee906e87df4e18eefdfff9acb5b1488c9dec800f.If you only have the message, signature string, and my public key, you can verify that I signed the message. But, very crucially, you cannot sign messages and convince someone else that they came from me. (With symmetric authentication schemes, such as HMAC, you can.)
A digital signature algorithm is considered secure if, in order for anyone else to pass off a different message as being signed by me, they would need my secret key to succeed. When this assumption holds true, we say the scheme is secure against existential forgery attacks.
How Do Digital Signatures Work?
Simple answer: They generally combine a cryptographic hash function (e.g. SHA-256) with some asymmetric operation, and the details beyond that are all magic.More complicated answer: That depends entirely on the algorithm in question!
Art by Swizz
For example, with RSA signatures, you actually encrypt a hash of the message with your secret key to sign the message, and then you RSA-decrypt it with your public key to verify the signature. This is backwards from RSA encryption (where you do the totally sane thing: encrypt with public key, decrypt with secret key).
In contrast, with ECDSA signatures, you’re doing point arithmetic over an elliptic curve (with a per-signature random value).
Yet another class of digital signature algorithms are hash-based signatures, such as SPHINCS+ from the NIST Post-Quantum Cryptography Standardization effort, wherein your internals consist entirely of hash functions (and trees of hash functions, and stream ciphers built with other hash functions).
In all cases, the fundamental principle stays the same: You sign a message with a secret key, and can verify it with a public key.
In the interest of time, I’m not going to dive deep into how each signature algorithm works. That can be the subject of future blog posts (one for each of the algorithms in question).
Quick aside: Cryptographers who stumble across my blog might notice that I deviate from convention a bit. They typically refer to the sensitive half of an asymmetric key pair as a “private key”, but I instead call it a “secret key”.
The main reason for this is that “secret key” can be abbreviated as “sk” and public key can be abbreviated as “pk”, whereas private/public doesn’t share this convenience. If you ever come across their writings and wonder about this discrepancy, I’m breaking away from the norm and their way is more in line with the orthodoxy.
What Algorithms Should I Use?
What algorithm, indeed! (Art by circuitslime)
If you find yourself asking this question, you’re probably dangerously close to rolling your own crypto. If so, you’ll want to hire a cryptographer to make sure your designs aren’t insecure. (It’s extremely easy to design or implement otherwise-secure cryptography in an insecure way.)
Recommended Digital Signature Algorithms
(Update, 2022-05-19): I’ve published a more in-depth treatment of the Elliptic Curve Digital Signature Algorithms a few years after this post was created. A lot of the topics covered by EdDSA and ECDSA are focused on there.EdDSA: Edwards Curve DSA
EdDSA comes in two variants: Ed25519 (widely supported in a lot of libraries and protocols) and Ed448 (higher security level, but not implemented or supported in as many places).The IETF standardized EdDSA in RFC 8032, in an effort related to the standardization of RFC 7748 (titled: Elliptic Curves for Security).
Formally, EdDSA is derived from Schnorr signatures and defined over Edwards curves. EdDSA’s design was motivated by the real-world security failures of ECDSA:
- Whereas ECDSA requires a per-signature secret number (
) to protect the secret key, EdDSA derives the per-signature nonce deterministically from a hash of the secret key and message.
- ECDSA with biased nonces can also leak your secret key through lattice attacks. To side-step this, EdDSA uses a hash function twice the size as the prime (i.e. SHA-512 for Ed25519), which guarantees that the distribution of the output of the modular reduction is unbiased (assuming uniform random inputs).
- ECDSA implemented over the NIST Curves is difficult to implement in constant-time: Complicated point arithmetic rules, point division, etc. EdDSA only uses operations that are easy to implement in constant-time.
For a real-world example of why EdDSA is better than ECDSA, look no further than the Minerva attacks, and the Ed25519 designer’s notes on why EdDSA stood up to the attacks.
The security benefits of EdDSA over ECDSA are so vast that FIPS 186-5 is going to include Ed25519 and Ed448.
Hooray for EdDSA adoption even in federal hellscapes.
This is kind of a big deal! The FIPS standards are notoriously slow-moving, and they’re deeply committed to a sunk cost fallacy on algorithms they previously deemed acceptable for real-world deployment.
RFC 6979: Deterministic ECDSA
Despite EdDSA being superior to ECDSA in virtually every way (performance, security, misuse-resistance), a lot of systems still require ECDSA support for the foreseeable future.If ECDSA is here to stay, we might as well make it suck less in real-world deployments. And that’s exactly what Thomas Pornin did when he wrote RFC 6979: Deterministic Usage of DSA and ECDSA.
(Like EdDSA, Deterministic ECDSA is on its way to FIPS 186-5. Look for it in FIPS-compliant hardware 5 years from now when people actually bother to update their implementations.)
Acceptable Digital Signature Algorithms
ECDSA Signatures
The Elliptic Curve Digital Signature Algorithm (ECDSA) is the incumbent design for signatures. Unlike EdDSA, ECDSA is a more flexible design that has been applied to many different types of curves.This is more of a curse than a blessing, as Microsoft discovered with CVE-2020-0601: You could take an existing (signature, public key) pair with standard curve, explicitly set the generator point equal to the victim’s public key, and set your secret key to 1, and Windows’s cryptography library would think, “This is fine.”
For this reason, cryptographers were generally wary of proposals to add support for Koblitz curves (including secp256k1–the Bitcoin curve) or Brainpool curves into protocols that are totally fine with NIST P-256 (and maybe NIST P-384 if you need it for compliance reasons).
For that reason, if you can’t use EdDSA or RFC 6979, your fallback option is ECDSA with one of those two curves (secp256r1, secp384r1), and making sure that you have access to a reliable cryptographic random number generator.
RSA Signatures
It’s high time the world stopped using RSA.Not just for the reasons that Trail of Bits is arguing (which I happen to agree with), but more importantly:
Replacing RSA with EdDSA (or Deterministic ECDSA) also gives teams an opportunity to practice migrating from one cryptography algorithm suite to another, which will probably be a much-needed experience when quantum computers come along and we’re all forced to migrate to post-quantum cryptography.
Encryption is a bigger risk of being broken by quantum computers than signature schemes: If you encrypt data today, a quantum computer 20 years down the line can decrypt it immediately. Conversely, messages that are signed today cannot be broken until after a quantum computer exists.
That being said, if you only need signatures and not encryption, RSA is still acceptable. If you also need encryption, don’t use RSA for that purpose.
If you can, use PSS padding rather than PKCS#1 v1.5 padding, with SHA-256 or SHA-384. But for signatures (i.e. not encryption), PKCS#1 v1.5 padding is fine.
Dishonorable Mention
DSA Signatures
There’s really no point in using classical DSA, when ECDSA is widely supported and has more ongoing attention from cryptography experts.If you’re designing a system in 2020 that uses DSA, my only question for you is…
WHYYYYYY?! (Art by Khia)
Upcoming Signature Algorithms
Although it is far too early to consider adopting these yet, cryptographers are working on new designs that protect against wider ranges of real-world threats.Let’s briefly look at some of them and speculate wildly about what the future looks like. For fun. Don’t use these yet, unless you have a very good reason to do so.
Digital Signature Research Topics
Hedged Signatures
Above, we concluded that EdDSA and Deterministic ECDSA were generally the best choice (and what I’d recommend for software developers). There is one important caveat: Fault attacks.A fault attack is when you induce a hardware fault into a computer chip, and thereby interfere with the correct functioning of a cryptography algorithm. This is especially relevant to embedded devices and IoT.
The IETF’s CFRG is investigating the use of additional randomization of messages (rather than randomizing signatures) as a safeguard against leaking secret keys through fault injection.
Of course, the Dhole Cryptography Library (my libsodium wrapper for JavaScript and PHP) already provides a form of Hedged Signatures.
If this technique is proven successful at mitigating fault injection attacks, then libsodium users will be able to follow the technique outlined in Dhole Crypto to safeguard their own protocols against fault attacks. Until then, they’re at least as safe as deterministic EdDSA today.
Threshold ECDSA Signatures
Suppose you have a scenario where you want 3-or-more people to have to sign a message before it’s valid. That’s exactly what Threshold ECDSA with Fast Trustless Setup aspires to provide.Although this is mostly being implemented in cryptocurrency projects today, the cryptography underpinnings are fascinating. At worst, this will be one good side-effect to come from blockchain mania.
Post-Quantum Digital Signatures
Hash-Based Signatures
The best hash-based signature schemes are based on the SPHINCS design for one simple reason: It’s stateless.In earlier hash-based digital signatures, such as XMSS, you have to maintain a state of which keys you’ve already used, to prevent attacks. Google’s Adam Langley previously described this as a “huge foot-cannon” for security (although probably okay in some environments, such as an HSM).
Lattice-Based Signatures
There are a lot of post-quantum signature algorithm designs defined over lattice groups, but my favorite lattice-based design is called FALCON. FALCON stands for FAst-Fourier Lattice-based COmpact Signatures Over NTRU.Sign Here, Please
Who knew there would be so much complexity involved with such a simple cryptographic operation? And we didn’t even dive deep on how any of them work.
That’s the problem with cryptography: It’s a fractal of complexity. The more you know about these topics, the deeper the complexity becomes.
But if you’re implementing a protocol today and need a digital signature algorithm, use (in order of preference):
- Ed25519 or Ed448
- ECDSA over NIST P-256 or P-384, with RFC 6979
- ECDSA over NIST P-256 or P-384, without RFC 6979
- RSA (as a last resort)
But most importantly: make sure you have a cryptographer audit your designs.
(Header art by Kyume.)
https://soatok.blog/2020/04/26/a-furrys-guide-to-digital-signature-algorithms/
#crypto #cryptography #DeterministicSignatures #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #FIPS #FIPS186 #FIPSCompliance #RFC6979 #SecurityGuidance

Let’s talk about digital signature algorithms.
Digital signature algorithms are one of the coolest ideas to come out of asymmetric (a.k.a. public-key) cryptography, but they’re so simple and straightforward that most cryptography nerds don’t spend a lot of time thinking about them.
Even though you are more likely to run into a digital signature as a building block (e.g. certificate signatures in TLS) than think about them in isolation (e.g. secure software releases), they’re still really cool and worth learning about.
What’s a Digital Signature?
A digital signature is some string that proves that a specific message was signed by some specific entity in possession of the secret half of an asymmetric key-pair. Digital Signature Algorithms define the process for securely signing and verifying messages with their associated signatures.
For example, if I have the following keypair:
- Secret key:
9080a2c7897faeb8526968161695da0f7b3afa2e8e7d8e8369a85547ab48ea05 - Public key:
482b8d3430445cdad6b5ce59778e09ab59d099120f32d316e881db1a6330390b
I can cryptographically sign the message “Dhole Moments: Never a dull moment!” with the above secret key, and it will generate the signature string: 63629779a31b623486145359c6f1d56602d8d9135e4b17fa2ae3667c8947397decd7ae01bfed08645a429f5dee906e87df4e18eefdfff9acb5b1488c9dec800f.
If you only have the message, signature string, and my public key, you can verify that I signed the message. But, very crucially, you cannot sign messages and convince someone else that they came from me. (With symmetric authentication schemes, such as HMAC, you can.)
A digital signature algorithm is considered secure if, in order for anyone else to pass off a different message as being signed by me, they would need my secret key to succeed. When this assumption holds true, we say the scheme is secure against existential forgery attacks.
How Do Digital Signatures Work?
Simple answer: They generally combine a cryptographic hash function (e.g. SHA-256) with some asymmetric operation, and the details beyond that are all magic.
More complicated answer: That depends entirely on the algorithm in question!

For example, with RSA signatures, you actually encrypt a hash of the message with your secret key to sign the message, and then you RSA-decrypt it with your public key to verify the signature. This is backwards from RSA encryption (where you do the totally sane thing: encrypt with public key, decrypt with secret key).
In contrast, with ECDSA signatures, you’re doing point arithmetic over an elliptic curve (with a per-signature random value).
Yet another class of digital signature algorithms are hash-based signatures, such as SPHINCS+ from the NIST Post-Quantum Cryptography Standardization effort, wherein your internals consist entirely of hash functions (and trees of hash functions, and stream ciphers built with other hash functions).
In all cases, the fundamental principle stays the same: You sign a message with a secret key, and can verify it with a public key.
In the interest of time, I’m not going to dive deep into how each signature algorithm works. That can be the subject of future blog posts (one for each of the algorithms in question).
Quick aside: Cryptographers who stumble across my blog might notice that I deviate from convention a bit. They typically refer to the sensitive half of an asymmetric key pair as a “private key”, but I instead call it a “secret key”.
The main reason for this is that “secret key” can be abbreviated as “sk” and public key can be abbreviated as “pk”, whereas private/public doesn’t share this convenience. If you ever come across their writings and wonder about this discrepancy, I’m breaking away from the norm and their way is more in line with the orthodoxy.
What Algorithms Should I Use?

If you find yourself asking this question, you’re probably dangerously close to rolling your own crypto. If so, you’ll want to hire a cryptographer to make sure your designs aren’t insecure. (It’s extremely easy to design or implement otherwise-secure cryptography in an insecure way.)
Recommended Digital Signature Algorithms
(Update, 2022-05-19): I’ve published a more in-depth treatment of the Elliptic Curve Digital Signature Algorithms a few years after this post was created. A lot of the topics covered by EdDSA and ECDSA are focused on there.
EdDSA: Edwards Curve DSA
EdDSA comes in two variants: Ed25519 (widely supported in a lot of libraries and protocols) and Ed448 (higher security level, but not implemented or supported in as many places).
The IETF standardized EdDSA in RFC 8032, in an effort related to the standardization of RFC 7748 (titled: Elliptic Curves for Security).
Formally, EdDSA is derived from Schnorr signatures and defined over Edwards curves. EdDSA’s design was motivated by the real-world security failures of ECDSA:
- Whereas ECDSA requires a per-signature secret number (
) to protect the secret key, EdDSA derives the per-signature nonce deterministically from a hash of the secret key and message.
- ECDSA with biased nonces can also leak your secret key through lattice attacks. To side-step this, EdDSA uses a hash function twice the size as the prime (i.e. SHA-512 for Ed25519), which guarantees that the distribution of the output of the modular reduction is unbiased (assuming uniform random inputs).
- ECDSA implemented over the NIST Curves is difficult to implement in constant-time: Complicated point arithmetic rules, point division, etc. EdDSA only uses operations that are easy to implement in constant-time.
For a real-world example of why EdDSA is better than ECDSA, look no further than the Minerva attacks, and the Ed25519 designer’s notes on why EdDSA stood up to the attacks.
The security benefits of EdDSA over ECDSA are so vast that FIPS 186-5 is going to include Ed25519 and Ed448.

This is kind of a big deal! The FIPS standards are notoriously slow-moving, and they’re deeply committed to a sunk cost fallacy on algorithms they previously deemed acceptable for real-world deployment.
RFC 6979: Deterministic ECDSA
Despite EdDSA being superior to ECDSA in virtually every way (performance, security, misuse-resistance), a lot of systems still require ECDSA support for the foreseeable future.
If ECDSA is here to stay, we might as well make it suck less in real-world deployments. And that’s exactly what Thomas Pornin did when he wrote RFC 6979: Deterministic Usage of DSA and ECDSA.
(Like EdDSA, Deterministic ECDSA is on its way to FIPS 186-5. Look for it in FIPS-compliant hardware 5 years from now when people actually bother to update their implementations.)
Acceptable Digital Signature Algorithms
ECDSA Signatures
The Elliptic Curve Digital Signature Algorithm (ECDSA) is the incumbent design for signatures. Unlike EdDSA, ECDSA is a more flexible design that has been applied to many different types of curves.
This is more of a curse than a blessing, as Microsoft discovered with CVE-2020-0601: You could take an existing (signature, public key) pair with standard curve, explicitly set the generator point equal to the victim’s public key, and set your secret key to 1, and Windows’s cryptography library would think, “This is fine.”
For this reason, cryptographers were generally wary of proposals to add support for Koblitz curves (including secp256k1–the Bitcoin curve) or Brainpool curves into protocols that are totally fine with NIST P-256 (and maybe NIST P-384 if you need it for compliance reasons).
For that reason, if you can’t use EdDSA or RFC 6979, your fallback option is ECDSA with one of those two curves (secp256r1, secp384r1), and making sure that you have access to a reliable cryptographic random number generator.
RSA Signatures
It’s high time the world stopped using RSA.
Not just for the reasons that Trail of Bits is arguing (which I happen to agree with), but more importantly:
Replacing RSA with EdDSA (or Deterministic ECDSA) also gives teams an opportunity to practice migrating from one cryptography algorithm suite to another, which will probably be a much-needed experience when quantum computers come along and we’re all forced to migrate to post-quantum cryptography.
Encryption is a bigger risk of being broken by quantum computers than signature schemes: If you encrypt data today, a quantum computer 20 years down the line can decrypt it immediately. Conversely, messages that are signed today cannot be broken until after a quantum computer exists.
That being said, if you only need signatures and not encryption, RSA is still acceptable. If you also need encryption, don’t use RSA for that purpose.
If you can, use PSS padding rather than PKCS#1 v1.5 padding, with SHA-256 or SHA-384. But for signatures (i.e. not encryption), PKCS#1 v1.5 padding is fine.
Dishonorable Mention
DSA Signatures
There’s really no point in using classical DSA, when ECDSA is widely supported and has more ongoing attention from cryptography experts.
If you’re designing a system in 2020 that uses DSA, my only question for you is…

Upcoming Signature Algorithms
Although it is far too early to consider adopting these yet, cryptographers are working on new designs that protect against wider ranges of real-world threats.
Let’s briefly look at some of them and speculate wildly about what the future looks like. For fun. Don’t use these yet, unless you have a very good reason to do so.
Digital Signature Research Topics
Hedged Signatures
Above, we concluded that EdDSA and Deterministic ECDSA were generally the best choice (and what I’d recommend for software developers). There is one important caveat: Fault attacks.
A fault attack is when you induce a hardware fault into a computer chip, and thereby interfere with the correct functioning of a cryptography algorithm. This is especially relevant to embedded devices and IoT.
The IETF’s CFRG is investigating the use of additional randomization of messages (rather than randomizing signatures) as a safeguard against leaking secret keys through fault injection.
Of course, the Dhole Cryptography Library (my libsodium wrapper for JavaScript and PHP) already provides a form of Hedged Signatures.
If this technique is proven successful at mitigating fault injection attacks, then libsodium users will be able to follow the technique outlined in Dhole Crypto to safeguard their own protocols against fault attacks. Until then, they’re at least as safe as deterministic EdDSA today.
Threshold ECDSA Signatures
Suppose you have a scenario where you want 3-or-more people to have to sign a message before it’s valid. That’s exactly what Threshold ECDSA with Fast Trustless Setup aspires to provide.
Although this is mostly being implemented in cryptocurrency projects today, the cryptography underpinnings are fascinating. At worst, this will be one good side-effect to come from blockchain mania.
Post-Quantum Digital Signatures
Hash-Based Signatures
The best hash-based signature schemes are based on the SPHINCS design for one simple reason: It’s stateless.
In earlier hash-based digital signatures, such as XMSS, you have to maintain a state of which keys you’ve already used, to prevent attacks. Google’s Adam Langley previously described this as a “huge foot-cannon” for security (although probably okay in some environments, such as an HSM).
Lattice-Based Signatures
There are a lot of post-quantum signature algorithm designs defined over lattice groups, but my favorite lattice-based design is called FALCON. FALCON stands for FAst-Fourier Lattice-based COmpact Signatures Over NTRU.
Sign Here, Please
Who knew there would be so much complexity involved with such a simple cryptographic operation? And we didn’t even dive deep on how any of them work.
That’s the problem with cryptography: It’s a fractal of complexity. The more you know about these topics, the deeper the complexity becomes.
But if you’re implementing a protocol today and need a digital signature algorithm, use (in order of preference):
- Ed25519 or Ed448
- ECDSA over NIST P-256 or P-384, with RFC 6979
- ECDSA over NIST P-256 or P-384, without RFC 6979
- RSA (as a last resort)
But most importantly: make sure you have a cryptographer audit your designs.
(Header art by Kyume.)
https://soatok.blog/2020/04/26/a-furrys-guide-to-digital-signature-algorithms/
#crypto #cryptography #DeterministicSignatures #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #FIPS #FIPS186 #FIPSCompliance #RFC6979 #SecurityGuidance
Earlier this year, Cendyne published A Deep Dive into Ed25519 Signatures, which covered some of the different types of digital signature algorithms, but mostly delved into the Ed25519 algorithm. Truth in advertising.This got me thinking, “Why isn’t there a better comparison of different elliptic curve signature algorithms available online?”
Art: LvJ
Most people just defer to SafeCurves, but it’s a little dated: We have complete addition formulas for Weierstrass curves now, but SafeCurves doesn’t reflect that.
For the purpose of simplicity, I’m not going to focus on a general treatment of Elliptic Curve Cryptography (ECC), which includes pairing-based cryptography, Elliptic-Curve Diffie-Hellman, and (arguably) isogeny cryptography.
Instead, I’m going to focus entirely on elliptic curve digital signature algorithms.
Note: The content of this post is a bit lower-level than most programmers ever need to be concerned with. If you’re a programmer and interested in learning cryptography, start here. If you’re looking for library recommendations, libsodium is a good safe default.
Compliance Rules Everything Around Me
If you have to meet some arbitrary compliance requirements (i.e. FIPS 140-3, CNSA, etc.), your decision is already made for you, and you shouldn’t waste your time reading blogs like this that will only get your hopes up about the options available to you.Choose the option your compliance officer demands, and hope it’s good enough.
“Sure, let me check that box.”
Art: LvJElliptic Curves for Signature Algorithms
Let’s start with the same curve Cendyne analyzed: Ed25519.Ed25519 (EdDSA, Curve25519)
Ed25519 is one of the two digital signature algorithms today that use the EdDSA algorithm framework. The other is Ed448, which targets a higher security level (224-bit vs 128-bit) but is also slower and uses SHAKE256 (which is overkill and not great for performance).Ed25519 is a safe default choice for most applications where a digital signature is appropriate, for many reasons:
- Ed25519 uses deterministic nonces, which means you’re severely unlikely to ever reproduce the Sony ECDSA k-reuse bug in your system.
The deterministic nonce is calculated from the SHA512 hash of the secret key and message. Two invocations tocrypto_sign_ed25519()with the same message and secret key will produce the same signature, but the intermediate nonce value is never revealed to an attacker.- Ed25519 includes the public key in the data hashed to produce the signature (more specifically s from the (R,s) pair). This offers a property that ECDSA lacks: Exclusive Ownership. I’ve written about this property before.
Without Exclusive Ownership, it’s possible to create a single signature value that’s valid for multiple different (message, public key) pairs.Years ago, there would have an additional list item: Ed25519 uses Edward Curves, which have complete addition formulas and are therefore safer to implement in constant-time than Weierstrass curves (i.e. the NIST curves). However, we now have complete addition formulas for Weierstrass curves, so this has become a moot point (assuming your implementation uses complete addition formulas).
Ed25519 targets the 128-bit security level.
Why Not Use Ed25519?
There is one minor pitfall of Ed25519 that makes it unsuitable for esoteric uses (say, Ring Signature Schemes or zero-knowledge proofs): Ed25519 is not a prime-order group; it has a cofactor h = 8. This detail famously created a double-spend vulnerability in all CryptoNote-based cryptocurrencies (including Monero).For systems that want the security of Ed25519 and its various well-studied implementations, but still need a prime-order group for their protocol, cryptographers have developed the Ristretto Group to meet your needs.
If you’re working on embedded systems, the determinism inherent to EdDSA might be undesirable due to the possibility of fault attacks. You can use a hedged variant of Ed25519 to mitigate this risk.
Additionally, Ed25519 is not approved for many government applications, although it did make the latest draft revision of FIPS 186 in 2019. If you care about compliance (see above), you cannot use Ed25519. Yet.
A niche Internet meme for cryptography engineers
Guidance for Ed25519
Unless legally prohibited, Ed25519 should be your default choice, unless you need a prime-order group. In that case, build your desired protocol atop Ristretto255.If you’re not sure if you need a prime-order group, you probably don’t. It’s a specialized requirement for uncommon use cases (ring signatures, password authenticated key exchange protocols, zero-knowledge proofs, etc.).
Art: LvJ
The Bitcoin Curve (ECDSA, secp256k1)
Secp256k1 is a Koblitz curve, which is a special case of Weierstrass curves that are more performant when used in binary fields, of the form,. This curve is almost exclusively used in cryptocurrency software.
There is no specified reason why Bitcoin chose secp256k1 over another elliptic curve at the time of its inception, but we can speculate:
The author was a pseudonymous contributor to the Metzdowd mailing list for cypherpunks, and probably didn’t trust the NIST curves. Since Ed25519 didn’t exist at the time, the only obvious choice for a hipster elliptic curve parameter selection was to rely on the SECG recommendations, which specify the NIST and Koblitz curves. If you cross the NIST curves off the list, only the Koblitz curves remained.
Therefore, the selection of secp256k1 is likely an artefact of computer history and not a compelling reason to select secp256k1 in new designs. Please look elsewhere.
Fact: Imgflip didn’t have a single secp256k1 meme until I made this one.
Secp256k1 targets the 128-bit security level.
Guidance for secp256k1
Don’t bother, there are better options. (i.e. Ed25519)If you’re writing software for a cryptocurrency-related project, and you feel compelled to use secp256k1 for the sake of reducing your code footprint, please strongly consider the option of burning everything to the proverbial ground.
Cryptocurrency sucks!
Art: SwizzCryptocurrency Aside, Why Avoid Secp256k1?
As we noted above, secp256k1 isn’t widely used outside of cryptocurrency.As a direct consequence of this (as we’ll discuss in the NIST P-256 section), most cryptography libraries don’t offer optimized, side-channel-resistant implementations of secp256k1; even if they do offer optimized implementations of NIST P-256.
(Meanwhile, Ed25519 is designed to be side-channel and misuse-resistant, partly due to its Schnorr construction and constant-time ladder for scalar multiplication, so any library that implements Ed25519 is overwhelmingly likely to be constant-time.)
Therefore, any secp256k1 library for most programming languages that isn’t an FFI wrapper for libsecp256k1 will have worse performance than the other 256-bit curves.
https://twitter.com/bascule/status/1320183684935290882
Additionally, secp256k1 implementations are often a source of exploitable side-channels that permit attackers to pilfer your secret keys.
The previously linked article was about BouncyCastle’s implementation (which covers Java and .NET), but there’s still plenty of secp256k1 implementations that don’t FFI libsecp256k1.
From a quick Google Search:
- Python (uses EEA rather than Binary GCD for modular inverse)
- Go (uses Numbers, which weren’t designed for cryptography)
- PHP (uses GMP, which isn’t constant-time)
- JavaScript (calls here, which uses bn.js, which isn’t constant-time)
If you’re using secp256k1, and you’re not basing your choice on cybercash-interop, you’re playing with fire at the implementation and ecosystem levels–even if there are no security problems with the Koblitz curve itself.
You are much better off choosing any different curve than secp256k1 if you don’t have a Bitcoin/Ethereum/etc. interoperability requirement.
“No thanks, I use Ed25519.”
Art: LvJNIST P-256 (ECDSA, secp256r1)
NIST P-256 is the go-to curve to use with ECDSA in the modern era. Unlike Ed25519, P-256 uses a prime-order group, and is an approved algorithm to use in FIPS-validated modules.Most cryptography libraries offer optimized assembly implementations of NIST P-256, which makes it less likely that your signing operations will leak timing information or become a significant performance bottleneck.
P-256 targets the 128-bit security level.
Why Not Use P-256?
Once upon a time, P-256 was riskier than Ed25519 (for signatures) and X25519 (for Diffie-Hellman), due to the incomplete addition formulas that led to timing-leaky implementations.If you’re running old software, you may still be vulnerable to timing attacks that can recover your ECDSA secret key. However, there is a good chance that you’re on a modern and secure implementation in 2022, especially if you’re outsourcing this to OpenSSL or its derivatives.
ECDSA requires a secure randomness source to sign data. If you don’t have one available, and you sign anything, you’re coughing up your secret key to any attacker capable of observing multiple signatures.
Guidance for P-256
P-256 is an acceptable choice, especially if you’re forced to cope with FIPS and/or the CNSA suite requirements when using cryptography.Of course, if you can get away with Ed25519, use Ed25519 instead.
If you use P-256, make sure you’re using it with SHA-256. Some implementations may default to something weaker (e.g. SHA-1).
If you’re also going to be performing ECDH with P-256, make sure you use compressed points. There used to be a patent; it died in 2018.
If you can afford it, make sure you use deterministic ECDSA (RFC 6979) or hedged signatures (if fault attacks are relevant to your threat model).
Art: LvJ
NIST P-384 (ECDSA, secp384r1)
NIST P-384 has a larger field than the curves we’ve previously examined, which allows P-384 to target the 192-bit security level. That’s the primary reason why anyone would choose P-384.Naturally, elliptic curve security is more complicated than merely security against the Elliptic Curve Discrete Logarithm Problem (ECDLP).
P-384 is most often paired with SHA-384, which is the most widely used flavor of the SHA-2 family hash functions that isn’t susceptible to length-extension attacks. (There are also truncated SHA-512 variants specified later, but that’s also what SHA-384 is under-the-hood.)
If you’re aiming to build a “secure-by-default” tool for a system that the US government might one day become a customer of, with minimal cryptographic primitive choice, using NIST P-384 with SHA-384 makes for a reasonably minimalistic bundle.
Why Not Use P-384?
Unlike P-256, most P-384 implementations don’t use constant-time, optimized, and/or formally verified assembly code. (Notable counter-examples: AWS-LC and Go x/crypto.)Like P-256, P-384 also requires a secure randomness source to sign data. If you aren’t providing one, expect your signing key to end up on fail0verflow one day.
Guidance for P-384
If you use P-384, make sure you’re using it with SHA-384.The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.
Art: Kyume
NIST P-521 (ECDSA, secp521r1)
Biggest curve is best curve! — the cluelesshttps://www.youtube.com/watch?v=i_APoSfCYwU
Systems that choose P-521 often have an interesting threat model, even though said threat model is rarely formally specified.
It’s overwhelmingly likely that what eventually breaks the 256-bit elliptic curves will also break P-521 in short order: Cryptography Relevant Quantum Computers.
The only thing P-521 does against CRQCs that P-256 doesn’t is require more quantum memory. If you’re worried about QRQCs, you might want to look into hybrid post-quantum signature schemes.
If you’re choosing P-521 in your designs, you’re basically saying, “I want to have 256 bits of asymmetric cryptographic security, come hell or high water!” even though the 128-bit security level is likely just fine for your actual threats.
Aside: P-521 and 512-bit ECC Security
P-521 is not a typo, although people sometimes think it is. P-521 uses the Mersenne primeinstead of a 512-bit near-Mersenne prime.
This has led to an unfortunate trend in cryptography media to map ECC key sizes to symmetric security levels that misleads people as to the relationship between the two. For example:
Regrettably, this is misleading, because plotting the ECC Key Size versus equivalent Symmetric Security isn’t a how ECDLP security works. The ratio of the exponents involved is totally linear; it doesn’t suddenly increase beyond 384-bit curves for a mysterious mathematical reason.
- 256-bit Curves target the 128-bit security level
- 384-bit Curves target the 192-bit security level
- 512-bit Curves target the 256-bit security level
- 521-bit Curves actually target the 260-bit security level, but that meets or exceeds the 256-bit security level, so that’s how the standards are interpreted
The reason for this boils down entirely to the best attack against the Elliptic Curve Discrete Logarithm Problem: Pollard’s Rho, which recovers the secret key from an
-bit public key (which has a
search space) in
guesses.
Taking the square root of a number is the same as halving its exponent, so the security level is half:
.
Takeaway: If someone tells you that you need a 521-bit curve to meet the 256-bit security level, they are mistaken and it’s not their fault.
Art: Harubaki
Why Not Use P-521?
It’s slow. Much slower than P-256 and Ed25519. Modestly slower than P-384.Unlike P-384, you’re less likely to find an optimized, constant-time P-521 implementation.
Guidance for P-521
First, make a concerted effort to figure out the motivation for P-521 in your designs. Chances are, someone is putting too much emphasis on the wrong things for security.If you use P-521, make sure you’re using it with SHA-512.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.
Art: LvJ
Ed448 (EdDSA, Curve448)
Ed448 is the P-521 of the Edwards curves: It mostly exists to give standards committees a psychological comfort for the unlikely event that 256-bit ECC is desperately broken but ECC larger than 384 bits is somehow still safe.https://twitter.com/dchest/status/703017144053833728
The very concept of having multiple “security levels” for raw cryptography primitives is mostly an artefact of the historical military roots of cryptography, rather than a serious consideration in the modern world.
Unfortunately, this leads to implementations that prioritize runtime algorithm selection negotiation, which maximizes the risk of protocol-level vulnerabilities. See also: JWT.
Ed448 was specified to use SHAKE256, which is a needlessly conservative decision which leads to an unnecessary performance bottleneck.
Why Not Use Ed448?
Aside from the performance hit mentioned previously, there’s no compelling reason to avoid Ed448 that isn’t also true of either Ed25519 or P-384.Guidance for Ed448
If you want more speed, go with Ed25519. In addition to being faster, Ed25519 is also very widely supported.If you need a prime-order field, use Decaf with Ed448 or consider P-384.
The Brainpool Curves
The main motivation for the Brainpool curves is that the NIST curves were not generated in a “verifiable pseudo-random way”.The only reasons you’d ever want to support the Brainpool curves include:
- You think the NIST curves are somehow backdoored by the NSA
- You don’t appreciate small attack surfaces in cryptography libraries
- The German government told you to (see: compliance)
Most of the advice for the NIST Curves at each security level can be copy/pasted for the Brainpool curves, with one important caveat:
When considering real-world implementations, Brainpool curves are more likely to use the general purpose Big Number procedures (which aren’t always constant-time), rather than optimized assembly code, than the NIST curves are.
Therefore, my general guidance for the Brainpool curves is simply:
- Proceed at your own peril
- Consider hiring a cryptography engineer to study the implementation you’re relying on, especially with regard to timing attacks
Me when I hear “brainpool”
Art: LvJRe-Examining the SafeCurves Criteria
Here’s a 2022 refresh of the SafeCurves criteria for all of the curves considered by this blog post.
SafeCurve Criteria Relevance to the Curves Listed Above Fields All relevant curves satisfy the requirements Equations All relevant curves satisfy the requirements Base Points All relevant curves satisfy the requirements Rho All relevant curves satisfy the requirements Transfers All relevant curves satisfy the requirements Discriminants Only secp256k1 doesn’t satisfy the requirements (out of the curves listed in this blog post) Rigidity The NIST curves do not meet this requirement.
If you care about whether or not the standards were manipulated to insert a backdoor, rigidity matters to you. Otherwise, it’s not a deal-breaker.Ladders While a Montgomery ladder is beneficial for speed and implementation security, it isn’t strictly speaking required.
This is an icing-on-the-cake consideration.Twists The only curve listed above that doesn’t meet the requirement is the 256-bit Brainpool curve (brainpoolp256t1). Completeness All relevant curves satisfy the requirements, as of 2015.
SafeCurves is out of date here.Indistinguishability All relevant curves satisfy the requirements, as of 2014. SafeCurves continues to be a useful resource, especially if you stray from the guidance on this page.
For example: You wouldn’t want to use pairing-friendly curves for general purpose ECC digital signatures, because they’re suitable for specialized problems. SafeCurves correctly recommends not using BN(2,254).
However, SafeCurves is showing its age in 2022. BN curves still end up in digital signature protocol standards even though BLS-12-381 is clearly a better choice.
The Internet would benefit greatly for an updated SafeCurves that focuses on newer elliptic curve algorithms.
Art: Scruff
TL;DR
Ed25519 is great. NIST P-256 and P-384 are okay (with caveats). Anything else is questionable, and their parameter selection should come with a clear justification.https://soatok.blog/2022/05/19/guidance-for-choosing-an-elliptic-curve-signature-algorithm-in-2022/
#asymmetricCryptography #BrainpoolCurves #cryptography #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #ellipticCurveCryptography #P256 #P384 #P521 #secp256k1 #secp256r1 #secp384r1 #secp521r1 #SecurityGuidance

A paper was published on the IACR’s ePrint archive yesterday, titled LadderLeak: Breaking ECDSA With Less Than One Bit of Nonce Leakage.
The ensuing discussion on /r/crypto led to several interesting questions that I thought would be worth capturing and answering in detail.
What’s Significant About the LadderLeak Paper?
This is best summarized by Table 1 from the paper.
The paper authors were able to optimize existing attacks exploiting one-bit leakages against 192-bit and 160-bit elliptic curves. They were further able to exploit leakages of less than one bit in the same curves.
How Can You Leak Less Than One Bit?
We’re used to discrete quantities in computer science, but you can leak less than one bit of information in the case of side-channels.
Biased modular reduction can also create a vulnerable scenario: If you know the probability of a 0 or a 1 in a given position in the bit-string of the one-time number (i.e. the most significant bit) is not 0.5 to 0.5, but some other ratio (e.g. 0.51 to 0.49), you can (over many samples) conclude a probability of a specific bit in your dataset.
If “less than one bit” sounds strange, that’s probably our fault for always rounding up to the nearest bit when we express costs in computer science.
What’s the Cost of the Attack?
Consult Table 3 from the paper for empirical cost data: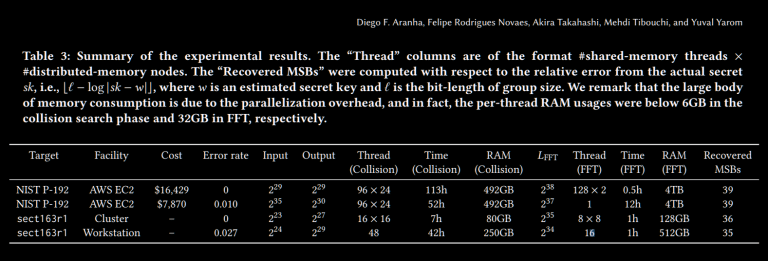
How Devastating is LadderLeak?
First, it assumes a lot of things:
- That you’re using ECDSA with either sect163r1 or secp192r1 (NIST P-192). Breaking larger curves requires more bits of bias (as far as we know).
- That you’re using a cryptography library with cache-timing leaks.
- That you have a way to measure the timing leaks (and not just pilfer the ECDSA secret key; i.e. in a TPM setup). This threat model generally assumes some sort of physical access.
But if you can pull the attack off, you can successfully recover the device’s ECDSA secret key. Which, for protocols like TLS, allow an attacker to impersonate a certificate-bearer (typically the server)… which is pretty devastating.
Is ECDSA Broken Now?
Non-deterministic ECDSA is not significantly more broken with LadderLeak than it already was by other attacks. LadderLeak does not break the Internet.
Fundamentally, LadderLeak doesn’t really change the risk calculus. Bleichenbacher’s attack framework for solving the Hidden Number Problem using Lattices was already practical, with sufficient samples.
There’s even a CryptoPals challenge about these attacks.
As an acquaintance put it, the authors made a time-memory trade-off with a leaky oracle. It’s a neat result worthy of publication, but we aren’t any minutes closer to midnight with this revelation.
Is ECDSA’s k-value Really a Nonce?
Ehhhhhhhhh, sorta.

Nonce in cryptography has always meant “number that must be used only once” (typically per key). See: AES-GCM.
Nonces are often confused for initialization vectors (IVs), which in addition to a nonce’s requirements for non-reuse must also be unpredictable. See: AES-CBC.
However, nonces and IVs can both be public, whereas ECDSA k-values MUST NOT be public! If you recover the k-value for a given signature, you can recover the secret key too.
That is to say, ECDSA k-values must be all of the above:
- Never reused
- Unpredictable
- Secret
- Unbiased
They’re really in a class of their own.
For that reason, it’s probably better to think of the k-value as a per-signature key than a simple nonce. (n.b. Many cryptography libraries actually implement them as a one-time ECDSA keypair.)
What’s the Difference Between Random and Unpredictable?
The HMAC-SHA256 output of a message under a secret key is unpredictable for anyone not in possession of said secret key. This value, though unpredictable, is not random, since signing the same message twice yields the same output.
A large random integer when subjected to modular reduction by a non-Mersenne prime of the same magnitude will be biased towards small values. This bias may be negligible, but it makes the bit string that represents the reduced integer more predictable, even though it’s random.
What Should We Do? How Should We Respond?
First, don’t panic. This is interesting research and its authors deserve to enjoy their moment, but the sky is not falling.
Second, acknowledge that none of the attacks are effective against EdDSA.
If you feel the urge to do something about this attack paper, file a support ticket with all of your third-party vendors and business partners that handle cryptographic secrets to ask them if/when they plan to support EdDSA (especially if FIPS compliance is at all relevant to your work, since EdDSA is coming to FIPS 186-5).
Reason: With increased customer demand for EdDSA, more companies will adopt this digital signature algorithm (which is much more secure against real-world attacks). Thus, we can ensure an improved attack variant that actually breaks ECDSA doesn’t cause the sky to fall and the Internet to be doomed.
(Seriously, I don’t think most companies can overcome their inertia regarding ECDSA to EdDSA migration if their customers never ask for it.)
https://soatok.blog/2020/05/26/learning-from-ladderleak-is-ecdsa-broken/
#crypto #cryptography #digitalSignatureAlgorithm #ECDSA #ellipticCurveCryptography #LadderLeak
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Art by Khia.
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting
(at 50% probability) blocks.
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
you expect from AES.
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.This is because Grover’s quantum search algorithm can search
unsorted items in
time, which can be used to reduce the total number of possible secrets from
to
. This effectively cuts the security level, expressed in bits, in half.
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
(plaintext, key) pairs that produce any given ciphertext block.
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
times as many AES-256 keys as there are possible plaintext/ciphertexts. Keep this in mind for AES-GCM.
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
This is unacceptable!
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
: A number that must only be used once).
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
The deeper you look into AES-GCM’s design, the harder you will feel this sticker.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called. This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
This is often sold as an advantage: Reusingallows for better performance. However, it makes GCM brittle: Reusing a nonce allows an attacker to recover H and then forge messages forever. This is called the “forbidden attack”, and led to real world practical breaks.
Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.If we assume AES is well-behaved, we can deduce that there are approximately
different 256-bit keys that will map a single plaintext block to a single ciphertext block.
This is trivial to calculate. Simply divide the number of possible keys (
) by the number of possible block states (
) to yield the number of keys that produce a given ciphertext for a single block of plaintext:
.
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
.
This means there are approximately
independent keys that will map a given all-zero plaintext block to an arbitrarily chosen value of
(if we assume AES doesn’t have weird biases).
Credit: Harubaki
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection ofas a 128-bit pseudorandom function, rather than a 128-bit permutation. As a result, you an expect a collision with 50% probability after only
different keys are selected.
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a
collision risk. So that means our safety limit is actually
different AES keys before you have to worry about
reuse.
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of
different AES keys, you have to either accept the risk or stop using AES-GCM.
If you have a billion users (
), the safety limit is breached after
AES keys per user (approximately 262,000).
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.is used for block multiplication, and
(the value of
with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.
The arrow highlighted with green is HF.
It’s tempting to think that a reuse of
isn’t a concern because
will necessarily be randomized, which prevents an attacker from observing when
collides. It’s certainly true that the single-block collision risk discussed previously for
will almost certainly not also result in a collision for
. And since
isn’t reused unless a nonce is reused (which also leaks
directly), this might seem like a non-issue.
Art by Khia.
However, it’s straightforward to go from a condition of
reuse to an adaptive chosen-ciphertext attack.
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- Use your knowledge of
, the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of
for a given nonce.
- Calculate a new authentication tag for a chosen ciphertext using
and your candidate
value, then replay it into the target system.
While the blinding offered by XORing the final output with
is sufficient to stop
from being leaked directly, the protection is one-way.
Ergo, a collision in
is not sufficiently thwarted by
.
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
is
, and finding an untargeted collision requires being able to observe more than
different sessions, and somehow distinguish when
collides.
As a user, you know that after
different keys, you’ve crossed the safety boundary for avoiding
collisions. But as an attacker, you need
bites at the apple, not
. Additionally, you need some sort of oracle or distinguisher for when this happens.
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
is challenging to work with. You would need the computational and data storages of a major cloud service provider to even think about pulling the attack off.
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
bytes long, under a given (key, nonce) pair.
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
messages.
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atrandom nonces, which represents a collision probability of one in 4 billion.
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
I’m glad you asked!
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
messages (for the same collision probability as AES-GCM).
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography

Canonicalization Attacks occur when a protocol that feeds data into a hash function used in a Message Authentication Code (MAC) or Digital Signature calculation fails to ensure some property that’s expected of the overall protocol.
The textbook example of a canonicalization attack is the length-extension attack against hash functions such as MD5–which famously broke the security of Flickr’s API signatures.
But there’s a more interesting attack to think about, which affects the design of security token/envelope formats (PASETO, DSSE, etc.) and comes up often when folks try to extend basic notions of authenticated encryption (AE) to include additional authenticated (but unencrypted) data (thus yielding an AEAD mode).
Let’s start with a basic AE definition, then extend it to AEAD poorly, then break our extension. Afterwards, we can think about strategies for doing it better.
Turning CTR+HMAC into AEAD
Signal uses AES-CBC then HMAC-SHA2 to encrypt messages between mobile devices.
We often refer to this shape as “CBC+HMAC” (although this is a few typos away from being confused with a very different idea called CBC-MAC).
When CBC+HMAC is used with the AES block cipher with 256-bit keys and HMAC-SHA2, it becomes AES-256-CBC+HMAC-SHA256. What a mouthful!

(Art by Lynx vs Jackalope)
In modern designs, AES-CTR is often preferable to AES-CBC, since you don’t have to deal with padding (or padding oracles).
Most systems these days prefer GCM over CBC+HMAC or CTR+HMAC. I don’t like AES-GCM (especially if your use-case is “support platforms without hardware acceleration”), but it’s hardly the worst choice for most applications. AES-GCM is a dedicated AEAD mode, while CBC+HMAC and CTR+HMAC merely provide AE.
Why Does Additional Data Matter?

The main purpose of Additional Data (the AD in AEAD) is to bind an encrypted payload (ciphertext + authentication tag) to a given context. This is extremely helpful in mitigating Confused Deputy attacks.
Critically, this additional data is not encrypted. (At least, on this level; it’s probably wise to communicate over HTTPS!)
Naive CTR+HMAC to AEAD Extension
In a normal CTR+HMAC definition, your algorithm looks something like this:
- Generate a random nonce equal to the block size of your block cipher. (16 bytes for AES.)
- Encrypt your message with AES-CTR, using the given key and IV.
- Calculate the HMAC-SHA2 output of the IV followed by the ciphertext from step 2.
- Return IV, Ciphertext, MAC.
Decryption basically runs steps 3 and 2 in reverse: Recalculate the MAC (in constant-time!), decrypt ciphertext, return plaintext.
The most obvious way to extend this design to support additional authenticated data is to append it to the ciphertext.
This yields the following updated protocol:
- Generate a random nonce equal to the block size of your block cipher. (16 bytes for AES.)
- Encrypt your message with AES-CTR, using the given key and nonce.
- Calculate the HMAC-SHA2 output of the IV followed by the ciphertext from step 2, then the additional authenticated data.
- Return IV, Ciphertext, MAC.
Suffice to say, this is not a secure construction.
The Canonicalization Attack
Let’s say you built this extended protocol to encrypt a payload that looks like a URI string, but wanted to bind the token to a given browser session, so you use the HTTP User-Agent header as the AAD.
When you generate a token, you might produce the following:
const crypto = require('crypto');function splitKey(key) { let hmac; hmac = crypto.createHmac('sha256', key); hmac.update('encrypt-key'); let Ek = hmac.digest(); hmac = crypto.createHmac('sha256', key); hmac.update('hmac-key'); let Ak = hmac.digest(); return [Ek, Ak];}function encryptWithContext(plaintext, aad, key) { let [encKey, authKey] = splitKey(key); console.log(encKey, authKey); let nonce = crypto.randomBytes(16); const aes = crypto.createCipheriv('aes-256-ctr', encKey, nonce); const ciphertext = aes.update(plaintext); aes.final(); // Pay attention to this part: const hmac = crypto.createHmac('sha256', authKey); hmac.update(nonce); hmac.update(ciphertext); hmac.update(aad); return [nonce, ciphertext, hmac.digest()];}let plaintext = [ 'expires=1630223780', 'access_group=1234', 'subject=auth-v2.example.com', 'restrictions=on'].join('&');// expires=1630223780&access_group=1234&subject=auth-v2.example.com&restrictions=on// const key = crypto.randomBytes(32);let [nonce, ciphertext, tag] = encryptWithContext(plaintext, userAgent, key);
So here’s the clever attack: If you can shift bytes from the payload into the prefix of your User-Agent string, they’ll produce the same HMAC tag.
Attackers can truncate as much of the payload as they want by prepending it to the User-Agent included in their HTTP request.
You can even turn this:
expires=1630223780&access_group=1234&subject=auth-v2.example.com&restrictions=on
…into this:
expires=1630223780&access_group=1234&subject=auth-v2.example.com
…without invalidating the existing authentication tag–just by ensuring that the last 16 bytes of ciphertext are prepended to your User-Agent and removed from the payload.
More broadly, any time you have a multi-part message being fed into a hash function, if you aren’t careful with how you feed it into the hash function, you can induce trivial collisions.
See also: Iota’s Kerl hash function.
This is obviously true, because hash functions are deterministic: The same input will always produce the same output. If you can control one or more parts of a multi-part message, you can collide the input–thereby creating a collision in the output.
This can affect any protocol that depends on hash functions, but most obviously, HMAC and Digital Signature algorithms are in scope.
But what does “being careful” look like? Let’s look at a safe example.
Pre-Authentication Encoding (PAE)
Earlier I had mentioned PASETO and DSSE. They both have this notion of a “PAE” algorithm which aims to prevent canonicalization attacks.
PASETO’s definiton for PAE is as follows:
function LE64(n) { var str = ''; for (var i = 0; i < 8; ++i) { if (i === 7) { // Clear the MSB for interoperability n &= 127; } str += String.fromCharCode(n & 255); n = n >>> 8; } return str;}function PAE(pieces) { if (!Array.isArray(pieces)) { throw TypeError('Expected an array.'); } var count = pieces.length; var output = LE64(count); for (var i = 0; i < count; i++) { output += LE64(pieces.length); /*** Soatok Note: This JS pseudocode incorrectly assumes strings, rather than buffers. It's only meant to illustrate the idea. In real implementations, don't join Buffers with +. ***/ output += pieces[i]; } return output;}
What this does (with all lengths as 64-bit unsigned integers, serialized as 8 bytes):
- Prepend the number of parts being hashed.
- For each part, first prefix its length, then its value.
This is an obvious mitigation for canonicalization attacks:
- If you feed in a different number of pieces, the count (the first 8 bytes) will differ.
- If you try to move data from one piece to another, you’ll produce different lengths for both pieces, which will not yield an input collision to the hash function.
However, it’s important that both mechanism are in play to guarantee security:
- Without the length prefixes, we’re no different than the CTR+HMAC extension we defined above.
- Without the count prefix, it’s possible to drop pieces and then include a dummy “length” in the payload of others to create an input collision.
What’s an Input Collision?
First, you need to know what a collision attack is.
Consider a hash function, H(). If you can identify any two input messages (m1, m2) such that H(m1) = H(m2), you’ve found a collision in the output of the hash function.
An input collision is dumber than that.
If m1 is constructed from multiple segments with different meanings, you don’t need an m2. Just find multiple ways (the collisions) to result in the same m1 value (the input).
That’s what we did earlier when we shifted bytes from the ciphertext to the user agent.
DSSE Leaves Me Dizzy
It should come as no surprise that I find DSSE’s definition of PAE to be somewhat bizarre.
PAE(type, body) = "DSSEv1" + SP + LEN(type) + SP + type + SP + LEN(body) + SP + body+ = concatenationSP = ASCII space [0x20]"DSSEv1" = ASCII [0x44, 0x53, 0x53, 0x45, 0x76, 0x31]LEN(s) = ASCII decimal encoding of the byte length of s, with no leading zeros
The only thing that saves them from canonicalization attacks is that the number of pieces is constant.
If the number of pieces was variable (e.g. if the KEYID was optionally included in the signature, but they forgot to always include a hard-coded 0 length if it was absent), you could defeat their flavor of PAE by constructing two different messages that produce the same hash in the digital signature algorithm.
This is because the number of pieces isn’t included in the DSSE definition. (If they ever support a variable number of components, and fail to include the count in the signature, they’ll be vulnerable.)
Amusingly, the rationale page for DSSE using PAE states:
- Why use PAE?
- Because we need an unambiguous way of serializing two fields, payloadType and payload. PAE is already documented and good enough. No need to reinvent the wheel.
…Yet, they didn’t actually [i]use the “already documented and good enough” definition of PAE from PASETO.

(Art by Lynx vs Jackalope)
Fixing AES-CTR+HMAC with PAE
This is pretty straightforward patch:
function encryptWithContext(plaintext, aad, key) { let [encKey, authKey] = splitKey(key); console.log(encKey, authKey); let nonce = crypto.randomBytes(16); const aes = crypto.createCipheriv('aes-256-ctr', encKey, nonce); const ciphertext = aes.update(plaintext); aes.final(); // Pay attention to this part: const hmac = crypto.createHmac('sha256', authKey);- hmac.update(nonce);- hmac.update(ciphertext);- hmac.update(aad);+ hmac.update(PAE([nonce, ciphertext, aad])); return [nonce, ciphertext, hmac.digest()]; }
The only conceivable way to attack this design is to aim for an integer overflow, which will require sending at least 2^63 bytes–at which point, you’re more likely to DDoS the target than succeed.
Wrapping Up
Canonicalization Attacks broadly aren’t well-understood or widely appreciated risks with cryptography protocol design outside of specialist circles (although many application security folks are at least aware of specific instances, i.e. Length Extension).
Part of the reason for this lack of knowledge transfer is that all of the AEAD modes defend against it by design, and most artisanal authenticated encryption constructions don’t bother with additional authenticated data, and most home-made cryptography protocols don’t even authenticate their ciphertexts correctly, and …
You get the point, I hope. There’s unaddressed concerns all the way down. Expecting people who aren’t specialized experts in this specific field to get all of them right is frankly unreasonable. In practice, outside of cryptography, canonicalization either doesn’t matter or there’s something else wrong that’s far more urgent.
https://soatok.blog/2021/07/30/canonicalization-attacks-against-macs-and-signatures/
#collisionAttacks #cryptographicHashFunction #cryptography #digitalSignatureAlgorithm #DSSE #HMAC #lengthExtensionAttacks #MACs #PASETO #SecurityGuidance
This is the first entry in a (potentially infinite) series of dead end roads in the field of cryptanalysis.Cryptography engineering is one of many specialties within the wider field of security engineering. Security engineering is a discipline that chiefly concerns itself with studying how systems fail in order to build better systems–ones that are resilient to malicious acts or even natural disasters. It sounds much simpler than it is.
If you want to develop and securely implement a cryptography feature in the application you’re developing, it isn’t enough to learn how to implement textbook descriptions of cryptography primitives during your C.S. undergrad studies (or equivalent). An active interest in studying how cryptosystems fail is the prerequisite for being a cryptography engineer.
Thus, cryptography engineering and cryptanalysis research go hand-in-hand.
Pictured: How I feel when someone tells me about a novel cryptanalysis technique relevant to the algorithm or protocol I’m implementing. (Art by Khia.)
If you are interested in exploring the field of cryptanalysis–be it to contribute on the attack side of cryptography or to learn better defense mechanisms–you will undoubtedly encounter roads that seem enticing and not well-tread, and it might not be immediately obvious why the road is a dead end. Furthermore, beyond a few comparison tables on Wikipedia or obscure Stack Exchange questions, the cryptology literature is often sparse on details about why these avenues lead nowhere.
So let’s explore where some of these dead-end roads lead, and why they stop where they do.
(Art by Kyume.)
Length Extension Attacks
It’s difficult to provide a better summary of length extension attacks than what Skull Security wrote in 2012. However, that only addresses “What are they?”, “How do you use them?”, and “Which algorithms and constructions are vulnerable?”, but leaves out a more interesting question: “Why were they even possible to begin with?”An Extensive Tale
Tale, not tail! (Art by Swizz.)
To really understand length extension attacks, you have to understand how cryptographic hash functions used to be designed. This might sound intimidating, but we don’t need to delve too deep into the internals.
A cryptographic hash function is a keyless pseudorandom transformation from a variable length input to a fixed-length output. Hash functions are typically used as building blocks for larger constructions (both reasonable ones like HMAC-SHA-256, and unreasonable ones like my hash-crypt project).
However, hash functions like SHA-256 are designed to operate on sequential blocks of input. This is because sometimes you need to stream data into a hash function rather than load it all into memory at once. (This is why you can sha256sum a file larger than your available RAM without crashing your computer or causing performance headaches.)
A streaming hash function API might look like this:
class MyCoolHash(BaseHashClass): @staticmethod def init(): """ Initialize the hash state. """ def update(data): """ Update the hash state with additional data. """ def digest(): """ Finalize the hash function. """ def compress(): """ (Private method.) """
To use it, you’d callhash = MyCoolHash.init()and then chain togetherhash.update()calls with data as you load it from disk or the network, until you’ve run out of data. Then you’d calldigest()and obtain the hash of the entire message.There are two things to take away right now:
- You can call
update()multiple times, and that’s valid.- Your data might not be an even multiple of the internal block size of the hash function. (More often than not, it won’t be!)
So what happens when you call
digest()and the amount of data you’ve passed toupdate()is not an even multiple of the hash size?For most hash functions, the answer is simple: Append some ISO/IEC 7816-4 padding until you get a full block, run that through a final iteration of the internal compression function–the same one that gets called on
update()–and then output the current internal state.Let’s take a slightly deeper look at what a typical runtime would look like for the MyCoolHash class I sketched above:
hash = MyCoolHash.init()
- Initialize some variables to some constants (initialization vectors).
hash.update(blockOfData)
- Start with any buffered data (currently none), count up to 32 bytes. If you’ve reached this amount, invoke
compress()on that data and clear the buffer. Otherwise, just append blockOfData to the currently buffered data.- For every 32 byte of data not yet touched by
compress(), invokecompress()on this block (updating the internal state).- If you have any leftover bytes, append to the internal buffer for the next invocation to process.
hash.update(moreData)
- Same as before, except there might be some buffered data from step 2.
output = hash.digest()
- If you have any data left in the buffer, append a 0x80 byte followed by a bunch of 0x00 bytes of padding until you reach the block size. If you don’t, you have an entire block of padding (0x80 followed by 0x00s).
- Call
compress()one last time.- Serialize the internal hash state as a byte array or hexadecimal-encoded string (depending on usage). Return that to the caller.
This is fairly general description that will hold for most older hash functions. Some details might be slightly wrong (subtly different padding scheme, whether or not to include a block of empty padding on
digest()invocations, etc.).The details aren’t super important. Just the rhythm of the design.
init()update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
- …
digest()
- load buffer, pad,
compress()- serialize internal state
- return
And thus, without having to know any of the details about what
compress()even looks like, the reason why length extension attacks were ever possible should leap out at you!
Art by Khia.
If it doesn’t, look closely at the difference between
update()anddigest().There are only two differences:
update()doesn’t pad before callingcompress()digest()returns the internal state thatcompress()always mutatesThe reason length-extension attacks are possible is that, for some hash functions, the output of
digest()is its full internal state.This means that you can run take an existing hash function and pretend it’s the internal state after an
update()call instead of adigest()call by appending the padding and then, after callingcompress(), appending additional data of your choice.The (F)Utility of Length Extension
Length-Extension Attacks are mostly used for attacking naive message authentication systems where someone attempts to authenticate a message (M) with a secret key (k), but they construct it like so:
auth_code = vulnerable_hash(k.append(M))
If this sounds like a very narrow use-case, that’s because it is. However, it still broke Flickr’s API once, and it’s a popular challenge for CTF competitions around the world.Consequently, length-extension attacks are sometimes thought to be vulnerabilities of the construction rather than a vulnerability of the hash function. For a Message Authentication Code construction, these are classified under canonicalization attacks.
After all, even though SHA-256 is vulnerable to length-extension, but you can’t actually exploit it unless someone is using it in a vulnerable fashion.
That being said, it’s often common to say that hash functions like SHA-256 and SHA-512 are prone to length-extension.
Ways to Avoid Length-Extension Attacks
Use HMAC. HMAC was designed to prevent these kinds of attacks.Alternatively, if you don’t have any cryptographic secrets, you can always do what bitcoin did: Hash your hash again.
return sha256(sha256(message))
Note: Don’t actually do that, it’s dangerous for other reasons. You also don’t want to take this to an extreme. If you iterate your hash too many times, you’ll reinvent PBKDF1 and its insecurity. Two is plenty.Or you can do something really trivial (which ultimately became another standard option in the SHA-2 family of hash functions):
Always start with a 512-bit hash and then truncate your output so the attacker never recovers the entire internal state of your hash in order to extend it.
That’s why you’ll sometimes see SHA-512/224 and SHA-512/256 in a list of recommendations. This isn’t saying “use one or the other”, that’s the (rather confusing) notation for a standardized SHA-512 truncation.
Note: This is actually what SHA-384 has done all along, and that’s one of the reasons why you see SHA-384 used more than SHA-512.
If you want to be extra fancy, you can also just use a different hash function that isn’t vulnerable to length extension, such as SHA-3 or BLAKE2.
Questions and Answers
Art by Khia.
Why isn’t BLAKE2 vulnerable to length extension attacks?
Quite simply: It sets a flag in the internal hash state before compressing the final buffer.If you try to deserialize this state then invoke
update(), you’ll get a different result than BLAKE2’scompress()produced duringdigest().For a secure hash function, a single bit of difference in the internal state should result in a wildly different output. (This is called the avalanche effect.)
Why isn’t SHA-3 vulnerable to length extension attacks?
SHA-3 is a sponge construction whose internal state is much larger than the hash function output. This prevents an attacker from recovering the hash function’s internal state from a message digest (similar to the truncated hash function discussed above).Why don’t length-extension attacks break digital signature algorithms?
Digital signature algorithms–such as RSASSA, ECDSA, and EdDSA–take a cryptographic hash of a message and then perform some asymmetric cryptographic transformation of the hash with the secret key to produce a signature that can be verified with a public key. (The exact details are particular to the signature algorithm in question.)Length-extension attacks only allow you to take a valid H(k || m) and produce a valid H(k || m || padding || extra) hash that will validate, even if you don’t know k. They don’t magically create collisions out of thin air.
Even if you use a weak hash function like SHA-1, knowing M and H(M) is not sufficient to calculate a valid signature. (You need to be able to know these values in order to verify the signature anyway.)
The security of digital signature algorithms depends entirely on the secrecy of the signing key and the security of the asymmetric cryptographic transformation used to generate a signature. (And its resilience to side-channel attacks.)
However, a more interesting class of attack is possible for systems that expect digital signatures to have similar properties as cryptographic hash functions. This would qualify as a protocol vulnerability, not a length-extension vulnerability.
TL;DR
Art by Khia.
Length-extension attacks exploit a neat property of a few cryptographic hash functions–most of which you shouldn’t be using in 2020 anyway (SHA-2 is still fine)–but can only be exploited by a narrow set of circumstances.
If you find yourself trying to use length-extension to break anything else, you’ve probably run into a cryptographic dead end and need to backtrack onto more interesting avenues of exploitation–of which there are assuredly many (unless your cryptography is boring).
Next: Timing Side-Channels
https://soatok.blog/2020/10/06/dead-ends-in-cryptanalysis-1-length-extension-attacks/
#cryptanalysis #crypto #cryptographicHashFunction #cryptography #lengthExtensionAttacks