Search
Items tagged with: FIPSCompliance
Let’s talk about digital signature algorithms.
Digital signature algorithms are one of the coolest ideas to come out of asymmetric (a.k.a. public-key) cryptography, but they’re so simple and straightforward that most cryptography nerds don’t spend a lot of time thinking about them.
Even though you are more likely to run into a digital signature as a building block (e.g. certificate signatures in TLS) than think about them in isolation (e.g. secure software releases), they’re still really cool and worth learning about.
What’s a Digital Signature?
A digital signature is some string that proves that a specific message was signed by some specific entity in possession of the secret half of an asymmetric key-pair. Digital Signature Algorithms define the process for securely signing and verifying messages with their associated signatures.
For example, if I have the following keypair:
- Secret key:
9080a2c7897faeb8526968161695da0f7b3afa2e8e7d8e8369a85547ab48ea05 - Public key:
482b8d3430445cdad6b5ce59778e09ab59d099120f32d316e881db1a6330390b
I can cryptographically sign the message “Dhole Moments: Never a dull moment!” with the above secret key, and it will generate the signature string: 63629779a31b623486145359c6f1d56602d8d9135e4b17fa2ae3667c8947397decd7ae01bfed08645a429f5dee906e87df4e18eefdfff9acb5b1488c9dec800f.
If you only have the message, signature string, and my public key, you can verify that I signed the message. But, very crucially, you cannot sign messages and convince someone else that they came from me. (With symmetric authentication schemes, such as HMAC, you can.)
A digital signature algorithm is considered secure if, in order for anyone else to pass off a different message as being signed by me, they would need my secret key to succeed. When this assumption holds true, we say the scheme is secure against existential forgery attacks.
How Do Digital Signatures Work?
Simple answer: They generally combine a cryptographic hash function (e.g. SHA-256) with some asymmetric operation, and the details beyond that are all magic.
More complicated answer: That depends entirely on the algorithm in question!

For example, with RSA signatures, you actually encrypt a hash of the message with your secret key to sign the message, and then you RSA-decrypt it with your public key to verify the signature. This is backwards from RSA encryption (where you do the totally sane thing: encrypt with public key, decrypt with secret key).
In contrast, with ECDSA signatures, you’re doing point arithmetic over an elliptic curve (with a per-signature random value).
Yet another class of digital signature algorithms are hash-based signatures, such as SPHINCS+ from the NIST Post-Quantum Cryptography Standardization effort, wherein your internals consist entirely of hash functions (and trees of hash functions, and stream ciphers built with other hash functions).
In all cases, the fundamental principle stays the same: You sign a message with a secret key, and can verify it with a public key.
In the interest of time, I’m not going to dive deep into how each signature algorithm works. That can be the subject of future blog posts (one for each of the algorithms in question).
Quick aside: Cryptographers who stumble across my blog might notice that I deviate from convention a bit. They typically refer to the sensitive half of an asymmetric key pair as a “private key”, but I instead call it a “secret key”.
The main reason for this is that “secret key” can be abbreviated as “sk” and public key can be abbreviated as “pk”, whereas private/public doesn’t share this convenience. If you ever come across their writings and wonder about this discrepancy, I’m breaking away from the norm and their way is more in line with the orthodoxy.
What Algorithms Should I Use?

If you find yourself asking this question, you’re probably dangerously close to rolling your own crypto. If so, you’ll want to hire a cryptographer to make sure your designs aren’t insecure. (It’s extremely easy to design or implement otherwise-secure cryptography in an insecure way.)
Recommended Digital Signature Algorithms
(Update, 2022-05-19): I’ve published a more in-depth treatment of the Elliptic Curve Digital Signature Algorithms a few years after this post was created. A lot of the topics covered by EdDSA and ECDSA are focused on there.
EdDSA: Edwards Curve DSA
EdDSA comes in two variants: Ed25519 (widely supported in a lot of libraries and protocols) and Ed448 (higher security level, but not implemented or supported in as many places).
The IETF standardized EdDSA in RFC 8032, in an effort related to the standardization of RFC 7748 (titled: Elliptic Curves for Security).
Formally, EdDSA is derived from Schnorr signatures and defined over Edwards curves. EdDSA’s design was motivated by the real-world security failures of ECDSA:
- Whereas ECDSA requires a per-signature secret number (
) to protect the secret key, EdDSA derives the per-signature nonce deterministically from a hash of the secret key and message.
- ECDSA with biased nonces can also leak your secret key through lattice attacks. To side-step this, EdDSA uses a hash function twice the size as the prime (i.e. SHA-512 for Ed25519), which guarantees that the distribution of the output of the modular reduction is unbiased (assuming uniform random inputs).
- ECDSA implemented over the NIST Curves is difficult to implement in constant-time: Complicated point arithmetic rules, point division, etc. EdDSA only uses operations that are easy to implement in constant-time.
For a real-world example of why EdDSA is better than ECDSA, look no further than the Minerva attacks, and the Ed25519 designer’s notes on why EdDSA stood up to the attacks.
The security benefits of EdDSA over ECDSA are so vast that FIPS 186-5 is going to include Ed25519 and Ed448.

This is kind of a big deal! The FIPS standards are notoriously slow-moving, and they’re deeply committed to a sunk cost fallacy on algorithms they previously deemed acceptable for real-world deployment.
RFC 6979: Deterministic ECDSA
Despite EdDSA being superior to ECDSA in virtually every way (performance, security, misuse-resistance), a lot of systems still require ECDSA support for the foreseeable future.
If ECDSA is here to stay, we might as well make it suck less in real-world deployments. And that’s exactly what Thomas Pornin did when he wrote RFC 6979: Deterministic Usage of DSA and ECDSA.
(Like EdDSA, Deterministic ECDSA is on its way to FIPS 186-5. Look for it in FIPS-compliant hardware 5 years from now when people actually bother to update their implementations.)
Acceptable Digital Signature Algorithms
ECDSA Signatures
The Elliptic Curve Digital Signature Algorithm (ECDSA) is the incumbent design for signatures. Unlike EdDSA, ECDSA is a more flexible design that has been applied to many different types of curves.
This is more of a curse than a blessing, as Microsoft discovered with CVE-2020-0601: You could take an existing (signature, public key) pair with standard curve, explicitly set the generator point equal to the victim’s public key, and set your secret key to 1, and Windows’s cryptography library would think, “This is fine.”
For this reason, cryptographers were generally wary of proposals to add support for Koblitz curves (including secp256k1–the Bitcoin curve) or Brainpool curves into protocols that are totally fine with NIST P-256 (and maybe NIST P-384 if you need it for compliance reasons).
For that reason, if you can’t use EdDSA or RFC 6979, your fallback option is ECDSA with one of those two curves (secp256r1, secp384r1), and making sure that you have access to a reliable cryptographic random number generator.
RSA Signatures
It’s high time the world stopped using RSA.
Not just for the reasons that Trail of Bits is arguing (which I happen to agree with), but more importantly:
Replacing RSA with EdDSA (or Deterministic ECDSA) also gives teams an opportunity to practice migrating from one cryptography algorithm suite to another, which will probably be a much-needed experience when quantum computers come along and we’re all forced to migrate to post-quantum cryptography.
Encryption is a bigger risk of being broken by quantum computers than signature schemes: If you encrypt data today, a quantum computer 20 years down the line can decrypt it immediately. Conversely, messages that are signed today cannot be broken until after a quantum computer exists.
That being said, if you only need signatures and not encryption, RSA is still acceptable. If you also need encryption, don’t use RSA for that purpose.
If you can, use PSS padding rather than PKCS#1 v1.5 padding, with SHA-256 or SHA-384. But for signatures (i.e. not encryption), PKCS#1 v1.5 padding is fine.
Dishonorable Mention
DSA Signatures
There’s really no point in using classical DSA, when ECDSA is widely supported and has more ongoing attention from cryptography experts.
If you’re designing a system in 2020 that uses DSA, my only question for you is…

Upcoming Signature Algorithms
Although it is far too early to consider adopting these yet, cryptographers are working on new designs that protect against wider ranges of real-world threats.
Let’s briefly look at some of them and speculate wildly about what the future looks like. For fun. Don’t use these yet, unless you have a very good reason to do so.
Digital Signature Research Topics
Hedged Signatures
Above, we concluded that EdDSA and Deterministic ECDSA were generally the best choice (and what I’d recommend for software developers). There is one important caveat: Fault attacks.
A fault attack is when you induce a hardware fault into a computer chip, and thereby interfere with the correct functioning of a cryptography algorithm. This is especially relevant to embedded devices and IoT.
The IETF’s CFRG is investigating the use of additional randomization of messages (rather than randomizing signatures) as a safeguard against leaking secret keys through fault injection.
Of course, the Dhole Cryptography Library (my libsodium wrapper for JavaScript and PHP) already provides a form of Hedged Signatures.
If this technique is proven successful at mitigating fault injection attacks, then libsodium users will be able to follow the technique outlined in Dhole Crypto to safeguard their own protocols against fault attacks. Until then, they’re at least as safe as deterministic EdDSA today.
Threshold ECDSA Signatures
Suppose you have a scenario where you want 3-or-more people to have to sign a message before it’s valid. That’s exactly what Threshold ECDSA with Fast Trustless Setup aspires to provide.
Although this is mostly being implemented in cryptocurrency projects today, the cryptography underpinnings are fascinating. At worst, this will be one good side-effect to come from blockchain mania.
Post-Quantum Digital Signatures
Hash-Based Signatures
The best hash-based signature schemes are based on the SPHINCS design for one simple reason: It’s stateless.
In earlier hash-based digital signatures, such as XMSS, you have to maintain a state of which keys you’ve already used, to prevent attacks. Google’s Adam Langley previously described this as a “huge foot-cannon” for security (although probably okay in some environments, such as an HSM).
Lattice-Based Signatures
There are a lot of post-quantum signature algorithm designs defined over lattice groups, but my favorite lattice-based design is called FALCON. FALCON stands for FAst-Fourier Lattice-based COmpact Signatures Over NTRU.
Sign Here, Please
Who knew there would be so much complexity involved with such a simple cryptographic operation? And we didn’t even dive deep on how any of them work.
That’s the problem with cryptography: It’s a fractal of complexity. The more you know about these topics, the deeper the complexity becomes.
But if you’re implementing a protocol today and need a digital signature algorithm, use (in order of preference):
- Ed25519 or Ed448
- ECDSA over NIST P-256 or P-384, with RFC 6979
- ECDSA over NIST P-256 or P-384, without RFC 6979
- RSA (as a last resort)
But most importantly: make sure you have a cryptographer audit your designs.
(Header art by Kyume.)
https://soatok.blog/2020/04/26/a-furrys-guide-to-digital-signature-algorithms/
#crypto #cryptography #DeterministicSignatures #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #FIPS #FIPS186 #FIPSCompliance #RFC6979 #SecurityGuidance
Earlier this year, Cendyne published A Deep Dive into Ed25519 Signatures, which covered some of the different types of digital signature algorithms, but mostly delved into the Ed25519 algorithm. Truth in advertising.This got me thinking, “Why isn’t there a better comparison of different elliptic curve signature algorithms available online?”
Art: LvJ
Most people just defer to SafeCurves, but it’s a little dated: We have complete addition formulas for Weierstrass curves now, but SafeCurves doesn’t reflect that.
For the purpose of simplicity, I’m not going to focus on a general treatment of Elliptic Curve Cryptography (ECC), which includes pairing-based cryptography, Elliptic-Curve Diffie-Hellman, and (arguably) isogeny cryptography.
Instead, I’m going to focus entirely on elliptic curve digital signature algorithms.
Note: The content of this post is a bit lower-level than most programmers ever need to be concerned with. If you’re a programmer and interested in learning cryptography, start here. If you’re looking for library recommendations, libsodium is a good safe default.
Compliance Rules Everything Around Me
If you have to meet some arbitrary compliance requirements (i.e. FIPS 140-3, CNSA, etc.), your decision is already made for you, and you shouldn’t waste your time reading blogs like this that will only get your hopes up about the options available to you.Choose the option your compliance officer demands, and hope it’s good enough.
“Sure, let me check that box.”
Art: LvJElliptic Curves for Signature Algorithms
Let’s start with the same curve Cendyne analyzed: Ed25519.Ed25519 (EdDSA, Curve25519)
Ed25519 is one of the two digital signature algorithms today that use the EdDSA algorithm framework. The other is Ed448, which targets a higher security level (224-bit vs 128-bit) but is also slower and uses SHAKE256 (which is overkill and not great for performance).Ed25519 is a safe default choice for most applications where a digital signature is appropriate, for many reasons:
- Ed25519 uses deterministic nonces, which means you’re severely unlikely to ever reproduce the Sony ECDSA k-reuse bug in your system.
The deterministic nonce is calculated from the SHA512 hash of the secret key and message. Two invocations tocrypto_sign_ed25519()with the same message and secret key will produce the same signature, but the intermediate nonce value is never revealed to an attacker.- Ed25519 includes the public key in the data hashed to produce the signature (more specifically s from the (R,s) pair). This offers a property that ECDSA lacks: Exclusive Ownership. I’ve written about this property before.
Without Exclusive Ownership, it’s possible to create a single signature value that’s valid for multiple different (message, public key) pairs.Years ago, there would have an additional list item: Ed25519 uses Edward Curves, which have complete addition formulas and are therefore safer to implement in constant-time than Weierstrass curves (i.e. the NIST curves). However, we now have complete addition formulas for Weierstrass curves, so this has become a moot point (assuming your implementation uses complete addition formulas).
Ed25519 targets the 128-bit security level.
Why Not Use Ed25519?
There is one minor pitfall of Ed25519 that makes it unsuitable for esoteric uses (say, Ring Signature Schemes or zero-knowledge proofs): Ed25519 is not a prime-order group; it has a cofactor h = 8. This detail famously created a double-spend vulnerability in all CryptoNote-based cryptocurrencies (including Monero).For systems that want the security of Ed25519 and its various well-studied implementations, but still need a prime-order group for their protocol, cryptographers have developed the Ristretto Group to meet your needs.
If you’re working on embedded systems, the determinism inherent to EdDSA might be undesirable due to the possibility of fault attacks. You can use a hedged variant of Ed25519 to mitigate this risk.
Additionally, Ed25519 is not approved for many government applications, although it did make the latest draft revision of FIPS 186 in 2019. If you care about compliance (see above), you cannot use Ed25519. Yet.
A niche Internet meme for cryptography engineers
Guidance for Ed25519
Unless legally prohibited, Ed25519 should be your default choice, unless you need a prime-order group. In that case, build your desired protocol atop Ristretto255.If you’re not sure if you need a prime-order group, you probably don’t. It’s a specialized requirement for uncommon use cases (ring signatures, password authenticated key exchange protocols, zero-knowledge proofs, etc.).
Art: LvJ
The Bitcoin Curve (ECDSA, secp256k1)
Secp256k1 is a Koblitz curve, which is a special case of Weierstrass curves that are more performant when used in binary fields, of the form,. This curve is almost exclusively used in cryptocurrency software.
There is no specified reason why Bitcoin chose secp256k1 over another elliptic curve at the time of its inception, but we can speculate:
The author was a pseudonymous contributor to the Metzdowd mailing list for cypherpunks, and probably didn’t trust the NIST curves. Since Ed25519 didn’t exist at the time, the only obvious choice for a hipster elliptic curve parameter selection was to rely on the SECG recommendations, which specify the NIST and Koblitz curves. If you cross the NIST curves off the list, only the Koblitz curves remained.
Therefore, the selection of secp256k1 is likely an artefact of computer history and not a compelling reason to select secp256k1 in new designs. Please look elsewhere.
Fact: Imgflip didn’t have a single secp256k1 meme until I made this one.
Secp256k1 targets the 128-bit security level.
Guidance for secp256k1
Don’t bother, there are better options. (i.e. Ed25519)If you’re writing software for a cryptocurrency-related project, and you feel compelled to use secp256k1 for the sake of reducing your code footprint, please strongly consider the option of burning everything to the proverbial ground.
Cryptocurrency sucks!
Art: SwizzCryptocurrency Aside, Why Avoid Secp256k1?
As we noted above, secp256k1 isn’t widely used outside of cryptocurrency.As a direct consequence of this (as we’ll discuss in the NIST P-256 section), most cryptography libraries don’t offer optimized, side-channel-resistant implementations of secp256k1; even if they do offer optimized implementations of NIST P-256.
(Meanwhile, Ed25519 is designed to be side-channel and misuse-resistant, partly due to its Schnorr construction and constant-time ladder for scalar multiplication, so any library that implements Ed25519 is overwhelmingly likely to be constant-time.)
Therefore, any secp256k1 library for most programming languages that isn’t an FFI wrapper for libsecp256k1 will have worse performance than the other 256-bit curves.
https://twitter.com/bascule/status/1320183684935290882
Additionally, secp256k1 implementations are often a source of exploitable side-channels that permit attackers to pilfer your secret keys.
The previously linked article was about BouncyCastle’s implementation (which covers Java and .NET), but there’s still plenty of secp256k1 implementations that don’t FFI libsecp256k1.
From a quick Google Search:
- Python (uses EEA rather than Binary GCD for modular inverse)
- Go (uses Numbers, which weren’t designed for cryptography)
- PHP (uses GMP, which isn’t constant-time)
- JavaScript (calls here, which uses bn.js, which isn’t constant-time)
If you’re using secp256k1, and you’re not basing your choice on cybercash-interop, you’re playing with fire at the implementation and ecosystem levels–even if there are no security problems with the Koblitz curve itself.
You are much better off choosing any different curve than secp256k1 if you don’t have a Bitcoin/Ethereum/etc. interoperability requirement.
“No thanks, I use Ed25519.”
Art: LvJNIST P-256 (ECDSA, secp256r1)
NIST P-256 is the go-to curve to use with ECDSA in the modern era. Unlike Ed25519, P-256 uses a prime-order group, and is an approved algorithm to use in FIPS-validated modules.Most cryptography libraries offer optimized assembly implementations of NIST P-256, which makes it less likely that your signing operations will leak timing information or become a significant performance bottleneck.
P-256 targets the 128-bit security level.
Why Not Use P-256?
Once upon a time, P-256 was riskier than Ed25519 (for signatures) and X25519 (for Diffie-Hellman), due to the incomplete addition formulas that led to timing-leaky implementations.If you’re running old software, you may still be vulnerable to timing attacks that can recover your ECDSA secret key. However, there is a good chance that you’re on a modern and secure implementation in 2022, especially if you’re outsourcing this to OpenSSL or its derivatives.
ECDSA requires a secure randomness source to sign data. If you don’t have one available, and you sign anything, you’re coughing up your secret key to any attacker capable of observing multiple signatures.
Guidance for P-256
P-256 is an acceptable choice, especially if you’re forced to cope with FIPS and/or the CNSA suite requirements when using cryptography.Of course, if you can get away with Ed25519, use Ed25519 instead.
If you use P-256, make sure you’re using it with SHA-256. Some implementations may default to something weaker (e.g. SHA-1).
If you’re also going to be performing ECDH with P-256, make sure you use compressed points. There used to be a patent; it died in 2018.
If you can afford it, make sure you use deterministic ECDSA (RFC 6979) or hedged signatures (if fault attacks are relevant to your threat model).
Art: LvJ
NIST P-384 (ECDSA, secp384r1)
NIST P-384 has a larger field than the curves we’ve previously examined, which allows P-384 to target the 192-bit security level. That’s the primary reason why anyone would choose P-384.Naturally, elliptic curve security is more complicated than merely security against the Elliptic Curve Discrete Logarithm Problem (ECDLP).
P-384 is most often paired with SHA-384, which is the most widely used flavor of the SHA-2 family hash functions that isn’t susceptible to length-extension attacks. (There are also truncated SHA-512 variants specified later, but that’s also what SHA-384 is under-the-hood.)
If you’re aiming to build a “secure-by-default” tool for a system that the US government might one day become a customer of, with minimal cryptographic primitive choice, using NIST P-384 with SHA-384 makes for a reasonably minimalistic bundle.
Why Not Use P-384?
Unlike P-256, most P-384 implementations don’t use constant-time, optimized, and/or formally verified assembly code. (Notable counter-examples: AWS-LC and Go x/crypto.)Like P-256, P-384 also requires a secure randomness source to sign data. If you aren’t providing one, expect your signing key to end up on fail0verflow one day.
Guidance for P-384
If you use P-384, make sure you’re using it with SHA-384.The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.
Art: Kyume
NIST P-521 (ECDSA, secp521r1)
Biggest curve is best curve! — the cluelesshttps://www.youtube.com/watch?v=i_APoSfCYwU
Systems that choose P-521 often have an interesting threat model, even though said threat model is rarely formally specified.
It’s overwhelmingly likely that what eventually breaks the 256-bit elliptic curves will also break P-521 in short order: Cryptography Relevant Quantum Computers.
The only thing P-521 does against CRQCs that P-256 doesn’t is require more quantum memory. If you’re worried about QRQCs, you might want to look into hybrid post-quantum signature schemes.
If you’re choosing P-521 in your designs, you’re basically saying, “I want to have 256 bits of asymmetric cryptographic security, come hell or high water!” even though the 128-bit security level is likely just fine for your actual threats.
Aside: P-521 and 512-bit ECC Security
P-521 is not a typo, although people sometimes think it is. P-521 uses the Mersenne primeinstead of a 512-bit near-Mersenne prime.
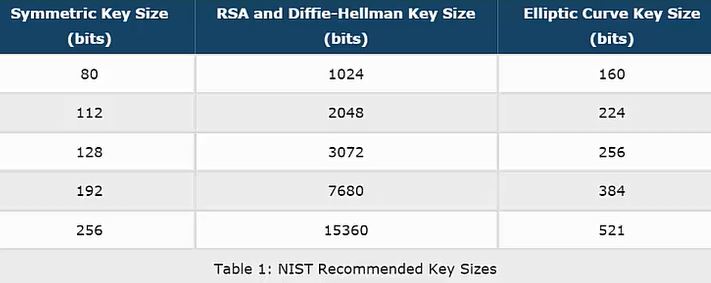
This has led to an unfortunate trend in cryptography media to map ECC key sizes to symmetric security levels that misleads people as to the relationship between the two. For example:
Regrettably, this is misleading, because plotting the ECC Key Size versus equivalent Symmetric Security isn’t a how ECDLP security works. The ratio of the exponents involved is totally linear; it doesn’t suddenly increase beyond 384-bit curves for a mysterious mathematical reason.
- 256-bit Curves target the 128-bit security level
- 384-bit Curves target the 192-bit security level
- 512-bit Curves target the 256-bit security level
- 521-bit Curves actually target the 260-bit security level, but that meets or exceeds the 256-bit security level, so that’s how the standards are interpreted
The reason for this boils down entirely to the best attack against the Elliptic Curve Discrete Logarithm Problem: Pollard’s Rho, which recovers the secret key from an
-bit public key (which has a
search space) in
guesses.
Taking the square root of a number is the same as halving its exponent, so the security level is half:
.
Takeaway: If someone tells you that you need a 521-bit curve to meet the 256-bit security level, they are mistaken and it’s not their fault.
Art: Harubaki
Why Not Use P-521?
It’s slow. Much slower than P-256 and Ed25519. Modestly slower than P-384.Unlike P-384, you’re less likely to find an optimized, constant-time P-521 implementation.
Guidance for P-521
First, make a concerted effort to figure out the motivation for P-521 in your designs. Chances are, someone is putting too much emphasis on the wrong things for security.If you use P-521, make sure you’re using it with SHA-512.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.
Art: LvJ
Ed448 (EdDSA, Curve448)
Ed448 is the P-521 of the Edwards curves: It mostly exists to give standards committees a psychological comfort for the unlikely event that 256-bit ECC is desperately broken but ECC larger than 384 bits is somehow still safe.https://twitter.com/dchest/status/703017144053833728
The very concept of having multiple “security levels” for raw cryptography primitives is mostly an artefact of the historical military roots of cryptography, rather than a serious consideration in the modern world.
Unfortunately, this leads to implementations that prioritize runtime algorithm selection negotiation, which maximizes the risk of protocol-level vulnerabilities. See also: JWT.
Ed448 was specified to use SHAKE256, which is a needlessly conservative decision which leads to an unnecessary performance bottleneck.
Why Not Use Ed448?
Aside from the performance hit mentioned previously, there’s no compelling reason to avoid Ed448 that isn’t also true of either Ed25519 or P-384.Guidance for Ed448
If you want more speed, go with Ed25519. In addition to being faster, Ed25519 is also very widely supported.If you need a prime-order field, use Decaf with Ed448 or consider P-384.
The Brainpool Curves
The main motivation for the Brainpool curves is that the NIST curves were not generated in a “verifiable pseudo-random way”.The only reasons you’d ever want to support the Brainpool curves include:
- You think the NIST curves are somehow backdoored by the NSA
- You don’t appreciate small attack surfaces in cryptography libraries
- The German government told you to (see: compliance)
Most of the advice for the NIST Curves at each security level can be copy/pasted for the Brainpool curves, with one important caveat:
When considering real-world implementations, Brainpool curves are more likely to use the general purpose Big Number procedures (which aren’t always constant-time), rather than optimized assembly code, than the NIST curves are.
Therefore, my general guidance for the Brainpool curves is simply:
- Proceed at your own peril
- Consider hiring a cryptography engineer to study the implementation you’re relying on, especially with regard to timing attacks
Me when I hear “brainpool”
Art: LvJRe-Examining the SafeCurves Criteria
Here’s a 2022 refresh of the SafeCurves criteria for all of the curves considered by this blog post.
SafeCurve Criteria Relevance to the Curves Listed Above Fields All relevant curves satisfy the requirements Equations All relevant curves satisfy the requirements Base Points All relevant curves satisfy the requirements Rho All relevant curves satisfy the requirements Transfers All relevant curves satisfy the requirements Discriminants Only secp256k1 doesn’t satisfy the requirements (out of the curves listed in this blog post) Rigidity The NIST curves do not meet this requirement.
If you care about whether or not the standards were manipulated to insert a backdoor, rigidity matters to you. Otherwise, it’s not a deal-breaker.Ladders While a Montgomery ladder is beneficial for speed and implementation security, it isn’t strictly speaking required.
This is an icing-on-the-cake consideration.Twists The only curve listed above that doesn’t meet the requirement is the 256-bit Brainpool curve (brainpoolp256t1). Completeness All relevant curves satisfy the requirements, as of 2015.
SafeCurves is out of date here.Indistinguishability All relevant curves satisfy the requirements, as of 2014. SafeCurves continues to be a useful resource, especially if you stray from the guidance on this page.
For example: You wouldn’t want to use pairing-friendly curves for general purpose ECC digital signatures, because they’re suitable for specialized problems. SafeCurves correctly recommends not using BN(2,254).
However, SafeCurves is showing its age in 2022. BN curves still end up in digital signature protocol standards even though BLS-12-381 is clearly a better choice.
The Internet would benefit greatly for an updated SafeCurves that focuses on newer elliptic curve algorithms.
Art: Scruff
TL;DR
Ed25519 is great. NIST P-256 and P-384 are okay (with caveats). Anything else is questionable, and their parameter selection should come with a clear justification.https://soatok.blog/2022/05/19/guidance-for-choosing-an-elliptic-curve-signature-algorithm-in-2022/
#asymmetricCryptography #BrainpoolCurves #cryptography #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #ellipticCurveCryptography #P256 #P384 #P521 #secp256k1 #secp256r1 #secp384r1 #secp521r1 #SecurityGuidance