Search
Items tagged with: asymmetricCryptography
There is, at the time of this writing, an ongoing debate in the Crypto Research Forum Group (CFRG) at the IETF about KEM combiners.
One of the participants, Deirdre Connolly, wrote a blog post titled How to Hold KEMs. The subtitle is refreshingly honest: “A living document on how to juggle these damned things.”
Deirdre also co-authored the paper describing a Hybrid KEM called X-Wing, which combines X25519 with ML-KEM-768 (which is the name for a standardized tweak of Kyber, which I happened to opine on a few years ago).
After sharing a link to Deirdre’s blog in a few places, several friendly folk expressed confusion about KEMs in general.
So very briefly, here’s an introduction to Key Encapsulation Mechanisms in general, to serve as a supplementary resource for any future discussion on KEMs.
You shouldn’t need to understand lattices or number theory, or even how to read a mathematics paper, to understand this stuff.
Building Intuition for KEMs
For the moment, let’s suspend most real-world security risks and focus on a simplified, ideal setting.
To begin with, you need some kind of Asymmetric Encryption.
Asymmetric Encryption means, “Encrypt some data with a Public Key, then Decrypt the ciphertext with a Secret Key.” You don’t need to know, or even care, about how it works at the moment.
Your mental model for asymmetric encryption and decryption should look like this:
interface AsymmetricEncryption { encrypt(publicKey: CryptoKey, plaintext: Uint8Array); decrypt(secretKey: CryptoKey, ciphertext: Uint8Array);}
As I’ve written previously, you never want to actually use asymmetric encryption directly.
Using asymmetric encryption safely means using it to exchange a key used for symmetric data encryption, like so:
// Alice sends an encrypted key to BobsymmetricKey = randomBytes(32)sendToBob = AsymmetricEncryption.encrypt( bobPublicKey, symmetricKey)// Bob decrypts the encrypted key from Alicedecrypted = AsymmetricEncryption.decrypt( bobSecretKey, sendToBob)assert(decrypted == symmetricKey) // true
You can then use symmetricKey to encrypt your actual messages and, unless something else goes wrong, only the other party can read them. Hooray!
And, ideally, this is where the story would end. Asymmetric encryption is cool. Don’t look at the scroll bar.
Unfortunately
The real world isn’t as nice as our previous imagination.
We just kind of hand-waved that asymmetric encryption is a thing that happens, without further examination. It turns out, you have to examine further in order to be secure.
The most common asymmetric encryption algorithm deployed on the Internet as of February 2024 is called RSA. It involves Number Theory. You can learn all about it from other articles if you’re curious. I’m only going to describe the essential facts here.
Keep in mind, the primary motivation for KEMs comes from post-quantum cryptography, not RSA.
From Textbook RSA to Real World RSA
RSA is what we call a “trapdoor permutation”: It’s easy to compute encryption (one way), but decrypting is only easy if you have the correct secret key (the other way).
RSA operates on large blocks, related to the size of the public key. For example: 2048-bit RSA public keys operate on 2048-bit messages.
Encrypting with RSA involves exponents. The base of these exponents is your message. The outcome of the exponent operation is reduced, using the modulus operator, by the public key.
(The correct terminology is actually slightly different, but we’re aiming for intuition, not technical precision. Your public key is both the large modulus and exponent used for encryption. Don’t worry about it for the moment.)
If you have a very short message, and a tiny exponent (say, 3), you don’t need the secret key to decrypt it. You can just take the cube-root of the ciphertext and recover the message!
That’s obviously not very good!
To prevent this very trivial weakness, cryptographers proposed standardized padding schemes to ensure that the output of the exponentiation is always larger than the public key. (We say, “it must wrap the modulus”.)
The most common padding mode is called PKCS#1 v1.5 padding. Almost everything that implements RSA uses this padding scheme. It’s also been publicly known to be insecure since 1998.
The other padding mode, which you should be using (if you even use RSA at all) is called OAEP. However, even OAEP isn’t fool proof: If you don’t implement it in constant-time, your application will be vulnerable to a slightly different attack.
This Padding Stinks; Can We Dispense Of It?
It turns out, yes, we can. Safely, too!
We need to change our relationship with our asymmetric encryption primitive.
Instead of encrypting the secret we actually want to use, let’s just encrypt some very large random value.
Then we can use the result with a Key Derivation Function (which you can think of, for the moment, like a hash function) to derive a symmetric encryption key.
class OversimplifiedKEM { function encaps(pk: CryptoKey) { let N = pk.getModulus() let r = randomNumber(1, N-1) let c = AsymmetricEncryption.encrypt(pk, r) return [c, kdf(r)] } function decaps(sk: CryptoKey, c: Uint8Array) { let r2 = AsymmetricEncryption.decrypt(sk, c) return kdf(r2) }}
In the pseudocode above, the actual asymmetric encryption primitive doesn’t involve any sort of padding mode. It’s textbook RSA, or equivalent.
KEMs are generally constructed somewhat like this, but they’re all different in their own special, nuanced ways. Some will look like what I sketched out, others will look subtly different.Understanding that KEMs are a construction on top of asymmetric encryption is critical to understanding them.
It’s just a slight departure from asymmetric encryption as most developers intuit it.
Cool, we’re almost there.
The one thing to keep in mind: While this transition from Asymmetric Encryption (also known as “Public Key Encryption”) to a Key Encapsulation Mechanism is easy to follow, the story isn’t as simple as “it lets you skip padding”. That’s an RSA specific implementation detail for this specific path into KEMs.
The main thing you get out of KEMs is called IND-CCA security, even when the underlying Public Key Encryption mechanism doesn’t offer that property.
IND-CCA security is a formal notion that basically means “protection against an attacker that can alter ciphertexts and study the system’s response, and then learn something useful from that response”.
IND-CCA is short for “indistinguishability under chosen ciphertext attack”. There are several levels of IND-CCA security (1, 2, and 3). Most modern systems aim for IND-CCA2.
Most people reading this don’t have to know or even care what this means; it will not be on the final exam. But cryptographers and their adversaries do care about this.
What Are You Feeding That Thing?
Deirdre’s blog post touched on a bunch of formal security properties for KEMs, which have names like X-BIND-K-PK or X-BIND-CT-PK.
Most of this has to deal with, “What exactly gets hashed in the KEM construction at the KDF step?” (although some properties can hold even without being included; it gets complicated).
For example, from the pseudocode in the previous section, it’s more secure to not only hash r, but also c and pk, and any other relevant transcript data.
class BetterKEM { function encaps(pk: CryptoKey) { let N = pk.getModulus() let r = randomNumber(1, N-1) let c = AsymmetricEncryption.encrypt(pk, r) return [c, kdf(pk, c, r)] } function decaps(sk: CryptoKey, c: Uint8Array) { let pk = sk.getPublickey() let r2 = AsymmetricEncryption.decrypt(sk, c) return kdf(pk, c, r2) }}
In this example, BetterKem is greatly more secure than OversimplifiedKEM, for reasons that have nothing to do with the underlying asymmetric primitive. The thing it does better is commit more of its context into the KDF step, which means that there’s less pliability given to attackers while still targeting the same KDF output.
If you think about KDFs like you do hash functions (which they’re usually built with), changing any of the values in the transcript will trigger the avalanche effect: The resulting calculation, which is not directly transmitted, is practically indistinguishable from random bytes. This is annoying to try to attack–even with collision attack strategies (birthday collision, Pollard’s rho, etc.).
However, if your hash function is very slow (i.e., SHA3-256), you might be worried about the extra computation and energy expenditure, especially if you’re working with larger keys.
Specifically, the size of keys you get from ML-KEM or other lattice-based cryptography.
That’s where X-Wing is actually very clever: It combines X25519 and ML-KEM-768 in such a way that binds the output to both keys without requiring the additional bytes of ML-KEM-768 ciphertext or public key.

However, it’s only secure to use it this way because of the specific properties of ML-KEM and X25519.
Some questions may come to mind:
- Does this additional performance hit actually matter, though?
- Would a general purpose KEM combiner be better than one that’s specially tailored to the primitives it uses?
- Is it secure to simply concatenate the output of multiple asymmetric operations to feed into a single KDF, or should a more specialized KDF be defined for this purpose?
Well, that’s exactly what the CFRG is debating!
Closing Thoughts
KEMs aren’t nearly as arcane or unapproachable as you may suspect. You don’t really even need to know any of the mathematics to understand them, though it certainly does help.
I hope that others find this useful.
Header art by Harubaki and AJ.
https://soatok.blog/2024/02/26/kem-trails-understanding-key-encapsulation-mechanisms/
#asymmetricCryptography #cryptography #KDF #KEM #keyEncapsulationMechanism #postQuantumCryptography #RSA
Did you know that, in the Furry Fandom, the most popular choice in species for one’s fursona is actually a hybrid?
Source: FurScience
Of course, we’re not talking about that kind of hybrid today. I just thought it was an amusing coincidence.
Art: Lynx vs Jackalope
Nor are we talking about what comes to mind for engineers accustomed to classical cryptography when you say Hybrid.
(Such engineers typically envision some combination of asymmetric key encapsulation with symmetric encryption; because too many people encrypt with RSA directly and the sane approach is often described as a Hybrid Cryptosystem in the literature.)
Rather, Hybrid Cryptography in today’s context refers to:
Cryptography systems that use a post-quantum cryptography algorithm, combined with one of the algorithms deployed today that aren’t resistant to quantum computers.
If you need to differentiate the two, PQ-Hybrid might be a better designation.Why Hybrid Cryptosystems?
At some point in the future (years or decades from now), humanity may build a practical quantum computer. This will be a complete disaster for all of the cryptography deployed on the Internet today.In response to this distant existential threat, cryptographers have been hard at work designing and attacking algorithms that remain secure even when quantum computers arrive. These algorithms are classified as post-quantum cryptography (mostly to distinguish it from techniques that uses quantum computers to facilitate cryptography rather than attack it, which is “quantum cryptography” and not really worth our time talking about). Post-quantum cryptography is often abbreviated as “PQ Crypto” or “PQC”.
However, a lot of the post-quantum cryptography designs are relatively new or comparatively less studied than their classical (pre-quantum) counterparts. Several of the Round 1 candidates to NIST’s post quantum cryptography project were broken immediately (PDF). Exploit code referenced in PDF duplicated below.:
#!/usr/bin/env python3import binascii, structdef recover_bit(ct, bit): assert bit < len(ct) // 4000 ts = [struct.unpack('BB', ct[i:i+2]) for i in range(4000*bit, 4000*(bit+1), 2)] xs, ys = [a for a, b in ts if b == 1], [a for a, b in ts if b == 2] return sum(xs) / len(xs) >= sum(ys) / len(ys)def decrypt(ct): res = sum(recover_bit(ct, b) << b for b in range(len(ct) // 4000)) return int.to_bytes(res, len(ct) // 4000 // 8, 'little')kat = 0for l in open('KAT_GuessAgain/GuessAgainEncryptKAT_2000.rsp'): if l.startswith('msg = '): # only used for verifying the recovered plaintext. msg = binascii.unhexlify(l[len('msg = '):].strip()) elif l.startswith('c = '): ct = binascii.unhexlify(l[len('c = '):].strip()) print('{}attacking known-answer test #{}'.format('\n' * (kat > 0), kat)) print('correct plaintext: {}'.format(binascii.hexlify(msg).decode())) plain = decrypt(ct) print('recovered plaintext: {} ({})'.format(binascii.hexlify(plain).decode(), plain == msg)) kat += 1
More pertinent to our discussions: Rainbow, which was one of the Round 3 Finalists for post-quantum digital signature algorithms, was discovered in 2020 to be much easier to attack than previously thought. Specifically, for the third round parameters, the attack cost was reduced by a factor of
,
, and
.
That security reduction is just a tad bit more concerning than a Round 1 candidate being totally broken, since NIST had concluded by then that Rainbow was a good signature algorithm until that attack was discovered. Maybe there are similar attacks just waiting to be found?
Given that new cryptography is accompanied by less confidence than incumbent cryptography, hybrid designs are an excellent way to mitigate the risk of attack advancements in post-quantum cryptography:
If the security of your system requires breaking the cryptography used today AND breaking one of the new-fangled designs, you’ll always be at least as secure as the stronger algorithm.
Art: Lynx vs Jackalope
Why Is Hybrid Cryptography Controversial?
Despite the risks of greenfield cryptographic algorithms, the NSA has begun recommending a strictly-PQ approach to cryptography and have explicitly stated that they will not require hybrid designs.Another pushback on hybrid cryptography comes from Uri Blumenthal of MIT’s Lincoln Labs on the IETF CFRG mailing list (the acronym CRQC expands to “Cryptographically-Relevant Quantum Computer”):
Here are the possibilities and their relation to the usefulness of the Hybrid approach.1. CRQC arrived, Classic hold against classic attacks, PQ algorithms hold – Hybrid is useless.
2. CRQC arrived, Classic hold against classic attacks, PQ algorithms fail – Hybrid is useless.
3. CRQC arrived, Classic broken against classic attacks, PQ algorithms hold – Hybrid is useless.
4. CRQC arrived, Classic hold against classic attacks, PQ algorithms broken – Hybrid useless.
5. CRQC doesn’t arrive, Classic hold against classic attacks, PQ algorithms hold – Hybrid is useless.
6. CRQC doesn’t arrive, Classic hold against classic attacks, PQ algorithms broken – Hybrid helps.
7. CRQC doesn’t arrive, Classic broken against classic attacks, PQ algorithms hold – Hybrid is useless.
8. CRQC doesn’t arrive, Classic broken against classic attacks, PQ algorithms broken – Hybrid is useless.
Uri Blumenthal, IETF CFRG mailing list, December 2021 (link)
Why Hybrid Is Actually A Damn Good Idea
Art: Scruff Kerfluff
Uri’s risk analysis is, of course, flawed. And I’m not the first to disagree with him.
First, Uri’s framing sort of implies that each of the 8 possible outputs of these 3 boolean variables are relatively equally likely outcomes.
It’s very tempting to look at this and think, “Wow, that’s a lot of work for something that only helps in 12.5% of possible outcomes!” Uri didn’t explicitly state this assumption, and he might not even believe that, but it is a cognitive trap that emerges in the structure of his argument, so watch your step.
Second, for many candidate algorithms, we’re already in scenario 6 that Uri outlined! It’s not some hypothetical future, it’s the present state of affairs.
To wit: The advances in cryptanalysis on Rainbow don’t totally break it in a practical sense, but they do reduce the security by a devastating margin (which will require significantly larger parameter sets and performance penalties to remedy).
For many post-quantum algorithms, we’re still uncertain about which scenario is most relevant. But since PQ algorithms are being successfully attacked and a quantum computer still hasn’t arrived, and classical algorithms are still holding up fine, it’s very clear that “hybrid helps” is the world we most likely inhabit today, and likely will for many years (until the existence of quantum computers is finally settled).
Finally, even in other scenarios (which are more relevant for other post-quantum algorithms), hybrid doesn’t significantly hurt security. It does carry a minor cost to bandwidth and performance, and it does mean having a larger codebase to review when compared with jettisoning the algorithms we use today, but I’d argue that the existing code is relatively low risk compared to new code.
From what I’ve read, the NSA didn’t make as strong an argument as Uri; they said hybrid would not be required, but didn’t go so far as to attack it.
Hybrid cryptography is a long-term bet that will protect the most users from cryptanalytic advancements, contrasted with strictly-PQ and no-PQ approaches.
Why The Hybrid Controversy Remains Unsettled
Even if we can all agree that hybrid is the way to go, there’s still significant disagreement on exactly how to do it.Hybrid KEMs
There are two schools of thought on hybrid Key Encapsulation Mechanisms (KEMs):
- Wrap the post-quantum KEM in the encrypted channel created by the classical KEM.
- Use both the post-quantum KEM and classical KEM as inputs to a secure KDF, then use a single encrypted channel secured by both.
The first option (layered) has the benefit of making migrations smoother. You can begin with classical cryptography (i.e. ECDHE for TLS ciphersuites), which is what most systems online support today. Then you can do your post-quantum cryptography inside the existing channel to create a post-quantum-secure channel. This also lends toward opportunistic upgrades (which might not be a good idea).
The second option (composite) has the benefit of making the security of your protocol all-or-nothing: You cannot attack the weak now and the strong part later. The session keys you’ll derive require attacking both algorithms in order to get access to the plaintext. Additionally, you only need a single layer. The complexity lies entirely within the handshake, instead of every packet.
Personally, I think composite is a better option for security than layered.
Hybrid Signatures
There are, additionally, two different schools of thought on hybrid digital signature algorithms. However, the difference is more subtle than with KEMs.
- Require separate classical signatures and post-quantum signatures.
- Specify a composite mode that combines the two together and treat it as a distinct algorithm.
To better illustrate what this looks like, I outlined what a composite hybrid digital signature algorithm could look like on the CFRG mailing list:
primary_seed := randombytes_buf(64) // store thised25519_seed := hash_sha512256(PREFIX_CLASSICAL || primary_seed)pq_seed := hash_sha512256(PREFIX_POSTQUANTUM || primary_seed)ed25519_keypair := crypto_sign_seed_keypair(ed25519_seed)pq_keypair := pqcrypto_sign_seed_keypair(pq_seed)
Your composite public key would be your Ed25519 public key, followed by your post-quantum public key. Since Ed25519 public keys are always 32 bytes, this is easy to implement securely.
Every composite signature would be an Ed25519 signature concatenated with the post-quantum signature. Since Ed25519 signatures are always 64 bytes, this leads to a predictable signature size relative to the post-quantum signature.
The main motivation for preferring a composite hybrid signature over a detached hybrid signature is to push the hybridization of cryptography lower in the stack so developers don’t have to think about these details. They just select HYBRIDSIG1 or HYBRIDSIG2 in their ciphersuite configuration, and cryptographers get to decide what that means.
TL;DR
Hybrid designs of post-quantum crypto are good, and I think composite hybrid designs make the most sense for both KEMs and signatures.https://soatok.blog/2022/01/27/the-controversy-surrounding-hybrid-cryptography/
#asymmetricCryptography #classicalCryptography #cryptography #digitalSignatureAlgorithm #hybridCryptography #hybridDesigns #KEM #keyEncapsulationMechanism #NISTPostQuantumCryptographyProject #NISTPQC #postQuantumCryptography

Earlier this week, NIST announced Round 3 of the Post-Quantum Cryptography project and published their rationale for selecting from the Round 2 candidates.
NIST did something clever this time, and Round 3 was separated into two groups: Finalists and Alternative Candidates.
Finalists are algorithms that NIST (and the majority of the cryptographers involved in NIST’s decisionmaking) believe are production-ready and worth standardizing immediately.
Meanwhile, Alternative Candidates are algorithms that NIST believes need a few more years of cryptanalysis and research before feeling confident about, for one reason or another.
I’m sure everyone in cryptography has their own opinions about the Round 3 selection, but I’d like to analyze the Round 3 finalists from a very opinionated, real-world perspective.
I’ll look at the alternative candidates in a future post.

Judgement Criteria
I will be evaluating Key Encapsulation algorithms based on real world operational requirements–rather than theoretical notions of security–for public key encryption and key encapsulation, namely:
- Feasibility to integrate with existing transport-layer protocols (TLS, Noise, etc.)
- Support for offline public-key encryption (a.k.a. “sealing”) APIs in application-layer cryptography.
This means you can encrypt with an online public key, but decryption requires a secret key that is kept offline and only accessed when needed.
I will be evaluating Digital Signature algorithms based on the following criteria:
- Statelessness: Can the algorithm be safely used in a virtual machine that gets rolled back?
- Bandwidth: Are signatures reasonably small?
Some people might object to this criteria, but this post is ultimately my opinion, and those are the criteria I care about the most.
Post-Quantum Key Encapsulation Round 3 Finalists
Classic McEliece
Classic McEliece is based on error-correcting codes.
Classic McEliece has large public keys (ranging from 261120 bytes to 1357824 bytes in the Round 2 submission) but short ciphertexts (128 to 240 bytes). This makes it difficult to implement Classic McEliece in protocols like TLS (since it will require a minimum of 4 TCP packets just to transmit a public key).
Classic McEliece does not have decryption failures, making it suitable for offline public-key encryption. However, the enormous public key may hinder adoption here too.
CRYSTALS-KYBER
CRYSTALS (Cryptographic Suite for Algebraic Lattices) encompasses two proposals: Kyber (key encapsulation) and Dilithium (signatures).
Kyber public keys range from 800 bytes (for Kyber-512) to 1568 bytes (for Kyber-1024) and ciphertexts range from 736 bytes to 1568 bytes, which means that Kyber can be easily used in protocols like TLS.
Kyber decryptions have a failure probability of about 1 in 2^160. While this probability is unlikely to ever occur in the real world, any nonzero failure probability baked into the algorithm does mean that encrypting a symmetric key with Kyber, strictly speaking, can prevent you from decrypting the symmetric key successfully. This makes it difficult to recommend Kyber in confidence for offline-decryption protocols, since there is no opportunity to recover from the (however improbable) error.
(This isn’t an argument that 2^-160 is too high. Any nonzero probability baked into any algorithm is still nonzero, and therefore irks me.)
NTRU
NTRU is another lattice-based scheme, and one of the oldest post-quantum lattice cryptosystems ever developed. (It’s so old that the patents have all expired.)
Like Kyber, NTRU offers small public keys (699 bytes for ntruhps2048509 on the low end, 1230 bytes for ntruhps4096821on the high end), making NTRU suitable for protocols like TLS that require small-ish public keys.
Like Kyber, NTRU boasts a decryption failure rate less often than 1 in 2^100 for all parameter sets. (The precise failure rates are not given in the NTRU specification document.) Strictly speaking, this might never be a practical concern, but it is still technically possible to encrypt something with NTRU that cannot be decrypted. This makes it difficult to recommend NTRU for this use case.
Update (2020-10-06): Paulo Barreto emailed me with a correction: NTRU’s submission for Round 2 boasts zero decryption failures.
SABER
SABER is another lattice-based key encapsulation algorithm. SABER’s security is based on a different problem than Kyber and NTRU. However, SABER gets bonus points for calling its lightweight mode LightSABER and using a lightsaber in their website’s design.
SABER offers small public keys (672 to 1312 bytes) and ciphertexts (736 to 1472 bytes). TLS should have no problem with SABER.
As with the other lattice-based proposals, the decryption failure probability is nonzero (2^-120 to 2^-165 for the SABER variants).
Round 3 Key Encapsulation Finalist Summary
If your only goal for post-quantum cryptography was to design primitives that can be used in online modes like TLS, then any of the lattice based proposals (Kyber, NTRU, SABER) are great.
For offline public-key encryption, all three of those proposals carry a nonzero risk of decryption failure, which can only really be mitigated by encrypting the same session key multiple times and storing multiple ciphertexts. (Update: See below.) This failure risk is already negligible (cosmic rays are more likely), but offline protocols have no recovery mechanism (whereas online protocols can just re-initiate a key exchange and call it a day).
One might argue that the probability is negligible (in fact, most cryptographers agree that a failure probability below 1 in 2^120 isn’t worth thinking about, since it will never happen in the real world), but I contend that a nonzero risk means they cannot be used in sealing APIs for general purpose cryptography libraries, since the developers of that library cannot be responsible for the decryption failure risk calculus for all of its users.
That is to say: In my humble opinion, in order to safely implement offline decryption, the algorithmic failure probability must be zero. Any nonzero algorithmic failure rate makes me grumpy (even if there’s no real-world, practical risk).
You might be tempted to just use Classic McEliece for sealing APIs, but since the public keys are enormous, I don’t see this being an option for constrained environments (i.e. embedded devices).
In short, I think the NIST PQC Round 3 finalists completely missed a use case that’s important to me, but apparently not important to NIST. (Offline decryption with a long-lived keypair.) Here’s hoping one or more of the non-lattice key encapsulation algorithms reaches maturity so we’re not caught in a catch-22.
Update (2020-10-06): I was mistaken about NTRU on two fronts:
- I had overlooked NTRU HRSS701 (as Bo-Yin Yang points out in the comments section).
- Round 2 of the NTRU NIST submission has a failure probability of zero (as Paulo Barreto informed me via email).
Given that NTRU is therefore suitable for offline public-key encryption (or, more to the point, offline HPKE), my above complaints about missed use-cases are therefore invalid. (However, for the sake of transparency, I’m only retracting them, not erasing them.)
Post-Quantum Digital Signature Round 3 Finalists
CRYSTALS-DILITHIUM

Dilithium is the signature counterpart to Kyber.
Dilithium is stateless. Public keys range between 1184 and 1760 bytes. Signatures range between 2044 bytes and 3366 bytes.
Nothing to complain about here.
FALCON
FALCON is difficult to implement, but it offers great performance and compact public keys (897 to 1793 bytes) and small signatures (~657 to ~1273 bytes). According to the Falcon website, Falcon-512 is about five times as fast as 2048-bit RSA.
Did I mention it’s stateless?
Rainbow

Rainbow is not a lattice-based scheme, in case you were sick of those. Instead it’s multivariate cryptography.
Rainbow public keys are somewhat large (149 KB to 1705.5 KB, although you can get 58.1 KB to 491.9 KB if you use compressed public keys). However, it boasts short signatures (64 bytes to 204 bytes).
Unlike the other schemes, the specification for Rainbow doesn’t spend a lot of time on introducing it in words. Instead, the paper just dives into the algorithm details without explaining “why?”.
Round 3 Digital Signature Finalist Summary
If you’re going to implement Kyber, it makes sense to also use Dilithium for signatures. Otherwise, FALCON’s performance is hard to beat.
Rainbow is interesting but requires large public keys and needs better documentation.
TL;DR
The Round 3 key encapsulation finalists are great for online encryption, but I don’t feel all warm and fuzzy about algorithms that possess an inherent decryption failure probability, which several of them do. McEliece’s enormous key and ciphertext sizes make it less attractive than the lattice-based candidates.
The Round 3 digital signature finalists are solid. I have a slight preference for FALCON but Dilithium looks great. I don’t know enough about Rainbow to evaluate it.
If I had to make any prediction about the PQC selection, it would be (in order of most-to-least likely to be selected, assuming anyone at NIST shares my priorities):
- Key encapsulation
- NTRU
- CRYSTALS-KYBER
- SABER
- Classical McEliece
- Digital signatures
- CRYSTALS-DILITHIUM
- FALCON
- Rainbow
(Excluding the alternative candidates, which merit a deeper analysis.)
Header art by Riley.
#asymmetricCryptography #ClassicalMcEliece #cryptography #Dilithium #FALCON #Kyber #lattices #NIST #NTRU #PQC #Rainbow #SABER
Earlier this week, NIST announced Round 3 of the Post-Quantum Cryptography project and published their rationale for selecting from the Round 2 candidates.NIST did something clever this time, and Round 3 was separated into two groups: Finalists and Alternative Candidates.
Finalists are algorithms that NIST (and the majority of the cryptographers involved in NIST’s decisionmaking) believe are production-ready and worth standardizing immediately.
Meanwhile, Alternative Candidates are algorithms that NIST believes need a few more years of cryptanalysis and research before feeling confident about, for one reason or another.
I’m sure everyone in cryptography has their own opinions about the Round 3 selection, but I’d like to analyze the Round 3 finalists from a very opinionated, real-world perspective.
I’ll look at the alternative candidates in a future post.
Art by Khia
Judgement Criteria
I will be evaluating Key Encapsulation algorithms based on real world operational requirements–rather than theoretical notions of security–for public key encryption and key encapsulation, namely:
- Feasibility to integrate with existing transport-layer protocols (TLS, Noise, etc.)
- Support for offline public-key encryption (a.k.a. “sealing”) APIs in application-layer cryptography.
This means you can encrypt with an online public key, but decryption requires a secret key that is kept offline and only accessed when needed.I will be evaluating Digital Signature algorithms based on the following criteria:
- Statelessness: Can the algorithm be safely used in a virtual machine that gets rolled back?
- Bandwidth: Are signatures reasonably small?
Some people might object to this criteria, but this post is ultimately my opinion, and those are the criteria I care about the most.
Post-Quantum Key Encapsulation Round 3 Finalists
Classic McEliece
Classic McEliece is based on error-correcting codes.Classic McEliece has large public keys (ranging from 261120 bytes to 1357824 bytes in the Round 2 submission) but short ciphertexts (128 to 240 bytes). This makes it difficult to implement Classic McEliece in protocols like TLS (since it will require a minimum of 4 TCP packets just to transmit a public key).
Classic McEliece does not have decryption failures, making it suitable for offline public-key encryption. However, the enormous public key may hinder adoption here too.
CRYSTALS-KYBER
CRYSTALS (Cryptographic Suite for Algebraic Lattices) encompasses two proposals: Kyber (key encapsulation) and Dilithium (signatures).Kyber public keys range from 800 bytes (for Kyber-512) to 1568 bytes (for Kyber-1024) and ciphertexts range from 736 bytes to 1568 bytes, which means that Kyber can be easily used in protocols like TLS.
Kyber decryptions have a failure probability of about 1 in 2^160. While this probability is unlikely to ever occur in the real world, any nonzero failure probability baked into the algorithm does mean that encrypting a symmetric key with Kyber, strictly speaking, can prevent you from decrypting the symmetric key successfully. This makes it difficult to recommend Kyber in confidence for offline-decryption protocols, since there is no opportunity to recover from the (however improbable) error.
(This isn’t an argument that 2^-160 is too high. Any nonzero probability baked into any algorithm is still nonzero, and therefore irks me.)
NTRU
NTRU is another lattice-based scheme, and one of the oldest post-quantum lattice cryptosystems ever developed. (It’s so old that the patents have all expired.)Like Kyber, NTRU offers small public keys (699 bytes for ntruhps2048509 on the low end, 1230 bytes for ntruhps4096821on the high end), making NTRU suitable for protocols like TLS that require small-ish public keys.
Like Kyber, NTRU boasts a decryption failure rate less often than 1 in 2^100 for all parameter sets. (The precise failure rates are not given in the NTRU specification document.)Strictly speaking, this might never be a practical concern, but it is still technically possible to encrypt something with NTRU that cannot be decrypted. This makes it difficult to recommend NTRU for this use case.Update (2020-10-06): Paulo Barreto emailed me with a correction: NTRU’s submission for Round 2 boasts zero decryption failures.
SABER
SABER is another lattice-based key encapsulation algorithm. SABER’s security is based on a different problem than Kyber and NTRU. However, SABER gets bonus points for calling its lightweight mode LightSABER and using a lightsaber in their website’s design.SABER offers small public keys (672 to 1312 bytes) and ciphertexts (736 to 1472 bytes). TLS should have no problem with SABER.
As with the other lattice-based proposals, the decryption failure probability is nonzero (2^-120 to 2^-165 for the SABER variants).
Round 3 Key Encapsulation Finalist Summary
If your only goal for post-quantum cryptography was to design primitives that can be used in online modes like TLS, then any of the lattice based proposals (Kyber, NTRU, SABER) are great.For offline public-key encryption,
all three of those proposals carry a nonzero risk of decryption failure, which can only really be mitigated by encrypting the same session key multiple times and storing multiple ciphertexts. (Update: See below.) This failure risk is already negligible (cosmic rays are more likely), but offline protocols have no recovery mechanism (whereas online protocols can just re-initiate a key exchange and call it a day).One might argue that the probability is negligible (in fact, most cryptographers agree that a failure probability below 1 in 2^120 isn’t worth thinking about, since it will never happen in the real world), but I contend that a nonzero risk means they cannot be used in sealing APIs for general purpose cryptography libraries, since the developers of that library cannot be responsible for the decryption failure risk calculus for all of its users.
That is to say: In my humble opinion, in order to safely implement offline decryption, the algorithmic failure probability must be zero. Any nonzero algorithmic failure rate makes me grumpy (even if there’s no real-world, practical risk).
You might be tempted to just use Classic McEliece for sealing APIs, but since the public keys are enormous, I don’t see this being an option for constrained environments (i.e. embedded devices).
In short, I think the NIST PQC Round 3 finalists completely missed a use case that’s important to me, but apparently not important to NIST. (Offline decryption with a long-lived keypair.) Here’s hoping one or more of the non-lattice key encapsulation algorithms reaches maturity so we’re not caught in a catch-22.
Update (2020-10-06): I was mistaken about NTRU on two fronts:
- I had overlooked NTRU HRSS701 (as Bo-Yin Yang points out in the comments section).
- Round 2 of the NTRU NIST submission has a failure probability of zero (as Paulo Barreto informed me via email).
Given that NTRU is therefore suitable for offline public-key encryption (or, more to the point, offline HPKE), my above complaints about missed use-cases are therefore invalid. (However, for the sake of transparency, I’m only retracting them, not erasing them.)
Post-Quantum Digital Signature Round 3 Finalists
CRYSTALS-DILITHIUM
Yes, that’s really the Dilithium logo.
Dilithium is the signature counterpart to Kyber.
Dilithium is stateless. Public keys range between 1184 and 1760 bytes. Signatures range between 2044 bytes and 3366 bytes.
Nothing to complain about here.
FALCON
FALCON is difficult to implement, but it offers great performance and compact public keys (897 to 1793 bytes) and small signatures (~657 to ~1273 bytes). According to the Falcon website, Falcon-512 is about five times as fast as 2048-bit RSA.Did I mention it’s stateless?
Rainbow
No, not that kind of Rainbow! Probably. (Art by LindseyVi)
Rainbow is not a lattice-based scheme, in case you were sick of those. Instead it’s multivariate cryptography.
Rainbow public keys are somewhat large (149 KB to 1705.5 KB, although you can get 58.1 KB to 491.9 KB if you use compressed public keys). However, it boasts short signatures (64 bytes to 204 bytes).
Unlike the other schemes, the specification for Rainbow doesn’t spend a lot of time on introducing it in words. Instead, the paper just dives into the algorithm details without explaining “why?”.
Round 3 Digital Signature Finalist Summary
If you’re going to implement Kyber, it makes sense to also use Dilithium for signatures. Otherwise, FALCON’s performance is hard to beat.Rainbow is interesting but requires large public keys and needs better documentation.
TL;DR
The Round 3 key encapsulation finalists are great for online encryption, but I don’t feel all warm and fuzzy about algorithms that possess an inherent decryption failure probability, which several of them do. McEliece’s enormous key and ciphertext sizes make it less attractive than the lattice-based candidates.The Round 3 digital signature finalists are solid. I have a slight preference for FALCON but Dilithium looks great. I don’t know enough about Rainbow to evaluate it.
If I had to make any prediction about the PQC selection, it would be (in order of most-to-least likely to be selected, assuming anyone at NIST shares my priorities):
- Key encapsulation
- NTRU
- CRYSTALS-KYBER
- SABER
- Classical McEliece
- Digital signatures
- CRYSTALS-DILITHIUM
- FALCON
- Rainbow
(Excluding the alternative candidates, which merit a deeper analysis.)
Header art by Riley.
#asymmetricCryptography #ClassicalMcEliece #cryptography #Dilithium #FALCON #Kyber #lattices #NIST #NTRU #PQC #Rainbow #SABER

Last year I wrote a grab-bag post titled, Don’t Forget To Brush Your Fur, because I’m terrible at SEO or making content easily discoverable.
In the same vein as that previous example, this is going to be in the style of Lightning Round talks at technology conferences.
Why are we doing this again?
I maintain a running list of things to write about, and cross ideas off whenever I cover a topic.
After a few months of doing this, I realize most of what remains is kinda interesting but not quite interesting enough to warrant a dedicated entry.

(Art by Lynx vs Jackalope)
Contents
- Asymmetric Key Wear-Out
- HMAC Wear-Out?
- Asymmetric Commitments
- Against “Fluffies”
- A Meditation on Furries and Cringe
- Furries and Blue State Privilege
Asymmetric Key Wear-Out
Last year, I wrote about cryptographic wear-out for symmetric encryption. That post has attracted quite a bit of feedback from folks requesting comparisons against other block cipher modes, etc. One topic that I didn’t see requested much, but is equally interesting, is how this reasoning can be applied to asymmetric cryptography (if at all).
Let’s get one thing clear: Cryptography keys don’t “wear out” in the same sense as a physical key might. What we’re talking about is an ever-increasing risk of a collision occurring in random nonces.
ECDSA Key Wear-Out
ECDSA signatures involve a one-time secret, k. The scalar multiplication of k and the base point for the curve is encoded as half of the signature (r), while its modular inverse is multiplied by the sum of the truncated message hash and the product of r and the secret key to produce the other half of the signature (s).
If your selection of k is biased, or k is ever reused for two different messages, you can leak the secret key.
Strictly speaking, for any given ECDSA curve, there is only one k value that corresponds to a given r for all users (n.b it’s not distinct per keypair).
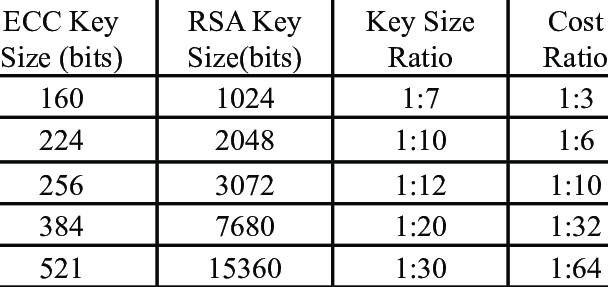
This means that all users of e.g. ECDSA over NIST P-256 have to worry about a shared cryptographic wear-out: After 2^112 signatures, there is a 2^-32 chance of a single collision occurring.
Fortunately, the search space of possible k-values is enormous, and this will not impose a real-world operational risk in the near future. If you’re worried about multi-user attacks, P-384 gives you a wear-out threshold of 2^176 messages, which we’re probably never going to achieve.
RSA Key Wear-Out
In order to calculate the wear-out for an RSA message, you first have to begin with an attack model. Previously, we were looking at algorithms that would become brittle if a nonce was reused.
RSA doesn’t have nonces. You can’t attack RSA this way.
But let’s assume that such an attack did exist. What might the safety limit look like? There are two remaining possible considerations for RSA’s security against cryptographic wear-out: Key size and padding mode.
RSA private keys are two prime numbers (p, q). RSA public keys are the product of the two primes (n) and a public exponent (e) that must be coprime to (p-1)(q-1). (In practice, e is usually set to 3, 65537, or some other small prime.)
The security of RSA is subexponential to key size, based on the difficulty of integer factoring attacks and the requirement for p and q to be prime numbers.
This primeness restriction doesn’t apply to your message. The padding mode dictates your upper limit on message size; e.g., PKCS#1 v1.5 padding will take up at least 3 bytes:
- For encryption,
x = 0x00 || 0x02 || r || 0x00 || m, whereris random padding bytes (minimum 8 bytes). - For signatures,
x = 0x00 || 0x01 || 0xFF..FF || 0x00 || m. - In either case, the padding is always at least 11 bytes long.
So if you have 2048-bit RSA keys, you can encrypt or sign up to 245 bytes (1960 bits) with PKCS#1 v1.5 padding. This corresponds to a safety limit of 2^974 messages.

HMAC Wear-Out?
To keep things simple, the security of HMAC can be reduced to the collision risk of the underlying hash function.
If you’re trying to estimate when to rotate symmetric keys used for HMAC, take the birthday bound of the underlying hash function as your starting point.
- For SHA-256, you have a 50% chance of a collision after 2^128 messages. For a 2^-32 chance, you can get 2^112 messages out of a single key.
- For SHA-384, this is 2^176 messages.
- For SHA-512, this is 2^240 messages.
In either case, however, these numbers might as well be infinity.

Asymmetric Commitments
Did you know that fast MACs such as GHASH and Poly1305 aren’t random-key robust? This property can matter in surprising ways.
Did you know that ECDSA and RSA don’t qualify for this property either? This is related to the topics of malleability and exclusive ownership. You can learn more about this in the CryptoGotchas page.
Essentially, if a signature scheme is malleable or fails to provide exclusive ownership, it’s possible to construct two arbitrary (m, pk) pairs that produce the same signature.
Any nonmalleable signature scheme with exclusive ownership (i.e. Ed25519 with low-order point rejection and canonical signature checks, as provided by the latest version of libsodium) provides sufficient commitment–mostly due to how it uses a collision-resistant cryptographic hash function. (It’s also worth noting: HashEdDSA doesn’t. Isn’t cryptography fun?)
Generally, if you need random-key robustness, you want to explicitly make it part of your design.
Against “Fluffies”
In my blog post about the neverending wheel of Furry Twitter discourse, I mentioned the controversy around SFW spaces for underage furries.
Everything I said in that post is still accurate (go read it if you haven’t), but I want to emphasize something that maybe some people overlooked.
https://twitter.com/SoatokDhole/status/1426638694786682884
Underage furries calling themselves “fluffies” is a bad idea, for two reasons.
Divide and Conquer
The first reason is tactical, and not specific to what they’re calling themselves: If you label yourselves separately from the larger furry community, you make it much easier to be targeted–especially by propaganda. There’s a severely disturbed alt-right fringe to the furry fandom (dubbed alt-furry, the Furry Raiders, and so many other names) that would love nothing more than to sink their claws into younger furs.
It’ll start innocently enough (“Yay, you have your own space!”), but it will quickly accelerate (“Congrats on kicking those degenerates to the curb!”) to horrible places (“All LGBTQIA+ people are degenerates”), gliding on the wings of edgy humor.
This descent into madness is also known as the PewDiePipeline and all parents of furries should be made aware of it, lest it happen to their child:
https://www.youtube.com/watch?v=pnmRYRRDbuw
It bears emphasizing: This existence of a PewDiePipeline within the “fluffy” space is not predicated on the intentions of the proponents. They can have all the best intentions in the world and it will still happen to their microcosm.
https://twitter.com/ARCADEGUTS/status/1425687280983937027
Preventing this from happening will require an almost inhuman degree of vigilance and dedication to correcting discourse from going sour. None of us are omniscient, so I wouldn’t take that bet.
Pre-Existing Terminology
The second reason the “fluffies” label is a bad idea is more specific to the word “fluffies” in particular: It already refers to a very disturbing meme on 4chan from not-very-many years ago: Fluffy Abuse Threads.
I’m intentionally not including any videos or images of this topic. There just aren’t enough content warnings for how gross this content is.
By calling yourselves “fluffies”, the most deranged 4chan-dwellers and/or Kiwi Farms lurkers on the Internet will begin associate you with the “fluffy abuse” memes, and may even act accordingly. In their twisted minds, they may even rationalize their conduct as if somehow you’re consenting to the abuse, by virtue of what you call yourselves.
Look, I get it: When you’re young, the over-sexualization of the media can be very uncomfortable, and it’s natural to want to avoid it. Additionally, it’s only human to want your own special club with a special name to hang out with your exclusive (n.b. same-age) community.
But please think carefully about what you’re doing, how you’re doing it, and which adults you decide to trust.
Also: maybe talk to older queers and/or furries about the history of the Furry Fandom, Pride, and kink before you make dangerous moves that make you more vulnerable to the worst humanity has to offer? Even if you don’t agree with us, we don’t want to see you get hurt.
There definitely is room in the furry fandom for people who are not comfortable with sexual content, or simply don’t want to be inundated with it all the damn time. It doesn’t need to be an exclusive thing or concept; instead, it should be normalized.
Ultimately, there’s probably a lot of work to be done to ensure kids and families have a safe and enjoyable furry con experience during daylight hours without repressing the queer and sexual identities of consenting adults at night. The best way to get from here to there is to talk, not to isolate.
Otherwise, we’ll keep seeing occurrences like this:
https://twitter.com/PrincelyKaden/status/1426192114694692866
The onus here is going to be largely on furry convention staff and chatroom moderators to actually listen to people reporting abusive behavior. They haven’t always been good about that, and it’s time for change.
https://twitter.com/MegaplexCon/status/1425966589241970693
A Meditation on Furries and Cringe
Every once in a while, I get a comment or email like this one:
https://twitter.com/SoatokDhole/status/1360835077899436033
The biggest magnet for poorly-reasoned hate comments is, surprisingly, my tear-down of the “sigma male” meme.
You’d think the exposure of TheDonald’s non-CloudFlare IP address would draw more ire than having correct opinions on masculinity, but here we are.

Let’s talk about masculinity for a moment, guys.
There is nothing manlier than being your authentic self. Even if that means liking some “girly” things. Even if that means being soft and vulnerable at times. Even if that means actually conforming to some stereotypes perpetuated by toxic masculinity when it coincides with your likes and interests. You do you.
But this isn’t just true of the male gender. Authenticity is the epitome of humanity. There’s nothing that stops women and enbies from being ruthlessly themselves.
You can’t be authentic when you’re participating in Cringe Culture, which blindly tears large swaths of people down to stoke the feelings of superiority in the people who evade its blast.
People are weird. I’m weird. I don’t expect everyone to like me, nor do I want them to. (Parasocial relationships suck!)
It’s okay to be a little obsessed about something other people look down on just because you happen to like it. Just make sure you’re not eschewing your adult responsibilities. (We all have bills to pay and promises to keep to the people that matter to us.)
If people don’t like you because you suddenly revealed your fondness for classic video games, rock-tumbling, or linear algebra? Fuck ’em. May the bridges you burn light the way to people who will appreciate you for who you truly are.
I’ve been told my blog is “weapons grade cringe” before, because I dared talk about encryption while having what, to most adults, comes across as little more than a cartoon brand or company mascot.

Furries and Blue State Privilege
I sympathize with most queer people and/or furries for not wanting to subject themselves to the bigotry that runs rampant in Red States, but the ones who are jerks to other members of their community for living in those states, I can do without.
https://twitter.com/SarahcatFursuit/status/1413566747148435456
Being an asshole to someone because they live in, or are moving to, a state whose politics you dislike is equal parts stupid, selfish, and self-defeating:
- It’s stupid because there’s no reason for expressing prejudice or painting with broad brushes. For example: “Florida Furs are bad people” is an attack on the author of this blog.
- It’s selfish because not everyone who wants to leave these states has the resources or opportunity to do so, so all you’re doing is shining a spotlight on your own privilege. Way to show your entire ass to the community.
- It’s self-defeating because of the way the U.S. political system is architected:
If you wished for a genie to move every LGBTQIA+ person to the west coast of the United States, within a few years you’d essentially reduce support for LGBTQIA+ rights to approximately 6 out of 100 votes in the US Senate and 68 out of 435 in the House of Representatives.When you factor in who owns the land in the big tech cities (San Francisco, Seattle, etc.) and how much political and economic power they wield, it becomes very clear that your shaming of others for not boarding the bandwagon serves the interests of the worst of humanity: Landlords and venture capitalists.
Not a good move for people who claim to be progressive, and want to achieve progressive political outcomes nationwide.
The fact that some states have horrendous laws on the books, even worse bastards enforcing these laws, and somehow even more terrible politicians gatekeeping any meaningful progress from changing the system isn’t ever going to be improved from the outside.
I say all this, and I acknowledge Florida does suck in a lot of obvious ways: Our governor (Ron DeSantis) has a disposition that would actually be improved if he wore clown make-up to press appearances. We also have far too many furries that are anti-maskers, anti-vaxxers, or both.
https://twitter.com/SoatokDhole/status/1300911840000708608
But when furries go out of their way to shame someone, simply for living here? You’re not helping. Seriously stop and think about your priorities.
And maybe–just maybe–be surgically precise when you decide insults are warranted.
Now that I’ve flushed the blog post topic buffer, I’m fresh out of ideas. Let me know some topics that interest you in my Telegram group so I don’t get bored and eventually write Buzzfeed-quality crap like this:

https://soatok.blog/2021/08/16/lightning-round/
#asymmetricCryptography #ECDSA #Florida #furries #FurryFandom #HMAC #Politics #RSA #Society #wearOut
There are a lot of random topics I’ve wanted to write about since I started Dhole Moments, and for one reason or another, haven’t actually written about. I know from past experience with other projects that if you don’t occasionally do some housekeeping, your backlog eventually collapses under its own gravity and you can never escape from it.So, to prevent that, I’d like to periodically take some time to clean up some of those loose ends that collect over time.
Random-Access AEAD
AEAD stands for Authenticated Encryption with Associated Data. Typically, AEAD constructions involve a stream cipher (which may also be a block cipher in counter mode) and a message authentication code (which may also be an almost-universal hash function).AEAD modes are designed for one-shot APIs: Encrypt (then authenticate) all at once; (verify then) decrypt all at once. AES-GCM, ChaPoly, etc.
AEADs are less great at providing random access to the underlying plaintext. For example: If you’re encrypting a 240 GB file with AES-GCM, but you only need a 512 KB chunk at some arbitrary point in the file, you’re forced to choose between either:
- Authenticating the rest of the AES-GCM ciphertext, then decrypting only the relevant chunk. (Performance sucks.)
- Sacrificing integrity and decrypting the desired chunk with AES-CTR.
Being forced to choose between speed and security will almost certainly result in a loss of security. The incentives of software developers (especially with fly-by-night startup engineers) all-but-guarantee this outcome.
Consequently, there have been several implementations of streaming-friendly AEAD. The most famous of which is Phil Rogaway’s STREAM construction.
Source: Rogaway’s paper
The downside to STREAM is that it requires an additional T bytes (e.g. 16 for an 128-bit authentication tag) for each chunk of the plaintext.
A similar solution, as implemented in the AWS Encryption SDK, is to carefully separate plaintexts into equal-sized frames and have special rules governing IV/nonce selection. This lets you facilitate random access while still making the security of the whole system easy to reason about.
Can we do better than STREAM and message framing?
The most straightforward idea is to use a Merkle tree on the ciphertext with a stream cipher for extracting a distinct key for each leaf node. This can be applied to existing AEAD ciphertexts, out of band, to create a sort of deep authentication tag that can be used to authenticate any random subset of the message (provided you have the correct nonce/key).
However, I haven’t found the time to develop this idea into something that can be toyed with by myself and other researchers.
More Introductory Articles
Let’s face it:
Art by Riley
I’ve previously suggested an alternative strategy for programmers to learn cryptography. I’d like to do more posts covering introductory material for the topics I’m familiar with, so anyone who wants to actually employ my proposed strategy can carry themselves across the finish line.
Dissecting Dog-Whistles
Random fact: My fursona is a dhole–also known as a whistling dog.
Soatok is a dhole, not a fox. Art by Khia.
Coincidentally, I’m deeply fascinated by language, and planned to start a series analyzing dog-whistle language (especially the kind commonly used against queer subcultures).
However, the very nature of dog-whistle language provides a veneer of plausible deniability for the whistler’s intent, which makes it very difficult to address them in a meaningful way that doesn’t undermine your own credibility.
So, for the time being, this is on the back-burner.
Reader Questions
I’ve received quite a few questions via email and social media since I started this blog in April. The most obvious thing to do with these questions would be to periodically collate a bunch of them into a Questions and Answer style post.However! I have an open source projected called FAQ Off that is way more efficient at the Q&A format than a long-form blog post. If you’d like to see it in action, start here.
Art by Kyume
General Punditry
I make a lot of dumb jokes, typically involving puns and other wordplay. Most of these live in private Telegram conversations with other furries, but a few have leaked out onto Twitter over the years.Is automated vulnerability scanning a nessusity?— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) November 23, 2017
Nurse: "I suspect this patient attempted to shove a foreign object into their urethra for pleasure"
Doctor: "I believe your theory is sound"
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) June 25, 2018
A lot of them involve queer lingo.
People say it's lonely at the top.No wonder there's so many bottoms in this fandom 😛
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) December 30, 2019
BitTorrent users are thirsty bottoms. Always complaining about wanting more seed.
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) August 4, 2019
My RAID controller has big disk synergy
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) August 1, 2018
Some of them involve furry in-jokes.
Q) Why are foxes so prevalent in the furry fandom?A) We're a sub-culture not a dom-culture.
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) May 24, 2018
Intrusion detection systems are old hat. What we need is a protrusion detection system.
Introducing OwO
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) February 1, 2018
Some are just silly.
Using mined bitcoins to buy a pumpkin spice latte makes you an ASIC bitch, right?— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) February 6, 2018
So in gay male furry culture if you give into a booty call from your ex-boyfriend… does that mean you were craving the XD?
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) August 25, 2018
If SQL is pronounced "sequel" then PHP must be pronounced "fap".
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) July 23, 2019
What do you call a submissive dragon with a mathematics background who's already lubed up for you?
A sliding scale.
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) December 26, 2018
Did you hear about the clairvoyant babyfur that broke RSA?
Turns out, all you needed was a padding oracle.
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) October 1, 2017
I should look for my next partner in a nuclear chemistry lab.
I hear they're good at dating.
— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) December 8, 2016
In my humble opinion, there haven’t been nearly enough puns on this blog (unless the embedded tweets above count).
Normally, this is where I’d proclaim, “I shall rectify this mistake” and proceed to make an ass out of myself, but I don’t like forced and obvious puns.
A lot of furries get this wrong: “Pawesome” is not clever, unless you’re talking to someone with a marsupial fursona. Then maybe.
The best puns come in two forms: They’re either so clever that you never saw it coming, or they’re just clever enough that the punchline lands at the same time you realized a bad pun was even possible.
Only Soatok brand puns are 100% whole groan— Mastodon: soatok@furry.engineer, Cohost: soatok (@SoatokDhole) January 26, 2018
Miscellaneous / Meta
The past few blog posts touched a little on political subjects (especially How and Why America Was Hit So Hard By COVID-19, but this short-term trend actually started with my Pride Month post).At some point in the future, I may write a post dedicated to politics, but for the time being, it’s not really a subject I care enough about in and of itself to emphasize all the time.
Let me be clear: Being gay in America is inherently political. Developing technology is inherently political (although you don’t always realize it). Being a gay technologist, saying something politically significant is an inevitability.
But I’m not interested in the traditional roles and narratives that infect politics and political discourse. Labels are stupid and I’m not interested in being a Useful Idiot for anyone’s propaganda.
The most difficult thing about writing blog posts for me is coming up with a meaningful title. I’ve lost many hours due to the writer’s block that ensues.
The second most difficult thing for me is writing closing statements that aren’t totally redundant.
https://www.youtube.com/embed/l44OV2jlN7A?start=665&feature=oembed
George Carlin – “Count the Superfluous Redundant Pleonastic Tautologies” – Skip to 11:05 if WordPress breaks something
Some bloggers like to sign off like they’re writing an email. “Happy hacking!” and whatnot. To me, this feels forced and inauthentic, like a bad pun.So instead, here’s a totally sick piece of art I got from @MrJimmyDaFloof.
Furry artists are, like the rest of the fandom, amazing.
https://soatok.blog/2020/07/07/dont-forget-to-brush-your-fur/

Neil Madden recently wrote a blog post titled, Digital Signatures and How to Avoid Them. One of the major points he raised is:
Another way that signatures cause issues is that they are too powerful for the job they are used for. You just wanted to authenticate that an email came from a legitimate server, but now you are providing irrefutable proof of the provenance of leaked private communications. Oops!Signatures are very much the hammer of cryptographic primitives. As well as authenticating a message, they also provide third-party verifiability and (part of) non-repudiation.
Neil Madden
Later, he goes on to make recommendations for alternatives. Namely HMAC, possibly with a KEM. His recommendations are sensible and straightforward.
Where’s the fun in that, though?
Let’s design a type of digital signature algorithm that can only be verified by the intended recipients.
Standard Crypto Disclaimer
Don’t use any of this.
I’m rolling my own crypto, which is almost always a bad idea, for my own amusement.
Absolutely none of this has been peer-reviewed or audited.
Even if there’s no immediately obvious fatal flaw in this design, it’s always possible that I screwed something up.
If anything of value ever comes of this post, it will be serious cryptographers writing their own protocol that accomplishes the goals set out in this furry blog post, but with a machine verifiable security proof.
X3MAC
Let’s start with a somewhat simple building block (using libsodium), which I call X3MAC.
Why? Because it’s partly inspired by X3DH.
The idea is pretty straightforward, and basically in line with what Neil recommended:
- Generate an ephemeral keypair.
- Do two ECDHs. One between the sender and the recipient, the other between the ephemeral keypair and the recipient.
- Use a domain-separated hash with both ECDH outputs and all three public keys to obtain a symmetric key.
- Calculate a MAC over the message, using the symmetric key.
- Return the ephemeral public key and MAC.
Verification is basically deriving the same symmetric key from the recipient’s perspective, recalculating the MAC, and comparing the two in constant-time.
This should be pretty easy to understand.
Why bother with ephemeral keypairs?
It doesn’t buy us much for the MAC use-case (since we aren’t encrypting so forward secrecy isn’t a consideration), but we will use it when we turn the X3MAC into X3SIG.
What are people saying about X3MAC?
When I showed X3MAC to some friends, some recoiled in horror and others said, “Oh, I think I have a use case!”
I really hope they’re joking. But out of caution, this is where I will cease to provide sample code.
Sarah Jamie Lewis said, “thank you i hate this.” That’s probably the correct response.
Turning X3MAC into a Signature
X3MAC isn’t actually very useful.
If Alice and Bob use X3MAC, it’s true that only the two of them can verify the authentication tag for a message… but both parties can also create authentication tags.
To turn this into a signature algorithm, we need to work with the Ristretto group and build a non-interactive variant of Schnorr’s identification protocol.
My modified protocol, X3SIG, uses Ristretto255 scalars and points instead of X25519 keypairs.
“What does any of that even mean?“Ristretto255 is a prime-order group (imagine a clock, but instead of numbers going from 1 to 12, it’s between 0 and a very large prime number), built from Curve25519.
Scalars are analogous to secret keys.
Points are analogous to public keys.
You can do point arithmetic. You can do scalar arithmetic. You don’t have to worry about the cofactor (like you would with Ed25519 or X25519).
Schnorr’s identification protocol (explained above) is essentially the basis of elliptic curve signatures; i.e., you can construct EdDSA out of it with minor (yet important) tweaks.
That’s exactly what we’re doing here: Turning X3MAC into a signature by building Schnorr out of it.
The protocol begins the same way as X3MAC: Generate a random scalar, multiply it by the base point to get a point. Do some point-scalar multiplications and a domain-separated hash to derive a symmetric key. Hash the message with the symmetric key.
But this time, we don’t stop there. We use the X3MAC-alike hash in place of the Hash() step in non-interactive Schnorr.
Important: We can eschew some data from the hashing step because certain parameters are fixed by virtue of using Ristretto255.If anyone ever builds something on another group, especially one where these parameters can change, you MUST also include all of them in the hash.
If you fail to do this, you will find yourself vulnerable to weak Fiat-Shamir attacks (e.g., Frozen Heart). If you’re writing Rust, check out Decree for transcript hashing.
(As stated before: No sample code will be provided, due to not wanting people to ship it to production.)
What does this give us?
Alice can sign a message that only she and Bob can verify. Bob cannot generate a new signature. Third parties cannot perform either action.
Thus, we still have a digital signature, but not one that provides third-party verifiability.
X3INU – Cryptographic Innuendos
If we had stopped the train at X3SIG, that’d be pretty neat.
However, X3SIG is limited to one sender and one recipient. This is kind of a bummer that doesn’t scale very well.
Fortunately, this is a solvable problem.
If you recall from my idea for multicast support in Noise-based protocols, I’m no stranger to reusing the TreeKEM abstraction from the MLS RFC to nerd-snipe my friends in the cryptography community.
So let’s do that here.
X3INU.Pack
Inputs:
- 1 keypair (sk, pk)
- A finite number of other public keys (
pk_ifor many values ofi)
Output:
- Group public key
gpk
Here, we use a Ratchet Tree (per RFC 9420) where each step is a scalar multiplication over the Ristretto group (since that’s what everyone’s public key is) and a Key Derivation Function.
The important property is that each participant in the Pack can asynchronously derive the group secret key, and it’s computationally infeasible to do so without one of the pack members’ secret keys.
This step must be performed ahead of time to establish the Pack (quorum of recipients that can verify a signature).
X3INU.Howl
Inputs:
- The message being signed.
- The secret key for the entity sending the message.
- The pack public key for all of the recipients.
Outputs:
- A signature that only pack members can validate.
Here, we just perform an X3SIG signature with the pack public key.
X3INU.Hear
Inputs:
- The message being signed.
- The signature.
- The public key for the entity sending the message.
- The secret key for a pack member.
- The pack public key for all other recipients.
Outputs:
- Boolean (is the signature valid?)
Here, we just perform an X3SIG validation.
If you’re a member of the pack that can validate the signature, you can derive the group secret key and perform X3SIG as usual.
If you’re not, you can’t tell if the signature is valid or not. To you, it should be indistinguishable from random.
X3INU Questions and Answers
Why “X3INU”?
It’s short for “innuendo”, but also “inu” is the Japanese word for “dog”, and I like to make furry puns.
Why “Pack”, “Howl”, and “Hear”?
See above! Furry puns!
Why are you like this?
I dunno.
You fool, this already exists in the cryptographic literature under a different name! What do you have to say for yourself?
Okay, yeah, probably.
I’m not an academic, so if I reinvented something that someone else made (except worse, because this is being published on a furry blog for fun), that’s kind of cool but not surprising.
It also shouldn’t be surprising that I haven’t heard of it before, due to me not being an academic.
(The closest I’ve heard of are designated verifier signatures, as Neil Madden alluded to at the bottom of his blog post.)
What if I think this might actually be useful?
Normally, I would say, “Talk to a cryptographer before writing any code,” especially if you’re writing your own protocol that uses a Fiat-Shamir transform like I did here.
However, if it turns out that X3INU is in any way novel or valuable, you should instead consult the entire cryptographic community and wait for their verdict on whether this idea is totally bonkers or not.
Why not just public-key-encrypt a digital signature?
Why not just use the existing digital signature algorithms, but encrypt it under the recipients’ public keys?
Because after decryption, the recipient possesses a signature that a third-party could still use to verify the contents of a communication.
If you transmit the signatures produced by X3INU, only the audience can tell if they’re genuine or not.
(This assumes your audience’s secret keys all remain secret, of course.)
Under what conditions do the security guarantees fall apart?
If the signer reveals their secret key, messages can be forged.
If one of the Pack members reveals their secret key, anyone can verify signatures again.
If one of the Pack members leaks the internal hash used for a given message, anyone who knows this hash can verify the signature. Pack members can do this without compromising their own signing key.
This leakage is possible because the signature is computed over a keyed hash, and the key used by the hash is a shared secret between the signer and the recipients.
Thanks to Thad for inquiring about this:
could Bob not reveal the shared symmetric key from the X3MAC to a third party? His private key is still protected by mixing the ephemeral key and the KDF, while having the shared key allows the third party to verify the message hash and prove it with Alice’s public signing key(?)
Additionally, nothing about this protocol is post-quantum secure.
Couldn’t you extend X3MAC instead of X3SIG for the Innuendo protocol?
Yes. It may even be desirable to do so. After all, designated-verifier proofs already exist, and the recipients must be able to forge signatures.
The only downside is: Anyone in the quorum can forge messages, so there is no special “signer” role, really.
With that in mind, you’re probably better off just using a Ratchet Tree to get a shared secret, and then using that with HMAC.
Can we make it even more wild?
Here’s a fun one: Combine the idea behind innuendos (as outlined above) with ring signatures.
Now Alice is one indeterminate member of a discrete set of potential signers, rather than just one, who can sign a message such that only a designated group of recipients can verify (provided nobody’s secret key is leaked).
Header art by Harubaki and CMYKat.
https://soatok.blog/2024/09/20/cryptographic-innuendos/
#asymmetricCryptography #cryptographicInnuendos #RatchetTrees
Wikipedia’s definition of a digital signature is:A digital signature is a mathematical scheme for verifying the authenticity of digital messages or documents. A valid digital signature on a message gives a recipient confidence that the message came from a sender known to the recipient.—Wikipedia
They also have a handy diagram of the process by which digital signatures are created and verified:Source: https://commons.m.wikimedia.org/wiki/File😛rivate_key_signing.svg#mw-jump-to-license (CC-BY-SA)
Alice signs a message using her private key and Bob can then verify that the message came from Alice, and hasn’t been tampered with, using her public key. This all seems straightforward and uncomplicated and is probably most developers’ view of what signatures are for and how they should be used. This has led to the widespread use of signatures for all kinds of things: validating software updates, authenticating SSL connections, and so on.But cryptographers have a different way of looking at digital signatures that has some surprising aspects. This more advanced way of thinking about digital signatures can tell us a lot about what are appropriate, and inappropriate, use-cases.
Identification protocols
There are several ways to build secure signature schemes. Although you might immediately think of RSA, the scheme perhaps most beloved by cryptographers is Schnorr signatures. These form the basis of modern EdDSA signatures, and also (in heavily altered form) DSA/ECDSA.The story of Schnorr signatures starts not with a signature scheme, but instead with an interactive identification protocol. An identification protocol is a way to prove who you are (the “prover”) to some verification service (the “verifier”). Think logging into a website. But note that the protocol is only concerned with proving who you are, not in establishing a secure session or anything like that.
There are a whole load of different ways to do this, like sending a username and password or something like WebAuthn/passkeys (an ironic mention that we’ll come back to later). One particularly elegant protocol is known as Schnorr’s protocol. It’s elegant because it is simple and only relies on basic security conjectures that are widely accepted, and it also has some nice properties that we’ll mention shortly.
The basic structure of the protocol involves three phases: Commit-Challenge-Response. If you are familiar with challenge-response authentication protocols this just adds an additional commitment message at the start.
Alice (for it is she!) wants to prove to Bob who she is. Alice already has a long-term private key, a, and Bob already has the corresponding public key, A. These keys are in a Diffie-Hellman-like finite field or elliptic curve group, so we can say A = g^a mod p where g is a generator and p is the prime modulus of the group. The protocol then works like this:
- Alice generates a random ephemeral key, r, and the corresponding public key R = g^r mod p. She sends R to Bob as the commitment.
- Bob stores R and generates a random challenge, c and sends that to Alice.
- Alice computes s = ac + r and sends that back to Bob as the response.
- Finally, Bob checks if g^s = A^c * R (mod p). If it is then Alice has successfully authenticated, otherwise it’s an imposter. The reason this works is that g^s = g^(ac + r) and A^c * R = (g^a)^c * g^r = g^(ac + r) too. Why it’s secure is another topic for another day.
Don’t worry if you don’t understand all this. I’ll probably do a blog post about Schnorr identification at some point, but there are plenty of explainers online if you want to understand it. For now, just accept that this is indeed a secure identification scheme. It has some nice properties too.
One is that it is a (honest-verifier) zero knowledge proof of knowledge (of the private key). That means that an observer watching Alice authenticate, and the verifier themselves, learn nothing at all about Alice’s private key from watching those runs, but the verifier is nonetheless convinced that Alice knows it.
This is because it is easy to create valid runs of the protocol for any private key by simply working backwards rather than forwards, starting with a response and calculating the challenge and commitment that fit that response. Anyone can do this without needing to know anything about the private key. That is, for any given challenge you can find a commitment for which it is easy to compute the correct response. (What they cannot do is correctly answer a random challenge after they’ve already sent a commitment). So they learn no information from observing a genuine interaction.
Fiat-Shamir
So what does this identification protocol have to do with digital signatures? The answer is that there is a process known as the Fiat-Shamir heuristic by which you can automatically transform certain interactive identification protocols into a non-interactive signature scheme. You can’t do this for every protocol, only ones that have a certain structure, but Schnorr identification meets the criteria. The resulting signature scheme is known, amazingly, as the Schnorr signature scheme.You may be relieved to hear that the Fiat-Shamir transformation is incredibly simple. We basically just replace the challenge part of the protocol with a cryptographic hash function, computed over the message we want to sign and the commitment public key: c = H(R, m).
That’s it. The signature is then just the pair (R, s).
Note that Bob is now not needed in the process at all and Alice can compute this all herself. To validate the signature, Bob (or anyone else) recomputes c by hashing the message and R and then performs the verification step just as in the identification protocol.
Schnorr signatures built this way are secure (so long as you add some critical security checks!) and efficient. The EdDSA signature scheme is essentially just a modern incarnation of Schnorr with a few tweaks.
What does this tell us about appropriate uses of signatures
The way I’ve just presented Schnorr signatures and Fiat-Shamir is the way they are usually presented in cryptography textbooks. We start with an identification protocol, performed a simple transformation and ended with a secure signature scheme. Happy days! These textbooks then usually move on to all the ways you can use signatures and never mention identification protocols again. But the transformation isn’t an entirely positive process: a lot was lost in translation!There are many useful aspects of interactive identification protocols that are lost by signature schemes:
- A protocol run is only meaningful for the two parties involved in the interaction (Alice and Bob). By contrast a signature is equally valid for everyone.
- A protocol run is specific to a given point in time. Alice’s response is to a specific challenge issued by Bob just prior. A signature can be verified at any time.
These points may sound like bonuses for signature schemes, but they are actually drawbacks in many cases. Signatures are often used for authentication, where we actually want things to be tied to a specific interaction. This lack of context in signatures is why standards like JWT have to add lots of explicit statements such as audience and issuer checks to ensure the JWT came from the expected source and arrived at the intended destination, and expiry information or unique identifiers (that have to be remembered) to prevent replay attacks. A significant proportion of JWT vulnerabilities in the wild are caused by developers forgetting to perform these checks.
WebAuthn is another example of this phenomenon. On paper it is a textbook case of an identification protocol. But because it is built on top of digital signatures it requires adding a whole load of “contextual bindings” for similar reasons to JWTs. Ironically, the most widely used WebAuthn signature algorithm, ECDSA, is itself a Schnorr-ish scheme.
TLS also uses signatures for what is essentially an identification protocol, and similarly has had a range of bugs due to insufficient context binding information being included in the signed data. (SSL also uses signatures for verifying certificates, which is IMO a perfectly good use of the technology. Certificates are exactly a case of where you want to convert an interactive protocol into a non-interactive one. But then again we also do an interactive protocol (DNS) in that case anyway 🤷).
In short, an awful lot of uses of digital signatures are actually identification schemes of one form or another and would be better off using an actual identification scheme. But that doesn’t mean using something like Schnorr’s protocol! There are actually better alternatives that I’ll come back to at the end.
Special Soundness: fragility by design
Before I look at alternatives, I want to point out that pretty much all in-use signature schemes are extremely fragile in practice. The zero-knowledge security of Schnorr identification is based on it having a property called special soundness. Special soundness essentially says that if Alice accidentally reuses the same commitment (R) for two runs of the protocol, then any observer can recover her private key.This sounds like an incredibly fragile notion to build into your security protocol! If I accidentally reuse this random value then I leak my entire private key??! And in fact it is: such nonce-reuse bugs are extremely common in deployed signature systems, and have led to compromise of lots of private keys (eg Playstation 3, various Bitcoin wallets etc).
But despite its fragility, this notion of special soundness is crucial to the security of many signature systems. They are truly a cursed technology!
To solve this problem, some implementations and newer standards like EdDSA use deterministic commitments, which are based on a hash of the private key and the message. This ensures that the commitment will only ever be the same if the message is identical: preventing the private key from being recovered. Unfortunately, such schemes turned out to be more susceptible to fault injection attacks (a much less scalable or general attack vector), and so now there are “hedged” schemes that inject a bit of randomness back into the hash. It’s cursed turtles all the way down.
If your answer to this is to go back to good old RSA signatures, don’t be fooled. There are plenty of ways to blow your foot off using old faithful, but that’s for another post.
Did you want non-repudiation with that?
Another way that signatures cause issues is that they are too powerful for the job they are used for. You just wanted to authenticate that an email came from a legitimate server, but now you are providing irrefutable proof of the provenance of leaked private communications. Oops!Signatures are very much the hammer of cryptographic primitives. As well as authenticating a message, they also provide third-party verifiability and (part of) non-repudiation.
You don’t need to explicitly want anonymity or deniability to understand that these strong security properties can have damaging and unforeseen side-effects. Non-repudiation should never be the default in open systems.
I could go on. From the fact that there are basically zero acceptable post-quantum signature schemes (all way too large or too risky), to issues with non-canonical signatures and cofactors and on and on. The problems of signature schemes never seem to end.
What to use instead?
Ok, so if signatures are so bad, what can I use instead?Firstly, if you can get away with using a simple shared secret scheme like HMAC, then do so. In contrast to public key crypto, HMAC is possibly the most robust crypto primitive ever invented. You’d have to go really far out of your way to screw up HMAC. (I mean, there are timing attacks and that time that Bouncy Castle confused bits and bytes and used 16-bit HMAC keys, so still do pay attention a little bit…)
If you need public key crypto, then… still use HMAC. Use an authenticated KEM with X25519 to generate a shared secret and use that with HMAC to authenticate your message. This is essentially public key authenticated encryption without the actual encryption. (Some people mistakenly refer to such schemes as designated verifier signatures, but they are not).
Signatures are good for software/firmware updates and pretty terrible for everything else.
https://neilmadden.blog/2024/09/18/digital-signatures-and-how-to-avoid-them/
#authenticatedEncryption #cryptography #misuseResistance #signatures

Earlier this year, Cendyne published A Deep Dive into Ed25519 Signatures, which covered some of the different types of digital signature algorithms, but mostly delved into the Ed25519 algorithm. Truth in advertising.
This got me thinking, “Why isn’t there a better comparison of different elliptic curve signature algorithms available online?”

Most people just defer to SafeCurves, but it’s a little dated: We have complete addition formulas for Weierstrass curves now, but SafeCurves doesn’t reflect that.
For the purpose of simplicity, I’m not going to focus on a general treatment of Elliptic Curve Cryptography (ECC), which includes pairing-based cryptography, Elliptic-Curve Diffie-Hellman, and (arguably) isogeny cryptography.
Instead, I’m going to focus entirely on elliptic curve digital signature algorithms.
Note: The content of this post is a bit lower-level than most programmers ever need to be concerned with. If you’re a programmer and interested in learning cryptography, start here. If you’re looking for library recommendations, libsodium is a good safe default.
Compliance Rules Everything Around Me
If you have to meet some arbitrary compliance requirements (i.e. FIPS 140-3, CNSA, etc.), your decision is already made for you, and you shouldn’t waste your time reading blogs like this that will only get your hopes up about the options available to you.
Choose the option your compliance officer demands, and hope it’s good enough.

Art: LvJ
Elliptic Curves for Signature Algorithms
Let’s start with the same curve Cendyne analyzed: Ed25519.
Ed25519 (EdDSA, Curve25519)
Ed25519 is one of the two digital signature algorithms today that use the EdDSA algorithm framework. The other is Ed448, which targets a higher security level (224-bit vs 128-bit) but is also slower and uses SHAKE256 (which is overkill and not great for performance).
Ed25519 is a safe default choice for most applications where a digital signature is appropriate, for many reasons:
- Ed25519 uses deterministic nonces, which means you’re severely unlikely to ever reproduce the Sony ECDSA k-reuse bug in your system.
The deterministic nonce is calculated from the SHA512 hash of the secret key and message. Two invocations tocrypto_sign_ed25519()with the same message and secret key will produce the same signature, but the intermediate nonce value is never revealed to an attacker. - Ed25519 includes the public key in the data hashed to produce the signature (more specifically s from the (R,s) pair). This offers a property that ECDSA lacks: Exclusive Ownership. I’ve written about this property before.
Without Exclusive Ownership, it’s possible to create a single signature value that’s valid for multiple different (message, public key) pairs.
Years ago, there would have an additional list item: Ed25519 uses Edward Curves, which have complete addition formulas and are therefore safer to implement in constant-time than Weierstrass curves (i.e. the NIST curves). However, we now have complete addition formulas for Weierstrass curves, so this has become a moot point (assuming your implementation uses complete addition formulas).
Ed25519 targets the 128-bit security level.
Why Not Use Ed25519?
There is one minor pitfall of Ed25519 that makes it unsuitable for esoteric uses (say, Ring Signature Schemes or zero-knowledge proofs): Ed25519 is not a prime-order group; it has a cofactor h = 8. This detail famously created a double-spend vulnerability in all CryptoNote-based cryptocurrencies (including Monero).
For systems that want the security of Ed25519 and its various well-studied implementations, but still need a prime-order group for their protocol, cryptographers have developed the Ristretto Group to meet your needs.
If you’re working on embedded systems, the determinism inherent to EdDSA might be undesirable due to the possibility of fault attacks. You can use a hedged variant of Ed25519 to mitigate this risk.
Additionally, Ed25519 is not approved for many government applications, although it did make the latest draft revision of FIPS 186 in 2019. If you care about compliance (see above), you cannot use Ed25519. Yet.

Guidance for Ed25519
Unless legally prohibited, Ed25519 should be your default choice, unless you need a prime-order group. In that case, build your desired protocol atop Ristretto255.
If you’re not sure if you need a prime-order group, you probably don’t. It’s a specialized requirement for uncommon use cases (ring signatures, password authenticated key exchange protocols, zero-knowledge proofs, etc.).

The Bitcoin Curve (ECDSA, secp256k1)
Secp256k1 is a Koblitz curve, which is a special case of Weierstrass curves that are more performant when used in binary fields, of the form, 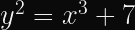
There is no specified reason why Bitcoin chose secp256k1 over another elliptic curve at the time of its inception, but we can speculate:
The author was a pseudonymous contributor to the Metzdowd mailing list for cypherpunks, and probably didn’t trust the NIST curves. Since Ed25519 didn’t exist at the time, the only obvious choice for a hipster elliptic curve parameter selection was to rely on the SECG recommendations, which specify the NIST and Koblitz curves. If you cross the NIST curves off the list, only the Koblitz curves remained.
Therefore, the selection of secp256k1 is likely an artefact of computer history and not a compelling reason to select secp256k1 in new designs. Please look elsewhere.

Secp256k1 targets the 128-bit security level.
Guidance for secp256k1
Don’t bother, there are better options. (i.e. Ed25519)
If you’re writing software for a cryptocurrency-related project, and you feel compelled to use secp256k1 for the sake of reducing your code footprint, please strongly consider the option of burning everything to the proverbial ground.

Art: Swizz
Cryptocurrency Aside, Why Avoid Secp256k1?
As we noted above, secp256k1 isn’t widely used outside of cryptocurrency.
As a direct consequence of this (as we’ll discuss in the NIST P-256 section), most cryptography libraries don’t offer optimized, side-channel-resistant implementations of secp256k1; even if they do offer optimized implementations of NIST P-256.
(Meanwhile, Ed25519 is designed to be side-channel and misuse-resistant, partly due to its Schnorr construction and constant-time ladder for scalar multiplication, so any library that implements Ed25519 is overwhelmingly likely to be constant-time.)
Therefore, any secp256k1 library for most programming languages that isn’t an FFI wrapper for libsecp256k1 will have worse performance than the other 256-bit curves.
https://twitter.com/bascule/status/1320183684935290882
Additionally, secp256k1 implementations are often a source of exploitable side-channels that permit attackers to pilfer your secret keys.
The previously linked article was about BouncyCastle’s implementation (which covers Java and .NET), but there’s still plenty of secp256k1 implementations that don’t FFI libsecp256k1.
From a quick Google Search:
- Python (uses EEA rather than Binary GCD for modular inverse)
- Go (uses Numbers, which weren’t designed for cryptography)
- PHP (uses GMP, which isn’t constant-time)
- JavaScript (calls here, which uses bn.js, which isn’t constant-time)
If you’re using secp256k1, and you’re not basing your choice on cybercash-interop, you’re playing with fire at the implementation and ecosystem levels–even if there are no security problems with the Koblitz curve itself.
You are much better off choosing any different curve than secp256k1 if you don’t have a Bitcoin/Ethereum/etc. interoperability requirement.

Art: LvJ
NIST P-256 (ECDSA, secp256r1)
NIST P-256 is the go-to curve to use with ECDSA in the modern era. Unlike Ed25519, P-256 uses a prime-order group, and is an approved algorithm to use in FIPS-validated modules.
Most cryptography libraries offer optimized assembly implementations of NIST P-256, which makes it less likely that your signing operations will leak timing information or become a significant performance bottleneck.
P-256 targets the 128-bit security level.
Why Not Use P-256?
Once upon a time, P-256 was riskier than Ed25519 (for signatures) and X25519 (for Diffie-Hellman), due to the incomplete addition formulas that led to timing-leaky implementations.
If you’re running old software, you may still be vulnerable to timing attacks that can recover your ECDSA secret key. However, there is a good chance that you’re on a modern and secure implementation in 2022, especially if you’re outsourcing this to OpenSSL or its derivatives.
ECDSA requires a secure randomness source to sign data. If you don’t have one available, and you sign anything, you’re coughing up your secret key to any attacker capable of observing multiple signatures.
Guidance for P-256
P-256 is an acceptable choice, especially if you’re forced to cope with FIPS and/or the CNSA suite requirements when using cryptography.
Of course, if you can get away with Ed25519, use Ed25519 instead.
If you use P-256, make sure you’re using it with SHA-256. Some implementations may default to something weaker (e.g. SHA-1).
If you’re also going to be performing ECDH with P-256, make sure you use compressed points. There used to be a patent; it died in 2018.
If you can afford it, make sure you use deterministic ECDSA (RFC 6979) or hedged signatures (if fault attacks are relevant to your threat model).

NIST P-384 (ECDSA, secp384r1)
NIST P-384 has a larger field than the curves we’ve previously examined, which allows P-384 to target the 192-bit security level. That’s the primary reason why anyone would choose P-384.
Naturally, elliptic curve security is more complicated than merely security against the Elliptic Curve Discrete Logarithm Problem (ECDLP).
P-384 is most often paired with SHA-384, which is the most widely used flavor of the SHA-2 family hash functions that isn’t susceptible to length-extension attacks. (There are also truncated SHA-512 variants specified later, but that’s also what SHA-384 is under-the-hood.)
If you’re aiming to build a “secure-by-default” tool for a system that the US government might one day become a customer of, with minimal cryptographic primitive choice, using NIST P-384 with SHA-384 makes for a reasonably minimalistic bundle.
Why Not Use P-384?
Unlike P-256, most P-384 implementations don’t use constant-time, optimized, and/or formally verified assembly code. (Notable counter-examples: AWS-LC and Go x/crypto.)
Like P-256, P-384 also requires a secure randomness source to sign data. If you aren’t providing one, expect your signing key to end up on fail0verflow one day.
Guidance for P-384
If you use P-384, make sure you’re using it with SHA-384.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

NIST P-521 (ECDSA, secp521r1)
Biggest curve is best curve! — the clueless
https://www.youtube.com/watch?v=i_APoSfCYwU
Systems that choose P-521 often have an interesting threat model, even though said threat model is rarely formally specified.
It’s overwhelmingly likely that what eventually breaks the 256-bit elliptic curves will also break P-521 in short order: Cryptography Relevant Quantum Computers.
The only thing P-521 does against CRQCs that P-256 doesn’t is require more quantum memory. If you’re worried about QRQCs, you might want to look into hybrid post-quantum signature schemes.
If you’re choosing P-521 in your designs, you’re basically saying, “I want to have 256 bits of asymmetric cryptographic security, come hell or high water!” even though the 128-bit security level is likely just fine for your actual threats.
Aside: P-521 and 512-bit ECC Security
P-521 is not a typo, although people sometimes think it is. P-521 uses the Mersenne prime 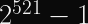
This has led to an unfortunate trend in cryptography media to map ECC key sizes to symmetric security levels that misleads people as to the relationship between the two. For example:
Regrettably, this is misleading, because plotting the ECC Key Size versus equivalent Symmetric Security isn’t a how ECDLP security works. The ratio of the exponents involved is totally linear; it doesn’t suddenly increase beyond 384-bit curves for a mysterious mathematical reason.
- 256-bit Curves target the 128-bit security level
- 384-bit Curves target the 192-bit security level
- 512-bit Curves target the 256-bit security level
- 521-bit Curves actually target the 260-bit security level, but that meets or exceeds the 256-bit security level, so that’s how the standards are interpreted
The reason for this boils down entirely to the best attack against the Elliptic Curve Discrete Logarithm Problem: Pollard’s Rho, which recovers the secret key from an 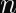
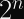
Taking the square root of a number is the same as halving its exponent, so the security level is half: 
Takeaway: If someone tells you that you need a 521-bit curve to meet the 256-bit security level, they are mistaken and it’s not their fault.

Why Not Use P-521?
It’s slow. Much slower than P-256 and Ed25519. Modestly slower than P-384.
Unlike P-384, you’re less likely to find an optimized, constant-time P-521 implementation.
Guidance for P-521
First, make a concerted effort to figure out the motivation for P-521 in your designs. Chances are, someone is putting too much emphasis on the wrong things for security.
If you use P-521, make sure you’re using it with SHA-512.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

Ed448 (EdDSA, Curve448)
Ed448 is the P-521 of the Edwards curves: It mostly exists to give standards committees a psychological comfort for the unlikely event that 256-bit ECC is desperately broken but ECC larger than 384 bits is somehow still safe.
https://twitter.com/dchest/status/703017144053833728
The very concept of having multiple “security levels” for raw cryptography primitives is mostly an artefact of the historical military roots of cryptography, rather than a serious consideration in the modern world.
Unfortunately, this leads to implementations that prioritize runtime algorithm selection negotiation, which maximizes the risk of protocol-level vulnerabilities. See also: JWT.
Ed448 was specified to use SHAKE256, which is a needlessly conservative decision which leads to an unnecessary performance bottleneck.
Why Not Use Ed448?
Aside from the performance hit mentioned previously, there’s no compelling reason to avoid Ed448 that isn’t also true of either Ed25519 or P-384.
Guidance for Ed448
If you want more speed, go with Ed25519. In addition to being faster, Ed25519 is also very widely supported.
If you need a prime-order field, use Decaf with Ed448 or consider P-384.
The Brainpool Curves
The main motivation for the Brainpool curves is that the NIST curves were not generated in a “verifiable pseudo-random way”.
The only reasons you’d ever want to support the Brainpool curves include:
- You think the NIST curves are somehow backdoored by the NSA
- You don’t appreciate small attack surfaces in cryptography libraries
- The German government told you to (see: compliance)
Most of the advice for the NIST Curves at each security level can be copy/pasted for the Brainpool curves, with one important caveat:
When considering real-world implementations, Brainpool curves are more likely to use the general purpose Big Number procedures (which aren’t always constant-time), rather than optimized assembly code, than the NIST curves are.
Therefore, my general guidance for the Brainpool curves is simply:
- Proceed at your own peril
- Consider hiring a cryptography engineer to study the implementation you’re relying on, especially with regard to timing attacks

Art: LvJ
Re-Examining the SafeCurves Criteria
Here’s a 2022 refresh of the SafeCurves criteria for all of the curves considered by this blog post.
| SafeCurve Criteria | Relevance to the Curves Listed Above |
|---|---|
| Fields | All relevant curves satisfy the requirements |
| Equations | All relevant curves satisfy the requirements |
| Base Points | All relevant curves satisfy the requirements |
| Rho | All relevant curves satisfy the requirements |
| Transfers | All relevant curves satisfy the requirements |
| Discriminants | Only secp256k1 doesn’t satisfy the requirements (out of the curves listed in this blog post) |
| Rigidity | The NIST curves do not meet this requirement. If you care about whether or not the standards were manipulated to insert a backdoor, rigidity matters to you. Otherwise, it’s not a deal-breaker. |
| Ladders | While a Montgomery ladder is beneficial for speed and implementation security, it isn’t strictly speaking required. This is an icing-on-the-cake consideration. |
| Twists | The only curve listed above that doesn’t meet the requirement is the 256-bit Brainpool curve (brainpoolp256t1). |
| Completeness | All relevant curves satisfy the requirements, as of 2015. SafeCurves is out of date here. |
| Indistinguishability | All relevant curves satisfy the requirements, as of 2014. |
SafeCurves continues to be a useful resource, especially if you stray from the guidance on this page.
For example: You wouldn’t want to use pairing-friendly curves for general purpose ECC digital signatures, because they’re suitable for specialized problems. SafeCurves correctly recommends not using BN(2,254).
However, SafeCurves is showing its age in 2022. BN curves still end up in digital signature protocol standards even though BLS-12-381 is clearly a better choice.
The Internet would benefit greatly for an updated SafeCurves that focuses on newer elliptic curve algorithms.

TL;DR
Ed25519 is great. NIST P-256 and P-384 are okay (with caveats). Anything else is questionable, and their parameter selection should come with a clear justification.
https://soatok.blog/2022/05/19/guidance-for-choosing-an-elliptic-curve-signature-algorithm-in-2022/
#asymmetricCryptography #BrainpoolCurves #cryptography #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #ellipticCurveCryptography #P256 #P384 #P521 #secp256k1 #secp256r1 #secp384r1 #secp521r1 #SecurityGuidance
A question I get asked frequently is, “How did you learn cryptography?”I could certainly tell everyone my history as a self-taught programmer who discovered cryptography when, after my website for my indie game projects kept getting hacked, I was introduced to cryptographic hash functions… but I suspect the question folks want answered is, “How would you recommend I learn cryptography?” rather than my cautionary tale about poorly-implemented password hash being a gateway bug.
The Traditional Ways to Learn
There are two traditional ways to learn cryptography.If you want a book to augment your journey in either traditional path, I recommend Serious Cryptography by Jean-Philippe Aumasson.
Academic Cryptography
The traditional academic way to learn cryptography involves a lot of self-study about number theory, linear algebra, discrete mathematics, probability, permutations, and field theory.You’d typically start off with classical ciphers (Caesar, etc.) then work your way through the history of ciphers until you finally reach an introduction to the math underpinning RSA and Diffie-Hellman, and maybe taught about Schneier’s Law and cautioned to only use AES and SHA-2… and then you’re left to your own devices unless you pursue a degree in cryptography.
The end result of people carelessly exploring this path is a lot of designs like Telegram’s MTProto that do stupid things with exotic block cipher modes and misusing vanilla cryptographic hash functions as message authentication codes; often with textbook a.k.a. unpadded RSA, AES in ECB, CBC, or some rarely-used mode that the author had to write custom code to handle (using ECB mode under the hood), and (until recently) SHA-1.
People who decide to pursue cryptography as a serious academic discipline will not make these mistakes. They’re far too apt for the common mistakes. Instead, they run the risk of spending years involved in esoteric research about homomorphic encryption, cryptographic pairings, and other cool stuff that might not see real world deployment (outside of novel cryptocurrency hobby projects) for five or more years.
That is to say: Academia is a valid path to pursue, but it’s not for everyone.
If you want to explore this path, Cryptography I by Dan Boneh is a great starting point.
Security Industry-Driven Cryptography
The other traditional way to learn cryptography is to break existing cryptography implementations. This isn’t always as difficult as it may sound: Reverse engineering video games to defeat anti-cheat protections has led several of my friends into learning about cryptography.For security-minded folks, the best place to start is the CryptoPals challenges. Another alternative is CryptoHack.
There are also plenty of CTF events all year around, but they’re rarely a good cryptography learning exercise above what CryptoPals offers. (Though there are notable exceptions.)
A Practical Approach to Learning Cryptography
Art by Kyume.
If you’re coming from a computer programming background and want to learn cryptography, the traditional approaches carry the risk of Reasoning By Lego.
Instead, the approach I recommend is to start gaining experience with the safest, highest-level libraries and then slowly working your way down into the details.
This approach has two benefits:
- If you have to implement something while you’re still learning, your knowledge and experience is stilted towards “use something safe and secure” not “hack together something with Blowfish in ECB mode and MD5 because they’re familiar”.
- You can let your own curiosity guide your education rather than follow someone else’s study guide.
To illustrate what this looks like, here’s how a JavaScript developer might approach learning cryptography, starting from the most easy-mode library and drilling down into specifics.
Super Easy Mode: DholeCrypto
Disclaimer: This is my project.Dhole Crypto is an open source library, implemented in JavaScript and PHP and powered by libsodium, that tries to make security as easy as possible.
I designed Dhole Crypto for securing my own projects without increasing the cognitive load of anyone reviewing my code.
If you’re an experienced programmer, you should be able to successfully use Dhole Crypto in a Node.js/PHP project. If it does not come easy, that is a bug that should be fixed immediately.
Easy Mode: Libsodium
Using libsodium is slightly more involved than Dhole Crypto: Now you have to know what a nonce is, and take care to manage them carefully.Advantage: Your code will be faster than if you used Dhole Crypto.
Libsodium is still pretty easy. If you use this cheat sheet, you can implement something secure without much effort. If you deviate from the cheat sheet, pay careful attention to the documentation.
If you’re writing system software (i.e. programming in C), libsodium is an incredibly easy-to-use library.
Moderate Difficulty: Implementing Protocols
Let’s say you’re working on a project where libsodium is overkill, and you only need a few cryptography primitives and constructions (e.g. XChaCha20-Poly1305). A good example: In-browser JavaScript.Instead of forcing your users to download the entire Sodium library, you might opt to implement a compatible construction using JavaScript implementations of these primitives.
Since you have trusted implementations to test your construction against, this should be a comparatively low-risk effort (assuming the primitive implementations are also secure), but it’s not one that should be undertaken without all of the prior experience.
Note: At this stage you are not implementing the primitives, just using them.
Hard Difficulty: Designing Protocols and Constructions
Repeat after me: “I will not roll my own crypto before I’m ready.” Art by AtlasInu.
To distinguish: TLS and Noise are protocols. AES-GCM and XChaCha20-Poly1305 are constructions.
Once you’ve implemented protocols and constructions, the next step in your self-education is to design new ones.
Maybe you want to combine XChaCha20 with a MAC based on the BLAKE3 hash function, with some sort of SIV to make the whole shebang nonce-misuse resistant?
You wouldn’t want to dive headfirst into cryptography protocol/construction design without all of the prior experience.
Very Hard Mode: Implementing Cryptographic Primitives
It’s not so much that cryptography primitives are hard to implement. You could fit RC4 in a tweet before they raised the character limit to 280. (Don’t use RC4 though!)The hard part is that they’re hard to implement securely. See also: LadderLeak.
Usually when you get to this stage in your education, you will have also picked up one or both of the traditional paths to augment your understanding. If not, you really should.
Nightmare Mode: Designing Cryptography Primitives
A lot of people like to dive straight into this stage early in their education. This usually ends in tears.If you’ve mastered every step in my prescribed outline and pursued both of the traditional paths to the point that you have a novel published attack in a peer-reviewed journal (and mirrored on ePrint), then you’re probably ready for this stage.
Bonus: If you’re a furry and you become a cryptography expert, you can call yourself a cryptografur. If you had no other reason to learn cryptography, do it just for pun!
Header art by circuitslime.
https://soatok.blog/2020/06/10/how-to-learn-cryptography-as-a-programmer/
#cryptography #education #programming #Technology

Did you know that, in the Furry Fandom, the most popular choice in species for one’s fursona is actually a hybrid?
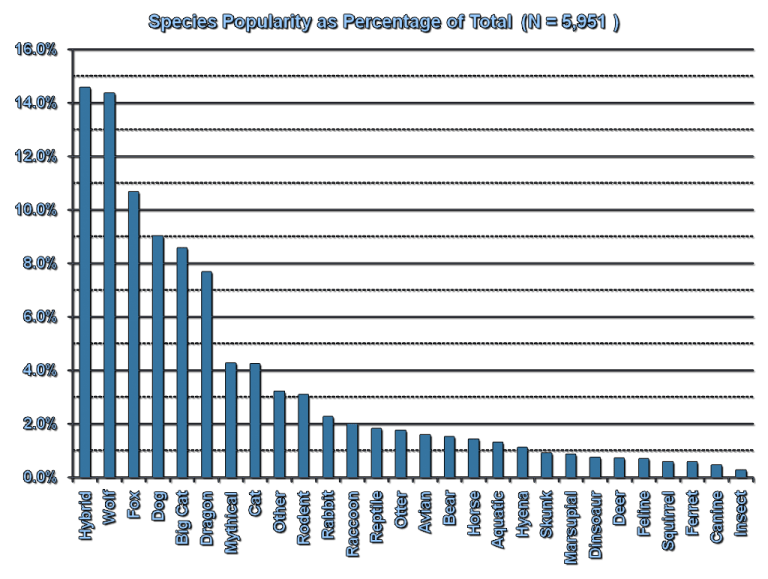
Of course, we’re not talking about that kind of hybrid today. I just thought it was an amusing coincidence.

Nor are we talking about what comes to mind for engineers accustomed to classical cryptography when you say Hybrid.
(Such engineers typically envision some combination of asymmetric key encapsulation with symmetric encryption; because too many people encrypt with RSA directly and the sane approach is often described as a Hybrid Cryptosystem in the literature.)
Rather, Hybrid Cryptography in today’s context refers to:
Cryptography systems that use a post-quantum cryptography algorithm, combined with one of the algorithms deployed today that aren’t resistant to quantum computers.
If you need to differentiate the two, PQ-Hybrid might be a better designation.
Why Hybrid Cryptosystems?
At some point in the future (years or decades from now), humanity may build a practical quantum computer. This will be a complete disaster for all of the cryptography deployed on the Internet today.
In response to this distant existential threat, cryptographers have been hard at work designing and attacking algorithms that remain secure even when quantum computers arrive. These algorithms are classified as post-quantum cryptography (mostly to distinguish it from techniques that uses quantum computers to facilitate cryptography rather than attack it, which is “quantum cryptography” and not really worth our time talking about). Post-quantum cryptography is often abbreviated as “PQ Crypto” or “PQC”.
However, a lot of the post-quantum cryptography designs are relatively new or comparatively less studied than their classical (pre-quantum) counterparts. Several of the Round 1 candidates to NIST’s post quantum cryptography project were broken immediately (PDF). Exploit code referenced in PDF duplicated below.:
#!/usr/bin/env python3import binascii, structdef recover_bit(ct, bit): assert bit < len(ct) // 4000 ts = [struct.unpack('BB', ct[i:i+2]) for i in range(4000*bit, 4000*(bit+1), 2)] xs, ys = [a for a, b in ts if b == 1], [a for a, b in ts if b == 2] return sum(xs) / len(xs) >= sum(ys) / len(ys)def decrypt(ct): res = sum(recover_bit(ct, b) << b for b in range(len(ct) // 4000)) return int.to_bytes(res, len(ct) // 4000 // 8, 'little')kat = 0for l in open('KAT_GuessAgain/GuessAgainEncryptKAT_2000.rsp'): if l.startswith('msg = '): # only used for verifying the recovered plaintext. msg = binascii.unhexlify(l[len('msg = '):].strip()) elif l.startswith('c = '): ct = binascii.unhexlify(l[len('c = '):].strip()) print('{}attacking known-answer test #{}'.format('\n' * (kat > 0), kat)) print('correct plaintext: {}'.format(binascii.hexlify(msg).decode())) plain = decrypt(ct) print('recovered plaintext: {} ({})'.format(binascii.hexlify(plain).decode(), plain == msg)) kat += 1
More pertinent to our discussions: Rainbow, which was one of the Round 3 Finalists for post-quantum digital signature algorithms, was discovered in 2020 to be much easier to attack than previously thought. Specifically, for the third round parameters, the attack cost was reduced by a factor of 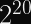
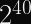
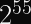
That security reduction is just a tad bit more concerning than a Round 1 candidate being totally broken, since NIST had concluded by then that Rainbow was a good signature algorithm until that attack was discovered. Maybe there are similar attacks just waiting to be found?
Given that new cryptography is accompanied by less confidence than incumbent cryptography, hybrid designs are an excellent way to mitigate the risk of attack advancements in post-quantum cryptography:
If the security of your system requires breaking the cryptography used today AND breaking one of the new-fangled designs, you’ll always be at least as secure as the stronger algorithm.

Why Is Hybrid Cryptography Controversial?
Despite the risks of greenfield cryptographic algorithms, the NSA has begun recommending a strictly-PQ approach to cryptography and have explicitly stated that they will not require hybrid designs.
Another pushback on hybrid cryptography comes from Uri Blumenthal of MIT’s Lincoln Labs on the IETF CFRG mailing list (the acronym CRQC expands to “Cryptographically-Relevant Quantum Computer”):
Here are the possibilities and their relation to the usefulness of the Hybrid approach.1. CRQC arrived, Classic hold against classic attacks, PQ algorithms hold – Hybrid is useless.
2. CRQC arrived, Classic hold against classic attacks, PQ algorithms fail – Hybrid is useless.
3. CRQC arrived, Classic broken against classic attacks, PQ algorithms hold – Hybrid is useless.
4. CRQC arrived, Classic hold against classic attacks, PQ algorithms broken – Hybrid useless.
5. CRQC doesn’t arrive, Classic hold against classic attacks, PQ algorithms hold – Hybrid is useless.
6. CRQC doesn’t arrive, Classic hold against classic attacks, PQ algorithms broken – Hybrid helps.
7. CRQC doesn’t arrive, Classic broken against classic attacks, PQ algorithms hold – Hybrid is useless.
8. CRQC doesn’t arrive, Classic broken against classic attacks, PQ algorithms broken – Hybrid is useless.
Uri Blumenthal, IETF CFRG mailing list, December 2021 (link)
Why Hybrid Is Actually A Damn Good Idea

Uri’s risk analysis is, of course, flawed. And I’m not the first to disagree with him.
First, Uri’s framing sort of implies that each of the 8 possible outputs of these 3 boolean variables are relatively equally likely outcomes.
It’s very tempting to look at this and think, “Wow, that’s a lot of work for something that only helps in 12.5% of possible outcomes!” Uri didn’t explicitly state this assumption, and he might not even believe that, but it is a cognitive trap that emerges in the structure of his argument, so watch your step.
Second, for many candidate algorithms, we’re already in scenario 6 that Uri outlined! It’s not some hypothetical future, it’s the present state of affairs.
To wit: The advances in cryptanalysis on Rainbow don’t totally break it in a practical sense, but they do reduce the security by a devastating margin (which will require significantly larger parameter sets and performance penalties to remedy).
For many post-quantum algorithms, we’re still uncertain about which scenario is most relevant. But since PQ algorithms are being successfully attacked and a quantum computer still hasn’t arrived, and classical algorithms are still holding up fine, it’s very clear that “hybrid helps” is the world we most likely inhabit today, and likely will for many years (until the existence of quantum computers is finally settled).
Finally, even in other scenarios (which are more relevant for other post-quantum algorithms), hybrid doesn’t significantly hurt security. It does carry a minor cost to bandwidth and performance, and it does mean having a larger codebase to review when compared with jettisoning the algorithms we use today, but I’d argue that the existing code is relatively low risk compared to new code.
From what I’ve read, the NSA didn’t make as strong an argument as Uri; they said hybrid would not be required, but didn’t go so far as to attack it.
Hybrid cryptography is a long-term bet that will protect the most users from cryptanalytic advancements, contrasted with strictly-PQ and no-PQ approaches.
Why The Hybrid Controversy Remains Unsettled
Even if we can all agree that hybrid is the way to go, there’s still significant disagreement on exactly how to do it.
Hybrid KEMs
There are two schools of thought on hybrid Key Encapsulation Mechanisms (KEMs):
- Wrap the post-quantum KEM in the encrypted channel created by the classical KEM.
- Use both the post-quantum KEM and classical KEM as inputs to a secure KDF, then use a single encrypted channel secured by both.
The first option (layered) has the benefit of making migrations smoother. You can begin with classical cryptography (i.e. ECDHE for TLS ciphersuites), which is what most systems online support today. Then you can do your post-quantum cryptography inside the existing channel to create a post-quantum-secure channel. This also lends toward opportunistic upgrades (which might not be a good idea).
The second option (composite) has the benefit of making the security of your protocol all-or-nothing: You cannot attack the weak now and the strong part later. The session keys you’ll derive require attacking both algorithms in order to get access to the plaintext. Additionally, you only need a single layer. The complexity lies entirely within the handshake, instead of every packet.
Personally, I think composite is a better option for security than layered.
Hybrid Signatures
There are, additionally, two different schools of thought on hybrid digital signature algorithms. However, the difference is more subtle than with KEMs.
- Require separate classical signatures and post-quantum signatures.
- Specify a composite mode that combines the two together and treat it as a distinct algorithm.
To better illustrate what this looks like, I outlined what a composite hybrid digital signature algorithm could look like on the CFRG mailing list:
primary_seed := randombytes_buf(64) // store thised25519_seed := hash_sha512256(PREFIX_CLASSICAL || primary_seed)pq_seed := hash_sha512256(PREFIX_POSTQUANTUM || primary_seed)ed25519_keypair := crypto_sign_seed_keypair(ed25519_seed)pq_keypair := pqcrypto_sign_seed_keypair(pq_seed)
Your composite public key would be your Ed25519 public key, followed by your post-quantum public key. Since Ed25519 public keys are always 32 bytes, this is easy to implement securely.
Every composite signature would be an Ed25519 signature concatenated with the post-quantum signature. Since Ed25519 signatures are always 64 bytes, this leads to a predictable signature size relative to the post-quantum signature.
The main motivation for preferring a composite hybrid signature over a detached hybrid signature is to push the hybridization of cryptography lower in the stack so developers don’t have to think about these details. They just select HYBRIDSIG1 or HYBRIDSIG2 in their ciphersuite configuration, and cryptographers get to decide what that means.
TL;DR
Hybrid designs of post-quantum crypto are good, and I think composite hybrid designs make the most sense for both KEMs and signatures.
https://soatok.blog/2022/01/27/the-controversy-surrounding-hybrid-cryptography/
#asymmetricCryptography #classicalCryptography #cryptography #digitalSignatureAlgorithm #hybridCryptography #hybridDesigns #KEM #keyEncapsulationMechanism #NISTPostQuantumCryptographyProject #NISTPQC #postQuantumCryptography
Let me state up front that, while we’re going to be talking about an open source project that was recently submitted to Hacker News’s “Show HN” section, the intent of this post is not at all to shame the developer who tried their damnedest to do the right thing. They’re the victim, not the culprit.RSA, Ya Don’t Say
Earlier this week, an HN user shared their open source fork of a Facebook’s messenger client, with added encryption. Their motivation was, as stated in the readme:It is known that Facebook scans your messages. If you need to keep using Facebook messenger but care about privacy, Zuccnet might help.It’s pretty simple: you and your friend have Zuccnet installed. Your friend gives you their Zuccnet public key. Then, when you send a message to your friend on Zuccnet, your message is encrypted on your machine before it is sent across Facebook to your friend. Then, your friend’s Zuccnet decrypts the message. Facebook never sees the content of your message.
I’m not a security person and there’s probably some stuff I’ve missed – any contributions are very welcome! This is very beta, don’t take it too seriously.
From Zuccnet’s very humble README.
So far, so good. Facebook is abysmal for privacy, so trying to take matters into your own hands to encrypt data so Facebook can’t see what you’re talking about is, in spirit, a wonderful idea.
(Art by Khia.)
However, there is a problem with the execution of this idea. And this isn’t a problem unique to Zuccnet. Several times per year, I come across some well-meaning software project that makes the same mistake: Encrypting messages with RSA directly is bad.
From the Zuccnet source code:
const encryptMessage = (message, recipientPublicKey) => { const encryptedMessage = crypto.publicEncrypt( { key: recipientPublicKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(message), ); return encryptedMessage.toString("base64");};/** * * @param {String} encryptedMessage - base64 encoded string */const decryptMessage = encryptedMessage => { const encryptedMessageBuffer = Buffer.from(encryptedMessage, "base64"); const { privateKey } = getOrCreateZuccnetKeyPair(); const message = crypto.privateDecrypt( { key: privateKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(encryptedMessageBuffer), );};
To the Zuccnet author’s credit, they’re using OAEP padding, not PKCS#1 v1.5 padding. This means their code isn’t vulnerable to Bleichenbacher’s 1998 padding oracle attack (n.b. most of the RSA code I encounter in the wild is vulnerable to this attack).
However, there are other problems with this code:
- If you try to encrypt a message longer than 256 bytes with a 2048-bit RSA public key, it will fail. (Bytes matter here, not characters, even for English speakers–because emoji.)
- This design (encrypting with a static RSA public key per recipient) completely lacks forward secrecy. This is the same reason that PGP encryption sucks (or, at least, one of the reasons PGP sucks).
There are many ways to work around the first limitation.
Some cryptography libraries let you treat RSA as a block cipher in ECB mode and encrypt each chunk independently. This is an incredibly stupid API deign choice: It’s slow (asymmetric cryptography operations are on the order of tens-to-hundreds-of-thousands times slower than symmetric cryptography) and you can drop/reorder/replay blocks, since ECB mode provides no semantic security.
I have strong opinions about cryptographic library design.
(Art by Swizz.)A much better strategy is to encrypt the data with a symmetric key, then encrypt that key with RSA. (See the end of the post for special treatment options that are especially helpful for RSA with PKCS#1 v1.5 padding.)
Working around the second problem usually requires an Authenticated Key Exchange (AKE), similar to what I covered in my Guide to End-to-End Encryption. Working around this second problem also solves the first problem, so it’s usually better to just implement a forward-secret key exchange protocol than try to make RSA secure.
(You can get forward secrecy without an AKE, by regularly rotating keys, but AKEs make forward secrecy automatic and on-by-default without forcing humans to make a decision to rotate a credential– something most people don’t do unless they have to. AKEs trade user experience complexity for protocol complexity–and this trade-off is almost universally worth taking.)
Although AKEs are extremely useful, they’re a bit complex for most software developers to pick up without prior cryptography experience. (If they were easier, after all, there wouldn’t be so much software that encrypts messages directly with RSA in the first place.)
Note: RSA itself isn’t the reason that this lacks forward secrecy. The problem is how RSA is used.
Recommendations
For Developers
First, consider not using RSA. Hell, while you’re at it, don’t write any cryptography code that you don’t have to.Libsodium (which you should use) does most of this for you, and can easily be turned into an AKE comparable to the one Signal uses. The less cryptography code you have to write, the less can go catastrophically wrong–especially in production systems.
If jettisoning RSA from your designs is a non-starter, you should at least consider taking the Dhole Moments Pledge for Software Developers:
I will not encrypt messages directly with RSA, or any other asymmetric primitive.Simple enough, right?
Instead, if you find yourself needing to encrypt a message with RSA, remind yourself that RSA is for encrypting symmetric keys, not messages. And then plan your protocol design accordingly.Also, I’m pretty sure RSA isn’t random-key robust. Ask your favorite cryptographer if it matters for whatever you’re building.
(But seriously, you’re better off not using RSA at all.)
For Cryptography Libraries
Let’s ask ourselves, “Why are we forcing developers to know or even care about these details?”Libsodium doesn’t encumber developers with unnecessary decisions like this. Why does the crypto module built into JavaScript? Why does the crypto module built into most programming languages that offer one, for that matter? (Go is a notable exception here, because their security team is awesome and forward-thinking.)
In my opinion, we should stop shipping cryptography interfaces that…
- Mix symmetric and asymmetric cryptography in the same API
- Allow developers to encrypt directly with asymmetric primitives
- Force developers to manage their own nonces/initialization vectors
- Allow public/private keys to easily get confused (e.g. lack of type safety)
For example: Dhole Crypto is close to my ideal for general-purpose encryption.
Addendum: Securing RSA with PKCS#1 v1.5
Update: Neil Madden informs me that what I wrote here is actually very similar to a standard construction called RSA-KEM. You should use RSA-KEM instead of what I’ve sketched out, since that’s better studied by cryptographers.(I’ve removed the original sketch below, to prevent accidental misuse.)
https://soatok.blog/2021/01/20/please-stop-encrypting-with-rsa-directly/
#asymmetricCryptography #cryptography #RSA #SecurityGuidance #symmetricCryptography

Let me state up front that, while we’re going to be talking about an open source project that was recently submitted to Hacker News’s “Show HN” section, the intent of this post is not at all to shame the developer who tried their damnedest to do the right thing. They’re the victim, not the culprit.
RSA, Ya Don’t Say
Earlier this week, an HN user shared their open source fork of a Facebook’s messenger client, with added encryption. Their motivation was, as stated in the readme:
It is known that Facebook scans your messages. If you need to keep using Facebook messenger but care about privacy, Zuccnet might help.It’s pretty simple: you and your friend have Zuccnet installed. Your friend gives you their Zuccnet public key. Then, when you send a message to your friend on Zuccnet, your message is encrypted on your machine before it is sent across Facebook to your friend. Then, your friend’s Zuccnet decrypts the message. Facebook never sees the content of your message.
I’m not a security person and there’s probably some stuff I’ve missed – any contributions are very welcome! This is very beta, don’t take it too seriously.
From Zuccnet’s very humble README.
So far, so good. Facebook is abysmal for privacy, so trying to take matters into your own hands to encrypt data so Facebook can’t see what you’re talking about is, in spirit, a wonderful idea.

However, there is a problem with the execution of this idea. And this isn’t a problem unique to Zuccnet. Several times per year, I come across some well-meaning software project that makes the same mistake: Encrypting messages with RSA directly is bad.
From the Zuccnet source code:
const encryptMessage = (message, recipientPublicKey) => { const encryptedMessage = crypto.publicEncrypt( { key: recipientPublicKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(message), ); return encryptedMessage.toString("base64");};/** * * @param {String} encryptedMessage - base64 encoded string */const decryptMessage = encryptedMessage => { const encryptedMessageBuffer = Buffer.from(encryptedMessage, "base64"); const { privateKey } = getOrCreateZuccnetKeyPair(); const message = crypto.privateDecrypt( { key: privateKey, padding: crypto.constants.RSA_PKCS1_OAEP_PADDING, oaepHash: "sha256", }, Buffer.from(encryptedMessageBuffer), );};
To the Zuccnet author’s credit, they’re using OAEP padding, not PKCS#1 v1.5 padding. This means their code isn’t vulnerable to Bleichenbacher’s 1998 padding oracle attack (n.b. most of the RSA code I encounter in the wild is vulnerable to this attack).
However, there are other problems with this code:
- If you try to encrypt a message longer than 256 bytes with a 2048-bit RSA public key, it will fail. (Bytes matter here, not characters, even for English speakers–because emoji.)
- This design (encrypting with a static RSA public key per recipient) completely lacks forward secrecy. This is the same reason that PGP encryption sucks (or, at least, one of the reasons PGP sucks).
There are many ways to work around the first limitation.
Some cryptography libraries let you treat RSA as a block cipher in ECB mode and encrypt each chunk independently. This is an incredibly stupid API deign choice: It’s slow (asymmetric cryptography operations are on the order of tens-to-hundreds-of-thousands times slower than symmetric cryptography) and you can drop/reorder/replay blocks, since ECB mode provides no semantic security.

(Art by Swizz.)
A much better strategy is to encrypt the data with a symmetric key, then encrypt that key with RSA. (See the end of the post for special treatment options that are especially helpful for RSA with PKCS#1 v1.5 padding.)
Working around the second problem usually requires an Authenticated Key Exchange (AKE), similar to what I covered in my Guide to End-to-End Encryption. Working around this second problem also solves the first problem, so it’s usually better to just implement a forward-secret key exchange protocol than try to make RSA secure.
(You can get forward secrecy without an AKE, by regularly rotating keys, but AKEs make forward secrecy automatic and on-by-default without forcing humans to make a decision to rotate a credential– something most people don’t do unless they have to. AKEs trade user experience complexity for protocol complexity–and this trade-off is almost universally worth taking.)
Although AKEs are extremely useful, they’re a bit complex for most software developers to pick up without prior cryptography experience. (If they were easier, after all, there wouldn’t be so much software that encrypts messages directly with RSA in the first place.)
Note: RSA itself isn’t the reason that this lacks forward secrecy. The problem is how RSA is used.
Recommendations
For Developers
First, consider not using RSA. Hell, while you’re at it, don’t write any cryptography code that you don’t have to.
Libsodium (which you should use) does most of this for you, and can easily be turned into an AKE comparable to the one Signal uses. The less cryptography code you have to write, the less can go catastrophically wrong–especially in production systems.
If jettisoning RSA from your designs is a non-starter, you should at least consider taking the Dhole Moments Pledge for Software Developers:
I will not encrypt messages directly with RSA, or any other asymmetric primitive.Simple enough, right?
Instead, if you find yourself needing to encrypt a message with RSA, remind yourself that RSA is for encrypting symmetric keys, not messages. And then plan your protocol design accordingly.
Also, I’m pretty sure RSA isn’t random-key robust. Ask your favorite cryptographer if it matters for whatever you’re building.
(But seriously, you’re better off not using RSA at all.)
For Cryptography Libraries
Let’s ask ourselves, “Why are we forcing developers to know or even care about these details?”
Libsodium doesn’t encumber developers with unnecessary decisions like this. Why does the crypto module built into JavaScript? Why does the crypto module built into most programming languages that offer one, for that matter? (Go is a notable exception here, because their security team is awesome and forward-thinking.)
In my opinion, we should stop shipping cryptography interfaces that…
- Mix symmetric and asymmetric cryptography in the same API
- Allow developers to encrypt directly with asymmetric primitives
- Force developers to manage their own nonces/initialization vectors
- Allow public/private keys to easily get confused (e.g. lack of type safety)
For example: Dhole Crypto is close to my ideal for general-purpose encryption.
Addendum: Securing RSA with PKCS#1 v1.5
Update: Neil Madden informs me that what I wrote here is actually very similar to a standard construction called RSA-KEM. You should use RSA-KEM instead of what I’ve sketched out, since that’s better studied by cryptographers.
(I’ve removed the original sketch below, to prevent accidental misuse.)
https://soatok.blog/2021/01/20/please-stop-encrypting-with-rsa-directly/
#asymmetricCryptography #cryptography #RSA #SecurityGuidance #symmetricCryptography
Governments are back on their anti-encryption bullshit again.Between the U.S. Senate’s “EARN IT” Act, the E.U.’s slew of anti-encryption proposals, and Australia’s new anti-encryption law, it’s become clear that the authoritarians in office view online privacy as a threat to their existence.
Normally, when the governments increase their anti-privacy sabre-rattling, technologists start talking more loudly about Tor, Signal, and other privacy technologies (usually only to be drowned out by paranoid people who think Tor and Signal are government backdoors or something stupid; conspiracy theories ruin everything!).
I’m not going to do that.
Instead, I’m going to show you how to add end-to-end encryption to any communication software you’re developing. (Hopefully, I’ll avoid making any bizarre design decisions along the way.)
But first, some important disclaimers:
- Yes, you should absolutely do this. I don’t care how banal your thing is; if you expect people to use it to communicate with each other, you should make it so that you can never decrypt their communications.
- You should absolutely NOT bill the thing you’re developing as an alternative to Signal or WhatsApp.
- The goal of doing this is to increase the amount of end-to-end encryption deployed on the Internet that the service operator cannot decrypt (even if compelled by court order) and make E2EE normalized. The goal is NOT to compete with highly specialized and peer-reviewed privacy technology.
- I am not a lawyer, I’m some furry who works in cryptography. The contents of this blog post is not legal advice, nor is it endorsed by any company or organization. Ask the EFF for legal questions.
The organization of this blog post is as follows: First, I’ll explain how to encrypt and decrypt data between users, assuming you have a key. Next, I’ll explain how to build an authenticated key exchange and a ratcheting protocol to determine the keys used in the first step. Afterwards, I’ll explore techniques for binding authentication keys to identities and managing trust. Finally, I’ll discuss strategies for making it impractical to ever backdoor your software (and impossible to silently backdoor it), just to piss the creeps and tyrants of the world off even more.
You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing.
(Art by Kyume.)
Preliminaries
Choosing a Cryptography Library
In the examples contained on this page, I will be using the Sodium cryptography library. Specifically, my example code will be written with the Sodium-Plus library for JavaScript, since it strikes a good balance between performance and being cross-platform.const { SodiumPlus } = require('sodium-plus');(async function() { // Select a backend automatically const sodium = await SodiumPlus.auto(); // Do other stuff here})();
Libsodium is generally the correct choice for developing cryptography features in software, and is available in most programming languages,
If you’re prone to choose a different library, you should consult your cryptographer (and yes, you should have one on your payroll if you’re doing things different) about your design choices.
Threat Modelling
Remember above when I said, “You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing”?How far you go in implementing the steps outlined on this blog post should be informed by a threat model, not an ad hoc judgment.
For example, if you’re encrypting user data and storing it in the cloud, you probably want to pass the Mud Puddle Test:
1. First, drop your device(s) in a mud puddle.
2. Next, slip in said puddle and crack yourself on the head. When you regain consciousness you’ll be perfectly fine, but won’t for the life of you be able to recall your device passwords or keys.
3. Now try to get your cloud data back.Did you succeed? If so, you’re screwed. Or to be a bit less dramatic, I should say: your cloud provider has access to your ‘encrypted’ data, as does the government if they want it, as does any rogue employee who knows their way around your provider’s internal policy checks.
Matthew Green describes the Mud Puddle Test, which Apple products definitely don’t pass.
If you must fail the Mud Puddle Test for your users, make sure you’re clear and transparent about this in the documentation for your product or service.
(Art by Swizz.)
I. Symmetric-Key Encryption
The easiest piece of this puzzle is to encrypt data in transit between both ends (thus, satisfying the loosest definition of end-to-end encryption).At this layer, you already have some kind of symmetric key to use for encrypting data before you send it, and for decrypting it as you receive it.
For example, the following code will encrypt/decrypt strings and return hexadecimal strings with a version prefix.
const VERSION = "v1";/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, key, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(50)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, key, aad ); return plaintext.toString('utf-8');}
Under-the-hood, this is using XChaCha20-Poly1305, which is less sensitive to timing leaks than AES-GCM. However, like AES-GCM, this encryption mode doesn’t provide message- or key-commitment.
If you want key commitment, you should derive two keys from
$keyusing a KDF based on hash functions: One for actual encryption, and the other as a key commitment value.If you want message commitment, you can use AES-CTR + HMAC-SHA256 or XChaCha20 + BLAKE2b-MAC.
If you want both, ask Taylor Campbell about his BLAKE3-based design.
A modified version of the above code with key-commitment might look like this:
const VERSION = "v2";/** * Derive an encryption key and a commitment hash. * @param {CryptographyKey} key * @param {Uint8Array} nonce * @returns {{encKey: CryptographyKey, commitment: Uint8Array}} */async function deriveKeys(key, nonce) { const encKey = new CryptographyKey(await sodium.crypto_generichash( new Uint8Array([0x01].append(nonce)), key )); const commitment = await sodium.crypto_generichash( new Uint8Array([0x02].append(nonce)), key ); return {encKey, commitment};}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const {encKey, commitment} = await deriveKeys(key, nonce); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, encKey, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(commitment) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(114)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const storedCommitment = await sodium.sodium_hex2bin(encrypted.slice(50, 114)); const {encKey, commitment} = await deriveKeys(key, nonce); if (!(await sodium.sodium_memcmp(storedCommitment, commitment))) { throw new Error("Incorrect commitment value"); } const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, encKey, aad ); return plaintext.toString('utf-8');}
Another design choice you might make is to encode ciphertext with base64 instead of hexadecimal. That doesn’t significantly alter the design here, but it does mean your decoding logic has to accommodate this.
You SHOULD version your ciphertexts, and include this in the AAD provided to your AEAD encryption mode. I used “v1” and “v2” as a version string above, but you can use your software name for that too.
II. Key Agreement
If you’re not familiar with Elliptic Curve Diffie-Hellman or Authenticated Key Exhcanges, the two of the earliest posts on this blog were dedicated to those topics.Key agreement in libsodium uses Elliptic Curve Diffie-Hellman over Curve25519, or X25519 for short.
There are many schools of thought for extending ECDH into an authenticated key exchange protocol.
We’re going to implement what the Signal Protocol calls X3DH instead of doing some interactive EdDSA + ECDH hybrid, because X3DH provides cryptographic deniability (see this section of the X3DH specification for more information).
For the moment, I’m going to assume a client-server model. That may or may not be appropriate for your design. You can substitute “the server” for “the other participant” in a peer-to-peer configuration.
Head’s up: This section of the blog post is code-heavy.
Update (November 23, 2020): I implemented this design in TypeScript, if you’d like something tangible to work with. I call my library, Rawr X3DH.
X3DH Pre-Key Bundles
Each participant will need to upload an Ed25519 identity key once (which is a detail covered in another section), which will be used to sign bundles of X25519 public keys to use for X3DH.Your implementation will involve a fair bit of boilerplate, like so:
/** * Generate an X25519 keypair. * * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}} */async function generateKeyPair() { const keypair = await sodium.crypto_box_keypair(); return { secretKey: await sodium.crypto_box_secretkey(keypair), publicKey: await sodium.crypto_box_publickey(keypair) };}/** * Generates some number of X25519 keypairs. * * @param {number} preKeyCount * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}[]} */async function generateBundle(preKeyCount = 100) { const bundle = []; for (let i = 0; i < preKeyCount; i++) { bundle.push(await generateKeyPair()); } return bundle;}/** * BLAKE2b( len(PK) | PK_0, PK_1, ... PK_n ) * * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function prehashPublicKeysForSigning(publicKeys) { const hashState = await sodium.crypto_generichash_init(); // First, update the state with the number of public keys const pkLen = new Uint8Array([ (publicKeys.length >>> 24) & 0xff, (publicKeys.length >>> 16) & 0xff, (publicKeys.length >>> 8) & 0xff, publicKeys.length & 0xff ]); await sodium.crypto_generichash_update(hashState, pkLen); // Next, update the state with each public key for (let pk of publicKeys) { await sodium.crypto_generichash_update( hashState, pk.getBuffer() ); } // Return the finalized BLAKE2b hash return await sodium.crypto_generichash_final(hashState);}/** * Signs a bundle. Returns the signature. * * @param {Ed25519SecretKey} signingKey * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function signBundle(signingKey, publicKeys) { return sodium.crypto_sign_detached( await prehashPublicKeysForSigning(publicKeys), signingKey );}/** * This is just so you can see how verification looks. * * @param {Ed25519PublicKey} verificationKey * @param {X25519PublicKey[]} publicKeys * @param {Uint8Array} signature */async function verifyBundle(verificationKey, publicKeys, signature) { return sodium.crypto_sign_verify_detached( await prehashPublicKeysForSigning(publicKeys), verificationKey, signature );}
This boilerplate exists just so you can do something like this:
/** * Generate some number of X25519 keypairs. * Persist the bundle. * Sign the bundle of publickeys with the Ed25519 secret key. * Return the signed bundle (which can be transmitted to the server.) * * @param {Ed25519SecretKey} signingKey * @param {number} numKeys * @returns {{signature: string, bundle: string[]}} */async function x3dh_pre_key(signingKey, numKeys = 100) { const bundle = await generateBundle(numKeys); const publicKeys = bundle.map(x => x.publicKey); const signature = await signBundle(signingKey, publicKeys); // This is a stub; how you persist it is app-specific: persistBundleNotDefinedHere(signingKey, bundle); // Hex-encode all the public keys const encodedBundle = []; for (let pk of publicKeys) { encodedBundle.push(await sodium.sodium_bin2hex(pk.getBuffer())); } return { 'signature': await sodium.sodium_bin2hex(signature), 'bundle': encodedBundle };}
And then you can drop the output of
x3dh_pre_key(secretKey)into a JSON-encoded HTTP request.In accordance to Signal’s X3DH spec, you want to use
x3dh_pre_key(secretKey, 1)to generate the “signed pre-key” bundle andx3dn_pre_key(secretKey, 100)when pushing 100 one-time keys to the server.X3DH Initiation
This section conforms to the Sending the Initial Message section of the X3DH specification.When you initiate a conversation, the server should provide you with a bundle containing:
- Your peer’s Identity key (an Ed25519 public key)
- Your peer’s current Signed Pre-Key (an X25519 public key)
- (If any remain unburned) One of your key’s One-Time Keys (an X25519 public key) — and then delete it
If we assume the structure of this response looks like this:
{ "IdentityKey": "...", "SignedPreKey": { "Signature": "..." "PreKey": "..." }, "OneTimeKey": "..." // or NULL}
Then we can write the initiation step of the handshake like so:
/** * Get SK for initializing an X3DH handshake * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} senderKey */async function x3dh_initiate_send_get_sk(r, senderKey) { const identityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey) ); const signedPreKey = new X25519PublicKey( await sodium.sodium_hex2bin(r.SignedPreKey.PreKey) ); const signature = await sodium.sodium_hex2bin(r.SignedPreKey.Signature); // Check signature const valid = await verifyBundle(identityKey, [signedPreKey], signature); if (!valid) { throw new Error("Invalid signature"); } const ephemeral = await generateKeyPair(); const ephSecret = ephemeral.secretKey; const ephPublic = ephemeral.publicKey; // Turn the Ed25519 keys into X25519 keys for X3DH: const senderX = await sodium.crypto_sign_ed25519_sk_to_curve25519(senderKey); const recipientX = await sodium.crypto_sign_ed25519_pk_to_curve25519(identityKey); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(senderX, signedPreKey); const DH2 = await sodium.crypto_scalarmult(ephSecret, recipientX); const DH3 = await sodium.crypto_scalarmult(ephSecret, signedPreKey); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( ephSecret, new X25519PublicKey(await sodium.sodium_hex2bin(r.OneTimeKey)) ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); ephSecret.wipe(); senderX.wipe(); return { IK: identityKey, EK: ephPublic, SK: SK, OTK: r.OneTimeKey // might be NULL };}/** * Initialize an X3DH handshake * * @param {string} recipientIdentity - Some identifier for the user * @param {Ed25519SecretKey} secretKey - Sender's secret key * @param {Ed25519PublicKey} publicKey - Sender's public key * @param {string} message - The initial message to send * @returns {object} */async function x3dh_initiate_send(recipientIdentity, secretKey, publicKey, message) { const r = await get_server_response(recipientIdentity); const {IK, EK, SK, OTK} = await x3dh_initiate_send_get_sk(r, secretKey); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(publicKey.getBuffer()) .concat(IK.getBuffer()) ) ); /* * We're going to set the session key for our recipient to SK. * This might invoke a ratchet. * * Either SK or the output of the ratchet derived from SK * will be returned by getEncryptionKey(). */ await setSessionKey(recipientIdentity, SK); const encrypted = await encryptData( message, await getEncryptionKey(recipientIdentity), assocData ); return { "Sender": my_identity_string, "IdentityKey": await sodium.sodium_bin2hex(publicKey), "EphemeralKey": await sodium.sodium_bin2hex(EK), "OneTimeKey": OTK, "CipherText": encrypted };}
We didn’t define
setSessionKey()orgetEncryptionKey()above. It will be covered later.X3DH – Receiving an Initial Message
This section implements the Receiving the Initial Message section of the X3DH Specification.We’re going to assume the structure of the request looks like this:
{ "Sender": "...", "IdentityKey": "...", "EphemeralKey": "...", "OneTimeKey": "...", "CipherText": "..."}
The code to handle this should look like this:
/** * Handle an X3DH initiation message as a receiver * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} identitySecret * @param {Ed25519PublicKey} identityPublic * @param {Ed25519SecretKey} preKeySecret */async function x3dh_initiate_recv_get_sk( r, identitySecret, identityPublic, preKeySecret) { // Decode strings const senderIdentityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey), ); const ephemeral = new X25519PublicKey( await sodium.sodium_hex2bin(r.EphemeralKey), ); // Ed25519 -> X25519 const senderX = await sodium.crypto_sign_ed25519_pk_to_curve25519(senderIdentityKey); const recipientX = await sodium.crypto_sign_ed25519_sk_to_curve25519(identitySecret); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(preKeySecret, senderX); const DH2 = await sodium.crypto_scalarmult(recipientX, ephemeral); const DH3 = await sodium.crypto_scalarmult(preKeySecret, ephemeral); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( await fetchAndWipeOneTimeSecretKey(r.OneTimeKey), ephemeral ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); recipientX.wipe(); return { Sender: r.Sender, SK: SK, IK: senderIdentityKey };}/** * Initiate an X3DH handshake as a recipient * * @param {object} req - Request object * @returns {string} - The initial message */async function x3dh_initiate_recv(req) { const {identitySecret, identityPublic} = await getIdentityKeypair(); const {preKeySecret, preKeyPublic} = await getPreKeyPair(); const {Sender, SK, IK} = await x3dh_initiate_recv_get_sk( req, identitySecret, identityPublic, preKeySecret, preKeyPublic ); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(IK.getBuffer()) .concat(identityPublic.getBuffer()) ) ); try { await setSessionKey(senderIdentity, SK); return decryptData( req.CipherText, await getEncryptionKey(senderIdentity), assocData ); } catch (e) { await destroySessionKey(senderIdentity); throw e; }}
And with that, you’ve successfully implemented X3DH and symmetric encryption in JavaScript.
We abstracted some of the details away (i.e.
kdf(), the transport mechanisms, the session key management mechanisms, and a few others). Some of them will be highly specific to your application, so it doesn’t make a ton of sense to flesh them out.One thing to keep in mind: According to the X3DH specification, participants should regularly (e.g. weekly) replace their Signed Pre-Key in the server with a fresh one. They should also publish more One-Time Keys when they start to run low.
If you’d like to see a complete reference implementation of X3DH, as I mentioned before, Rawr-X3DH implements it in TypeScript.
Session Key Management
Using X3DH to for every message is inefficient and unnecessary. Even the Signal Protocol doesn’t do that.Instead, Signal specifies a Double Ratchet protocol that combines a Symmetric-Key Ratchet on subsequent messages, and a Diffie-Hellman-based ratcheting protocol.
Signal even specifies integration guidelines for the Double Ratchet with X3DH.
It’s worth reading through the specification to understand their usages of Key-Derivation Functions (KDFs) and KDF Chains.
Although it is recommended to use HKDF as the Signal protocol specifies, you can strictly speaking use any secure keyed PRF to accomplish the same goal.
What follows is an example of a symmetric KDF chain that uses BLAKE2b with 512-bit digests of the current session key; the leftmost half of the BLAKE2b digest becomes the new session key, while the rightmost half becomes the encryption key.
const SESSION_KEYS = {};/** * Note: In reality you'll want to have two separate sessions: * One for receiving data, one for sending data. * * @param {string} identity * @param {CryptographyKey} key */async function setSessionKey(identity, key) { SESSION_KEYS[identity] = key;}async function getEncryptionKey(identity) { if (!SESSION_KEYS[identity]) { throw new Error("No session key for " + identity"); } const blake2bMac = await sodium.crypto_generichash( SESSION_KEYS[identity], null, 64 ); SESSION_KEYS[identity] = new CryptographyKey(blake2bMac.slice(0, 32)); return new CryptographyKey(blake2bMac.slice(32, 64));}
In the interest of time, a full DHRatchet implementation is left as an exercise to the reader (since it’s mostly a state machine), but using the appropriate functions provided by sodium-plus (
crypto_box_keypair(),crypto_scalarmult()) should be relatively straightforward.Make sure your KDFs use domain separation, as per the Signal Protocol specifications.
Group Key Agreement
The Signal Protocol specified X3DH and the Double Ratchet for securely encrypting information between two parties.Group conversations are trickier, because you have to be able to encrypt information that multiple recipients can decrypt, add/remove participants to the conversation, etc.
(The same complexity comes with multi-device support for end-to-end encryption.)
The best design I’ve read to date for tackling group key agreement is the IETF Messaging Layer Security RFC draft.
I am not going to implement the entire MLS RFC in this blog post. If you want to support multiple devices or group conversations, you’ll want a complete MLS implementation to work with.
Brief Recap
That was a lot of ground to cover, but we’re not done yet.
(Art by Khia.)
So far we’ve tackled encryption, initial key agreement, and session key management. However, we did not flesh out how Identity Keys (which are signing keys–Ed25519 specifically–rather than Diffie-Hellman keys) are managed. That detail was just sorta hand-waved until now.
So let’s talk about that.
III. Identity Key Management
There’s a meme among technology bloggers to write a post titled “Falsehoods Programmers Believe About _____”.Fortunately for us, Identity is one of the topics that furries are positioned to understand better than most (due to fursonas): Identities have a many-to-many relationship with Humans.
In an end-to-end encryption protocol, each identity will consist of some identifier (phone number, email address, username and server hostname, etc.) and an Ed25519 keypair (for which the public key will be published).
But how do you know whether or not a given public key is correct for a given identity?
This is where we segue into one of the hard problems in cryptography, where the solutions available are entirely dependent on your threat model: Public Key Infrastructure (PKI).
Some common PKI designs include:
- Certificate Authorities (CAs) — TLS does this
- Web-of-Trust (WoT) — The PGP ecosystem does this
- Trust On First Use (TOFU) — SSH does this
- Key Transparency / Certificate Transparency (CT) — TLS also does this for ensuring CA-issued certificates are auditable (although it was originally meant to replace Certificate Authorities)
And you can sort of choose-your-own-adventure on this one, depending on what’s most appropriate for the type of software you’re building and who your customers are.
One design I’m particularly fond of is called Gossamer, which is a PKI design without Certificate Authorities, originally designed for making WordPress’s automatic updates more secure (i.e. so every developer can sign their theme and plugin updates).
Since we only need to maintain an up-to-date repository of Ed25519 identity keys for each participant in our end-to-end encryption protocol, this makes Gossamer a suitable starting point.
Gossamer specifies a limited grammar of Actions that can be performed: AppendKey, RevokeKey, AppendUpdate, RevokeUpdate, and AttestUpdate. These actions are signed and published to an append-only cryptographic ledger.
I would propose a sixth action: AttestKey, so you can have WoT-like assurances and key-signing parties. (If nothing else, you should be able to attest that the identity keys of other cryptographic ledgers in the network are authentic at a point in time.)
IV. Backdoor Resistance
In the previous section, I proposed the use of Gossamer as a PKI for Identity Keys. This would provide Ed25519 keypairs for use with X3DH and the Double Ratchet, which would in turn provide session keys to use for symmetric authenticated encryption.If you’ve implemented everything preceding this section, you have a full-stack end-to-end encryption protocol. But let’s make intelligence agencies and surveillance capitalists even more mad by making it impractical to backdoor our software (and impossible to silently backdoor it).
How do we pull that off?
You want Binary Transparency.
For us, the implementation is simple: Use Gossamer as it was originally intended (i.e. to secure your software distribution channels).
Gossamer provides up-to-date verification keys and a commitment to a cryptographic ledger of every software update. You can learn more about its inspiration here.
It isn’t enough to merely use Gossamer to manage keys and update signatures. You need independent third parties to use the AttestUpdate action to assert one or more of the following:
- That builds are reproducible from the source code.
- That they have reviewed the source code and found no evidence of backdoors or exploitable vulnerabilities.
(And then you should let your users decide which of these independent third parties they trust to vet software updates.)
Closing Remarks
The U.S. Government cries and moans a lot about “criminals going dark” and wonders a lot about how to solve the “going dark problem”.If more software developers implement end-to-end encryption in their communications software, then maybe one day they won’t be able to use dragnet surveillance to spy on citizens and they’ll be forced to do actual detective work to solve actual crimes.
Y’know, like their job description actually entails?
Let’s normalize end-to-end encryption. Let’s normalize backdoor-resistant software distribution.
Let’s collectively tell the intelligence community in every sophisticated nation state the one word they don’t hear often enough:
Especially if you’re a furry. Because we improve everything! :3
Questions You Might Have
What About Private Contact Discovery?
That’s one of the major reasons why the thing we’re building isn’t meant to compete with Signal (and it MUST NOT be advertised as such):Signal is a privacy tool, and their servers have no way of identifying who can contact who.
What we’ve built here isn’t a complete privacy solution, it’s only providing end-to-end encryption (and possibly making NSA employees cry at their desk).
Does This Design Work with Federation?
Yes. Each identifier string can be [username] at [hostname].What About Network Metadata?
If you want anonymity, you want to use Tor.Why Are You Using Ed25519 Keys for X3DH?
If you only read the key agreement section of this blog post and the fact that I’m passing around Ed25519 public keys seems weird, you might have missed the identity section of this blog post where I suggested piggybacking on another protocol called Gossamer to handle the distribution of Ed25519 public keys. (Gossamer is also beneficial for backdoor resistance in software update distribution, as described in the subsequent section.)Furthermore, we’re actually using birationally equivalent X25519 keys derived from the Ed25519 keypair for the X3DH step. This is a deviation from what Signal does (using X25519 keys everywhere, then inventing an EdDSA variant to support their usage).
const publicKeyX = await sodium.crypto_sign_ed25519_pk_to_curve25519(foxPublicKey);const secretKeyX = await sodium.crypto_sign_ed25519_sk_to_curve25519(wolfSecretKey);
(Using fox/wolf instead of Alice/Bob, because it’s cuter.)
This design pattern has a few advantages:
- It makes Gossamer integration seamless, which means you can use Ed25519 for identities and still have a deniable X3DH handshake for 1:1 conversations while implementing the rest of the designs proposed.
- This approach to X3DH can be implemented entirely with libsodium functions, without forcing you to write your own cryptography implementations (i.e. for XEdDSA).
The only disadvantages I’m aware of are:
- It deviates from Signal’s core design in a subtle way that means you don’t get to claim the exact same advantages Signal does when it comes to peer review.
- Some cryptographers are distrustful of the use of birationally equivalent X25519 keys from Ed25519 keys (although there isn’t a vulnerability any of them have been able to point me to that doesn’t involve torsion groups–which libsodium’s implementation already avoids).
If these concerns are valid enough to decide against my implementation above, I invite you to talk with cryptographers about your concerns and then propose alternatives.
Has Any of This Been Implemented Already?
You can find implementations for the designs discussed on this blog post below:
- Rawr-X3DH implements X3DH in TypeScript (added 2020-11-23)
I will update this section of the blog post as implementations surface.
https://soatok.blog/2020/11/14/going-bark-a-furrys-guide-to-end-to-end-encryption/
#authenticatedEncryption #authenticatedKeyExchange #crypto #cryptography #encryption #endToEndEncryption #libsodium #OnlinePrivacy #privacy #SecurityGuidance #symmetricEncryption

A few years ago, when the IETF’s Crypto Forum Research Group was deeply entrenched in debates about elliptic curves for security (which eventually culminated in RFC 7748 and RFC 8032), an IT Consultant showed up on the mailing list with their homemade cipher, Crystalline.
Mike Hamburg politely informed the consultant that the CFRG isn’t the right forum for proposing new symmetric ciphers, or even new modes for symmetric ciphers, and invited them to email them off-list.
If you’re not familiar with the CFRG, let me just say, this was on the more patient and measured responses I’ve ever read.
Naturally, the author of Crystalline responded with this:
I’m somewhat disappointed in your reply, as I presumed that someone with a stated interest in ciphers would be eager to investigate anything new to pop up that didn’t have obvious holes in it. It almost sounds like you have had your soul crushed by bureaucracy over the years and have lost all passion for this field.Full quote available here. It doesn’t get much better.

The discussion continued until Tony Arcieri dropped one of the most brutal takedowns of a cryptographic design in CFRG history.
I think the biggest problem though is all of this has already been pointed out to you repeatedly in other forums and you completely refuse to acknowledge that your cipher fails to meet the absolute most minimum criteria for a secure cipher.Tony Arcieri, landing a cryptographic 360 no-scope on Crystalline.
In spite of this mic drop moment, the author of Crystalline continued to double down and insist that a symmetric cipher doesn’t need to be indistinguishable from randomness to be secure (which, to severely understate the affairs, is simply not true).
Normally, when a cipher fails at the indistinguishable test, it’s subtle. This is what Crystalline ciphertexts look like.

Modern ciphers produce something that will look like white noise, like an old TV without the cable plugged in. There should be no discernible pattern.
Crystalline’s author remained convinced that Crystalline’s “131072-bit keys” and claims of “information-theoretic security” were compelling enough to warrant consideration by the standards body that keeps the Internet running.
This was in 2015. In the year 2021, I can safely say that Crystalline adoption never really took off.
Against Crackpot Crypto
Instances of Crackpot Cryptography don’t always look like Crystalline. Sometimes the authors are more charismatic, or have more financial resources to bedazzle would-be suckers^investors. Other times, they’re less brazen and keep their designs far away from the watchful gaze of expert opinions–lest their mistakes be exposed for all to see.
Crackpot cryptography is considered dangerous–not because we want people to avoid encryption entirely, but because crackpot cryptography offers a false sense of security. This leads to users acting in ways they wouldn’t if they knew there was little-to-no security. Due to the strictly performative nature of these security measures, I also like to call them Security Theater (although that term is more broadly applicable in other contexts).
The Cryptology community has a few defense mechanisms in place to prevent the real-world adoption of crackpot cryptography. More specifically, we have pithy mottos that distill best practices in a way that usually gets the intent across. (Hey, it’s something!) Unfortunately, the rest of the security industry outside of cryptology often weaponizes these mottos to promote useless and harmful gatekeeping.
The best example of this is the, “Don’t roll your own crypto!” motto.
They See Me Rollin’ [My Own Crypto]
Crackpots never adhere to this rule, so anyone who violates it immediately or often, with wild abandon, can be safely dismissed for kooky behavior.
But if taken to its literal, logical extreme, this rule mandates that nobody would ever write cryptographic code and we wouldn’t have cryptography libraries to begin with. So, clearly, it’s a rule meant to be sometimes broken.
This is why some cryptography engineers soften the message a bit and encourage tinkering for the sake of education. The world needs more software engineers qualified to write cryptography.
After all, you wouldn’t expect to hear “Don’t roll your own crypto” being levied against Jason Donenfeld (WireGuard) or Frank Denis (libsodium), despite the fact that both of those people did just that.
But what about a high-level library that defers to libsodium for its actual crypto implementations?
In a twist that surprises no one, lazy heuristics have a high false positive rate. In this case, the lazy heuristic is both, “What qualifies as rolling one’s own crypto?” as well as, “When is it safe to break this rule?”
More broadly, though, is that these knee-jerk responses are a misfiring defense mechanism intended to stop quacks from taking all the air out of the room.
It doesn’t always work, though. There have been a few downright absurd instances of crackpot cryptography in the past few years.
Modern Examples of Crypto Crackpottery
Craig Wright’s Sartre Signature Scam
Satoshi Nakamoto is the alias of the anonymous cryptographer that invented Bitcoin. In the years since Satoshi has gone quiet, a few cranks have come out of the woodwork to claim to be the real Satoshi.
Craig Wright is one of the more famous Satoshi impersonators due to his Sartre Signature Scam.
Satoshi’s earliest Bitcoin transactions are public. If you can lift the public key and signature from the transaction and then replay them in a different context as “proof” that you’re Satoshi, you can produce a proof of identity that validates without having to possess Satoshi’s private key. Then you can just wildly claim it’s a signature that validates the text of some philosopher’s prose and a lot of people will believe you.
With a little bit of showmanship added on, you too can convince Gavin Anderson by employing this tactic. (Or maybe not; I imagine he’s learned his lesson by now.)
Time AI
Crown Sterling’s sponsored talk at Black Hat USA 2019 is the most vivid example of crackpot cryptography in most people’s minds.
Even the name “Time AI” just screams buzzword soup, so it should come as no surprise that their talk covered a lot of nonsense: “quasi-prime numbers”, “infinite wave conjugations”, “nano-scale of time”, “speed of AI oscillations”, “unified physics cosmology”, and “multi-dimensional encryption technology”.
Naturally, this pissed a lot of cryptographers off, and the normally even-keeled Dan Guido of Trail of Bits actually called them out on their bullshit during their presentation’s Q&A section.
https://twitter.com/dguido/status/1159579063540805632?lang=en
For most people, the story ended with a bunch of facepalms. But Crown Sterling doubled down and published a press release claiming the ability to break 256-bit RSA keys.
Amusingly, their attack took 50 seconds–which is a lot slower than the standard RSA factoring attacks for small key sizes.
(For those who are missing context: In order to be secure, RSA requires public key sizes in excess of 2048 bits. Breaking 256-bit RSA should take less than a minute on any modern PC.)
Terra Quantum
Earlier this week, Bloomberg news ran a story titled, A Swiss Company Says It Found Weakness That Imperils Encryption. If you only read the first few paragraphs, it’s really clear that the story basically boils down to, “Swiss Company realizes there’s an entire discipline of computer science dedicated to quantum computers and the risks they pose to cryptography.”
Here’s a quick primer on quantum computers and cryptography:
If a practical quantum computer is ever built, it can immediately break all of the asymmetric cryptography used on the Internet today: RSA, DSA, Diffie-Hellman, Elliptic Curve Cryptography, etc. The attack costs to break these algorithms vary, but are generally in the 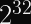
The jury is still out on whether or not quantum computers will ever be practical. Just in case, a lot of cryptographers are working on post-quantum cryptography (algorithms that are secure even against quantum computers).
Symmetric cryptography fares a lot better: The attack costs are roughly reduced by a factor of 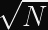
So it’s a little strange that they open with:
The company said that its research found vulnerabilities that affect symmetric encryption ciphers, including the Advanced Encryption Standard, or AES, which is widely used to secure data transmitted over the internet and to encrypt files. Using a method known as quantum annealing, the company said its research found that even the strongest versions of AES encryption may be decipherable by quantum computers that could be available in a few years from now.From the Bloomberg article.
Uh, no.
Let’s do some math: 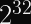
You can break 128-bit ciphers in 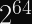
What does 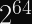
https://www.youtube.com/watch?v=vWXP3DvH8OQ
In 2012, we could break DES (which has 56-bit keys) in 24 hours with FPGAs dedicated to the task. Since each extra bit of security doubles the search space, we can extrapolate that 64-bits would require 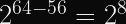
So even with a quantum computer in hand, you would need to spend several months trying to break a single 128-bit AES key.

If this were just one poorly written Bloomberg article put together by someone who vastly misunderstands post-quantum cryptography, Terra Quantum AG wouldn’t require much mention.
But, as with other crackpots before them, Terra Quantum doubled down with yet another press release published on Business Wire. (Archived.)
Terra Quantum realised that the AES is fairly secure against already identified algorithms but may appear fenceless against upcoming threats. To build the defence, Terra Quantum set out to look for a weakness by testing the AES against new algorithms. They Terra Quantum discovered a weakness on the message-digest algorithm MD5.
Okay, so in the time that elapsed between the two press releases, they realized they couldn’t realistically break AES with a quantum computer, but…
MD5? MD-fucking-FIVE?! This is a joke right?

(Art by Khia.)
The press release goes on to almost have a moment of self-awareness, but ultimately fails to do so:
The Terra Quantum team found that one can crack an algorithm using a quantum annealer containing about 20,000 qubits. No such annealer exists today, and while it is impossible to predict when it may be created, it is conceivable that such an annealer could become available to hackers in the future.(Emphasis mine.)
Yikes. There’s a lot of bullshit in that sentence, but it only gets zanier from there.
https://twitter.com/boazbaraktcs/status/1359283973789278208
Here’s an actual quote from Terra Quantum’s CTOs, Gordey Lesovik and Valerii Vinokur about the “solution” to their imaginary problem:
“A new protocol derives from the notion that Quantum Demon is a small beast. The standard approach utilises the concept that the Demon hired by an eavesdropper (Eva) is a King Kong-like hundred kilometres big monster who can successfully use all the transmission line losses to decipher the communication. But since real Quantum Demons are small, Eva has to recruit an army of a billion to successfully collect all the scattered waves leaking from the optical fibre that she needs for efficient deciphering. Terra Quantum proposes an innovative technique utilizing the fact that such an army cannot exist – in accord with the second law of thermodynamics.”I seriously cannot fucking make this shit up. My fiction writing skills are simply not good enough.
I don’t partake in recreational drugs, but if I did, I’d probably want whatever they’re on.
It’s important to note, at no point does Terra Quantum show their work. No source code or technical papers are published; just a lot of press releases that make exaggerated claims about quantum computers and totally misunderstands post-quantum cryptography.
Takeaways
If you see a press release on Business Wire about cryptography, it’s probably a scam. Real cryptographers publish on ePrint and then peer-reviewed journals, present their talks at conferences (but not sponsored talks), and exercise radical transparency with all facets of their work.
Publish the source code, Luke!
Cryptography has little patience for swindlers, liars, and egomaniacs. (Although cryptocurrency seems more amenable to those personalities.) That doesn’t stop them from trying, of course.
If you’re reading this blog post and feel like learning about cryptography and cryptanalysis and feel put off by the “don’t roll your own crypto” mantra, and its implied gatekeeping, I hope it’s clear by now who that phrase was mostly intended for and why.
https://soatok.blog/2021/02/09/crackpot-cryptography-and-security-theater/
#asymmetricCryptography #crackpots #CrownSterling #cryptography #kooks #postQuantumCryptography #quantumComputers #scamArtists #scammers #scams #symmetricCryptography #TerraQuantum #TimeAI
A few years ago, when the IETF’s Crypto Forum Research Group was deeply entrenched in debates about elliptic curves for security (which eventually culminated in RFC 7748 and RFC 8032), an IT Consultant showed up on the mailing list with their homemade cipher, Crystalline.Mike Hamburg politely informed the consultant that the CFRG isn’t the right forum for proposing new symmetric ciphers, or even new modes for symmetric ciphers, and invited them to email them off-list.
If you’re not familiar with the CFRG, let me just say, this was on the more patient and measured responses I’ve ever read.
Naturally, the author of Crystalline responded with this:
I’m somewhat disappointed in your reply, as I presumed that someone with a stated interest in ciphers would be eager to investigate anything new to pop up that didn’t have obvious holes in it. It almost sounds like you have had your soul crushed by bureaucracy over the years and have lost all passion for this field.Full quote available here. It doesn’t get much better.
Really dude? (Art by Khia.)
The discussion continued until Tony Arcieri dropped one of the most brutal takedowns of a cryptographic design in CFRG history.
I think the biggest problem though is all of this has already been pointed out to you repeatedly in other forums and you completely refuse to acknowledge that your cipher fails to meet the absolute most minimum criteria for a secure cipher.Tony Arcieri, landing a cryptographic 360 no-scope on Crystalline.
In spite of this mic drop moment, the author of Crystalline continued to double down and insist that a symmetric cipher doesn’t need to be indistinguishable from randomness to be secure (which, to severely understate the affairs, is simply not true).Normally, when a cipher fails at the indistinguishable test, it’s subtle. This is what Crystalline ciphertexts look like.
Data encrypted with Crystalline, provided in the CFRG mailing list.
Modern ciphers produce something that will look like white noise, like an old TV without the cable plugged in. There should be no discernible pattern.
Crystalline’s author remained convinced that Crystalline’s “131072-bit keys” and claims of “information-theoretic security” were compelling enough to warrant consideration by the standards body that keeps the Internet running.
This was in 2015. In the year 2021, I can safely say that Crystalline adoption never really took off.
Against Crackpot Crypto
Instances of Crackpot Cryptography don’t always look like Crystalline. Sometimes the authors are more charismatic, or have more financial resources to bedazzle would-besuckers^investors. Other times, they’re less brazen and keep their designs far away from the watchful gaze of expert opinions–lest their mistakes be exposed for all to see.Crackpot cryptography is considered dangerous–not because we want people to avoid encryption entirely, but because crackpot cryptography offers a false sense of security. This leads to users acting in ways they wouldn’t if they knew there was little-to-no security. Due to the strictly performative nature of these security measures, I also like to call them Security Theater (although that term is more broadly applicable in other contexts).
The Cryptology community has a few defense mechanisms in place to prevent the real-world adoption of crackpot cryptography. More specifically, we have pithy mottos that distill best practices in a way that usually gets the intent across. (Hey, it’s something!) Unfortunately, the rest of the security industry outside of cryptology often weaponizes these mottos to promote useless and harmful gatekeeping.
The best example of this is the, “Don’t roll your own crypto!” motto.
They See Me Rollin’ [My Own Crypto]
Crackpots never adhere to this rule, so anyone who violates it immediately or often, with wild abandon, can be safely dismissed for kooky behavior.But if taken to its literal, logical extreme, this rule mandates that nobody would ever write cryptographic code and we wouldn’t have cryptography libraries to begin with. So, clearly, it’s a rule meant to be sometimes broken.
This is why some cryptography engineers soften the message a bit and encourage tinkering for the sake of education. The world needs more software engineers qualified to write cryptography.
After all, you wouldn’t expect to hear “Don’t roll your own crypto” being levied against Jason Donenfeld (WireGuard) or Frank Denis (libsodium), despite the fact that both of those people did just that.
But what about a high-level library that defers to libsodium for its actual crypto implementations?
In a twist that surprises no one, lazy heuristics have a high false positive rate. In this case, the lazy heuristic is both, “What qualifies as rolling one’s own crypto?” as well as, “When is it safe to break this rule?”
More broadly, though, is that these knee-jerk responses are a misfiring defense mechanism intended to stop quacks from taking all the air out of the room.
It doesn’t always work, though. There have been a few downright absurd instances of crackpot cryptography in the past few years.
Modern Examples of Crypto Crackpottery
Craig Wright’s Sartre Signature Scam
Satoshi Nakamoto is the alias of the anonymous cryptographer that invented Bitcoin. In the years since Satoshi has gone quiet, a few cranks have come out of the woodwork to claim to be the real Satoshi.Craig Wright is one of the more famous Satoshi impersonators due to his Sartre Signature Scam.
Satoshi’s earliest Bitcoin transactions are public. If you can lift the public key and signature from the transaction and then replay them in a different context as “proof” that you’re Satoshi, you can produce a proof of identity that validates without having to possess Satoshi’s private key. Then you can just wildly claim it’s a signature that validates the text of some philosopher’s prose and a lot of people will believe you.
With a little bit of showmanship added on, you too can convince Gavin Anderson by employing this tactic. (Or maybe not; I imagine he’s learned his lesson by now.)
Time AI
Crown Sterling’s sponsored talk at Black Hat USA 2019 is the most vivid example of crackpot cryptography in most people’s minds.Even the name “Time AI” just screams buzzword soup, so it should come as no surprise that their talk covered a lot of nonsense: “quasi-prime numbers”, “infinite wave conjugations”, “nano-scale of time”, “speed of AI oscillations”, “unified physics cosmology”, and “multi-dimensional encryption technology”.
Naturally, this pissed a lot of cryptographers off, and the normally even-keeled Dan Guido of Trail of Bits actually called them out on their bullshit during their presentation’s Q&A section.
https://twitter.com/dguido/status/1159579063540805632?lang=en
For most people, the story ended with a bunch of facepalms. But Crown Sterling doubled down and published a press release claiming the ability to break 256-bit RSA keys.
Amusingly, their attack took 50 seconds–which is a lot slower than the standard RSA factoring attacks for small key sizes.
(For those who are missing context: In order to be secure, RSA requires public key sizes in excess of 2048 bits. Breaking 256-bit RSA should take less than a minute on any modern PC.)
Terra Quantum
Earlier this week, Bloomberg news ran a story titled, A Swiss Company Says It Found Weakness That Imperils Encryption. If you only read the first few paragraphs, it’s really clear that the story basically boils down to, “Swiss Company realizes there’s an entire discipline of computer science dedicated to quantum computers and the risks they pose to cryptography.”Here’s a quick primer on quantum computers and cryptography:
If a practical quantum computer is ever built, it can immediately break all of the asymmetric cryptography used on the Internet today: RSA, DSA, Diffie-Hellman, Elliptic Curve Cryptography, etc. The attack costs to break these algorithms vary, but are generally in the
range (for numbers of queries).
The jury is still out on whether or not quantum computers will ever be practical. Just in case, a lot of cryptographers are working on post-quantum cryptography (algorithms that are secure even against quantum computers).
Symmetric cryptography fares a lot better: The attack costs are roughly reduced by a factor of
. This makes a 128-bit secure cipher have only a 64-bit security level, which is pretty terrible, but a 256-bit secure cipher remains at the 128-bit security level even with practical quantum computers.
So it’s a little strange that they open with:
The company said that its research found vulnerabilities that affect symmetric encryption ciphers, including the Advanced Encryption Standard, or AES, which is widely used to secure data transmitted over the internet and to encrypt files. Using a method known as quantum annealing, the company said its research found that even the strongest versions of AES encryption may be decipherable by quantum computers that could be available in a few years from now.From the Bloomberg article.
Uh, no.Let’s do some math:
calculations can be performed in seconds on modern computers. If we assume that practical quantum computers are also as fast as classical computers, it’s safe to assume this will hold true as well.
You can break 128-bit ciphers in
time, using Grover’s algorithm. You can’t break 256-bit ciphers in any practical time, even with the quantum computer speed-up. Most software prefers 256-bit AES over 128-bit AES for this reason.
What does
time look like?
https://www.youtube.com/watch?v=vWXP3DvH8OQ
In 2012, we could break DES (which has 56-bit keys) in 24 hours with FPGAs dedicated to the task. Since each extra bit of security doubles the search space, we can extrapolate that 64-bits would require
or 256 days.
So even with a quantum computer in hand, you would need to spend several months trying to break a single 128-bit AES key.
(Art by Scruff Kerfluff.)
If this were just one poorly written Bloomberg article put together by someone who vastly misunderstands post-quantum cryptography, Terra Quantum AG wouldn’t require much mention.
But, as with other crackpots before them, Terra Quantum doubled down with yet another press release published on Business Wire. (Archived.)
Terra Quantum realised that the AES is fairly secure against already identified algorithms but may appear fenceless against upcoming threats. To build the defence, Terra Quantum set out to look for a weakness by testing the AES against new algorithms. They Terra Quantum discovered a weakness on the message-digest algorithm MD5.
Okay, so in the time that elapsed between the two press releases, they realized they couldn’t realistically break AES with a quantum computer, but…MD5? MD-fucking-FIVE?! This is a joke right?
“Let’s hype up a hypothetical attack leveraged by quantum computers and then direct it at the most widely broken hash function on Earth.” – Shorter Terra Quantum
(Art by Khia.)The press release goes on to almost have a moment of self-awareness, but ultimately fails to do so:
The Terra Quantum team found that one can crack an algorithm using a quantum annealer containing about 20,000 qubits. No such annealer exists today, and while it is impossible to predict when it may be created, it is conceivable that such an annealer could become available to hackers in the future.(Emphasis mine.)
Yikes. There’s a lot of bullshit in that sentence, but it only gets zanier from there.https://twitter.com/boazbaraktcs/status/1359283973789278208
Here’s an actual quote from Terra Quantum’s CTOs, Gordey Lesovik and Valerii Vinokur about the “solution” to their imaginary problem:
“A new protocol derives from the notion that Quantum Demon is a small beast. The standard approach utilises the concept that the Demon hired by an eavesdropper (Eva) is a King Kong-like hundred kilometres big monster who can successfully use all the transmission line losses to decipher the communication. But since real Quantum Demons are small, Eva has to recruit an army of a billion to successfully collect all the scattered waves leaking from the optical fibre that she needs for efficient deciphering. Terra Quantum proposes an innovative technique utilizing the fact that such an army cannot exist – in accord with the second law of thermodynamics.”I seriously cannot fucking make this shit up. My fiction writing skills are simply not good enough.
I don’t partake in recreational drugs, but if I did, I’d probably want whatever they’re on.It’s important to note, at no point does Terra Quantum show their work. No source code or technical papers are published; just a lot of press releases that make exaggerated claims about quantum computers and totally misunderstands post-quantum cryptography.
Takeaways
If you see a press release on Business Wire about cryptography, it’s probably a scam. Real cryptographers publish on ePrint and then peer-reviewed journals, present their talks at conferences (but not sponsored talks), and exercise radical transparency with all facets of their work.Publish the source code, Luke!
Cryptography has little patience for swindlers, liars, and egomaniacs. (Although cryptocurrency seems more amenable to those personalities.) That doesn’t stop them from trying, of course.
If you’re reading this blog post and feel like learning about cryptography and cryptanalysis and feel put off by the “don’t roll your own crypto” mantra, and its implied gatekeeping, I hope it’s clear by now who that phrase was mostly intended for and why.
https://soatok.blog/2021/02/09/crackpot-cryptography-and-security-theater/
#asymmetricCryptography #crackpots #CrownSterling #cryptography #kooks #postQuantumCryptography #quantumComputers #scamArtists #scammers #scams #symmetricCryptography #TerraQuantum #TimeAI

If you’re ever tasked with implementing a cryptography feature–whether a high-level protocol or a low-level primitive–you will have to take special care to ensure you’re not leaking secret information through side-channels.
The descriptions of algorithms you learn in a classroom or textbook are not sufficient for real-world use. (Yes, that means your toy RSA implementation based on GMP from your computer science 101 class isn’t production-ready. Don’t deploy it.)
But what are these elusive side-channels exactly, and how do you prevent them? And in cases where you cannot prevent them, how can you mitigate the risk to your users?

Contents
- Cryptographic Side-Channels
- Side-Channel Prevention and Mitigation
- Design Patterns for Algorithmic Constant-Time Code
- Constant-Time String Comparison
- Alternative: “Double HMAC” String Comparison
- Constant-Time Conditional Select
- Constant-Time String Inequality Comparison
- Constant-Time Integer Multiplication
- Constant-Time Integer Division
- Constant-Time Modular Inversion
- Constant-Time Null-Byte Trimming
- Further Reading and Online Resources
- Errata
Cryptographic Side-Channels
The concept of a side-channel isn’t inherently cryptographic, as Taylor Hornby demonstrates, but a side-channel can be a game over vulnerability in a system meant to maintain confidentiality (even if only for its cryptography keys).
Cryptographic side-channels allow an attacker to learn secret data from your cryptography system. To accomplish this, the attacker doesn’t necessarily study the system’s output (i.e. ciphertext); instead, they observe some other measurement, such as how much time or power was spent performing an operation, or what kind of electromagnetic radiation was emitted.
Important: While being resistant to side-channels is a prerequisite for implementations to be secure, it isn’t in and of itself sufficient for security. The underlying design of the primitives, constructions, and high-level protocols needs to be secure first, and that requires a clear and specific threat model for what you’re building.
Constant-time ECDSA doesn’t help you if you reuse k-values like it’s going out of style, but variable-time ECDSA still leaks your secret key to anyone who cares to probe your response times. Secure cryptography is very demanding.

Timing Leaks
Timing side-channels leak secrets through how much time it takes for an operation to complete.
There are many different flavors of timing leakage, including:
- Fast-failing comparison functions (memcmp() in C)
- Cache-timing vulnerabilities (e.g. software AES)
- Memory access patterns
- Conditional branches controlled by secrets
The bad news about timing leaks is that they’re almost always visible to an attacker over the network (including over the Internet (PDF)).
The good news is that most of them can be prevented or mitigated in software.

Power Usage
Different algorithms or processor operations may require different amounts of power.
For example, squaring a large number may take less power than multiplying two different large numbers. This observation has led to the development of power analysis attacks against RSA.
Power analysis is especially relevant for embedded systems and smart cards, which are easier to extract a meaningful signal from than your desktop computer.
Some information leakage through power usage can be prevented through careful engineering (for example: BearSSL, which uses Montgomery multiplication instead of square-and-multiply).
But that’s not always an option, so generally these risks are mitigated.

Electromagnetic Emissions
Your computer is a reliable source of electromagnetic emissions (such as radio waves). Some of these emissions may reveal information about your cryptographic secrets, especially to an attacker with physical proximity to your device.
The good news is that research into EM emission side-channels isn’t as mature as side-channels through timing leaks or power usage. The bad news is that mitigations for breakthroughs will generally require hardware (e.g. electromagnetic shielding).
![[Glitching] [Glitching]](https://fika.grin.hu/photo/link/10390)
Side-Channel Prevention and Mitigation
Now that we’ve established a rough sense of some of the types of side-channels that are possible, we can begin to identify what causes them and aspire to prevent the leaks from happening–and where we can’t, to mitigate the risk to a reasonable level.
Note: To be clear, I didn’t cover all of the types of side-channels.
Prevention vs. Mitigation
Preventing a side-channel means eliminating the conditions that allow the information leak to occur in the first place. For timing leaks, this means making all algorithms constant-time.
There are entire classes of side-channel leaks that aren’t possible or practical to mitigate in software. When you encounter one, the best you can hope to do is mitigate the risk.
Ideally, you want to make the attack more expensive to pull off than the reward an attacker will gain from it.
What is Constant-Time?
https://www.youtube.com/watch?v=ZD_H1ePLylA
When an implementation is said to be constant-time, what we mean is that the execution time of the code is not a function of its secret inputs.
Vulnerable AES uses table look-ups to implement the S-Box. Constant-time AES is either implemented in hardware, or is bitsliced.
Malicious Environments and Algorithmic Constant-Time
One of the greatest challenges with writing constant-time code is distinguishing between algorithmic constant-time and provably constant-time. The main difference between the two is that you cannot trust your compiler (especially a JIT compiler), which may attempt to optimize your code in a way that reintroduces the side-channel you aspired to remove.
A sufficiently advanced compiler optimization is indistinguishable from an adversary.John Regehr, possibly with apologies to Arthur C. Clarke
For compiled languages, this is a tractable but expensive problem to solve: You simply have to formally verify everything from the source code to the compiler to the silicon chips that the code will be deployed on, and then audit your supply chain to prevent malicious tampering from going undetected.
For interpreted languages (e.g. PHP and JavaScript), this formal verification strategy isn’t really an option, unless you want to formally verify the runtime that interprets scripts and prove that the operations remain constant-time on top of all the other layers of distrust.
Is this level of paranoia really worth the effort?

For that reason, we’re going to assume that algorithmic constant-time is adequate for the duration of this blog post.
If your threat model prevents you from accepting this assumption, feel free to put in the extra effort yourself and tell me how it goes. After all, as a furry who writes blog posts in my spare time for fun, I don’t exactly have the budget for massive research projects in formal verification.
Mitigation with Blinding Techniques
The best mitigation for some side-channels is called blinding: Obfuscating the inputs with some random data, then deobfuscating the outputs with the same random data, such that your keys are not revealed.
Two well-known examples include RSA decryption and Elliptic Curve Diffie-Hellman. I’ll focus on the latter, since it’s not as widely covered in the literature (although several cryptographers I’ve talked with were somehow knowledgeable about it; I suspect gatekeeping is involved).
Blinded ECDH Key Exchange
In typical ECDH implementations, you will convert a point on a Weierstrass curve 
The exact conversion formula is (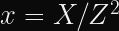
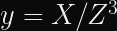
Where does 

It turns out, the choice for 
Choosing a random number means the calculations performed over Jacobian coordinates will be obscured by a randomly chosen factor 

I think it’s really cool how one small tweak to the runtime of an algorithm can make it significantly harder to attack.
Design Patterns for Algorithmic Constant-Time Code
Mitigation techniques are cool, but preventing side-channels is a better value-add for most software.
To that end, let’s look at some design patterns for constant-time software. Some of these are relatively common; others, not so much.

If you prefer TypeScript / JavaScirpt, check out Soatok’s constant-time-js library on Github / NPM.
Constant-Time String Comparison
Rather than using string comparison (== in most programming languages, memcmp() in C), you want to compare cryptographic secrets and/or calculated integrity checks with a secure compare algorithm, which looks like this:
- Initialize a variable (let’s call it D) to zero.
- For each byte of the two strings:
- Calculate (lefti XOR righti)
- Bitwise OR the current value of D with the result of the XOR, store the output in D
- When the loop has concluded, D will be equal to 0 if and only if the two strings are equal.
In code form, it looks like this:
<?phpfunction ct_compare(string $left, string $right): bool{ $d = 0; $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { return false; // Lengths differ } for ($i = 0; $i < $length; ++$i) { $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $d |= ($leftCharCode ^ $rightCharCode); } return $d === 0;}
In this example, I’m using PHP’s unpack() function to avoid cache-timing leaks with ord() and chr(). Of course, you can simply use hash_equals() instead of writing it yourself (PHP 5.6.0+).
Alternative: “Double HMAC” String Comparison
If the previous algorithm won’t work (i.e. because you’re concerned your JIT compiler will optimize it away), there is a popular alternative to consider. It’s called “Double HMAC” because it was traditionally used with Encrypt-Then-HMAC schemes.
The algorithm looks like this:
- Generate a random 256-bit key, K. (This can be cached between invocations, but it should be unpredictable.)
- Calculate HMAC-SHA256(K, left).
- Calculate HMAC-SHA256(K, right).
- Return true if the outputs of step 2 and 3 are equal.
This is provably secure, so long as HMAC-SHA256 is a secure pseudo-random function and the key K is unknown to the attacker.
In code form, the Double HMAC compare function looks like this:
<?phpfunction hmac_compare(string $left, string $right): bool{ static $k = null; if (!$k) $k = random_bytes(32); return ( hash_hmac('sha256', $left, $k) === hash_hmac('sha256', $right, $k) );}
Constant-Time Conditional Select
I like to imagine a conversation between a cryptography engineer and a Zen Buddhist, that unfolds like so:
- CE: “I want to eliminate branching side-channels from my code.”
- ZB: “Then do not have branches in your code.”
And that is precisely what we intend to do with a constant-time conditional select: Eliminate branches by conditionally returning between one of two strings, without an IF statement.

This isn’t as tricky as it sounds. We’re going to use XOR and two’s complement to achieve this.
The algorithm looks like this:
- Convert the selection bit (TRUE/FALSE) into a mask value (-1 for TRUE, 0 for FALSE). Bitwise, -1 looks like 111111111…1111111111, while 0 looks like 00000000…00000000.
- Copy the right string into a buffer, call it tmp.
- Calculate left XOR right, call it x.
- Return (tmp XOR (x AND mask)).
Once again, in code this algorithm looks like this:
<?phpfunction ct_select( bool $returnLeft, string $left, string $right): string { $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } // Mask byte $mask = (-$returnLeft) & 0xff; // X $x = (string) ($left ^ $right); // Output = Right XOR (X AND Mask) $output = ''; for ($i = 0; $i < $length; $i++) { $rightCharCode = unpack('C', $right[$i])[1]; $xCharCode = unpack('C', $x[$i])[1]; $output .= pack( 'C', $rightCharCode ^ ($xCharCode & $mask) ); } return $output;}
You can test this code for yourself here. The function was designed to read intuitively like a ternary operator.
A Word of Caution on Cleverness
In some languages, it may seem tempting to use the bitwise trickery to swap out pointers instead of returning a new buffer. But do not fall for this Siren song.
If, instead of returning a new buffer, you just swap pointers, what you’ll end up doing is creating a timing leak through your memory access patterns. This can culminate in a timing vulnerability, but even if your data is too big to fit in a processor’s cache line (I dunno, Post-Quantum RSA keys?), there’s another risk to consider.
Virtual memory addresses are just beautiful lies. Where your data lives on the actual hardware memory is entirely up to the kernel. You can have two blobs with contiguous virtual memory addresses that live on separate memory pages, or even separate RAM chips (if you have multiple).
If you’re swapping pointers around, and they point to two different pieces of hardware, and one is slightly faster to read from than the other, you can introduce yet another timing attack through which pointer is being referenced by the processor.

If you’re swapping between X and Y before performing a calculation, where:
- X lives on RAM chip 1, which takes 3 ns to read
- Y lives on RAM chip 2, which takes 4 ns to read
…then the subsequent use of the swapped pointers reveals whether you’re operating on X or Y in the timing: It will take slightly longer to read from Y than from X.
The best way to mitigate this problem is to never design your software to have it in the first place. Don’t be clever on this one.
Constant-Time String Inequality Comparison
Sometimes you don’t just need to know if two strings are equal, you also need to know which one is larger than the other.
To accomplish this in constant-time, we need to maintain two state variables:
- gt (initialized to 0, will be set to 1 at some point if left > right)
- eq (initialized to 1, will be set to 0 at some point if left != right)
Endian-ness will dictate the direction our algorithm goes, but we’re going to perform two operations in each cycle:
- gt should be bitwise ORed with (eq AND ((right – left) right shifted 8 times)
- eq should be bitwise ANDed with ((right XOR left) – 1) right shifted 8 times
If right and left are ever different, eq will be set to 0.
If the first time they’re different the value for lefti is greater than the value for righti, then the subtraction will produce a negative number. Right shifting a negative number 8 places then bitwise ANDing the result with eq (which is only 1 until two bytes differ, and then 0 henceforth if they do) will result in a value for 1 with gt. Thus, if (righti – lefti) is negative, gt will be set to 1. Otherwise, it remains 0.
At the end of this loop, return (gt + gt + eq) – 1. This will result in the following possible values:
- left < right: -1
- left == right: 0
- left > right: 1
The arithmetic based on the possible values of gt and eq should be straightforward.
- Different (eq == 0) but not greater (gt == 0) means left < right, -1.
- Different (eq == 0) and greater (gt == 1) means left > right, 1.
- If eq == 1, no bytes ever differed, so left == right, 0.
A little endian implementation is as follows:
<?phpfunction str_compare(string $left, string $right): int{ $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } $gt = 0; $eq = 1; $i = $length; while ($i > 0) { --$i; $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $gt |= (($rightCharCode - $leftCharCode) >> 8) & $eq; $eq &= (($rightCharCode ^ $leftCharCode) -1) >> 8; } return ($gt + $gt + $eq) - 1;}
Demo for this function is available here.
Constant-Time Integer Multiplication
Multiplying two integers is one of those arithmetic operations that should be constant-time. But on many older processors, it isn’t.

Fortunately, there is a workaround. It involves an algorithm called Ancient Egyptian Multiplication in some places or Peasant Multiplication in others.
Multiplying two numbers 
- Determine the number of operations you need to perform. Generally, this is either known ahead of time or
.
- Set
to 0.
- Until the operation count reaches zero:
- If the lowest bit of
is set, add
to
.
- Left shift
by 1.
- Right shfit
by 1.
- If the lowest bit of
- Return
.
The main caveat here is that you want to use bitwise operators in step 3.1 to remove the conditional branch.
Rather than bundle example code in our blog post, please refer to the implementation in sodium_compat (a pure PHP polyfill for libsodium).
For big number libraries, implementing Karatsuba on top of this integer multiplying function should be faster than attempting to multiply bignums this way.
Constant-Time Integer Division
Although some cryptography algorithms call for integer division, division isn’t usually expected to be constant-time.
However, if you look up a division algorithm for unsigned integers with a remainder, you’ll likely encounter this algorithm, which is almost constant-time:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator if R ≥ D then R := R − D Q(i) := 1 endend
If we use the tricks we learned from implementing constant-time string inequality with constant-time conditional selection, we can implement this algorithm without timing leaks.
Our constant-time version of this algorithm looks like this:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator compared := ct_compare(R, D) -- Use constant-time inequality -- if R > D then compared == 1, swap = 1 -- if R == D then compared == 0, swap = 1 -- if R < D then compared == -1, swap = 0 swap := (1 - ((compared >> 31) & 1)) -- R' = R - D -- Q' = Q, Q = 1 Rprime := R - D Qprime := Q Qprime(i) := 1 -- The i'th bit is set to 1 -- Replace (R with R', Q with Q') if swap == 1 R = ct_select(swap, Rprime, R) Q = ct_select(swap, Qprime, Q)end
It’s approximately twice as slow as the original, but it’s constant-time.

Constant-Time Modular Inversion
Modular inversion is the calculation of 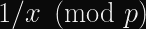
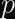
Daniel J. Bernstein and Bo-Yin Yang published a paper on fast constant-time GCD and Modular Inversion in 2019. The algorithm in question is somewhat straightforward to implement (although determining whether or not that implementation is safe is left as an exercise to the rest of us).
A simpler technique is to use Fermat’s Little Theorem: 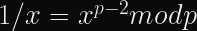
BearSSL provides an implementation (and accompanying documentation) for a constant-time modular inversion algorithm based on Binary GCD.
(In the future, I may update this section of this blog post with an implementation in PHP, using the GMP extension.)
Constant-Time Null-Byte Trimming
Shortly after this guide first went online, security researchers published the Raccoon Attack, which used a timing leak in the number of leading 0 bytes in the pre-master secret–combined with a lattice attack to solve the hidden number problem–to break TLS-DH(E).
To solve this, you need two components:
- A function that returns a slice of an array without timing leaks.
- A function that counts the number of significant bytes (i.e. ignores leading zero bytes, counts from the first non-zero byte).
A timing-safe array resize function needs to do two things:
- Touch every byte of the input array once.
- Touch every byte of the output array at least once, linearly. The constant-time division algorithm is useful here (to calculate x mod n for the output array index).
- Conditionally select between input[x] and the existing output[x_mod_n], based on whether x >= target size.
I’ve implemented this in my constant-time-js library:
Further Reading and Online Resources
If you’re at all interested in cryptographic side-channels, your hunger for knowledge probably won’t be sated by a single blog post. Here’s a collection of articles, papers, books, etc. worth reading.
- BearSSL’s Documentation on Constant-Time Code — A must-read for anyone interested in this topic
- Cryptographically Secure PHP Development — How to write secure cryptography in languages that cryptographers largely neglect
- CryptoCoding — A style guide for writing secure cryptography code in C (with example code!)
- CryptoGotchas — An overview of the common mistakes one can make when writing cryptography code (which is a much wider scope than side-channels)
- Meltdown and Spectre — Two vulnerabilities that placed side-channels in the scope of most of infosec that isn’t interested in cryptography
- Serious Cryptography — For anyone who lacks the background knowledge to fully understand what I’m talking about on this page
Errata
- 2020-08-27: The original version of this blog post incorrectly attributed Jacobian coordinate blinding to ECDSA hardening, rather than ECDH hardening. This error was brought to my attention by Thai Duong. Thanks Thai!
- 2020-08-27: Erin correctly pointed out that omitting memory access timing was a disservice to developers, who might not be aware of the risks involved. I’ve updated the post to call this risk out specifically (especially in the conditional select code, which some developers might try to implement with pointer swapping without knowing the risks involved). Thanks Erin!
I hope you find this guide to side-channels helpful.

Follow my blog for more Defense Against the Bark Arts posts in the future.
https://soatok.blog/2020/08/27/soatoks-guide-to-side-channel-attacks/
#asymmetricCryptography #constantTime #cryptography #ECDH #ECDSA #ellipticCurveCryptography #RSA #SecurityGuidance #sideChannels #symmetricCryptography
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Art by Khia.
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting
(at 50% probability) blocks.
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
you expect from AES.
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.This is because Grover’s quantum search algorithm can search
unsorted items in
time, which can be used to reduce the total number of possible secrets from
to
. This effectively cuts the security level, expressed in bits, in half.
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
(plaintext, key) pairs that produce any given ciphertext block.
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
times as many AES-256 keys as there are possible plaintext/ciphertexts. Keep this in mind for AES-GCM.
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
This is unacceptable!
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
: A number that must only be used once).
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
The deeper you look into AES-GCM’s design, the harder you will feel this sticker.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called. This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
This is often sold as an advantage: Reusingallows for better performance. However, it makes GCM brittle: Reusing a nonce allows an attacker to recover H and then forge messages forever. This is called the “forbidden attack”, and led to real world practical breaks.
Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.If we assume AES is well-behaved, we can deduce that there are approximately
different 256-bit keys that will map a single plaintext block to a single ciphertext block.
This is trivial to calculate. Simply divide the number of possible keys (
) by the number of possible block states (
) to yield the number of keys that produce a given ciphertext for a single block of plaintext:
.
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
.
This means there are approximately
independent keys that will map a given all-zero plaintext block to an arbitrarily chosen value of
(if we assume AES doesn’t have weird biases).
Credit: Harubaki
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection ofas a 128-bit pseudorandom function, rather than a 128-bit permutation. As a result, you an expect a collision with 50% probability after only
different keys are selected.
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a
collision risk. So that means our safety limit is actually
different AES keys before you have to worry about
reuse.
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of
different AES keys, you have to either accept the risk or stop using AES-GCM.
If you have a billion users (
), the safety limit is breached after
AES keys per user (approximately 262,000).
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.is used for block multiplication, and
(the value of
with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.
The arrow highlighted with green is HF.
It’s tempting to think that a reuse of
isn’t a concern because
will necessarily be randomized, which prevents an attacker from observing when
collides. It’s certainly true that the single-block collision risk discussed previously for
will almost certainly not also result in a collision for
. And since
isn’t reused unless a nonce is reused (which also leaks
directly), this might seem like a non-issue.
Art by Khia.
However, it’s straightforward to go from a condition of
reuse to an adaptive chosen-ciphertext attack.
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- Use your knowledge of
, the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of
for a given nonce.
- Calculate a new authentication tag for a chosen ciphertext using
and your candidate
value, then replay it into the target system.
While the blinding offered by XORing the final output with
is sufficient to stop
from being leaked directly, the protection is one-way.
Ergo, a collision in
is not sufficiently thwarted by
.
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
is
, and finding an untargeted collision requires being able to observe more than
different sessions, and somehow distinguish when
collides.
As a user, you know that after
different keys, you’ve crossed the safety boundary for avoiding
collisions. But as an attacker, you need
bites at the apple, not
. Additionally, you need some sort of oracle or distinguisher for when this happens.
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
is challenging to work with. You would need the computational and data storages of a major cloud service provider to even think about pulling the attack off.
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
bytes long, under a given (key, nonce) pair.
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
messages.
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atrandom nonces, which represents a collision probability of one in 4 billion.
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
I’m glad you asked!
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
messages (for the same collision probability as AES-GCM).
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography