Suppose you need to encrypt data between two peer-to-peer devices over an untrusted medium (i.e. the Internet), and you have an authenticated low-bandwidth channel that can be used to send and authenticate a few bytes (less than 100), but that channel isn’t itself encrypted (otherwise it’d be a chicken-and-egg problem).
Art by Swizz.
Aside: If it helps your mental image, you can pretend that the authenticated channel is a blockchain, if you want. You can squeeze a few bytes in there, and the data structure is verifiable, but everything you transmit is public. But the actual channel implementation isn’t important here; this is a thought experiment.

This was an unsolved problem in mathematics and cryptography until the 1970’s, when Whitfeld Diffie, Martin Hellman, and Ralph Merkle published the original Diffie-Hellman protocol and invented asymmetric (a.k.a. public-key) cryptography.

Modern cryptography uses a variant of the initial Diffie-Hellman protocol, defined over a mathematical structure called an Elliptic Curve. Thus, it is called Elliptic Curve Diffie Hellman (ECDH).

Note: I’m intentionally breaking from the mathematical orthodoxy in this blog post in the hopes that it’s more accessible to everyone outside the ivory tower. As a result, my definitions may lack precision, but I’m saving you from jargon.

Elliptic Curve Diffie-Hellman

Art by Swizz.
Without going into the nuts and bolts of ECDH (a subject of a future blog post!), this is basically what’s happening in layman’s (n.b. non-mathematician’s) terms:

1. You’ve got an elliptic curve, which satisfies some equation. There are many different curve shapes. One example is , where A and B are integer constants. (This example is called a Montgomery curve.)
2. You’ve got a field parameter, . This is usually a prime number. (If it isn’t, and you aren’t a cryptographer, you probably want to run away from it.)
3. You’ve got a generator, (which is some specific point on the curve), which transforms the whole shebang into a thing called a “group” which has a thing called an “order” (which in turn is an integer of value ). The fact that this thing is a “group” at all is what makes Diffie-Hellman possible.
   You don’t need to worry about what these things even are, because I’m not delving into the underlying mathematics (nuts and bolts) at all. But if I omit them, the pedants complain, so for the sake of completeness: Here you go.

   Take a mathematics course that covers Galois theory if you want the inside scoop on what the hell those things are. But for now, if you’re lost, just know that you have some special parameters/properties that have specific names and don’t worry about what they mean.

These parameters are meant to be public, and preferably hard-coded. When they’re not, you get CVE-2020-0601.

Each participant (simplest case: there are only two) will need two keys to agree on a shared secret: Their secret key and its corresponding public key.

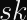
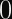
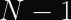
To calculate a secret key (), a random integer is selected between and (inclusive).

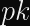
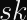
To calculate a public key (), the generator is added to itself times.

This sounds trivial and slow, but Point Addition in an Elliptic Curve is a peculiar operation, and the process is a form of multiplication. Strictly speaking, this is multiplication.

I will cover this in detail in a future blog post. For now, just know that you’re multiplying a number (“scalar”) by a point, and that the underlying mechanics of multiplication (which is just adding a point to itself some number of times) involves point addition, which is very weird if you’re not a cryptographer.

We can delve into the complexity later, just keep in mind you’re calculating 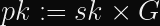to get a public key from a secret key.

It bears emphasizing: Each participant does this.

The orthodox characters for describing cryptographic protocols are Alice and Bob. Alice wants to talk to Bob, Bob wants to talk to Alice, and they want no one else to successfully interfere in their communication.

Alice has .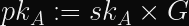

Bob has .

If they perform one calculation, they can derive a shared secret while only sharing their public keys over the authenticated channel: Multiply their secret key by the other party’s public key.

Alice performs .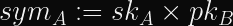

Bob performs .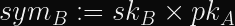

Since multiplication is commutative, they both arrive at the same shared value, despite only transmitting public keys. Someone snooping on the authenticated channel cannot, with current technology, recover the shared secret or either party’s secret key.

With some caveats, of course:

Which Public Key Do I AKE?

We handwaved this away earlier, but an authenticated channel is critically necessary to transmit public keys. Otherwise, an active attacker can just substitute public keys and sit in the middle, with neither party realizing they’re talking to a middleman.
There’s a spy sappin’ my sentry!
This turns out to be a bit tricky, but not intractable.

TLS (the S in HTTPS) uses long-term digital signature algorithms and chains of digital signatures from a short list of trusted Root Certificate Authorities to authenticate the identity of the server you’re talking to, and then that server’s digital signature public key (signed by an intermediary Certificate Authority) is used to sign ECDH public keys.

I briefly mentioned this in the post about Authenticated Key Exchanges.

Your Curve is Invalid

This is less of a problem with newer elliptic curves, but for a very long time, public keys were transmitted as a pair of 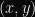coordinates.

Earlier, we mentioned that both parties have to agree on some curve parameters. But in protocols where you send arbitrary points, an attacker could send a point on a different curve to leak bits about the target’s secret key.

The standard mitigation is to solve the elliptic curve equation and verify that the coordinates of the point satisfy the chosen elliptic curve parameters.

Modern protocols only send a single coordinate, and possibly a single bit to signify whether the other coordinate is positive or negative (either 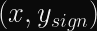or ).

This is called point compression and used to be patented (until 2018). Since the patent has expired, protocols should investigate adopting point compression if they can’t just switch to secure curves.

Optimus Anti-Primes

Since multiplication is commutative, it’s possible that two unrelated pairs of participants could perform an ECDH step and agree on the same shared secret.

This is true for the same reason that 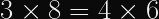, and because your secret key is a random integer.

For this reason, it’s generally unwise to use raw ECDH outputs as encryption keys. Instead, you want to use a cryptographic hash function over the ECDH output and each participants’ public keys to guarantee your symmetric session key is distinct from other pairs.

Whose Time Is It Anyway?

In addition to what I’ve described above, all of the algorithms involved need to perform in constant-time. Any failure to do so will result in your secret key leaking to attackers through network traffic timing (and other side-channels).

I’ll explore the engineering that goes into constant-time implementations in a future blog post.

My hope in writing this page is that anyone without a mathematics background can walk away with a basic intuition for how ECDH works and how dangerous cryptography is when left to the hands of amateurs.

If you find yourself faced with a scenario like we discussed here, you want to use a well-studied Authenticated Key Exchange instead of rolling your own.

If you have to roll your own, try to wrap or take inspiration from libsodium.

https://soatok.blog/2020/04/21/elliptic-curve-diffie-hellman-for-humans-and-furries/

#cryptography #ECDH

Dhole Moments

2020-04-21 12:25:46

Authenticated Key Exchanges are an interesting and important building block in any protocol that aims to allow people to communicate privately over an untrusted medium (i.e. the Internet).

What’s an AKE?

At their core, Authenticated Key Exchanges (AKEs for short) combine two different classes of protocol.

1. An authentication mechanism, such as a MAC or a digital signature.
2. Key encapsulation, usually through some sort of Diffie-Hellman.

A simple example of an AKE is the modern TLS handshake, which uses digital signatures (X.509 certificates signed by certificate authorities) to sign ephemeral Elliptic Curve Diffie-Hellman (ECDH) public keys, which is then used to derive a shared secret to encrypt and authenticate network traffic.

I guess I should say “simple” with scare quotes. Cryptography is very much a “devil’s in the details” field, because my above explanation didn’t even encapsulate mutual-auth TLS or the underlying machinery of protocol negotiation. (Or the fact that non-forward-secret ciphersuites can be selected.)

AKEs get much more complicated, the more sophisticated your threat model becomes.

For example: Signal’s X3DH and Double Ratchet protocols are components of a very sophisticated AKE. Learn more about them here.

The IETF is working to standardize their own approach, called Messaging Layer Security (MLS), which uses a binary tree of ECDH handshakes to manage state and optimize group operations (called TreeKEM). You can learn more about IETF MLS here.

Password AKEs

Recently, a collection of cryptographers at the IETF’s Crypto Research Forum Group (CFRG) decided to hammer on a series of proposed Password-Authenticated Key Exchange (PAKE) protocols.

PAKEs come in two flavors: Balanced (mutually authenticated) and augmented (one side is a prover, the other is a verifier). Balanced PAKEs are good for encrypted tunnels where you control both endpoints (e.g. WiFi networks), whereas Augmented PAKEs are great for eliminating the risk of password theft in client-server applications, if the server gets hacked.

Ultimately, the CFRG settled on one balanced PAKE (CPace) and one augmented PAKE (OPAQUE).

Consequently, cryptographer Filippo Valsorda managed to implement CPace in 125 lines of Go, using Ristretto255.

I implemented the CPace PAKE yesterday with Go and ristretto255, and it felt like cheating.

📦 https://t.co/Q0kI19JOPY 📦

125 lines of code! Really happy with it and it was a lot of fun.

— Filippo Valsorda (@FiloSottile) March 29, 2020

Why So Complicated?

At the end of the day, an AKE is just a construction that combines key encapsulation with an authentication mechanism.

But how you combine these components together can vary wildly!

Some AKE designs (i.e. Dragonfly, in WPA3) are weaker than others; even if only in the sense of being difficult to implement in constant-time.

The reason there’s so many is that cryptographers tend to collectively decide which algorithms to recommend for standardization.

(n.b. There are a lot more block ciphers than DES, Blowfish, and AES to choose from! But ask a non-cryptographer to name five block ciphers and they’ll probably struggle.)

https://soatok.blog/2020/04/21/authenticated-key-exchanges/

#ake #authenticatedKeyExchange #cryptography #ECDH

If you’re ever tasked with implementing a cryptography feature–whether a high-level protocol or a low-level primitive–you will have to take special care to ensure you’re not leaking secret information through side-channels.

The descriptions of algorithms you learn in a classroom or textbook are not sufficient for real-world use. (Yes, that means your toy RSA implementation based on GMP from your computer science 101 class isn’t production-ready. Don’t deploy it.)

But what are these elusive side-channels exactly, and how do you prevent them? And in cases where you cannot prevent them, how can you mitigate the risk to your users?

Art by Swizz.

Contents

• Cryptographic Side-Channels
  
  • Timing Leaks
  • Power Usage
  • Electromagnetic Emissions

  
  

• Side-Channel Prevention and Mitigation
  
  • Prevention vs. Mitigation
  • What is Constant-Time?
  • Malicious Environments and Algorithmic Constant-Time
  • Mitigation with Blinding Techniques

  
  

• Design Patterns for Algorithmic Constant-Time Code
  
  • Constant-Time String Comparison
  • Alternative: “Double HMAC” String Comparison
  • Constant-Time Conditional Select
  • Constant-Time String Inequality Comparison
  • Constant-Time Integer Multiplication
  • Constant-Time Integer Division
  • Constant-Time Modular Inversion
  • Constant-Time Null-Byte Trimming

  
  

• Further Reading and Online Resources
• Errata

Cryptographic Side-Channels

The concept of a side-channel isn’t inherently cryptographic, as Taylor Hornby demonstrates, but a side-channel can be a game over vulnerability in a system meant to maintain confidentiality (even if only for its cryptography keys).

Cryptographic side-channels allow an attacker to learn secret data from your cryptography system. To accomplish this, the attacker doesn’t necessarily study the system’s output (i.e. ciphertext); instead, they observe some other measurement, such as how much time or power was spent performing an operation, or what kind of electromagnetic radiation was emitted.

Important: While being resistant to side-channels is a prerequisite for implementations to be secure, it isn’t in and of itself sufficient for security. The underlying design of the primitives, constructions, and high-level protocols needs to be secure first, and that requires a clear and specific threat model for what you’re building.

Constant-time ECDSA doesn’t help you if you reuse k-values like it’s going out of style, but variable-time ECDSA still leaks your secret key to anyone who cares to probe your response times. Secure cryptography is very demanding.

Art by Riley.

Timing Leaks

Timing side-channels leak secrets through how much time it takes for an operation to complete.

There are many different flavors of timing leakage, including:

• Fast-failing comparison functions (memcmp() in C)
• Cache-timing vulnerabilities (e.g. software AES)
• Memory access patterns
• Conditional branches controlled by secrets

The bad news about timing leaks is that they’re almost always visible to an attacker over the network (including over the Internet (PDF)).

The good news is that most of them can be prevented or mitigated in software.

Art by Kyume.

Power Usage

Different algorithms or processor operations may require different amounts of power.

For example, squaring a large number may take less power than multiplying two different large numbers. This observation has led to the development of power analysis attacks against RSA.

Power analysis is especially relevant for embedded systems and smart cards, which are easier to extract a meaningful signal from than your desktop computer.

Some information leakage through power usage can be prevented through careful engineering (for example: BearSSL, which uses Montgomery multiplication instead of square-and-multiply).

But that’s not always an option, so generally these risks are mitigated.

My reaction when I first learned of power leaks: WATT (Art by Swizz)

Electromagnetic Emissions

https://youtu.be/CCgSGZ7S-BQ

Your computer is a reliable source of electromagnetic emissions (such as radio waves). Some of these emissions may reveal information about your cryptographic secrets, especially to an attacker with physical proximity to your device.

The good news is that research into EM emission side-channels isn’t as mature as side-channels through timing leaks or power usage. The bad news is that mitigations for breakthroughs will generally require hardware (e.g. electromagnetic shielding).

Aren’t computers terrifying? (Art by Swizz)

Side-Channel Prevention and Mitigation

Now that we’ve established a rough sense of some of the types of side-channels that are possible, we can begin to identify what causes them and aspire to prevent the leaks from happening–and where we can’t, to mitigate the risk to a reasonable level.

Note: To be clear, I didn’t cover all of the types of side-channels.

Prevention vs. Mitigation

Preventing a side-channel means eliminating the conditions that allow the information leak to occur in the first place. For timing leaks, this means making all algorithms constant-time.

There are entire classes of side-channel leaks that aren’t possible or practical to mitigate in software. When you encounter one, the best you can hope to do is mitigate the risk.

Ideally, you want to make the attack more expensive to pull off than the reward an attacker will gain from it.

What is Constant-Time?

https://www.youtube.com/watch?v=ZD_H1ePLylA

When an implementation is said to be constant-time, what we mean is that the execution time of the code is not a function of its secret inputs.

Vulnerable AES uses table look-ups to implement the S-Box. Constant-time AES is either implemented in hardware, or is bitsliced.

Malicious Environments and Algorithmic Constant-Time

One of the greatest challenges with writing constant-time code is distinguishing between algorithmic constant-time and provably constant-time. The main difference between the two is that you cannot trust your compiler (especially a JIT compiler), which may attempt to optimize your code in a way that reintroduces the side-channel you aspired to remove.

A sufficiently advanced compiler optimization is indistinguishable from an adversary.

John Regehr, possibly with apologies to Arthur C. Clarke

For compiled languages, this is a tractable but expensive problem to solve: You simply have to formally verify everything from the source code to the compiler to the silicon chips that the code will be deployed on, and then audit your supply chain to prevent malicious tampering from going undetected.

For interpreted languages (e.g. PHP and JavaScript), this formal verification strategy isn’t really an option, unless you want to formally verify the runtime that interprets scripts and prove that the operations remain constant-time on top of all the other layers of distrust.

Is this level of paranoia really worth the effort?

For our cases, anyway! (Art by Khia.)

For that reason, we’re going to assume that algorithmic constant-time is adequate for the duration of this blog post.

If your threat model prevents you from accepting this assumption, feel free to put in the extra effort yourself and tell me how it goes. After all, as a furry who writes blog posts in my spare time for fun, I don’t exactly have the budget for massive research projects in formal verification.

Mitigation with Blinding Techniques

The best mitigation for some side-channels is called blinding: Obfuscating the inputs with some random data, then deobfuscating the outputs with the same random data, such that your keys are not revealed.

Two well-known examples include RSA decryption and Elliptic Curve Diffie-Hellman. I’ll focus on the latter, since it’s not as widely covered in the literature (although several cryptographers I’ve talked with were somehow knowledgeable about it; I suspect gatekeeping is involved).

Blinded ECDH Key Exchange

In typical ECDH implementations, you will convert a point on a Weierstrass curve to a Jacobian coordinate system .

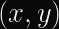
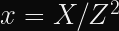
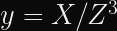
The exact conversion formula is (, ). The conversion almost makes intuitive sense.

Where does come from though?

Art by circuitslime

It turns out, the choice for 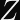is totally arbitrary. Libraries typically set it equal to 1 (for best performance), but you can also set it to a random number. (You cannot set it to 0, however, for obvious reasons.)

Choosing a random number means the calculations performed over Jacobian coordinates will be obscured by a randomly chosen factor 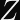(and thus, if is only used once per scalar multiplication, the bitwise signal the attackers rely on will be lost).

Blinding techniques are cool. (Art by Khia.)

I think it’s really cool how one small tweak to the runtime of an algorithm can make it significantly harder to attack.

Design Patterns for Algorithmic Constant-Time Code

Mitigation techniques are cool, but preventing side-channels is a better value-add for most software.

To that end, let’s look at some design patterns for constant-time software. Some of these are relatively common; others, not so much.

Art by Scout Pawfoot.

If you prefer TypeScript / JavaScirpt, check out Soatok’s constant-time-js library on Github / NPM.

Constant-Time String Comparison

Rather than using string comparison (== in most programming languages, memcmp() in C), you want to compare cryptographic secrets and/or calculated integrity checks with a secure compare algorithm, which looks like this:

1. Initialize a variable (let’s call it D) to zero.
2. For each byte of the two strings:
   
   1. Calculate (lefti XOR righti)
   2. Bitwise OR the current value of D with the result of the XOR, store the output in D

   
   

3. When the loop has concluded, D will be equal to 0 if and only if the two strings are equal.

In code form, it looks like this:
<?phpfunction ct_compare(string $left, string $right): bool{ $d = 0; $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { return false; // Lengths differ } for ($i = 0; $i < $length; ++$i) { $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $d |= ($leftCharCode ^ $rightCharCode); } return $d === 0;}
In this example, I’m using PHP’s unpack() function to avoid cache-timing leaks with ord() and chr(). Of course, you can simply use hash_equals() instead of writing it yourself (PHP 5.6.0+).

Alternative: “Double HMAC” String Comparison

If the previous algorithm won’t work (i.e. because you’re concerned your JIT compiler will optimize it away), there is a popular alternative to consider. It’s called “Double HMAC” because it was traditionally used with Encrypt-Then-HMAC schemes.

The algorithm looks like this:

1. Generate a random 256-bit key, K. (This can be cached between invocations, but it should be unpredictable.)
2. Calculate HMAC-SHA256(K, left).
3. Calculate HMAC-SHA256(K, right).
4. Return true if the outputs of step 2 and 3 are equal.

This is provably secure, so long as HMAC-SHA256 is a secure pseudo-random function and the key K is unknown to the attacker.

In code form, the Double HMAC compare function looks like this:

<?phpfunction hmac_compare(string $left, string $right): bool{ static $k = null; if (!$k) $k = random_bytes(32); return ( hash_hmac('sha256', $left, $k) === hash_hmac('sha256', $right, $k) );}

Constant-Time Conditional Select

I like to imagine a conversation between a cryptography engineer and a Zen Buddhist, that unfolds like so:

• CE: “I want to eliminate branching side-channels from my code.”
• ZB: “Then do not have branches in your code.”

And that is precisely what we intend to do with a constant-time conditional select: Eliminate branches by conditionally returning between one of two strings, without an IF statement.

Mind. Blown. (Art by Khia.)

This isn’t as tricky as it sounds. We’re going to use XOR and two’s complement to achieve this.

The algorithm looks like this:

1. Convert the selection bit (TRUE/FALSE) into a mask value (-1 for TRUE, 0 for FALSE). Bitwise, -1 looks like 111111111…1111111111, while 0 looks like 00000000…00000000.
2. Copy the right string into a buffer, call it tmp.
3. Calculate left XOR right, call it x.
4. Return (tmp XOR (x AND mask)).

Once again, in code this algorithm looks like this:
<?phpfunction ct_select( bool $returnLeft, string $left, string $right): string { $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } // Mask byte $mask = (-$returnLeft) & 0xff; // X $x = (string) ($left ^ $right); // Output = Right XOR (X AND Mask) $output = ''; for ($i = 0; $i < $length; $i++) { $rightCharCode = unpack('C', $right[$i])[1]; $xCharCode = unpack('C', $x[$i])[1]; $output .= pack( 'C', $rightCharCode ^ ($xCharCode & $mask) ); } return $output;}
You can test this code for yourself here. The function was designed to read intuitively like a ternary operator.

A Word of Caution on Cleverness

In some languages, it may seem tempting to use the bitwise trickery to swap out pointers instead of returning a new buffer. But do not fall for this Siren song.

If, instead of returning a new buffer, you just swap pointers, what you’ll end up doing is creating a timing leak through your memory access patterns. This can culminate in a timing vulnerability, but even if your data is too big to fit in a processor’s cache line (I dunno, Post-Quantum RSA keys?), there’s another risk to consider.

Virtual memory addresses are just beautiful lies. Where your data lives on the actual hardware memory is entirely up to the kernel. You can have two blobs with contiguous virtual memory addresses that live on separate memory pages, or even separate RAM chips (if you have multiple).

If you’re swapping pointers around, and they point to two different pieces of hardware, and one is slightly faster to read from than the other, you can introduce yet another timing attack through which pointer is being referenced by the processor.

It’s timing leaks all the ways down! (Art by Swizz)

If you’re swapping between X and Y before performing a calculation, where:

• X lives on RAM chip 1, which takes 3 ns to read
• Y lives on RAM chip 2, which takes 4 ns to read

…then the subsequent use of the swapped pointers reveals whether you’re operating on X or Y in the timing: It will take slightly longer to read from Y than from X.

The best way to mitigate this problem is to never design your software to have it in the first place. Don’t be clever on this one.

Constant-Time String Inequality Comparison

Sometimes you don’t just need to know if two strings are equal, you also need to know which one is larger than the other.

To accomplish this in constant-time, we need to maintain two state variables:

1. gt (initialized to 0, will be set to 1 at some point if left > right)
2. eq (initialized to 1, will be set to 0 at some point if left != right)

Endian-ness will dictate the direction our algorithm goes, but we’re going to perform two operations in each cycle:

1. gt should be bitwise ORed with (eq AND ((right – left) right shifted 8 times)
2. eq should be bitwise ANDed with ((right XOR left) – 1) right shifted 8 times

If right and left are ever different, eq will be set to 0.

If the first time they’re different the value for lefti is greater than the value for righti, then the subtraction will produce a negative number. Right shifting a negative number 8 places then bitwise ANDing the result with eq (which is only 1 until two bytes differ, and then 0 henceforth if they do) will result in a value for 1 with gt. Thus, if (righti – lefti) is negative, gt will be set to 1. Otherwise, it remains 0.

At the end of this loop, return (gt + gt + eq) – 1. This will result in the following possible values:

• left < right: -1
• left == right: 0
• left > right: 1

The arithmetic based on the possible values of gt and eq should be straightforward.

• Different (eq == 0) but not greater (gt == 0) means left < right, -1.
• Different (eq == 0) and greater (gt == 1) means left > right, 1.
• If eq == 1, no bytes ever differed, so left == right, 0.

A little endian implementation is as follows:
<?phpfunction str_compare(string $left, string $right): int{ $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } $gt = 0; $eq = 1; $i = $length; while ($i > 0) { --$i; $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $gt |= (($rightCharCode - $leftCharCode) >> 8) & $eq; $eq &= (($rightCharCode ^ $leftCharCode) -1) >> 8; } return ($gt + $gt + $eq) - 1;}
Demo for this function is available here.

Constant-Time Integer Multiplication

Multiplying two integers is one of those arithmetic operations that should be constant-time. But on many older processors, it isn’t.

Of course there’s a microarchitecture timing leak! (Art by Khia.)

Fortunately, there is a workaround. It involves an algorithm called Ancient Egyptian Multiplication in some places or Peasant Multiplication in others.

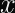
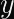
Multiplying two numbers and this way looks like this:

1. Determine the number of operations you need to perform. Generally, this is either known ahead of time or .
2. Set to 0.
3. Until the operation count reaches zero:
   
   1. If the lowest bit of is set, add to .
   2. Left shift by 1.
   3. Right shfit by 1.

   
   

4. Return .

The main caveat here is that you want to use bitwise operators in step 3.1 to remove the conditional branch.

Rather than bundle example code in our blog post, please refer to the implementation in sodium_compat (a pure PHP polyfill for libsodium).

For big number libraries, implementing Karatsuba on top of this integer multiplying function should be faster than attempting to multiply bignums this way.

Constant-Time Integer Division

Although some cryptography algorithms call for integer division, division isn’t usually expected to be constant-time.

However, if you look up a division algorithm for unsigned integers with a remainder, you’ll likely encounter this algorithm, which is almost constant-time:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator if R ≥ D then R := R − D Q(i) := 1 endend
If we use the tricks we learned from implementing constant-time string inequality with constant-time conditional selection, we can implement this algorithm without timing leaks.

Our constant-time version of this algorithm looks like this:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator compared := ct_compare(R, D) -- Use constant-time inequality -- if R > D then compared == 1, swap = 1 -- if R == D then compared == 0, swap = 1 -- if R < D then compared == -1, swap = 0 swap := (1 - ((compared >> 31) & 1)) -- R' = R - D -- Q' = Q, Q = 1 Rprime := R - D Qprime := Q Qprime(i) := 1 -- The i'th bit is set to 1 -- Replace (R with R', Q with Q') if swap == 1 R = ct_select(swap, Rprime, R) Q = ct_select(swap, Qprime, Q)end
It’s approximately twice as slow as the original, but it’s constant-time.

(Art by Khia.)

Constant-Time Modular Inversion

Modular inversion is the calculation of 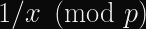for some prime . This is used in a lot of places, but especially in elliptic curve cryptography and RSA.

Daniel J. Bernstein and Bo-Yin Yang published a paper on fast constant-time GCD and Modular Inversion in 2019. The algorithm in question is somewhat straightforward to implement (although determining whether or not that implementation is safe is left as an exercise to the rest of us).

A simpler technique is to use Fermat’s Little Theorem: 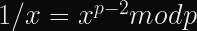for some prime . This only works with prime fields, and is slower than a Binary GCD (which isn’t [i]necessarily constant-time, as OpenSSL discovered).

BearSSL provides an implementation (and accompanying documentation) for a constant-time modular inversion algorithm based on Binary GCD.

(In the future, I may update this section of this blog post with an implementation in PHP, using the GMP extension.)

Constant-Time Null-Byte Trimming

Shortly after this guide first went online, security researchers published the Raccoon Attack, which used a timing leak in the number of leading 0 bytes in the pre-master secret–combined with a lattice attack to solve the hidden number problem–to break TLS-DH(E).

To solve this, you need two components:

1. A function that returns a slice of an array without timing leaks.
2. A function that counts the number of significant bytes (i.e. ignores leading zero bytes, counts from the first non-zero byte).

A timing-safe array resize function needs to do two things:

1. Touch every byte of the input array once.
2. Touch every byte of the output array at least once, linearly. The constant-time division algorithm is useful here (to calculate x mod n for the output array index).
3. Conditionally select between input[x] and the existing output[x_mod_n], based on whether x >= target size.

I’ve implemented this in my constant-time-js library:

• resize.ts
• trim.ts

Further Reading and Online Resources

If you’re at all interested in cryptographic side-channels, your hunger for knowledge probably won’t be sated by a single blog post. Here’s a collection of articles, papers, books, etc. worth reading.

• BearSSL’s Documentation on Constant-Time Code — A must-read for anyone interested in this topic
• Cryptographically Secure PHP Development — How to write secure cryptography in languages that cryptographers largely neglect
• CryptoCoding — A style guide for writing secure cryptography code in C (with example code!)
• CryptoGotchas — An overview of the common mistakes one can make when writing cryptography code (which is a much wider scope than side-channels)
• Meltdown and Spectre — Two vulnerabilities that placed side-channels in the scope of most of infosec that isn’t interested in cryptography
• Serious Cryptography — For anyone who lacks the background knowledge to fully understand what I’m talking about on this page

Errata

• 2020-08-27: The original version of this blog post incorrectly attributed Jacobian coordinate blinding to ECDSA hardening, rather than ECDH hardening. This error was brought to my attention by Thai Duong. Thanks Thai!
• 2020-08-27: Erin correctly pointed out that omitting memory access timing was a disservice to developers, who might not be aware of the risks involved. I’ve updated the post to call this risk out specifically (especially in the conditional select code, which some developers might try to implement with pointer swapping without knowing the risks involved). Thanks Erin!

I hope you find this guide to side-channels helpful.

Thanks for reading!

Follow my blog for more Defense Against the Bark Arts posts in the future.

https://soatok.blog/2020/08/27/soatoks-guide-to-side-channel-attacks/

#asymmetricCryptography #constantTime #cryptography #ECDH #ECDSA #ellipticCurveCryptography #RSA #SecurityGuidance #sideChannels #symmetricCryptography

Dhole Moments

2020-05-13 10:00:22

If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.

I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.

This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.

To be clear: This is solely my opinion and not representative of any company or academic institution.

What is AES-GCM?

AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.

In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.

What is AES?

The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.

Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.

AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.

As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.

This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)

Why AES Sucks

Art by Khia.

Side-Channels

The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).

There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.

The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.

Block Size

AES-128 is considered by experts to have a security level of 128 bits.

Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.

However, the AES block size is only 128 bits!

That might not sound like a big deal, but it severely limits the constructions you can create out of AES.

Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.

This means you expect a collision after encrypting (at 50% probability) blocks.

When you start getting collisions, you can break CBC mode, as this video demonstrates:

https://www.youtube.com/watch?v=v0IsYNDMV7A

This is significantly smaller than the you expect from AES.

Post-Quantum Security?

With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.

This is because Grover’s quantum search algorithm can search unsorted items in time, which can be used to reduce the total number of possible secrets from to . This effectively cuts the security level, expressed in bits, in half.

Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.

But remember, even AES-256 operates on 128-bit blocks.

Consequently, for AES-256, there should be approximately (plaintext, key) pairs that produce any given ciphertext block.

Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)

Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are times as many AES-256 keys as there are possible plaintext/ciphertexts. Keep this in mind for AES-GCM.

This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.

This would not be nearly as much of a problem if AES’s block size was 256 bits.

Real-World Example: Signal

The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.

Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.

Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.

The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).

Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.

Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.

However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.

This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.

This is unacceptable!

What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.

As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.

Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.

Why AES-GCM Sucks Even More

AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.

AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:

1. The plaintext message.
2. The encryption key.
3. A nonce (: A number that must only be used once).
4. Optional additional data which will be authenticated but not encrypted.

The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.

Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.

That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.

The deeper you look into AES-GCM’s design, the harder you will feel this sticker.

GHASH Brittleness

The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called . This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
This is often sold as an advantage: Reusing allows for better performance. However, it makes GCM brittle: Reusing a nonce allows an attacker to recover H and then forge messages forever. This is called the “forbidden attack”, and led to real world practical breaks.

Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.

ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.

While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.

Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.

H Reuse and Multi-User Security

If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.

If we assume AES is well-behaved, we can deduce that there are approximately different 256-bit keys that will map a single plaintext block to a single ciphertext block.

This is trivial to calculate. Simply divide the number of possible keys () by the number of possible block states () to yield the number of keys that produce a given ciphertext for a single block of plaintext: .

Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately .

This means there are approximately independent keys that will map a given all-zero plaintext block to an arbitrarily chosen value of (if we assume AES doesn’t have weird biases).

Credit: Harubaki

“Why Does This Matter?”

It means that, with keys larger than 128 bits, you can model the selection of as a 128-bit pseudorandom function, rather than a 128-bit permutation. As a result, you an expect a collision with 50% probability after only different keys are selected.

Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.

But 50% isn’t good enough for cryptographic security.

In most real-world systems, we target a collision risk. So that means our safety limit is actually different AES keys before you have to worry about reuse.

This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of different AES keys, you have to either accept the risk or stop using AES-GCM.

If you have a billion users (), the safety limit is breached after AES keys per user (approximately 262,000).

“What Good is H Reuse for Attackers if HF differs?”

There are two numbers used in AES-GCM that are derived from the AES key. is used for block multiplication, and (the value of with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.

The arrow highlighted with green is HF.

It’s tempting to think that a reuse of isn’t a concern because will necessarily be randomized, which prevents an attacker from observing when collides. It’s certainly true that the single-block collision risk discussed previously for will almost certainly not also result in a collision for . And since isn’t reused unless a nonce is reused (which also leaks directly), this might seem like a non-issue.

Art by Khia.

However, it’s straightforward to go from a condition of reuse to an adaptive chosen-ciphertext attack.

1. Intercept multiple valid ciphertexts.
   
   • e.g. Multiple JWTs encrypted with {"alg":"A256GCM"}

   
   

2. Use your knowledge of , the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of for a given nonce.
3. Calculate a new authentication tag for a chosen ciphertext using and your candidate value, then replay it into the target system.

While the blinding offered by XORing the final output with is sufficient to stop from being leaked directly, the protection is one-way.

Ergo, a collision in is not sufficiently thwarted by .

“How Could the Designers Have Prevented This?”

The core issue here is the AES block size, again.

If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.

However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.

NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).

“Why Isn’t This a Vulnerability?”

There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.

Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).

With AES-GCM, the expected distance between collisions in is , and finding an untargeted collision requires being able to observe more than different sessions, and somehow distinguish when collides.

As a user, you know that after different keys, you’ve crossed the safety boundary for avoiding collisions. But as an attacker, you need bites at the apple, not . Additionally, you need some sort of oracle or distinguisher for when this happens.

We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide is challenging to work with. You would need the computational and data storages of a major cloud service provider to even think about pulling the attack off.

Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.

Short Nonces

Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.

(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)

If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.

1. Message Length Limit: AES-GCM can be used to encrypt messages up to bytes long, under a given (key, nonce) pair.
2. Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after messages.
   However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM at random nonces, which represents a collision probability of one in 4 billion.

These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.

Random Key Robustness

Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).

You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.

Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.

Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.

Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.

This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)

Better-Designed Algorithms

You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”

I’m glad you asked!

XChaCha20-Poly1305

For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.

• ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
• ChaCha20 is ChaCha with 20 rounds.
• XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about messages (for the same collision probability as AES-GCM).
• Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
• XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.

For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.

However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.

The Gimli Permutation

For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.

Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.

Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.

Closing Remarks

Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.

Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.

Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.

My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.

We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.

Change Log

• 2021-10-26: Added section on H Reuse and Multi-User Security.

https://soatok.blog/2020/05/13/why-aes-gcm-sucks/

#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography

Authenticated Key Exchanges are an interesting and important building block in any protocol that aims to allow people to communicate privately over an untrusted medium (i.e. the Internet).

What’s an AKE?

At their core, Authenticated Key Exchanges (AKEs for short) combine two different classes of protocol.

1. An authentication mechanism, such as a MAC or a digital signature.
2. Key encapsulation, usually through some sort of Diffie-Hellman.

A simple example of an AKE is the modern TLS handshake, which uses digital signatures (X.509 certificates signed by certificate authorities) to sign ephemeral Elliptic Curve Diffie-Hellman (ECDH) public keys, which is then used to derive a shared secret to encrypt and authenticate network traffic.

I guess I should say “simple” with scare quotes. Cryptography is very much a “devil’s in the details” field, because my above explanation didn’t even encapsulate mutual-auth TLS or the underlying machinery of protocol negotiation. (Or the fact that non-forward-secret ciphersuites can be selected.)

AKEs get much more complicated, the more sophisticated your threat model becomes.

For example: Signal’s X3DH and Double Ratchet protocols are components of a very sophisticated AKE. Learn more about them here.

The IETF is working to standardize their own approach, called Messaging Layer Security (MLS), which uses a binary tree of ECDH handshakes to manage state and optimize group operations (called TreeKEM). You can learn more about IETF MLS here.

Password AKEs

Recently, a collection of cryptographers at the IETF’s Crypto Research Forum Group (CFRG) decided to hammer on a series of proposed Password-Authenticated Key Exchange (PAKE) protocols.

PAKEs come in two flavors: Balanced (mutually authenticated) and augmented (one side is a prover, the other is a verifier). Balanced PAKEs are good for encrypted tunnels where you control both endpoints (e.g. WiFi networks), whereas Augmented PAKEs are great for eliminating the risk of password theft in client-server applications, if the server gets hacked.

Ultimately, the CFRG settled on one balanced PAKE (CPace) and one augmented PAKE (OPAQUE).

Consequently, cryptographer Filippo Valsorda managed to implement CPace in 125 lines of Go, using Ristretto255.

I implemented the CPace PAKE yesterday with Go and ristretto255, and it felt like cheating.

📦 https://t.co/Q0kI19JOPY 📦

125 lines of code! Really happy with it and it was a lot of fun.

— Filippo Valsorda (@FiloSottile) March 29, 2020

Why So Complicated?

At the end of the day, an AKE is just a construction that combines key encapsulation with an authentication mechanism.

But how you combine these components together can vary wildly!

Some AKE designs (i.e. Dragonfly, in WPA3) are weaker than others; even if only in the sense of being difficult to implement in constant-time.

The reason there’s so many is that cryptographers tend to collectively decide which algorithms to recommend for standardization.

(n.b. There are a lot more block ciphers than DES, Blowfish, and AES to choose from! But ask a non-cryptographer to name five block ciphers and they’ll probably struggle.)

https://soatok.blog/2020/04/21/authenticated-key-exchanges/

#ake #authenticatedKeyExchange #cryptography #ECDH

Dhole Moments

2020-04-21 12:25:46

Authenticated Key Exchanges are an interesting and important building block in any protocol that aims to allow people to communicate privately over an untrusted medium (i.e. the Internet).

What’s an AKE?

At their core, Authenticated Key Exchanges (AKEs for short) combine two different classes of protocol.

1. An authentication mechanism, such as a MAC or a digital signature.
2. Key encapsulation, usually through some sort of Diffie-Hellman.

A simple example of an AKE is the modern TLS handshake, which uses digital signatures (X.509 certificates signed by certificate authorities) to sign ephemeral Elliptic Curve Diffie-Hellman (ECDH) public keys, which is then used to derive a shared secret to encrypt and authenticate network traffic.

I guess I should say “simple” with scare quotes. Cryptography is very much a “devil’s in the details” field, because my above explanation didn’t even encapsulate mutual-auth TLS or the underlying machinery of protocol negotiation. (Or the fact that non-forward-secret ciphersuites can be selected.)

AKEs get much more complicated, the more sophisticated your threat model becomes.

For example: Signal’s X3DH and Double Ratchet protocols are components of a very sophisticated AKE. Learn more about them here.

The IETF is working to standardize their own approach, called Messaging Layer Security (MLS), which uses a binary tree of ECDH handshakes to manage state and optimize group operations (called TreeKEM). You can learn more about IETF MLS here.

Password AKEs

Recently, a collection of cryptographers at the IETF’s Crypto Research Forum Group (CFRG) decided to hammer on a series of proposed Password-Authenticated Key Exchange (PAKE) protocols.

PAKEs come in two flavors: Balanced (mutually authenticated) and augmented (one side is a prover, the other is a verifier). Balanced PAKEs are good for encrypted tunnels where you control both endpoints (e.g. WiFi networks), whereas Augmented PAKEs are great for eliminating the risk of password theft in client-server applications, if the server gets hacked.

Ultimately, the CFRG settled on one balanced PAKE (CPace) and one augmented PAKE (OPAQUE).

Consequently, cryptographer Filippo Valsorda managed to implement CPace in 125 lines of Go, using Ristretto255.

I implemented the CPace PAKE yesterday with Go and ristretto255, and it felt like cheating.

📦 https://t.co/Q0kI19JOPY 📦

125 lines of code! Really happy with it and it was a lot of fun.

— Filippo Valsorda (@FiloSottile) March 29, 2020

Why So Complicated?

At the end of the day, an AKE is just a construction that combines key encapsulation with an authentication mechanism.

But how you combine these components together can vary wildly!

Some AKE designs (i.e. Dragonfly, in WPA3) are weaker than others; even if only in the sense of being difficult to implement in constant-time.

The reason there’s so many is that cryptographers tend to collectively decide which algorithms to recommend for standardization.

(n.b. There are a lot more block ciphers than DES, Blowfish, and AES to choose from! But ask a non-cryptographer to name five block ciphers and they’ll probably struggle.)

https://soatok.blog/2020/04/21/authenticated-key-exchanges/

#ake #authenticatedKeyExchange #cryptography #ECDH