Search
Items tagged with: sideChannels
I don’t consider myself exceptional in any regard, but I stumbled upon a few cryptography vulnerabilities in Matrix’s Olm library with so little effort that it was nearly accidental.
It should not be this easy to find these kind of issues in any product people purportedly rely on for private messaging, which many people evangelize incorrectly as a Signal alternative.
Later, I thought I identified an additional vulnerability that would have been much worse, but I was wrong about that one. For the sake of transparency and humility, I’ll also describe that in detail.
This post is organized as follows:
- Disclosure Timeline
- Vulnerabilities in Olm (Technical Details)
- Recommendations
- Background Information
- An Interesting Non-Issue That Looked Critical
I’ve opted to front-load the timeline and vulnerability details to respect the time of busy security professionals.
Please keep in mind that this website is a furry blog, first and foremost, that sometimes happens to cover security and cryptography topics.Many people have, over the years, assumed the opposite and commented accordingly. The ensuing message board threads are usually is a waste of time and energy for everyone involved. So please adjust your expectations.
Art by Harubaki
If you’re curious, you can learn more here.
Disclosure Timeline
- 2024-05-15: I took a quick look at the Matrix source code. I identified two issues and emailed them to their
security@email address.
In my email, I specify that I plan to disclose my findings publicly in 90 days (i.e. on August 14), in adherence with industry best practices for coordinated disclosure, unless they request an extension in writing. - 2024-05-16: I checked something else on a whim and find a third issue, which I also email to their
security@email address. - 2024-05-17: Matrix security team confirms receipt of my reports.
- 2024-05-17: I follow up with a suspected fourth finding–the most critical of them all. They point out that it is not actually an issue, because I overlooked an important detail in how the code is architected. Mea culpa!
- 2024-05-18: A friend discloses a separate finding with Matrix: Media can be decrypted to multiple valid plaintexts using different keys and Malicious homeservers can trick Element/Schildichat into revealing links in E2EE rooms.
They instructed the Matrix developers to consult with me if they needed cryptography guidance. I never heard from them on this externally reported issue. - 2024-07-12: I shared this blog post draft with the Matrix security team while reminding them of the public disclosure date.
- 2024-07-31: Matrix pushes a commit that announces that libolm is deprecated.
- 2024-07-31: I email the Matrix security team asking if they plan to fix the reported issues (and if not, if there’s any other reason I should withhold publication).
- 2024-07-31: Matrix confirms they will not fix these issues (due to its now deprecated status), but ask that I withhold publication until the 14th as originally discussed.
- 2024-08-14: This blog post is publicly disclosed to the Internet.
- 2024-08-14: The lead Matrix dev claims they already knew about these issues, and, in fact, knowingly shipped cryptography code that was vulnerable to side-channel attacks for years. See Addendum.
- 2024-08-23: MITRE has assigned CVE IDs to these three findings.
Vulnerabilities in Olm
I identified the following issues with Olm through a quick skim of their source code on Gitlab:
- AES implementation is vulnerable to cache-timing attacks
- Ed25519 signatures are malleable
- Timing leakage in base64 decoding of private key material
This is sorted by the order in which they were discovered, rather than severity.
AES implementation is vulnerable to cache-timing attacks
a.k.a. CVE-2024-45191
Olm ships a pure-software implementation of AES, rather than leveraging hardware acceleration.
// Substitutes a word using the AES S-Box.WORD SubWord(WORD word){unsigned int result;result = (int)aes_sbox[(word >> 4) & 0x0000000F][word & 0x0000000F];result += (int)aes_sbox[(word >> 12) & 0x0000000F][(word >> 8) & 0x0000000F] << 8;result += (int)aes_sbox[(word >> 20) & 0x0000000F][(word >> 16) & 0x0000000F] << 16;result += (int)aes_sbox[(word >> 28) & 0x0000000F][(word >> 24) & 0x0000000F] << 24;return(result);}
The code in question is called from this code, which is in turn used to actually encrypt messages.
Software implementations of AES that use a look-up table for the SubWord step of the algorithm are famously susceptible to cache-timing attacks.
This kind of vulnerability in software AES was previously used to extract a secret key from OpenSSL and dm-crypt in about 65 milliseconds. Both papers were published in 2005.
A general rule in cryptography is, “attacks only get better; they never get worse“.
As of 2009, you could remotely detect a timing difference of about 15 microseconds over the Internet with under 50,000 samples. Side-channel exploits are generally statistical in nature, so such a sample size is generally not a significant mitigation.
How is this code actually vulnerable?
In the above code snippet, the vulnerability occurs inaes_sbox[/* ... */][/* ... */].
Due to the details of how the AES block cipher works, the input variable (word) is a sensitive value.
Software written this way allows attackers to detect whether or not a specific value was present in one of the processor’s caches.
To state the obvious: Cache hits are faster than cache misses. This creates an observable timing difference.
Such a timing leak allows the attacker to learn the value that was actually stored in said cache. You can directly learn this from other processes on the same hardware, but it’s also observable over the Internet (with some jitter) through the normal operation of vulnerable software.
See also: cryptocoding’s description for table look-ups indexed by secret data.
How to mitigate this cryptographic side-channel
The correct way to solve this problem is to use hardware accelerated AES, which uses distinct processor features to implement the AES round function and side-steps any cache-timing shenanigans with the S-box.
Not only is this more secure, but it’s faster and uses less energy too!
If you’re also targeting devices that don’t have hardware acceleration available, you should first use hardware acceleration where possible, but then fallback to a bitsliced implementation such as the one in Thomas Pornin’s BearSSL.
See also: the BearSSL documentation for constant-time AES.

Ed25519 signatures are malleable
a.k.a. CVE-2024-45193
Ed25519 libraries come in various levels of quality regarding signature validation criteria; much to the chagrin of cryptography engineers everywhere. One of those validation criteria involves signature malleability.
Signature malleability usually isn’t a big deal for most protocols, until suddenly you discover a use case where it is. If it matters, that usually that means you’re doing something with cryptocurrency.
Briefly, if your signatures are malleable, that means you can take an existing valid signature for a given message and public key, and generate a second valid signature for the same message. The utility of this flexibility is limited, and the impact depends a lot on how you’re using signatures and what properties you hope to get out of them.
For ECDSA, this means that for a given signature 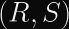
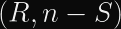
Matrix uses Ed25519, whose malleability is demonstrated between 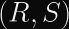
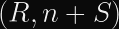
This is trivially possible because S is implicitly reduced modulo the order of the curve, 
0x1000000000000000000000000000000014def9dea2f79cd65812631a5cf5d3ed) and S is encoded as a 256-bit number.
The Ed25519 library used within Olm does not ensure that 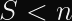
int ed25519_verify(const unsigned char *signature, const unsigned char *message, size_t message_len, const unsigned char *public_key) { unsigned char h[64]; unsigned char checker[32]; sha512_context hash; ge_p3 A; ge_p2 R; if (signature[63] & 224) { return 0; } if (ge_frombytes_negate_vartime(&A, public_key) != 0) { return 0; } sha512_init(&hash); sha512_update(&hash, signature, 32); sha512_update(&hash, public_key, 32); sha512_update(&hash, message, message_len); sha512_final(&hash, h); sc_reduce(h); ge_double_scalarmult_vartime(&R, h, &A, signature + 32); ge_tobytes(checker, &R); if (!consttime_equal(checker, signature)) { return 0; } return 1;}
This is almost certainly a no-impact finding (or low-impact at worst), but still an annoying one to see in 2024.
If you’d like to learn more, this page is a fun demo of Ed25519 malleability.
To mitigate this, I recommend implementing these checks from libsodium.

Timing leakage in base64 decoding of private key material
a.k.a. CVE-2024-45192
If you weren’t already tired of cache-timing attacks based on table look-ups from AES, the Matrix base64 code is also susceptible to the same implementation flaw.
while (pos != end) { unsigned value = DECODE_BASE64[pos[0] & 0x7F]; value <<= 6; value |= DECODE_BASE64[pos[1] & 0x7F]; value <<= 6; value |= DECODE_BASE64[pos[2] & 0x7F]; value <<= 6; value |= DECODE_BASE64[pos[3] & 0x7F]; pos += 4; output[2] = value; value >>= 8; output[1] = value; value >>= 8; output[0] = value; output += 3;}
The base64 decoding function in question is used to load the group session key, which means the attack published in this paper almost certainly applies.
How would you mitigate this leakage?
Steve Thomas (one of the judges of the Password Hashing Competition, among other noteworthy contributions) wrote some open source code a while back that implements base64 encoding routines in constant-time.
The real interesting part is how it avoids a table look-up by using arithmetic (from this file):
// Base64 character set:// [A-Z] [a-z] [0-9] + /// 0x41-0x5a, 0x61-0x7a, 0x30-0x39, 0x2b, 0x2finline int base64Decode6Bits(char src){int ch = (unsigned char) src;int ret = -1;// if (ch > 0x40 && ch < 0x5b) ret += ch - 0x41 + 1; // -64ret += (((0x40 - ch) & (ch - 0x5b)) >> 8) & (ch - 64);// if (ch > 0x60 && ch < 0x7b) ret += ch - 0x61 + 26 + 1; // -70ret += (((0x60 - ch) & (ch - 0x7b)) >> 8) & (ch - 70);// if (ch > 0x2f && ch < 0x3a) ret += ch - 0x30 + 52 + 1; // 5ret += (((0x2f - ch) & (ch - 0x3a)) >> 8) & (ch + 5);// if (ch == 0x2b) ret += 62 + 1;ret += (((0x2a - ch) & (ch - 0x2c)) >> 8) & 63;// if (ch == 0x2f) ret += 63 + 1;ret += (((0x2e - ch) & (ch - 0x30)) >> 8) & 64;return ret;}
Any C library that handles base64 codecs for private key material should use a similar implementation. It’s fine to have a faster base64 implementation for non-secret data.
Worth noting: Libsodium also provides a reasonable Base64 codec.
Recommendations
These issues are not fixed in libolm.
Instead of fixing libolm, the Matrix team recommends all Matrix clients adopt vodozemac.
I can’t speak to the security of vodozemac.

But I can speak against the security of libolm, so moving to vodozemac is probably a good idea. It was audited by Least Authority at one point, so it’s probably fine.
Most Matrix clients that still depended on libolm should treat this blog as public 0day, unless the Matrix security team already notified you about these issues.
Background Information
If you’re curious about the backstory and context of these findings, read on.Otherwise, feel free to skip this section. It’s not pertinent to most audiences. The people that need to read it already know who they are.
End-to-end encryption is one of the topics within cryptography that I find myself often writing about.
In 2020, I wrote a blog post covering end-to-end encryption for application developers. This was published several months after another blog I wrote covering gripes with AES-GCM, which included a shallow analysis of how Signal uses the algorithm for local storage.
In 2021, I published weaknesses in another so-called private messaging app called Threema.
In 2022, after Elon Musk took over Twitter, I joined the Fediverse and sought to build end-to-end encryption support for direct messages into ActivityPub, starting with a specification. Work on this effort was stalled while trying to solve Public Key distribution in a federated environment (which I hope to pick up soon, but I digress).
Earlier this year, the Telegram CEO started fearmongering about Signal with assistance from Elon Musk, so I wrote a blog post urging the furry fandom to move away from Telegram and start using Signal more. As I had demonstrated years prior, I was familiar with Signal’s code and felt it was a good recommendation for security purposes (even if its user experience needs significant work).
I thought that would be a nice, self-contained blog post. Some might listen, most would ignore it, but I could move on with my life.
I was mistaken about that last point.

An overwhelming number of people took it upon themselves to recommend or inquire about Matrix, which prompted me to hastily scribble down my opinion on Matrix so that I might copy/paste a link around and save myself a lot of headache.
Just when I thought the firehose was manageable and I could move onto other topics, one of the Matrix developers responded to my opinion post.
Thus, I decided to briefly look at their source code and see if any major or obvious cryptography issues would fall out of a shallow visual scan.
Since you’re reading this post, you already know how that ended.

Since the first draft of this blog post was penned, I also outlined what I mean when I say an encrypted messaging app is a Signal competitor or not, and published my opinion on XMPP+OMEMO (which people also recommend for private messaging).
Why mention all this?
Because it’s important to know that I have not audited the Olm or Megolm codebases, nor even glanced at their new Rust codebase.
The fact is, I never intended to study Matrix. I was annoyed into looking at it in the first place.
My opinion of their project was already calcified by the previously discovered practically-exploitable cryptographic vulnerabilities in Matrix in 2022.
The bugs described above are the sort of thing I mentally scan for when I first look at a project just to get a feel for the maturity of the codebase. I do this with the expectation (hope, really) of not finding anything at all.
(If you want two specific projects that I’ve subjected to a similar treatment, and failed to discover anything interesting in: Signal and WireGuard. These two set the bar for cryptographic designs.)
It’s absolutely bonkers that an AES cache timing vulnerability was present in their code in 2024.
It’s even worse when you remember that I was inundated with Matrix evangelism in response to recommending furries use Signal.I’m a little outraged because of how irresponsible this is, in context.
It’s so bad that I didn’t even need to clone their git repository, let alone run basic static analysis tools locally.
So if you take nothing else away from this blog post, let it be this:
There is roughly a 0% chance that I got extremely lucky in my mental grep and found the only cryptography implementation flaws in their source code. I barely tried at all and found these issues.
I would bet money on there being more bugs or design flaws that I didn’t find, because this discovery was the result of an extremely half-assed effort to blow off steam.
Wasn’t libolm deprecated in May 2022?
The Matrix developers like to insist that their new Rust hotness “vodozemac” is what people should be using today.
I haven’t looked at vodozemac at all, but let’s pretend, for the sake of argument, that its cryptography is actually secure.
(This is very likely if they turn out to be using RustCrypto for their primitives, but I don’t have the time or energy for that nerd snipe, so I’m not going to look. Least Authority did audit their Rust library, for what it’s worth, and Least Authority isn’t clownshoes.)
It’s been more than 2 years since they released vodozemac. What does the ecosystem penetration for this new library look like, in practice?
A quick survey of the various Matrix clients on GitHub says that libolm is still the most widely used cryptography implementation in the Matrix ecosystem (as of this writing):
| Matrix Client | Cryptography Backend |
|---|---|
| https://github.com/tulir/gomuks | libolm (1, 2) |
| https://github.com/niochat/nio | libolm (1, 2) |
| https://github.com/ulyssa/iamb | vodozemac (1, 2) |
| https://github.com/mirukana/mirage | libolm (1) |
| https://github.com/Pony-House/Client | libolm (1) |
| https://github.com/MTRNord/cetirizine | vodozemac (1) |
| https://github.com/nadams/go-matrixcli | none |
| https://github.com/mustang-im/mustang | libolm (1) |
| https://github.com/marekvospel/libretrix | libolm (1) |
| https://github.com/yusdacra/icy_matrix | none |
| https://github.com/ierho/element | libolm (through the python SDK) |
| https://github.com/mtorials/cordless | none |
| https://github.com/hwipl/nuqql-matrixd | libolm (through the python SDK) |
| https://github.com/maxkratz/element-web | vodozemac (1, 2, 3, 4) |
| https://github.com/asozialesnetzwerk/riot | libolm (wasm file) |
| https://github.com/NotAlexNoyle/Versi | libolm (1, 2) |
3 of the 16 clients surveyed use the new vodozemac library. 10 still use libolm, and 3 don’t appear to implement end-to-end encryption at all.
If we only focus on clients that support E2EE, vodozemac has successfully been adopted by 19% of the open source Matrix clients on GitHub.
I deliberately excluded any repositories that were archived or clearly marked as “old” or “legacy” software, because including those would artificially inflate the representation of libolm. It would make for a more compelling narrative to do so, but I’m not trying to be persuasive here.
Deprecation policies are a beautiful lie. The impact of a vulnerability in Olm or Megolm is still far-reaching, and should be taken seriously by the Matrix community.
Worth calling out: this quick survey, which is based on a GitHub Topic, certainly misses other implementations. Both FluffyChat and Cinny, which were not tagged with this GitHub Topic, depend a language-specific Olm binding.These bindings in turn wrap libolm rather than the Rust replacement, vodozemac.
But the official clients…
I thought the whole point of choosing Matrix over something like Signal is to be federated, and run your own third-party clients?
If we’re going to insist that everyone should be using Element if they want to be secure, that defeats the entire marketing point about third-party clients that Matrix evangelists cite when they decry Signal’s centralization.
So I really don’t want to hear it.
An Interesting Non-Issue That Looked Critical
As I mentioned in the timeline at the top, I thought I found a fourth issue with Matrix’s codebase. Had I been correct, this would have been a critical severity finding that the entire Matrix ecosystem would need to melt down to remediate.
Fortunately for everyone, I made a mistake, and there is no fourth vulnerability after all.
However, I thought it would be interesting to write about what I thought I found, the impact it would have had if it were real, and why I believed it to be an issue.
Let’s start with the code in question:
void ed25519_sign(unsigned char *signature, const unsigned char *message, size_t message_len, const unsigned char *public_key, const unsigned char *private_key) { sha512_context hash; unsigned char hram[64]; unsigned char r[64]; ge_p3 R; sha512_init(&hash); sha512_update(&hash, private_key + 32, 32); sha512_update(&hash, message, message_len); sha512_final(&hash, r); sc_reduce(r); ge_scalarmult_base(&R, r); ge_p3_tobytes(signature, &R); sha512_init(&hash); sha512_update(&hash, signature, 32); sha512_update(&hash, public_key, 32); sha512_update(&hash, message, message_len); sha512_final(&hash, hram); sc_reduce(hram); sc_muladd(signature + 32, hram, private_key, r);}
The highlighted segment is doing pointer arithmetic. This means it’s reading 32 bytes, starting from the 32nd byte in private_key.
What’s actually happening here is: private_key is the SHA512 hash of a 256-bit seed. If you look at the function prototype, you’ll notice that public_key is a separate input.
Virtually every other Ed25519 implementation I’ve ever looked at before expected users to provide a 32 byte seed followed by the public key as a single input.
This led me to believe that this private_key + 32 pointer arithmetic was actually using the public key for calculating r.
The variable r (not to be confused with big R) generated via the first SHA512 is the nonce for a given signature, it must remain secret for Ed25519 to remain secure.
If r is known to an attacker, you can do some arithmetic to recover the secret key from a single signature.
Because I had mistakenly believed that r was calculated from the SHA512 of only public inputs (the public key and message), which I must emphasize isn’t correct, I had falsely concluded that any previously intercepted signature could be used to steal user’s private keys.

But because private_key was actually the full SHA512 hash of the seed, rather than the seed concatenated with the public key, this pointer arithmetic did NOT use the public key for the calculation of r, so this vulnerability does not exist.
If the code did what I thought it did, however, this would have been a complete fucking disaster for the Matrix ecosystem. Any previously intercepted message would have allowed an attacker to recover a user’s secret key and impersonate them. It wouldn’t be enough to fix the code; every key in the ecosystem would need to be revoked and rotated.
Whew!
I’m happy to be wrong about this one, because that outcome is a headache nobody wants.
So no action is needed, right?
Well, maybe.
Matrix’s library was not vulnerable, but I honestly wouldn’t put it past software developers at large to somehow, somewhere, use the public key (rather than a secret value) to calculate the EdDSA signature nonces as described in the previous section.
To that end, I would like to propose a test vector be added to the Wycheproof test suite to catch any EdDSA implementation that misuses the public key in this way.
Then, if someone else screws up their Ed25519 implementation in the exact way I thought Matrix was, the Wycheproof tests will catch it.
For example, here’s a vulnerable test input for Ed25519:
{ "should-fail": true, "secret-key": "d1d0ef849f9ec88b4713878442aeebca5c7a43e18883265f7f864a8eaaa56c1ef3dbb3b71132206b81f0f3782c8df417524463d2daa8a7c458775c9af725b3fd", "public-key": "f3dbb3b71132206b81f0f3782c8df417524463d2daa8a7c458775c9af725b3fd", "message": "Test message", "signature": "ffc39da0ce356efb49eb0c08ed0d48a1cadddf17e34f921a8d2732a33b980f4ae32d6f5937a5ed25e03a998e4c4f5910c931b31416e143965e6ce85b0ea93c09"}
A similar test vector would also be worth creating for Ed448, but the only real users of Ed448 were the authors of the xz backdoor, so I didn’t bother with that.
(None of the Project Wycheproof maintainers knew this suggestion is coming, by the way, because I was respecting the terms of the coordinated disclosure.)
Closing Thoughts
Despite finding cryptography implementation flaws in Matric’s Olm library, my personal opinion on Matrix remains largely unchanged from 2022. I had already assumed it would not meet my bar for security.
Cryptography engineering is difficult because the vulnerabilities you’re usually dealing with are extremely subtle. (Here’s an unrelated example if you’re not convinced of this general observation.) As SwiftOnSecurity once wrote:
https://twitter.com/SwiftOnSecurity/status/832058185049579524
The people that developed Olm and Megolm has not proven themselves ready to build a Signal competitor. In balance, most teams are not qualified to do so.
I really wish the Matrix evangelists would accept this and stop trying to cram Matrix down other people’s throats when they’re talking about problems with other platforms entirely.
More important for the communities of messaging apps:You don’t need to be a Signal competitor. Having E2EE is a good thing on its own merits, and really should be table stakes for any social application in 2024.
It’s only when people try to advertise their apps as a Signal alternative (or try to recommend it instead of Signal), and offer less security, that I take offense.
Just be your own thing.
My work-in-progress proposal to bring end-to-end encryption to the Fediverse doesn’t aim to compete with Signal. It’s just meant to improve privacy, which is a good thing to do on its own merits.
If I never hear Matrix evangelism again after today, it would be far too soon.
If anyone feels like I’m picking on Matrix, don’t worry: I have far worse things to say about Telegram, Threema, XMPP+OMEMO, Tox, and a myriad other projects that are hungry for Signal’s market share but don’t measure up from a cryptographic security perspective.
If Signal fucked up as bad as these projects, my criticism of Signal would be equally harsh. (And remember, I have looked at Signal before.)
Addendum (2024-08-14)
One of the lead Matrix devs posted a comment on Hacker News after this blog post went live that I will duplicate here:
the author literally picked random projects from github tagged as matrix, without considering their prevalence or whether they are actually maintained etc.if you actually look at % of impacted clients, it’s tiny.
meanwhile, it is very unclear that any sidechannel attack on a libolm based client is practical over the network (which is why we didn’t fix this years ago). After all, the limited primitives are commented on in the readme and https://github.com/matrix-org/olm/issues/3 since day 1.
So the Matrix developers already knew about these vulnerabilities, but deliberately didn’t fix them, for years.
Congratulations, you’ve changed my stance. It used to be “I don’t consider Matrix a Signal alternative and they’ve had some embarrassing and impactful crypto bugs but otherwise I don’t care”. Now it’s a stronger stance:
Don’t use Matrix.
I had incorrectly assumed ignorance, when it was in fact negligence.
There’s no reasonable world in which anyone should trust the developers of cryptographic software (i.e., libolm) that deliberately ships with side-channels for years, knowing they’re present, and never bother to fix them.
This is fucking clownshoes.
https://soatok.blog/2024/08/14/security-issues-in-matrixs-olm-library/
#crypto #cryptography #endToEndEncryption #Matrix #sideChannels #vuln
A lot of recent (and upcoming) blog posts I’ve written, and Fediverse discussions I’ve participated in, have been about the security of communication products.My criticism of these products is simply that, from a cryptography and security perspective, they’re not a real competitor to Signal.
For all its other faults, Signal sets the bar for secure private messaging. It’s a solid security tool, even if its user experience and feature set leaves a lot of people disappointed. I highly recommend it over, say, Telegram.
In response to my post about jettisoning Telegram, quite a few people have tried to evangelize other products. For example:
Edit: Oh yeah, DON’T USE SIGNAL. Use Matrix instead, offers the benefits of signal without the drawbacks of lack of sync and phone number requirements and is decentralized. The fact that everyone is going gaga for signal as “the BEST messaging app” should be a big red flag in and of itself, because hype trains like this aren’t organic, just saying.
So, let me explain what it means for a communication product to qualify as a Signal competitor from the perspective of someone whose job involves auditing cryptography implementations.The Minimum Bar to Clear
Open Source
Every private messaging app must be open source in order to qualify as a Signal competitor.If it’s not open source, it’s not even worth talking about.
End-to-End Encryption
Messages MUST be end-to-end encrypted. This means that you encrypt on one participant’s device, decrypt on another’s, and nobody in the middle can observe plaintext.When I say MUST, I mean the RFC 2119 keyword.
There must never be a “transmit plaintext” option. No excuses. Secure cryptography is not interoperable with insecure cryptography. If you allow a “transmit plaintext” mode for any reason whatsoever, you have failed to build an encryption product that meets the bar.
This disqualifies Matrix.
This disqualifies Telegram.
This disqualifies XMPP + OMEMO.
This alone disqualifies a lot of so-called private messaging apps.
This doesn’t mean your product is insecure, or that I’m aware of any specific ways to break it.
It just doesn’t occupy the same mindshare as Signal, which only transmits encrypted data and doesn’t have a plaintext protocol to downgrade to.
Therefore, it’s not a goddamn Signal alternative.
How You Encrypt Matters
Signal normalized the use of AES-256-CBC with HMAC-SHA256.Facebook’s “Secret Conversations” feature deviated from this and preferred AES-GCM for attachments, but this bit them when the Invisible Salamanders attack was discovered.
The way Signal uses AES+HMAC is fine for their use case, but building a secure committing AEAD mode (rather than merely AE) out of these primitives is nontrivial.
If you’re aiming to compete with Signal on security, you should, at minimum, expect to engage with a cryptography auditing firm at least once a year to review and re-review your protocol designs and implementations.
I Will Heavily Scrutinize Your Group Messaging Protocols
Group messaging is one of those topics that might sound easy if you can do peer-to-peer messaging securely, but is catastrophically difficult once you get into the details.See also: My blog post about Threema.
If you want a starting point, look at RFC 9420 (Messaging Layer Security, which is a group key agreement protocol for messaging apps).
How You Manage Keys Matters
Tox attempted to build atop NaCl’s crypto_box interface, but this is not suitable for a general purpose secure messaging due to a lack of KCI Security.Key management (which is the focus of an upcoming blog post) is a problem that almost everyone underestimates. It’s also the most user-facing aspect of these messaging applications.
WhatsApp uses Key Transparency to scale user trust. I’m proposing something similar for E2EE for the Fediverse.
This is a much better strategy than expecting users to manually verify “fingerprints”.
Don’t look at OpenPGP as a role model when it comes to user experience. Johnny still cannot fucking encrypt.
Your Feature Should Not Bypass Privacy
Want to add all sorts of frills, like video chat or some dumb bullshit with AI and/or blockchain to secure the attention of venture capitalist investors?You’d better not implement them in such a way that leaks users’ messages or search queries to your service.
The main reason Signal is “missing” features is because they are thoughtful about how these features are designed and implemented.
Guess what happens if you prioritize shipping features over privacy and cryptography engineering?
That’s right: You stop being a contender for a Signal alternative.
So What?
If your fave isn’t a viable alternative to Signal, don’t fucking recommend it to people in response to me recommending Signal.That’s all I ask.
Art: Scruff
But what about…?
I’m not here to discuss your use cases, or usability, or anything else. I’m also not saying that Signal is perfect!Signal is a private messaging app that I would feel safe recommending whistleblowers to use. It meets all these requirements.
In order to be a Signal competitor, no matter how much you like your app, it needs to meet them too, otherwise it isn’t a Signal competitor. Them’s the rules!
There may be other requirements that are more important to you, that Signal doesn’t meet. That’s fine! You can like other things.
But unless your favorite widget also meets all of the things on this page, it’s not a valid competitor from a security and privacy perspective, and therefore I don’t want to fucking hear about it in response to me saying “use Signal until something better comes along”.
Capiche?
Addendum (2024-08-01)
Since I originally posted this, there have been a lot of opinions expressed and questions asked about messaging apps that have nothing to do with cryptographic security.Those are good discussions to have, elsewhere. Hell, most of this discussion would be a better response to my other blog post than this one.
The goal of this post was to specify what the minimum bar is for a different app to qualify as a Signal competitor. It’s written from the perspective of someone whose career is in applied cryptography.
If you have thoughts, feelings, opinions, questions, or concerns about messaging apps (including but not limited to Signal), that’s wonderful.
But this specific blog post is not the correct place to voice them!
Especially if the first line of your response is “you’re too focused on [technology, security, cryptography] (select appropriate)”.
Because… no shit? That’s the entire point of this particular post. It’s narrowly scoped for a reason. Please respect that.
My upcoming vulnerability disclosure in Matrix will make the same point, but I wanted a separate, less distracting blog post to link people to when someone tries to evangelize another chat app instead of Signal, especially if they make security claims while doing so.
https://soatok.blog/2024/07/31/what-does-it-mean-to-be-a-signal-competitor/
#cryptography #endToEndEncryption #privateMessengers #Signal

Previously on Dead Ends in Cryptanalysis, we talked about length-extension attacks and precisely why modern hash functions like SHA-3 and BLAKE2 aren’t susceptible.
The art and science of side-channel cryptanalysis is one of the subjects I’m deeply fascinated by, and it’s something you’ll hear me yap about a lot on this blog in the future.
Since my background before computer security was in web development, I spend a lot of time talking about timing side-channels in particular, as well as their mitigations (see also: constant-time-js).

(Art by Khia.)
However, timing side-channels aren’t omnipotent. Even if your code isn’t constant-time, that doesn’t mean you necessarily have a vulnerability. Case in point:
Length Leaks Are Usually Nothing-Burgers
If you look closely at a constant-time string equality function, you’ll see some clause that looks like this:
if (left.length !== right.length) return false;
A common concern that crops up in bikeshedding discussions about the correct implementation of a constant-time compare is, “This will fail fast if two strings of non-equal length are provided; doesn’t this leak information about the strings being compared?”
Sure, but it won’t affect the security of the application that uses it. Consider a contrived example:
- You’re encrypting with AES-CTR then authenticating the ciphertext with HMAC-SHA256 (Encrypt then MAC).
- For added fun, let’s assume you’re using HKDF-HMAC-SHA512 with a 256-bit salt to derive separate a separate encryption keys and MAC keys from the input key. This salt is prepended to the ciphertext and included as an input to the HMAC tag calculation. Now you don’t have to worry about cryptographic wear-out.
- You’re padding the plaintext to exactly 16 kilobytes prior to encryption, because the exact length of the plaintext is considered sensitive.
- You remove the padding after decryption.
- Your constant-time comparison is used to validate the HMAC tags.
Even though the length of your plaintext is sensitive, it doesn’t really matter that length mismatches leak here: The inputs to the constant-time compare are always HMAC-SHA256 outputs. They will always be 32 bytes (256 bits) long. This is public knowledge.
If you’ve somehow managed to design a protocol that depends on the secrecy of the length of a non-truncated HMAC-SHA256 output to be secure, you’ve probably fucked up something fierce.
However, if you were comparing the unpadded plaintexts with this function–or passing the unpadded plaintext to a hash function–you might have cause for concern.

(Art by Khia.)
When Do Timing Leaks Cause Impact?
Timing side-channels only lead to a vulnerability when they reveal some information about one of the secret inputs to a cryptographic function.
- Leaking how many leading bytes match when comparing HMACs can allow an attacker to forge a valid authentication tag for a chosen message–which often enables further attacks (e.g. padding oracles with AES-CBC + HMAC). The cryptographic secret is the correct authentication tag for a chosen message under a key known only to the defender.
- Leaking the number of leading zeroes introduced the risk of lattice attacks in TLS when used with Diffie-Hellman ciphersuites. See also: the Raccoon Attack. The cryptographic secret is the zero-trimmed shared secret, which is an input to a hash function.
- Leaking the secret number
in the modular inverse step when calculating an ECDSA signature gives attackers enough information to recover the secret key. This can happen if you’re using non-constant-time arithmetic.
Timing attacks can even break state-of-the-art cryptography projects, like the algorithms submitted to NIST’s Post-Quantum Cryptography standardization effort:
https://twitter.com/EllipticKiwi/status/1295670085969838080
However–and this is important–if what leaks is a public input (n.b. something the attackers already knows anyway), then who cares?

Why Timing Leaks Don’t Break Signature Verification
If you’re reviewing some cryptography library and discovered a timing leak in the elliptic curve signature verification function, you might feel tempted to file a vulnerability report with the maintainers of the library.
If so, you’re wasting your time and theirs, for two reasons:
- Signature verification is performed over public inputs (message, public key, signature).
- Knowing which byte verification the comparison fails on isn’t sufficient for forging a signature for a chosen message.
The first part is obvious (and discussed above), but the second might seem untrue at first: If HMAC breaks this way, why doesn’t ECDSA also suffer here?
The Anatomy of Elliptic Curve Digital Signatures
Elliptic curve signatures are usually encoded as 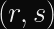
In the case of ECDSA, you calculate two numbers (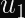
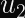
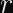
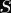
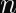
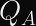
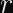
Why Don’t Timing Attacks Do Anything Here?
Even with a timing leak on the string compare function in hand, you cannot easily find a valid 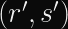
- The derivation of
is effectively an All-Or-Nothing Transform based on secret inputs.
- The curve point equation
) multiplies the ratio r/s by the public key (because
).
In order to calculate a valid 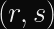
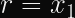
It’s not impossible to calculate this value, but it’s computationally infeasible, and the difficulty of this problem is approximately one fourth the signature size. That is to say, 512-bit signatures, derived from 256-bit keys, have a security level of 128 bits.
Thus, timing leakage won’t let you perform an existential forgery here.

(Art by Khia.)
Under What Conditions Could Timing Side-Channels Matter to ECDSA Verification?
Suppose you have a JSON Web Token library that’s vulnerable to the type confusion attack (wherein you can swap out the "alg":"ES256" with "alg":"HS256" and then use the public key as if it was an HMAC symmetric key).
In this hypothetical scenario, let’s say you’re using this JWT library in an OIDC-like configuration, where the identity provider signs tokens and the application verifies them, using a public key known to the application.
Also assume, for absolutely contrived reasons, that the public key is not known to the attacker.
If you had a timing attack that leaks the public key, that would be a viable (if horrendously slow) way to make the vulnerability exploitable.
However, even in this setup, the timing leak still doesn’t qualify as a real vulnerability. It merely defeats attempts at Security Through Obscurity. The real vulnerability is any JWT library that allows this attack (or alg=none).
Additionally, you can recover the public key if you have sufficient knowledge of the curve algorithm used, message signed, etc.–which you do if the algorithm is ES256–so you don’t really even need a timing leak for this. Consequently, timing leaks would only help you if the original algorithm was something custom and obscure to attackers.
(Aside: there are two possible public keys from each signature, so the signature alone isn’t sufficient for uniquely identifying public keys. If you’re hoping to reduce protocol bandwidth through this trick, it won’t work.)
TL;DR
In order for a timing leak to be useful for cryptanalysis, it cannot leak a publicly-known input to the cryptographic operation.
https://soatok.blog/2021/06/07/dead-ends-in-cryptanalysis-2-timing-side-channels/
#cryptanalysis #crypto #cryptography #deadEndsInCryptanalysis #ECDSA #sideChannels #Technology #timingAttacks
This is the first entry in a (potentially infinite) series of dead end roads in the field of cryptanalysis.Cryptography engineering is one of many specialties within the wider field of security engineering. Security engineering is a discipline that chiefly concerns itself with studying how systems fail in order to build better systems–ones that are resilient to malicious acts or even natural disasters. It sounds much simpler than it is.
If you want to develop and securely implement a cryptography feature in the application you’re developing, it isn’t enough to learn how to implement textbook descriptions of cryptography primitives during your C.S. undergrad studies (or equivalent). An active interest in studying how cryptosystems fail is the prerequisite for being a cryptography engineer.
Thus, cryptography engineering and cryptanalysis research go hand-in-hand.
Pictured: How I feel when someone tells me about a novel cryptanalysis technique relevant to the algorithm or protocol I’m implementing. (Art by Khia.)
If you are interested in exploring the field of cryptanalysis–be it to contribute on the attack side of cryptography or to learn better defense mechanisms–you will undoubtedly encounter roads that seem enticing and not well-tread, and it might not be immediately obvious why the road is a dead end. Furthermore, beyond a few comparison tables on Wikipedia or obscure Stack Exchange questions, the cryptology literature is often sparse on details about why these avenues lead nowhere.
So let’s explore where some of these dead-end roads lead, and why they stop where they do.
(Art by Kyume.)
Length Extension Attacks
It’s difficult to provide a better summary of length extension attacks than what Skull Security wrote in 2012. However, that only addresses “What are they?”, “How do you use them?”, and “Which algorithms and constructions are vulnerable?”, but leaves out a more interesting question: “Why were they even possible to begin with?”An Extensive Tale
Tale, not tail! (Art by Swizz.)
To really understand length extension attacks, you have to understand how cryptographic hash functions used to be designed. This might sound intimidating, but we don’t need to delve too deep into the internals.
A cryptographic hash function is a keyless pseudorandom transformation from a variable length input to a fixed-length output. Hash functions are typically used as building blocks for larger constructions (both reasonable ones like HMAC-SHA-256, and unreasonable ones like my hash-crypt project).
However, hash functions like SHA-256 are designed to operate on sequential blocks of input. This is because sometimes you need to stream data into a hash function rather than load it all into memory at once. (This is why you can sha256sum a file larger than your available RAM without crashing your computer or causing performance headaches.)
A streaming hash function API might look like this:
class MyCoolHash(BaseHashClass): @staticmethod def init(): """ Initialize the hash state. """ def update(data): """ Update the hash state with additional data. """ def digest(): """ Finalize the hash function. """ def compress(): """ (Private method.) """
To use it, you’d callhash = MyCoolHash.init()and then chain togetherhash.update()calls with data as you load it from disk or the network, until you’ve run out of data. Then you’d calldigest()and obtain the hash of the entire message.There are two things to take away right now:
- You can call
update()multiple times, and that’s valid.- Your data might not be an even multiple of the internal block size of the hash function. (More often than not, it won’t be!)
So what happens when you call
digest()and the amount of data you’ve passed toupdate()is not an even multiple of the hash size?For most hash functions, the answer is simple: Append some ISO/IEC 7816-4 padding until you get a full block, run that through a final iteration of the internal compression function–the same one that gets called on
update()–and then output the current internal state.Let’s take a slightly deeper look at what a typical runtime would look like for the MyCoolHash class I sketched above:
hash = MyCoolHash.init()
- Initialize some variables to some constants (initialization vectors).
hash.update(blockOfData)
- Start with any buffered data (currently none), count up to 32 bytes. If you’ve reached this amount, invoke
compress()on that data and clear the buffer. Otherwise, just append blockOfData to the currently buffered data.- For every 32 byte of data not yet touched by
compress(), invokecompress()on this block (updating the internal state).- If you have any leftover bytes, append to the internal buffer for the next invocation to process.
hash.update(moreData)
- Same as before, except there might be some buffered data from step 2.
output = hash.digest()
- If you have any data left in the buffer, append a 0x80 byte followed by a bunch of 0x00 bytes of padding until you reach the block size. If you don’t, you have an entire block of padding (0x80 followed by 0x00s).
- Call
compress()one last time.- Serialize the internal hash state as a byte array or hexadecimal-encoded string (depending on usage). Return that to the caller.
This is fairly general description that will hold for most older hash functions. Some details might be slightly wrong (subtly different padding scheme, whether or not to include a block of empty padding on
digest()invocations, etc.).The details aren’t super important. Just the rhythm of the design.
init()update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
- …
digest()
- load buffer, pad,
compress()- serialize internal state
- return
And thus, without having to know any of the details about what
compress()even looks like, the reason why length extension attacks were ever possible should leap out at you!
Art by Khia.
If it doesn’t, look closely at the difference between
update()anddigest().There are only two differences:
update()doesn’t pad before callingcompress()digest()returns the internal state thatcompress()always mutatesThe reason length-extension attacks are possible is that, for some hash functions, the output of
digest()is its full internal state.This means that you can run take an existing hash function and pretend it’s the internal state after an
update()call instead of adigest()call by appending the padding and then, after callingcompress(), appending additional data of your choice.The (F)Utility of Length Extension
Length-Extension Attacks are mostly used for attacking naive message authentication systems where someone attempts to authenticate a message (M) with a secret key (k), but they construct it like so:
auth_code = vulnerable_hash(k.append(M))
If this sounds like a very narrow use-case, that’s because it is. However, it still broke Flickr’s API once, and it’s a popular challenge for CTF competitions around the world.Consequently, length-extension attacks are sometimes thought to be vulnerabilities of the construction rather than a vulnerability of the hash function. For a Message Authentication Code construction, these are classified under canonicalization attacks.
After all, even though SHA-256 is vulnerable to length-extension, but you can’t actually exploit it unless someone is using it in a vulnerable fashion.
That being said, it’s often common to say that hash functions like SHA-256 and SHA-512 are prone to length-extension.
Ways to Avoid Length-Extension Attacks
Use HMAC. HMAC was designed to prevent these kinds of attacks.Alternatively, if you don’t have any cryptographic secrets, you can always do what bitcoin did: Hash your hash again.
return sha256(sha256(message))
Note: Don’t actually do that, it’s dangerous for other reasons. You also don’t want to take this to an extreme. If you iterate your hash too many times, you’ll reinvent PBKDF1 and its insecurity. Two is plenty.Or you can do something really trivial (which ultimately became another standard option in the SHA-2 family of hash functions):
Always start with a 512-bit hash and then truncate your output so the attacker never recovers the entire internal state of your hash in order to extend it.
That’s why you’ll sometimes see SHA-512/224 and SHA-512/256 in a list of recommendations. This isn’t saying “use one or the other”, that’s the (rather confusing) notation for a standardized SHA-512 truncation.
Note: This is actually what SHA-384 has done all along, and that’s one of the reasons why you see SHA-384 used more than SHA-512.
If you want to be extra fancy, you can also just use a different hash function that isn’t vulnerable to length extension, such as SHA-3 or BLAKE2.
Questions and Answers
Art by Khia.
Why isn’t BLAKE2 vulnerable to length extension attacks?
Quite simply: It sets a flag in the internal hash state before compressing the final buffer.If you try to deserialize this state then invoke
update(), you’ll get a different result than BLAKE2’scompress()produced duringdigest().For a secure hash function, a single bit of difference in the internal state should result in a wildly different output. (This is called the avalanche effect.)
Why isn’t SHA-3 vulnerable to length extension attacks?
SHA-3 is a sponge construction whose internal state is much larger than the hash function output. This prevents an attacker from recovering the hash function’s internal state from a message digest (similar to the truncated hash function discussed above).Why don’t length-extension attacks break digital signature algorithms?
Digital signature algorithms–such as RSASSA, ECDSA, and EdDSA–take a cryptographic hash of a message and then perform some asymmetric cryptographic transformation of the hash with the secret key to produce a signature that can be verified with a public key. (The exact details are particular to the signature algorithm in question.)Length-extension attacks only allow you to take a valid H(k || m) and produce a valid H(k || m || padding || extra) hash that will validate, even if you don’t know k. They don’t magically create collisions out of thin air.
Even if you use a weak hash function like SHA-1, knowing M and H(M) is not sufficient to calculate a valid signature. (You need to be able to know these values in order to verify the signature anyway.)
The security of digital signature algorithms depends entirely on the secrecy of the signing key and the security of the asymmetric cryptographic transformation used to generate a signature. (And its resilience to side-channel attacks.)
However, a more interesting class of attack is possible for systems that expect digital signatures to have similar properties as cryptographic hash functions. This would qualify as a protocol vulnerability, not a length-extension vulnerability.
TL;DR
Art by Khia.
Length-extension attacks exploit a neat property of a few cryptographic hash functions–most of which you shouldn’t be using in 2020 anyway (SHA-2 is still fine)–but can only be exploited by a narrow set of circumstances.
If you find yourself trying to use length-extension to break anything else, you’ve probably run into a cryptographic dead end and need to backtrack onto more interesting avenues of exploitation–of which there are assuredly many (unless your cryptography is boring).
Next: Timing Side-Channels
https://soatok.blog/2020/10/06/dead-ends-in-cryptanalysis-1-length-extension-attacks/
#cryptanalysis #crypto #cryptographicHashFunction #cryptography #lengthExtensionAttacks

If you’re ever tasked with implementing a cryptography feature–whether a high-level protocol or a low-level primitive–you will have to take special care to ensure you’re not leaking secret information through side-channels.
The descriptions of algorithms you learn in a classroom or textbook are not sufficient for real-world use. (Yes, that means your toy RSA implementation based on GMP from your computer science 101 class isn’t production-ready. Don’t deploy it.)
But what are these elusive side-channels exactly, and how do you prevent them? And in cases where you cannot prevent them, how can you mitigate the risk to your users?

Contents
- Cryptographic Side-Channels
- Side-Channel Prevention and Mitigation
- Design Patterns for Algorithmic Constant-Time Code
- Constant-Time String Comparison
- Alternative: “Double HMAC” String Comparison
- Constant-Time Conditional Select
- Constant-Time String Inequality Comparison
- Constant-Time Integer Multiplication
- Constant-Time Integer Division
- Constant-Time Modular Inversion
- Constant-Time Null-Byte Trimming
- Further Reading and Online Resources
- Errata
Cryptographic Side-Channels
The concept of a side-channel isn’t inherently cryptographic, as Taylor Hornby demonstrates, but a side-channel can be a game over vulnerability in a system meant to maintain confidentiality (even if only for its cryptography keys).
Cryptographic side-channels allow an attacker to learn secret data from your cryptography system. To accomplish this, the attacker doesn’t necessarily study the system’s output (i.e. ciphertext); instead, they observe some other measurement, such as how much time or power was spent performing an operation, or what kind of electromagnetic radiation was emitted.
Important: While being resistant to side-channels is a prerequisite for implementations to be secure, it isn’t in and of itself sufficient for security. The underlying design of the primitives, constructions, and high-level protocols needs to be secure first, and that requires a clear and specific threat model for what you’re building.
Constant-time ECDSA doesn’t help you if you reuse k-values like it’s going out of style, but variable-time ECDSA still leaks your secret key to anyone who cares to probe your response times. Secure cryptography is very demanding.

Timing Leaks
Timing side-channels leak secrets through how much time it takes for an operation to complete.
There are many different flavors of timing leakage, including:
- Fast-failing comparison functions (memcmp() in C)
- Cache-timing vulnerabilities (e.g. software AES)
- Memory access patterns
- Conditional branches controlled by secrets
The bad news about timing leaks is that they’re almost always visible to an attacker over the network (including over the Internet (PDF)).
The good news is that most of them can be prevented or mitigated in software.

Power Usage
Different algorithms or processor operations may require different amounts of power.
For example, squaring a large number may take less power than multiplying two different large numbers. This observation has led to the development of power analysis attacks against RSA.
Power analysis is especially relevant for embedded systems and smart cards, which are easier to extract a meaningful signal from than your desktop computer.
Some information leakage through power usage can be prevented through careful engineering (for example: BearSSL, which uses Montgomery multiplication instead of square-and-multiply).
But that’s not always an option, so generally these risks are mitigated.

Electromagnetic Emissions
Your computer is a reliable source of electromagnetic emissions (such as radio waves). Some of these emissions may reveal information about your cryptographic secrets, especially to an attacker with physical proximity to your device.
The good news is that research into EM emission side-channels isn’t as mature as side-channels through timing leaks or power usage. The bad news is that mitigations for breakthroughs will generally require hardware (e.g. electromagnetic shielding).
![[Glitching] [Glitching]](https://fika.grin.hu/photo/link/10390)
Side-Channel Prevention and Mitigation
Now that we’ve established a rough sense of some of the types of side-channels that are possible, we can begin to identify what causes them and aspire to prevent the leaks from happening–and where we can’t, to mitigate the risk to a reasonable level.
Note: To be clear, I didn’t cover all of the types of side-channels.
Prevention vs. Mitigation
Preventing a side-channel means eliminating the conditions that allow the information leak to occur in the first place. For timing leaks, this means making all algorithms constant-time.
There are entire classes of side-channel leaks that aren’t possible or practical to mitigate in software. When you encounter one, the best you can hope to do is mitigate the risk.
Ideally, you want to make the attack more expensive to pull off than the reward an attacker will gain from it.
What is Constant-Time?
https://www.youtube.com/watch?v=ZD_H1ePLylA
When an implementation is said to be constant-time, what we mean is that the execution time of the code is not a function of its secret inputs.
Vulnerable AES uses table look-ups to implement the S-Box. Constant-time AES is either implemented in hardware, or is bitsliced.
Malicious Environments and Algorithmic Constant-Time
One of the greatest challenges with writing constant-time code is distinguishing between algorithmic constant-time and provably constant-time. The main difference between the two is that you cannot trust your compiler (especially a JIT compiler), which may attempt to optimize your code in a way that reintroduces the side-channel you aspired to remove.
A sufficiently advanced compiler optimization is indistinguishable from an adversary.John Regehr, possibly with apologies to Arthur C. Clarke
For compiled languages, this is a tractable but expensive problem to solve: You simply have to formally verify everything from the source code to the compiler to the silicon chips that the code will be deployed on, and then audit your supply chain to prevent malicious tampering from going undetected.
For interpreted languages (e.g. PHP and JavaScript), this formal verification strategy isn’t really an option, unless you want to formally verify the runtime that interprets scripts and prove that the operations remain constant-time on top of all the other layers of distrust.
Is this level of paranoia really worth the effort?

For that reason, we’re going to assume that algorithmic constant-time is adequate for the duration of this blog post.
If your threat model prevents you from accepting this assumption, feel free to put in the extra effort yourself and tell me how it goes. After all, as a furry who writes blog posts in my spare time for fun, I don’t exactly have the budget for massive research projects in formal verification.
Mitigation with Blinding Techniques
The best mitigation for some side-channels is called blinding: Obfuscating the inputs with some random data, then deobfuscating the outputs with the same random data, such that your keys are not revealed.
Two well-known examples include RSA decryption and Elliptic Curve Diffie-Hellman. I’ll focus on the latter, since it’s not as widely covered in the literature (although several cryptographers I’ve talked with were somehow knowledgeable about it; I suspect gatekeeping is involved).
Blinded ECDH Key Exchange
In typical ECDH implementations, you will convert a point on a Weierstrass curve 
The exact conversion formula is (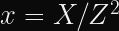
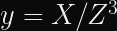
Where does 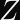

It turns out, the choice for 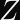
Choosing a random number means the calculations performed over Jacobian coordinates will be obscured by a randomly chosen factor 

I think it’s really cool how one small tweak to the runtime of an algorithm can make it significantly harder to attack.
Design Patterns for Algorithmic Constant-Time Code
Mitigation techniques are cool, but preventing side-channels is a better value-add for most software.
To that end, let’s look at some design patterns for constant-time software. Some of these are relatively common; others, not so much.

If you prefer TypeScript / JavaScirpt, check out Soatok’s constant-time-js library on Github / NPM.
Constant-Time String Comparison
Rather than using string comparison (== in most programming languages, memcmp() in C), you want to compare cryptographic secrets and/or calculated integrity checks with a secure compare algorithm, which looks like this:
- Initialize a variable (let’s call it D) to zero.
- For each byte of the two strings:
- Calculate (lefti XOR righti)
- Bitwise OR the current value of D with the result of the XOR, store the output in D
- When the loop has concluded, D will be equal to 0 if and only if the two strings are equal.
In code form, it looks like this:
<?phpfunction ct_compare(string $left, string $right): bool{ $d = 0; $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { return false; // Lengths differ } for ($i = 0; $i < $length; ++$i) { $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $d |= ($leftCharCode ^ $rightCharCode); } return $d === 0;}
In this example, I’m using PHP’s unpack() function to avoid cache-timing leaks with ord() and chr(). Of course, you can simply use hash_equals() instead of writing it yourself (PHP 5.6.0+).
Alternative: “Double HMAC” String Comparison
If the previous algorithm won’t work (i.e. because you’re concerned your JIT compiler will optimize it away), there is a popular alternative to consider. It’s called “Double HMAC” because it was traditionally used with Encrypt-Then-HMAC schemes.
The algorithm looks like this:
- Generate a random 256-bit key, K. (This can be cached between invocations, but it should be unpredictable.)
- Calculate HMAC-SHA256(K, left).
- Calculate HMAC-SHA256(K, right).
- Return true if the outputs of step 2 and 3 are equal.
This is provably secure, so long as HMAC-SHA256 is a secure pseudo-random function and the key K is unknown to the attacker.
In code form, the Double HMAC compare function looks like this:
<?phpfunction hmac_compare(string $left, string $right): bool{ static $k = null; if (!$k) $k = random_bytes(32); return ( hash_hmac('sha256', $left, $k) === hash_hmac('sha256', $right, $k) );}
Constant-Time Conditional Select
I like to imagine a conversation between a cryptography engineer and a Zen Buddhist, that unfolds like so:
- CE: “I want to eliminate branching side-channels from my code.”
- ZB: “Then do not have branches in your code.”
And that is precisely what we intend to do with a constant-time conditional select: Eliminate branches by conditionally returning between one of two strings, without an IF statement.

This isn’t as tricky as it sounds. We’re going to use XOR and two’s complement to achieve this.
The algorithm looks like this:
- Convert the selection bit (TRUE/FALSE) into a mask value (-1 for TRUE, 0 for FALSE). Bitwise, -1 looks like 111111111…1111111111, while 0 looks like 00000000…00000000.
- Copy the right string into a buffer, call it tmp.
- Calculate left XOR right, call it x.
- Return (tmp XOR (x AND mask)).
Once again, in code this algorithm looks like this:
<?phpfunction ct_select( bool $returnLeft, string $left, string $right): string { $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } // Mask byte $mask = (-$returnLeft) & 0xff; // X $x = (string) ($left ^ $right); // Output = Right XOR (X AND Mask) $output = ''; for ($i = 0; $i < $length; $i++) { $rightCharCode = unpack('C', $right[$i])[1]; $xCharCode = unpack('C', $x[$i])[1]; $output .= pack( 'C', $rightCharCode ^ ($xCharCode & $mask) ); } return $output;}
You can test this code for yourself here. The function was designed to read intuitively like a ternary operator.
A Word of Caution on Cleverness
In some languages, it may seem tempting to use the bitwise trickery to swap out pointers instead of returning a new buffer. But do not fall for this Siren song.
If, instead of returning a new buffer, you just swap pointers, what you’ll end up doing is creating a timing leak through your memory access patterns. This can culminate in a timing vulnerability, but even if your data is too big to fit in a processor’s cache line (I dunno, Post-Quantum RSA keys?), there’s another risk to consider.
Virtual memory addresses are just beautiful lies. Where your data lives on the actual hardware memory is entirely up to the kernel. You can have two blobs with contiguous virtual memory addresses that live on separate memory pages, or even separate RAM chips (if you have multiple).
If you’re swapping pointers around, and they point to two different pieces of hardware, and one is slightly faster to read from than the other, you can introduce yet another timing attack through which pointer is being referenced by the processor.

If you’re swapping between X and Y before performing a calculation, where:
- X lives on RAM chip 1, which takes 3 ns to read
- Y lives on RAM chip 2, which takes 4 ns to read
…then the subsequent use of the swapped pointers reveals whether you’re operating on X or Y in the timing: It will take slightly longer to read from Y than from X.
The best way to mitigate this problem is to never design your software to have it in the first place. Don’t be clever on this one.
Constant-Time String Inequality Comparison
Sometimes you don’t just need to know if two strings are equal, you also need to know which one is larger than the other.
To accomplish this in constant-time, we need to maintain two state variables:
- gt (initialized to 0, will be set to 1 at some point if left > right)
- eq (initialized to 1, will be set to 0 at some point if left != right)
Endian-ness will dictate the direction our algorithm goes, but we’re going to perform two operations in each cycle:
- gt should be bitwise ORed with (eq AND ((right – left) right shifted 8 times)
- eq should be bitwise ANDed with ((right XOR left) – 1) right shifted 8 times
If right and left are ever different, eq will be set to 0.
If the first time they’re different the value for lefti is greater than the value for righti, then the subtraction will produce a negative number. Right shifting a negative number 8 places then bitwise ANDing the result with eq (which is only 1 until two bytes differ, and then 0 henceforth if they do) will result in a value for 1 with gt. Thus, if (righti – lefti) is negative, gt will be set to 1. Otherwise, it remains 0.
At the end of this loop, return (gt + gt + eq) – 1. This will result in the following possible values:
- left < right: -1
- left == right: 0
- left > right: 1
The arithmetic based on the possible values of gt and eq should be straightforward.
- Different (eq == 0) but not greater (gt == 0) means left < right, -1.
- Different (eq == 0) and greater (gt == 1) means left > right, 1.
- If eq == 1, no bytes ever differed, so left == right, 0.
A little endian implementation is as follows:
<?phpfunction str_compare(string $left, string $right): int{ $length = mb_strlen($left, '8bit'); if (mb_strlen($right, '8bit') !== $length) { throw new Exception('ct_select() expects two strings of equal length'); } $gt = 0; $eq = 1; $i = $length; while ($i > 0) { --$i; $leftCharCode = unpack('C', $left[$i])[1]; $rightCharCode = unpack('C', $right[$i])[1]; $gt |= (($rightCharCode - $leftCharCode) >> 8) & $eq; $eq &= (($rightCharCode ^ $leftCharCode) -1) >> 8; } return ($gt + $gt + $eq) - 1;}
Demo for this function is available here.
Constant-Time Integer Multiplication
Multiplying two integers is one of those arithmetic operations that should be constant-time. But on many older processors, it isn’t.

Fortunately, there is a workaround. It involves an algorithm called Ancient Egyptian Multiplication in some places or Peasant Multiplication in others.
Multiplying two numbers 
- Determine the number of operations you need to perform. Generally, this is either known ahead of time or
.
- Set
to 0.
- Until the operation count reaches zero:
- If the lowest bit of
is set, add
to
.
- Left shift
by 1.
- Right shfit
by 1.
- If the lowest bit of
- Return
.
The main caveat here is that you want to use bitwise operators in step 3.1 to remove the conditional branch.
Rather than bundle example code in our blog post, please refer to the implementation in sodium_compat (a pure PHP polyfill for libsodium).
For big number libraries, implementing Karatsuba on top of this integer multiplying function should be faster than attempting to multiply bignums this way.
Constant-Time Integer Division
Although some cryptography algorithms call for integer division, division isn’t usually expected to be constant-time.
However, if you look up a division algorithm for unsigned integers with a remainder, you’ll likely encounter this algorithm, which is almost constant-time:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator if R ≥ D then R := R − D Q(i) := 1 endend
If we use the tricks we learned from implementing constant-time string inequality with constant-time conditional selection, we can implement this algorithm without timing leaks.
Our constant-time version of this algorithm looks like this:
if D = 0 then error(DivisionByZeroException) endQ := 0 -- Initialize quotient and remainder to zeroR := 0 for i := n − 1 .. 0 do -- Where n is number of bits in N R := R << 1 -- Left-shift R by 1 bit R(0) := N(i) -- Set the least-significant bit of R equal to bit i of the numerator compared := ct_compare(R, D) -- Use constant-time inequality -- if R > D then compared == 1, swap = 1 -- if R == D then compared == 0, swap = 1 -- if R < D then compared == -1, swap = 0 swap := (1 - ((compared >> 31) & 1)) -- R' = R - D -- Q' = Q, Q = 1 Rprime := R - D Qprime := Q Qprime(i) := 1 -- The i'th bit is set to 1 -- Replace (R with R', Q with Q') if swap == 1 R = ct_select(swap, Rprime, R) Q = ct_select(swap, Qprime, Q)end
It’s approximately twice as slow as the original, but it’s constant-time.

Constant-Time Modular Inversion
Modular inversion is the calculation of 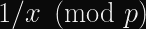
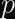
Daniel J. Bernstein and Bo-Yin Yang published a paper on fast constant-time GCD and Modular Inversion in 2019. The algorithm in question is somewhat straightforward to implement (although determining whether or not that implementation is safe is left as an exercise to the rest of us).
A simpler technique is to use Fermat’s Little Theorem: 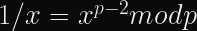
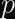
BearSSL provides an implementation (and accompanying documentation) for a constant-time modular inversion algorithm based on Binary GCD.
(In the future, I may update this section of this blog post with an implementation in PHP, using the GMP extension.)
Constant-Time Null-Byte Trimming
Shortly after this guide first went online, security researchers published the Raccoon Attack, which used a timing leak in the number of leading 0 bytes in the pre-master secret–combined with a lattice attack to solve the hidden number problem–to break TLS-DH(E).
To solve this, you need two components:
- A function that returns a slice of an array without timing leaks.
- A function that counts the number of significant bytes (i.e. ignores leading zero bytes, counts from the first non-zero byte).
A timing-safe array resize function needs to do two things:
- Touch every byte of the input array once.
- Touch every byte of the output array at least once, linearly. The constant-time division algorithm is useful here (to calculate x mod n for the output array index).
- Conditionally select between input[x] and the existing output[x_mod_n], based on whether x >= target size.
I’ve implemented this in my constant-time-js library:
Further Reading and Online Resources
If you’re at all interested in cryptographic side-channels, your hunger for knowledge probably won’t be sated by a single blog post. Here’s a collection of articles, papers, books, etc. worth reading.
- BearSSL’s Documentation on Constant-Time Code — A must-read for anyone interested in this topic
- Cryptographically Secure PHP Development — How to write secure cryptography in languages that cryptographers largely neglect
- CryptoCoding — A style guide for writing secure cryptography code in C (with example code!)
- CryptoGotchas — An overview of the common mistakes one can make when writing cryptography code (which is a much wider scope than side-channels)
- Meltdown and Spectre — Two vulnerabilities that placed side-channels in the scope of most of infosec that isn’t interested in cryptography
- Serious Cryptography — For anyone who lacks the background knowledge to fully understand what I’m talking about on this page
Errata
- 2020-08-27: The original version of this blog post incorrectly attributed Jacobian coordinate blinding to ECDSA hardening, rather than ECDH hardening. This error was brought to my attention by Thai Duong. Thanks Thai!
- 2020-08-27: Erin correctly pointed out that omitting memory access timing was a disservice to developers, who might not be aware of the risks involved. I’ve updated the post to call this risk out specifically (especially in the conditional select code, which some developers might try to implement with pointer swapping without knowing the risks involved). Thanks Erin!
I hope you find this guide to side-channels helpful.

Follow my blog for more Defense Against the Bark Arts posts in the future.
https://soatok.blog/2020/08/27/soatoks-guide-to-side-channel-attacks/
#asymmetricCryptography #constantTime #cryptography #ECDH #ECDSA #ellipticCurveCryptography #RSA #SecurityGuidance #sideChannels #symmetricCryptography
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Art by Khia.
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting
(at 50% probability) blocks.
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
you expect from AES.
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.This is because Grover’s quantum search algorithm can search
unsorted items in
time, which can be used to reduce the total number of possible secrets from
to
. This effectively cuts the security level, expressed in bits, in half.
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
(plaintext, key) pairs that produce any given ciphertext block.
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
times as many AES-256 keys as there are possible plaintext/ciphertexts. Keep this in mind for AES-GCM.
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
This is unacceptable!
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
: A number that must only be used once).
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
The deeper you look into AES-GCM’s design, the harder you will feel this sticker.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called. This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
This is often sold as an advantage: Reusingallows for better performance. However, it makes GCM brittle: Reusing a nonce allows an attacker to recover H and then forge messages forever. This is called the “forbidden attack”, and led to real world practical breaks.
Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.If we assume AES is well-behaved, we can deduce that there are approximately
different 256-bit keys that will map a single plaintext block to a single ciphertext block.
This is trivial to calculate. Simply divide the number of possible keys (
) by the number of possible block states (
) to yield the number of keys that produce a given ciphertext for a single block of plaintext:
.
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
.
This means there are approximately
independent keys that will map a given all-zero plaintext block to an arbitrarily chosen value of
(if we assume AES doesn’t have weird biases).
Credit: Harubaki
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection ofas a 128-bit pseudorandom function, rather than a 128-bit permutation. As a result, you an expect a collision with 50% probability after only
different keys are selected.
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a
collision risk. So that means our safety limit is actually
different AES keys before you have to worry about
reuse.
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of
different AES keys, you have to either accept the risk or stop using AES-GCM.
If you have a billion users (
), the safety limit is breached after
AES keys per user (approximately 262,000).
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.is used for block multiplication, and
(the value of
with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.
The arrow highlighted with green is HF.
It’s tempting to think that a reuse of
isn’t a concern because
will necessarily be randomized, which prevents an attacker from observing when
collides. It’s certainly true that the single-block collision risk discussed previously for
will almost certainly not also result in a collision for
. And since
isn’t reused unless a nonce is reused (which also leaks
directly), this might seem like a non-issue.
Art by Khia.
However, it’s straightforward to go from a condition of
reuse to an adaptive chosen-ciphertext attack.
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- Use your knowledge of
, the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of
for a given nonce.
- Calculate a new authentication tag for a chosen ciphertext using
and your candidate
value, then replay it into the target system.
While the blinding offered by XORing the final output with
is sufficient to stop
from being leaked directly, the protection is one-way.
Ergo, a collision in
is not sufficiently thwarted by
.
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
is
, and finding an untargeted collision requires being able to observe more than
different sessions, and somehow distinguish when
collides.
As a user, you know that after
different keys, you’ve crossed the safety boundary for avoiding
collisions. But as an attacker, you need
bites at the apple, not
. Additionally, you need some sort of oracle or distinguisher for when this happens.
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
is challenging to work with. You would need the computational and data storages of a major cloud service provider to even think about pulling the attack off.
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
bytes long, under a given (key, nonce) pair.
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
messages.
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atrandom nonces, which represents a collision probability of one in 4 billion.
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
I’m glad you asked!
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
messages (for the same collision probability as AES-GCM).
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography










