Previously on Dead Ends in Cryptanalysis, we talked about length-extension attacks and precisely why modern hash functions like SHA-3 and BLAKE2 aren’t susceptible.
The art and science of side-channel cryptanalysis is one of the subjects I’m deeply fascinated by, and it’s something you’ll hear me yap about a lot on this blog in the future.
Since my background before computer security was in web development, I spend a lot of time talking about timing side-channels in particular, as well as their mitigations (see also: constant-time-js).

(Art by Khia.)
However, timing side-channels aren’t omnipotent. Even if your code isn’t constant-time, that doesn’t mean you necessarily have a vulnerability. Case in point:
Length Leaks Are Usually Nothing-Burgers
If you look closely at a constant-time string equality function, you’ll see some clause that looks like this:
if (left.length !== right.length) return false;
A common concern that crops up in bikeshedding discussions about the correct implementation of a constant-time compare is, “This will fail fast if two strings of non-equal length are provided; doesn’t this leak information about the strings being compared?”
Sure, but it won’t affect the security of the application that uses it. Consider a contrived example:
- You’re encrypting with AES-CTR then authenticating the ciphertext with HMAC-SHA256 (Encrypt then MAC).
- For added fun, let’s assume you’re using HKDF-HMAC-SHA512 with a 256-bit salt to derive separate a separate encryption keys and MAC keys from the input key. This salt is prepended to the ciphertext and included as an input to the HMAC tag calculation. Now you don’t have to worry about cryptographic wear-out.
- You’re padding the plaintext to exactly 16 kilobytes prior to encryption, because the exact length of the plaintext is considered sensitive.
- You remove the padding after decryption.
- Your constant-time comparison is used to validate the HMAC tags.
Even though the length of your plaintext is sensitive, it doesn’t really matter that length mismatches leak here: The inputs to the constant-time compare are always HMAC-SHA256 outputs. They will always be 32 bytes (256 bits) long. This is public knowledge.
If you’ve somehow managed to design a protocol that depends on the secrecy of the length of a non-truncated HMAC-SHA256 output to be secure, you’ve probably fucked up something fierce.
However, if you were comparing the unpadded plaintexts with this function–or passing the unpadded plaintext to a hash function–you might have cause for concern.

(Art by Khia.)
When Do Timing Leaks Cause Impact?
Timing side-channels only lead to a vulnerability when they reveal some information about one of the secret inputs to a cryptographic function.
- Leaking how many leading bytes match when comparing HMACs can allow an attacker to forge a valid authentication tag for a chosen message–which often enables further attacks (e.g. padding oracles with AES-CBC + HMAC). The cryptographic secret is the correct authentication tag for a chosen message under a key known only to the defender.
- Leaking the number of leading zeroes introduced the risk of lattice attacks in TLS when used with Diffie-Hellman ciphersuites. See also: the Raccoon Attack. The cryptographic secret is the zero-trimmed shared secret, which is an input to a hash function.
- Leaking the secret number
in the modular inverse step when calculating an ECDSA signature gives attackers enough information to recover the secret key. This can happen if you’re using non-constant-time arithmetic.
Timing attacks can even break state-of-the-art cryptography projects, like the algorithms submitted to NIST’s Post-Quantum Cryptography standardization effort:
https://twitter.com/EllipticKiwi/status/1295670085969838080
However–and this is important–if what leaks is a public input (n.b. something the attackers already knows anyway), then who cares?

Why Timing Leaks Don’t Break Signature Verification
If you’re reviewing some cryptography library and discovered a timing leak in the elliptic curve signature verification function, you might feel tempted to file a vulnerability report with the maintainers of the library.
If so, you’re wasting your time and theirs, for two reasons:
- Signature verification is performed over public inputs (message, public key, signature).
- Knowing which byte verification the comparison fails on isn’t sufficient for forging a signature for a chosen message.
The first part is obvious (and discussed above), but the second might seem untrue at first: If HMAC breaks this way, why doesn’t ECDSA also suffer here?
The Anatomy of Elliptic Curve Digital Signatures
Elliptic curve signatures are usually encoded as 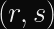
In the case of ECDSA, you calculate two numbers (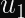

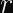

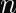
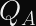
Why Don’t Timing Attacks Do Anything Here?
Even with a timing leak on the string compare function in hand, you cannot easily find a valid 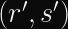
- The derivation of
is effectively an All-Or-Nothing Transform based on secret inputs.
- The curve point equation
) multiplies the ratio r/s by the public key (because
).
In order to calculate a valid 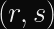
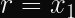
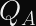
It’s not impossible to calculate this value, but it’s computationally infeasible, and the difficulty of this problem is approximately one fourth the signature size. That is to say, 512-bit signatures, derived from 256-bit keys, have a security level of 128 bits.
Thus, timing leakage won’t let you perform an existential forgery here.

(Art by Khia.)
Under What Conditions Could Timing Side-Channels Matter to ECDSA Verification?
Suppose you have a JSON Web Token library that’s vulnerable to the type confusion attack (wherein you can swap out the "alg":"ES256" with "alg":"HS256" and then use the public key as if it was an HMAC symmetric key).
In this hypothetical scenario, let’s say you’re using this JWT library in an OIDC-like configuration, where the identity provider signs tokens and the application verifies them, using a public key known to the application.
Also assume, for absolutely contrived reasons, that the public key is not known to the attacker.
If you had a timing attack that leaks the public key, that would be a viable (if horrendously slow) way to make the vulnerability exploitable.
However, even in this setup, the timing leak still doesn’t qualify as a real vulnerability. It merely defeats attempts at Security Through Obscurity. The real vulnerability is any JWT library that allows this attack (or alg=none).
Additionally, you can recover the public key if you have sufficient knowledge of the curve algorithm used, message signed, etc.–which you do if the algorithm is ES256–so you don’t really even need a timing leak for this. Consequently, timing leaks would only help you if the original algorithm was something custom and obscure to attackers.
(Aside: there are two possible public keys from each signature, so the signature alone isn’t sufficient for uniquely identifying public keys. If you’re hoping to reduce protocol bandwidth through this trick, it won’t work.)
TL;DR
In order for a timing leak to be useful for cryptanalysis, it cannot leak a publicly-known input to the cryptographic operation.
https://soatok.blog/2021/06/07/dead-ends-in-cryptanalysis-2-timing-side-channels/
#cryptanalysis #crypto #cryptography #deadEndsInCryptanalysis #ECDSA #sideChannels #Technology #timingAttacks
This is the first entry in a (potentially infinite) series of dead end roads in the field of cryptanalysis.Cryptography engineering is one of many specialties within the wider field of security engineering. Security engineering is a discipline that chiefly concerns itself with studying how systems fail in order to build better systems–ones that are resilient to malicious acts or even natural disasters. It sounds much simpler than it is.
If you want to develop and securely implement a cryptography feature in the application you’re developing, it isn’t enough to learn how to implement textbook descriptions of cryptography primitives during your C.S. undergrad studies (or equivalent). An active interest in studying how cryptosystems fail is the prerequisite for being a cryptography engineer.
Thus, cryptography engineering and cryptanalysis research go hand-in-hand.
Pictured: How I feel when someone tells me about a novel cryptanalysis technique relevant to the algorithm or protocol I’m implementing. (Art by Khia.)
If you are interested in exploring the field of cryptanalysis–be it to contribute on the attack side of cryptography or to learn better defense mechanisms–you will undoubtedly encounter roads that seem enticing and not well-tread, and it might not be immediately obvious why the road is a dead end. Furthermore, beyond a few comparison tables on Wikipedia or obscure Stack Exchange questions, the cryptology literature is often sparse on details about why these avenues lead nowhere.
So let’s explore where some of these dead-end roads lead, and why they stop where they do.
(Art by Kyume.)
Length Extension Attacks
It’s difficult to provide a better summary of length extension attacks than what Skull Security wrote in 2012. However, that only addresses “What are they?”, “How do you use them?”, and “Which algorithms and constructions are vulnerable?”, but leaves out a more interesting question: “Why were they even possible to begin with?”An Extensive Tale
Tale, not tail! (Art by Swizz.)
To really understand length extension attacks, you have to understand how cryptographic hash functions used to be designed. This might sound intimidating, but we don’t need to delve too deep into the internals.
A cryptographic hash function is a keyless pseudorandom transformation from a variable length input to a fixed-length output. Hash functions are typically used as building blocks for larger constructions (both reasonable ones like HMAC-SHA-256, and unreasonable ones like my hash-crypt project).
However, hash functions like SHA-256 are designed to operate on sequential blocks of input. This is because sometimes you need to stream data into a hash function rather than load it all into memory at once. (This is why you can sha256sum a file larger than your available RAM without crashing your computer or causing performance headaches.)
A streaming hash function API might look like this:
class MyCoolHash(BaseHashClass): @staticmethod def init(): """ Initialize the hash state. """ def update(data): """ Update the hash state with additional data. """ def digest(): """ Finalize the hash function. """ def compress(): """ (Private method.) """
To use it, you’d callhash = MyCoolHash.init()and then chain togetherhash.update()calls with data as you load it from disk or the network, until you’ve run out of data. Then you’d calldigest()and obtain the hash of the entire message.There are two things to take away right now:
- You can call
update()multiple times, and that’s valid.- Your data might not be an even multiple of the internal block size of the hash function. (More often than not, it won’t be!)
So what happens when you call
digest()and the amount of data you’ve passed toupdate()is not an even multiple of the hash size?For most hash functions, the answer is simple: Append some ISO/IEC 7816-4 padding until you get a full block, run that through a final iteration of the internal compression function–the same one that gets called on
update()–and then output the current internal state.Let’s take a slightly deeper look at what a typical runtime would look like for the MyCoolHash class I sketched above:
hash = MyCoolHash.init()
- Initialize some variables to some constants (initialization vectors).
hash.update(blockOfData)
- Start with any buffered data (currently none), count up to 32 bytes. If you’ve reached this amount, invoke
compress()on that data and clear the buffer. Otherwise, just append blockOfData to the currently buffered data.- For every 32 byte of data not yet touched by
compress(), invokecompress()on this block (updating the internal state).- If you have any leftover bytes, append to the internal buffer for the next invocation to process.
hash.update(moreData)
- Same as before, except there might be some buffered data from step 2.
output = hash.digest()
- If you have any data left in the buffer, append a 0x80 byte followed by a bunch of 0x00 bytes of padding until you reach the block size. If you don’t, you have an entire block of padding (0x80 followed by 0x00s).
- Call
compress()one last time.- Serialize the internal hash state as a byte array or hexadecimal-encoded string (depending on usage). Return that to the caller.
This is fairly general description that will hold for most older hash functions. Some details might be slightly wrong (subtly different padding scheme, whether or not to include a block of empty padding on
digest()invocations, etc.).The details aren’t super important. Just the rhythm of the design.
init()update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
update()
- load buffer,
compress()compress()compress()- …
- buffer remainder
- …
digest()
- load buffer, pad,
compress()- serialize internal state
- return
And thus, without having to know any of the details about what
compress()even looks like, the reason why length extension attacks were ever possible should leap out at you!
Art by Khia.
If it doesn’t, look closely at the difference between
update()anddigest().There are only two differences:
update()doesn’t pad before callingcompress()digest()returns the internal state thatcompress()always mutatesThe reason length-extension attacks are possible is that, for some hash functions, the output of
digest()is its full internal state.This means that you can run take an existing hash function and pretend it’s the internal state after an
update()call instead of adigest()call by appending the padding and then, after callingcompress(), appending additional data of your choice.The (F)Utility of Length Extension
Length-Extension Attacks are mostly used for attacking naive message authentication systems where someone attempts to authenticate a message (M) with a secret key (k), but they construct it like so:
auth_code = vulnerable_hash(k.append(M))
If this sounds like a very narrow use-case, that’s because it is. However, it still broke Flickr’s API once, and it’s a popular challenge for CTF competitions around the world.Consequently, length-extension attacks are sometimes thought to be vulnerabilities of the construction rather than a vulnerability of the hash function. For a Message Authentication Code construction, these are classified under canonicalization attacks.
After all, even though SHA-256 is vulnerable to length-extension, but you can’t actually exploit it unless someone is using it in a vulnerable fashion.
That being said, it’s often common to say that hash functions like SHA-256 and SHA-512 are prone to length-extension.
Ways to Avoid Length-Extension Attacks
Use HMAC. HMAC was designed to prevent these kinds of attacks.Alternatively, if you don’t have any cryptographic secrets, you can always do what bitcoin did: Hash your hash again.
return sha256(sha256(message))
Note: Don’t actually do that, it’s dangerous for other reasons. You also don’t want to take this to an extreme. If you iterate your hash too many times, you’ll reinvent PBKDF1 and its insecurity. Two is plenty.Or you can do something really trivial (which ultimately became another standard option in the SHA-2 family of hash functions):
Always start with a 512-bit hash and then truncate your output so the attacker never recovers the entire internal state of your hash in order to extend it.
That’s why you’ll sometimes see SHA-512/224 and SHA-512/256 in a list of recommendations. This isn’t saying “use one or the other”, that’s the (rather confusing) notation for a standardized SHA-512 truncation.
Note: This is actually what SHA-384 has done all along, and that’s one of the reasons why you see SHA-384 used more than SHA-512.
If you want to be extra fancy, you can also just use a different hash function that isn’t vulnerable to length extension, such as SHA-3 or BLAKE2.
Questions and Answers
Art by Khia.
Why isn’t BLAKE2 vulnerable to length extension attacks?
Quite simply: It sets a flag in the internal hash state before compressing the final buffer.If you try to deserialize this state then invoke
update(), you’ll get a different result than BLAKE2’scompress()produced duringdigest().For a secure hash function, a single bit of difference in the internal state should result in a wildly different output. (This is called the avalanche effect.)
Why isn’t SHA-3 vulnerable to length extension attacks?
SHA-3 is a sponge construction whose internal state is much larger than the hash function output. This prevents an attacker from recovering the hash function’s internal state from a message digest (similar to the truncated hash function discussed above).Why don’t length-extension attacks break digital signature algorithms?
Digital signature algorithms–such as RSASSA, ECDSA, and EdDSA–take a cryptographic hash of a message and then perform some asymmetric cryptographic transformation of the hash with the secret key to produce a signature that can be verified with a public key. (The exact details are particular to the signature algorithm in question.)Length-extension attacks only allow you to take a valid H(k || m) and produce a valid H(k || m || padding || extra) hash that will validate, even if you don’t know k. They don’t magically create collisions out of thin air.
Even if you use a weak hash function like SHA-1, knowing M and H(M) is not sufficient to calculate a valid signature. (You need to be able to know these values in order to verify the signature anyway.)
The security of digital signature algorithms depends entirely on the secrecy of the signing key and the security of the asymmetric cryptographic transformation used to generate a signature. (And its resilience to side-channel attacks.)
However, a more interesting class of attack is possible for systems that expect digital signatures to have similar properties as cryptographic hash functions. This would qualify as a protocol vulnerability, not a length-extension vulnerability.
TL;DR
Art by Khia.
Length-extension attacks exploit a neat property of a few cryptographic hash functions–most of which you shouldn’t be using in 2020 anyway (SHA-2 is still fine)–but can only be exploited by a narrow set of circumstances.
If you find yourself trying to use length-extension to break anything else, you’ve probably run into a cryptographic dead end and need to backtrack onto more interesting avenues of exploitation–of which there are assuredly many (unless your cryptography is boring).
Next: Timing Side-Channels
https://soatok.blog/2020/10/06/dead-ends-in-cryptanalysis-1-length-extension-attacks/
#cryptanalysis #crypto #cryptographicHashFunction #cryptography #lengthExtensionAttacks


