If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.

I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.

This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.

To be clear: This is solely my opinion and not representative of any company or academic institution.

What is AES-GCM?

AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.

In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.

What is AES?

The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.

Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.

AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.

As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.

This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)

Why AES Sucks

Art by Khia.

Side-Channels

The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).

There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.

The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.

Block Size

AES-128 is considered by experts to have a security level of 128 bits.

Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.

However, the AES block size is only 128 bits!

That might not sound like a big deal, but it severely limits the constructions you can create out of AES.

Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.

This means you expect a collision after encrypting 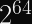(at 50% probability) blocks.

When you start getting collisions, you can break CBC mode, as this video demonstrates:

https://www.youtube.com/watch?v=v0IsYNDMV7A

This is significantly smaller than the you expect from AES.

Post-Quantum Security?

With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.

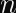
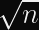
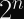
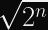
This is because Grover’s quantum search algorithm can search unsorted items in time, which can be used to reduce the total number of possible secrets from to . This effectively cuts the security level, expressed in bits, in half.

Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.

But remember, even AES-256 operates on 128-bit blocks.

Consequently, for AES-256, there should be approximately (plaintext, key) pairs that produce any given ciphertext block.

Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)

Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are times as many AES-256 keys as there are possible plaintext/ciphertexts. Keep this in mind for AES-GCM.

This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.

This would not be nearly as much of a problem if AES’s block size was 256 bits.

Real-World Example: Signal

The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.

Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.

Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.

The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).

Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.

Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.

However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.

This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.

This is unacceptable!

What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.

As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.

Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.

Why AES-GCM Sucks Even More

AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.

AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:

1. The plaintext message.
2. The encryption key.
3. A nonce (: A number that must only be used once).
4. Optional additional data which will be authenticated but not encrypted.

The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.

Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.

That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.

The deeper you look into AES-GCM’s design, the harder you will feel this sticker.

GHASH Brittleness

The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called . This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
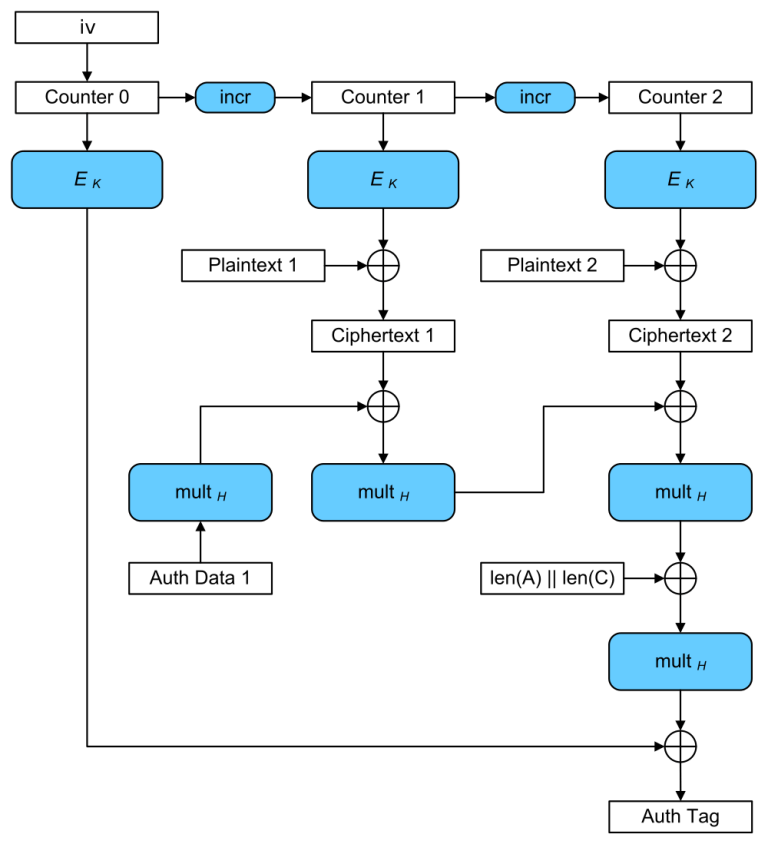
This is often sold as an advantage: Reusing allows for better performance. However, it makes GCM brittle: Reusing a nonce allows an attacker to recover H and then forge messages forever. This is called the “forbidden attack”, and led to real world practical breaks.

Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.

ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.

While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.

Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.

H Reuse and Multi-User Security

If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.

If we assume AES is well-behaved, we can deduce that there are approximately different 256-bit keys that will map a single plaintext block to a single ciphertext block.

This is trivial to calculate. Simply divide the number of possible keys (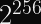) by the number of possible block states () to yield the number of keys that produce a given ciphertext for a single block of plaintext: .

Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately .

This means there are approximately independent keys that will map a given all-zero plaintext block to an arbitrarily chosen value of (if we assume AES doesn’t have weird biases).

Credit: Harubaki

“Why Does This Matter?”

It means that, with keys larger than 128 bits, you can model the selection of as a 128-bit pseudorandom function, rather than a 128-bit permutation. As a result, you an expect a collision with 50% probability after only different keys are selected.

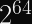
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.

But 50% isn’t good enough for cryptographic security.

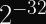
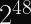
In most real-world systems, we target a collision risk. So that means our safety limit is actually different AES keys before you have to worry about reuse.

This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of 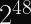different AES keys, you have to either accept the risk or stop using AES-GCM.

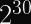
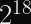
If you have a billion users (), the safety limit is breached after AES keys per user (approximately 262,000).

“What Good is H Reuse for Attackers if HF differs?”

There are two numbers used in AES-GCM that are derived from the AES key. is used for block multiplication, and (the value of with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.

The arrow highlighted with green is HF.

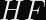
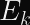
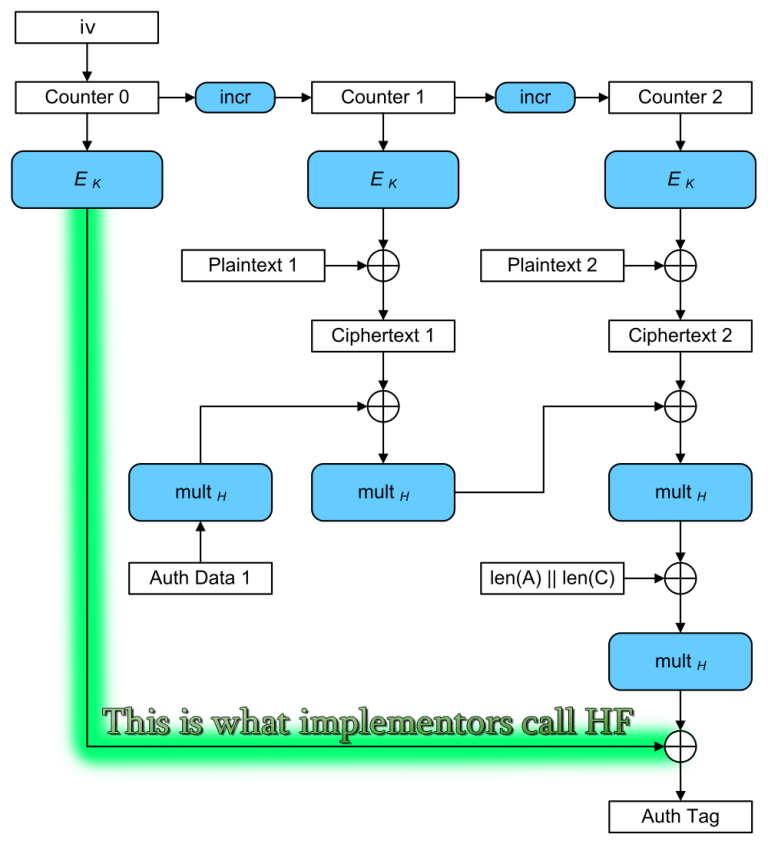
It’s tempting to think that a reuse of isn’t a concern because will necessarily be randomized, which prevents an attacker from observing when collides. It’s certainly true that the single-block collision risk discussed previously for will almost certainly not also result in a collision for . And since isn’t reused unless a nonce is reused (which also leaks directly), this might seem like a non-issue.

Art by Khia.

However, it’s straightforward to go from a condition of reuse to an adaptive chosen-ciphertext attack.

1. Intercept multiple valid ciphertexts.
   
   • e.g. Multiple JWTs encrypted with {"alg":"A256GCM"}

   
   

2. Use your knowledge of , the ciphertext, and the AAD to calculate the GCM tag up to the final XOR. This, along with the existing authentication tag, will tell you the value of for a given nonce.
3. Calculate a new authentication tag for a chosen ciphertext using and your candidate value, then replay it into the target system.

While the blinding offered by XORing the final output with 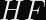is sufficient to stop from being leaked directly, the protection is one-way.

Ergo, a collision in is not sufficiently thwarted by .

“How Could the Designers Have Prevented This?”

The core issue here is the AES block size, again.

If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.

However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.

NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).

“Why Isn’t This a Vulnerability?”

There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.

Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).

With AES-GCM, the expected distance between collisions in is , and finding an untargeted collision requires being able to observe more than different sessions, and somehow distinguish when collides.

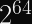
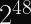
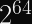
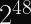
As a user, you know that after different keys, you’ve crossed the safety boundary for avoiding collisions. But as an attacker, you need bites at the apple, not . Additionally, you need some sort of oracle or distinguisher for when this happens.

We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide is challenging to work with. You would need the computational and data storages of a major cloud service provider to even think about pulling the attack off.

Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.

Short Nonces

Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.

(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)

If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.

1. Message Length Limit: AES-GCM can be used to encrypt messages up to bytes long, under a given (key, nonce) pair.
2. Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after messages.
   However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM at random nonces, which represents a collision probability of one in 4 billion.

These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.

Random Key Robustness

Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).

You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.

Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.

Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.

Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.

This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)

Better-Designed Algorithms

You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”

I’m glad you asked!

XChaCha20-Poly1305

For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.

• ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
• ChaCha20 is ChaCha with 20 rounds.
• XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about messages (for the same collision probability as AES-GCM).
• Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
• XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.

For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.

However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.

The Gimli Permutation

For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.

Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.

Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.

Closing Remarks

Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.

Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.

Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.

My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.

We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.

Change Log

• 2021-10-26: Added section on H Reuse and Multi-User Security.

https://soatok.blog/2020/05/13/why-aes-gcm-sucks/

#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography

Dhole Moments

2020-07-12 21:33:27

There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.

Today, we’re going to look at how some symmetric encryption methods stack up against each other.

If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.

Comparisons

• AES-GCM vs. ChaCha20-Poly1305
• AES-GCM vs. XChaCha20-Poly1305
• AES-GCM vs. AES-CCM
• AES-GCM vs. AES-GCM-SIV
• AES-GCM vs. AES-SIV
• AES-GCM-SIV vs. AES-SIV
• AES-GCM vs. AES-CBC
• AES-GCM vs. AES-CTR
• AES-CBC vs. AES-CTR
• AES-CBC vs. AES-ECB
• AES vs. Blowfish
• ChaCha vs. Salsa20
• ChaCha vs. RC4
• Cipher Cascades

AES-GCM vs. ChaCha20-Poly1305

• If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
• Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
• AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
• Nonce size:
  
  • AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
  • ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).

  
  

• Wearout of a single (key, nonce) pair:
  
  • AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
  • ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).

  
  

• Neither algorithm is nonce misuse resistant.

Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.

Back to the top

AES-GCM vs. XChaCha20-Poly1305

• XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
• To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
• The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.

Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.

Back to the top

AES-GCM vs. AES-CCM

AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.

Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.

Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).

A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.

Conclusion: Just use AES-GCM.

Back to the top

AES-GCM vs. AES-GCM-SIV

AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.

Nonce misuse resistance is really cool. (Art by Swizz)

The algorithms are significantly different:

• AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
• AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)

AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.

So really, use which ever you want.

Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?

https://twitter.com/colmmacc/status/986286693572493312

Conclusion: AES-GCM-SIV is better, but both are fine.

Back to the top

AES-GCM vs. AES-SIV

At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:

• Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
• AES-SIV is MAC then encrypt (so is AES-CCM).
• AES-SIV uses AES-CTR (so does AES-CCM).

If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.

AES-GCM also has the added advantage of not relying on CBC-MAC.

Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.

Back to the top

AES-GCM-SIV vs. AES-SIV

If you read the previous two sections, the conclusion here should be obvious.

• AES-GCM-SIV is slightly better than AES-GCM.
• AES-GCM is better than AES-SIV.

Conclusion: Use AES-GCM-SIV.

Back to the top

AES-GCM vs. AES-CBC

Just use AES-GCM. No contest.

AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).

If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).

If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:

1. encKey := HmacSha256(“encryption-cbc-hmac”, key)
2. macKey := HmacSha256(“authentication-cbc-hmac”, key)
3. iv := RandomBytes(16)
4. ciphertext := AesCbc(plaintext, iv, encKey)
5. tag := HmacSha256(iv + ciphertext, macKey)

For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.

There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.

AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.

The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.

Back to the top

AES-GCM vs. AES-CTR

Just use AES-GCM. No contest.

Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.

If you must use AES-CTR, the same rules apply as for AES-CBC:

1. encKey := HmacSha256(“encryption-ctr-hmac”, key)
2. macKey := HmacSha256(“authentication-ctr-hmac”, key)
3. nonce := RandomBytes(16)
4. ciphertext := AesCtr(plaintext, nonce, encKey)
5. tag := HmacSha256(nonce + ciphertext, macKey)

For decryption you need a secure compare function.

AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.

Back to the top

AES-CBC vs. AES-CTR

If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.

That being said:

AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.

AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.

If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.

Back to the top

AES-CBC vs. AES-ECB

Never use ECB mode. ECB mode lacks semantic security.

Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.

Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.

Back to the top

AES vs. Blowfish

A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:

Why?! (Art by Khia)

Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”

Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.

AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.

AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.

Conclusion: Use AES instead of Blowfish.

Back to the top

ChaCha vs. Salsa20

Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.

That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.

Conclusion: Your choice (both are good but ChaCha is slightly better).

Back to the top

ChaCha vs. RC4

Don’t use RC4 for anything! What are you doing?

My reaction when I read that the CIA was using a modified RC4 in their Assassin malware instead of a secure stream cipher, per the Vault7 leaks. (Art by Khia)

RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.

Conclusion: Use ChaCha. Never use RC4.

Back to the top

Cipher Cascades

A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).

Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.

If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.

Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.

Back to the top

Symmetric Encryption Rankings

So with all of the above information, can we rank these algorithms into tiers?

Art by Riley

Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.

S	XChaCha20-Poly1305, AES-GCM-SIV
A	AES-GCM, ChaCha20-Poly1305
B	AES-SIV
C	AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2
D	AES-CCM
F	Any: AES-ECB, RC4, Blowfish Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaCha

Soatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/

#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305