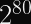Search
Items tagged with: AESGCM
Ever since the Invisible Salamanders paper was published, there has been a quiet renaissance within my friends and colleagues in applied cryptography for studying systems that use Authenticated Encryption with Associated Data (AEAD) constructions, understanding what implicit assumptions these systems make about the guarantees of the AEAD mode they chose to build upon, and the consequences of those assumptions being false.
I’ve discussed Invisible Salamanders several times throughout this blog, from my criticisms of AES-GCM and XMPP + OMEMO to my vulnerability disclosures in Threema.
Five years after Invisible Salamanders, it’s become clear to me that many software developers do not fully appreciate the underlying problem discussed in the Invisible Salamanders paper, even when I share trivial proof-of-concept exploits.
Background
Fast AEAD constructions based on polynomial MACs, such as AES-GCM and ChaCha20-Poly1305, were designed to provide confidentiality and integrity for the plaintext data, and optionally integrity for some additional associated data, in systems where both parties already negotiated one shared symmetric key.
The integrity goals of the systems that adopted these AEAD constructions were often accompanied by performance goals–usually to prevent Denial of Service (DoS) attacks in networking protocols. Verification needed to be very fast and consume minimal resources.
In this sense, AEAD constructions were an incredible success. So successful, in fact, that most cryptographers urge application developers to use one of the fast AEAD modes as the default suggestion without looking deeper at the problem being solved. This is a good thing, because most developers will choose something stupid like ECB mode in the absence of guidance from cryptographers, and AEAD modes are much, much safer than any hand-rolled block cipher modes.
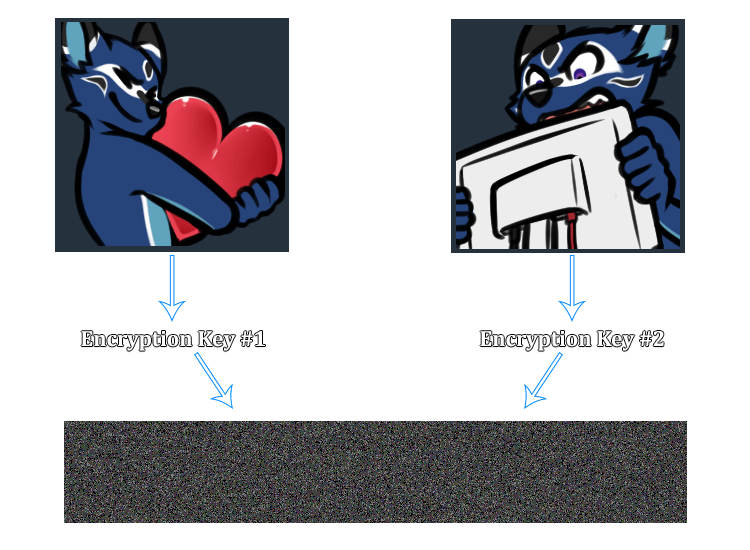
The problem is, that one tiny little assumption that both parties (sender, recipient) for a communication have agreed on exactly one symmetric key for use in the protocol.
Fast MACs Are Not Key-Committing
Cryptographers have concluded that AEAD constructions based on polynomial MACs–while great for performance and rejection of malformed packets without creating DoS risks–tend to make the same assumption. This is even true of misuse-resistant modes like AES-GCM-SIV and extended-nonce constructions like XSalsa20-Poly1305.
When discussing this implicit assumption of only one valid key in the systems that use these AEAD modes, we say that the modes are not key-committing. This terminology is based on what happens when this assumption is false.
Consequently, you can take a single, specially crafted ciphertext (with an authentication tag) and decrypt it under multiple different keys. The authentication tags will be valid for all keys, and the plaintext will be different.
What does this look like in practice?
Consider my GCM exploit, which was written to generate puzzle ciphertexts for the DEFCON Furs badge challenge a few years ago. How it works is conceptually simple (although the actual mechanics behind step 4 is a bit technical):
- Generate two keys.
There’s nothing special about these keys, or their relationship to each other, and can be totally random. They just can’t be identical or the exploit is kind of pointless. - Encrypt some blocks of plaintext with key1.
- Encrypt some more blocks of plaintext with key2.
- Calculate a collision block from the ciphertext in the previous two steps–which is just a bit of polynomial arithmetic in GF(2^128)
- Return the ciphertext (steps 2, 3, 4) and authentication tag calculated over them (which will collide for both keys).
A system that decrypts the output of this exploit under key1 will see some plaintext, followed by some garbage, followed by 1 final block of garbage.
If the same system decrypts under key2, it will see some garbage, followed by some plaintext, followed by 1 final block of garbage.
For many file formats, this garbage isn’t really a problem. Additionally, a bit more precomputation allows you to choose garbage that will be more advantageous to ensuring both outputs are accepted as “valid” by the target system.
For example, choosing two keys and a targeted nonce may allow both the valid plaintext and garbage blocks to begin with a PDF file header.
If you’re familiar with the file polyglot work of Ange Albertini, you can use this to turn the Invisible Salamanders problem into an artform.
And this is just the simple attack!
The Invisible Salamanders paper outlined a more advanced variant (with a proof of concept) in Section 3.2, which doesn’t suffer from nearly as much garbage data as the simple attack.
As Bruce Schneier often says, “Attacks only get better, they never get worse.”
Why is it called Invisible Salamanders?
The proof-of-concept used in the paper involved sending one picture (of a salamander) over an end-to-end encrypted messaging app, but when the recipient flagged it as abusive, the moderator saw a different picture.
https://www.youtube.com/watch?v=3M1jIO-jLHI
Thus, the salamander was invisible to the moderators of the encrypted messaging app.
As for the choice of a “salamander”, I’ve been told by friends familiar with the research that was inspired by the original name of the Signal Protocol being “Axolotl”.
But, like, who cares about these details besides me? It’s a cute and memorable name.
What are the consequences of violating the “one key” assumption?
That depends entirely on what your system does!
In Database Cryptography Fur the Rest of Us, I discussed the use of AEAD modes to prevent confused deputy attacks. This works great, but if you’re building an application that supports multi-tenancy, you suddenly have to care about this issue again.
An earlier design for OPAQUE, a password authenticated key exchange algorithm, was broken by a partitioning oracle attack due to building atop AEAD modes that are not key-committing. This let an attacker recover passwords from Shadowsocks proxy servers with a complexity similar to a binary search algorithm.
These are two very different impacts from the same weakness, which I believe is a significant factor for why the Invisible Salamanders issue isn’t more widely understood.
Sometimes violating the “one key” assumption that went into fast AEAD modes based on Polynomial MACs completely destroys the security of your system.
Other times, it opens the door for a high-complexity but low-impact behavior that simply violates the principle of least astonishment but doesn’t buy the attacker anything useful.
They Just Don’t Get It
The Invisible Salamanders issue is relevant in any system that uses symmetric-key encryption where more than one key can be valid.
This includes, but is not limited to:
- Multi-tenant data warehouses
- Group messaging protocols
- It’s sometimes tempting to discount group messaging as a relevant consideration if your experience is “emulated groups atop 1-to-1 messaging”, but there are protocols that establish a Group Key (i.e., RFC 9420) and then use that for all group messages.
- Envelope encryption schemes with multiple wrapping keys
- Bearer tokens (such as JSON Web Tokens) in systems that utilize Key IDs
Systems can mitigate this issue by introducing an explicit key commitment scheme (based on a cryptographic hash rather than a polynomial MAC) or by using a committing cipher mode (such as AES + HMAC, if done carefully).
However, most of the time, this advice falls on deaf ears whenever this concern is brought up by a cryptography engineer who’s more aware of this issue.
“Abuse reporting? We don’t have no stinking abuse reporting!”
The most common misunderstanding is, “We don’t have a report abuse feature, so this issue doesn’t affect us.”
This is because the Invisible Salamanders talk and paper focused on how it could be leveraged to defeat abuse reporting tools and bypass content moderation.
In my experience, many security teams would read the paper and conclude that it only impacts abuse reporting features and not potentially all systems that allow multiple symmetric keys in a given context.
Another Exploit Scenario
Imagine you’re building a Data Loss Prevention product that integrates with corporate file-sharing and collaboration software (e.g. ownCloud) for small and medium businesses.
One day, someone decides to ship an end-to-end encryption feature to the file-sharing software that uses AES-GCM to encrypt files, and then encrypts the keys to each recipient’s public key. This is basically the envelope encryption use-case above.
So, you dutifully update your integration to act as another “user”, whose public key must be included in all E2EE transfers, and will block download of ciphertexts it cannot decrypt OR contains sensitive information.
And this works, until an insider threat clever enough to abuse the Invisible Salamanders issue comes along.
In order for said insider threat (e.g., a senior business analyst) to leak sensitive data (e.g., anything that would be useful for illegal insider trading) to another person that shouldn’t have access to it (e.g., a store clerk that’s talking to the press), they just have to do this:
- Encrypt the data they want to exfiltrate using key1.
- Encrypt some innocuous data that won’t trigger your DLP product, using key2.
- Ensure that both messages encrypt to the same ciphertext and authentication tag.
- Give their recipient key1, give everyone else (including your DLP software) key2.
Bam! File leaked, and everyone’s none the wiser, until it’s too late. Let’s actually imagine what happens next:
A random store clerk has leaked sensitive data to the press that only a few analysts had access to.The only communication between the analyst and the store clerk is a file that was shared to all employees, using the E2EE protocol. No emails or anything else were identified.
Your DLP product didn’t identify any other communications between these two, but somehow the store clerk has the data on their desktop.
A detailed forensics analysis may eventually figure out what happened, but by then, the damage is done and your product’s reputation is irrecoverably damaged.
All because the hypothetical E2EE protocol didn’t include a key-commitment mechanism, and nobody identified this deficit in their designs.
This isn’t to endorse DLP solutions at all, but rather, to highlight one of the many ways that the Invisible Salamander issue can be used creatively by clever attackers.
“Couldn’t you do the same with steganography?”
No, the attack is very different from stego.
Stego is about hiding a message in plain sight, so that only the person that knows where/how to look can find it.
The Invisible Salamanders attack lets you send one ciphertext through a network then selectively decrypt it to one of two plaintexts, depending on which key you reveal to each participant.
In the Invisible Salamanders paper and talk, they used this to send “abusive” messages to a recipient that the moderator would not see. Thus, invisible.
In one, the message is always emitted to anyone who knows how to find it. In the other, the attacker selects which you see, even if you have mechanisms to ensure you’re seeing the same ciphertext. It’s not a subtle difference.
Mitigation Techniques
There are multiple ways to mitigate the risk of Invisible Salamanders in a cryptosystem.
- Use HMAC, or (failing that) something built atop cryptographic hash functions, rather than a Polynomial MAC.
- Use an AEAD cipher designed with multi-recipient integrity as a security goal.
- Compute a non-invertible, one-way commitment of the encryption key.
A trivial mitigation looks like this:
class SoatokExampleEncryptor { const NEW_ENCRYPT_KEY = 'myProtocol$encryptKey'; const NEW_COMMITMENT = 'myProtocol$commitment'; public function __construct(#[SensitiveParameter] private string $key) {} /** * Let's assume we're starting with a simple AES-GCM wrapper */ public function legacyEncrypt(string $plaintext, string $assocData = ''): string { $nonce = random_bytes(12); $tag = ''; $ciphertext = openssl_encrypt( $plaintext, 'aes-256-gcm', $this->key, OPENSSL_RAW_DATA, $nonce, $tag, $assocData ); return $nonce . $ciphertext . $tag; } /** * An improved function looks something like this */ public function newEncrypt(string $plaintext, string $assocData = ''): string { // Avoid birthday bound issues with 256-bits of randomness $longerNonce = random_bytes(32); // Derive a subkey and synthetic nonce $tmp = hash_hkdf('sha512', $this->key, 44, self::NEW_ENCRYPT_KEY . $longerNonce); $encKey = substr($tmp, 0, 32); $nonce = substr($tmp, 32); // New: Key commitment $commitment = hash_hkdf('sha512', $this->key, 32, self::NEW_COMMITMENT . $longerNonce); // Most of this is unchanged $tag = ''; $ciphertext = openssl_encrypt( $plaintext, 'aes-256-gcm', $encKey, OPENSSL_RAW_DATA, $nonce, $tag, $assocData ); return $longerNonce . $commitment . $ciphertext . $tag; }}
And then the decryption logic would recalculate the commitment, and compare it with the stored value, in constant-time.
It’s important that the commitment be stored with the ciphertext, rather than bundling it with the key.
(It may be worthwhile to also include the commitment in the associated data, to add a mechanism against downgrade attacks.)
The Lesson to Learn
If you’re building a network protocol that uses AEAD to encrypt data over an insecure network (e.g., WireGuard), keep up the good work.
If you’re doing anything more involved than that, at the application layer, pause for a moment and consider whether your system will ever need multiple valid symmetric keys at once.
And, if the answer is “yes”, then you should always explicitly add a key-commitment mechanism to your system design.
(Hire a cryptographer if you’re not sure how to proceed.)
In my opinion, hemming and hawing over whether there’s a significant impact to the Invisible Salamanders issue is a worse use of your time than just solving it directly.
Eventually, I expect a new generation of AEAD modes will be standardized that explicitly provide key-commitment.
When these new designs are standardized, widely supported, and sufficiently trusted by experts, feel free to update my advice to “prefer using those modes” instead.
Header art: Harubaki, CMYKat, and a photo by Brian Gratwicke. Poorly photoshopped by myself.
https://soatok.blog/2024/09/10/invisible-salamanders-are-not-what-you-think/
#AEAD #AESGCM #InvisibleSalamanders #randomKeyRobustness #symmetricCryptography
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Art by Khia.
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting
(at 50% probability) blocks.
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
you expect from AES.
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.This is because Grover’s quantum search algorithm can search
unsorted items in
time, which can be used to reduce the total number of possible secrets from
to
. This effectively cuts the security level, expressed in bits, in half.
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Hooray for well-engineered protocols managing to actually protect users.
Art by Swizz.However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
This is unacceptable!
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
: A number that must only be used once).
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
The deeper you look into AES-GCM’s design, the harder you will feel this sticker.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called. This value is used for authenticating all messages authenticated under that AES key, rather than for a given (key, nonce) pair.
Diagram describing Galois/Counter Mode, taken from Wikipedia.
This is often sold as an advantage: ReusingLet’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.If we assume AES is well-behaved, we can deduce that there are approximately
This is trivial to calculate. Simply divide the number of possible keys (
) by the number of possible block states (
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
This means there are approximately
Credit: Harubaki
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection ofNote: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a
collision risk. So that means our safety limit is actually
different AES keys before you have to worry about
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of
If you have a billion users (
), the safety limit is breached after
AES keys per user (approximately 262,000).
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.(the value of
with a counter of 0 from the following diagram) is XORed with the final result to produce the authentication tag.
The arrow highlighted with green is HF.
It’s tempting to think that a reuse of
Art by Khia.
However, it’s straightforward to go from a condition of
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- Use your knowledge of
- Calculate a new authentication tag for a chosen ciphertext using
While the blinding offered by XORing the final output with
Ergo, a collision in
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
As a user, you know that after
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
bytes long, under a given (key, nonce) pair.
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atrandom nonces, which represents a collision probability of one in 4 billion.
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
I’m glad you asked!
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
messages (for the same collision probability as AES-GCM).
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography
Spyware written for educational institutions to flex their muscles of control over students and their families when learning from their home computer is still, categorically, spyware.
Depending on your persuasion, the previous sentence sounds like either needless pedantry, or it reads like tautology. But we need to be clear on our terms.
- Educational spyware is still spyware.
- Spyware is categorized as a subset of malware.
When vulnerabilities are discovered in malware, the normal rules of coordinated disclosure are out of scope. Are we clear?
So let’s talk about Proctorio!
https://twitter.com/Angry_Cassie/status/1301360994044850182
I won’t go into the details of Proctorio or why it’s terrible for (especially disadvantaged) students. Read Cassie’s Twitter thread for more context on that. Seriously. I’m not gonna be one of those guys that talks over women, and neither should you.
What I am here to talk about today is these dubious claim about the security of their product:
Zero-Knowledge Encryption? OMGWTFBBQ!
In cryptography, there are a class of algorithms called Zero-Knowledge Proofs. In a Zero-Knowledge Proof, you prove that you possess some fact without revealing any details about the fact.
It’s kind of abstract to think about (and until we’re ready to talk about Pedersen commitments, I’m just going to defer to Sarah Jamie Lewis), but the only thing you need to know about “Zero Knowledge” in Cryptography is that the output is a boolean (True, False).
You can’t use “Zero Knowledge” anything to encrypt. So “Zero-Knowledge Encryption” is a meaningless buzzword.
https://twitter.com/SchmiegSophie/status/1304407483658592256
So what are they actually describing when they say Zero Knowledge Encryption?
Okay, so they’ve built their own key distribution system and are encrypting with AES-GCM… and shipped this in a Chrome extension. But before we get to that, look at this Daily Vulnerability Tests claim.
Running Nessus (or equivalent) on a cron job isn’t meaningful metric of security. At best, it creates alert fatigue when you accidentally screw up a deployment configuration or forget to update your software for 4+ years. (Y’know, like JsZip 3.2.1, which they bundle.)
A dumb vulnerability scan isn’t the same thing as a routine (usually quarterly) penetration test or a code audit. And if you’re working in cryptography, you better have both!
Timing Leaks in Proctorio’s AES-GCM Implementation
If you download version 1.4.20241.1.0 of the Proctorio Chrome Extension, run src/assets/J5HG.js through a JS beautifier, and then look at its contents, you will quickly realize this is a JavaScript cryptography library.
Since the “zero knowledge” encryption they’re so proud about uses AES-GCM, let’s focus on that.
Proctorio’s AES-GCM implementation exists in an object called dhs.mode.gcm, which is mildly obfuscated, but contains the following functions:
encrypt()– Encrypt with AES-GCMdecrypt()– Decrypt with AES-GCMaa()– GHASH block multiplicationj()– XOR + GMAC utility functionO()– Called by encrypt() and decrypt(); does all of the AES-CTR + GMAC fun
If you’re not familiar with AES-GCM, just know this: Timing leaks can be used to leak your GMAC key to outside applications, which completely breaks the authentication of AES-GCM and opens the door to chosen-ciphertext attacks.
So is their implementation of AES-GCM constant-time? Let’s take a look at aa():
aa: function(a, b) { var c, d, e, f, g, h = dhs.bitArray.ba; for (e = [0, 0, 0, 0], f = b.slice(0), c = 0; 128 > c; c++) { for ( (d = 0 !== (a[Math.floor(c / 32)] & 1 << 31 - c % 32)) && (e = h(e, f)), g = 0 !== (1 & f[3]), d = 3; d > 0; d-- ) f[d] = f[d] >>> 1 | (1 & f[d - 1]) << 31; f[0] >>>= 1, g && (f[0] ^= -520093696) } return e},
This is a bit obtuse, but this line leaks the lowest bit of f with each iteration: g = 0 !== (1 & f[3]).
Since f gets bitwise right-shifted 128 times, this actually leaks the bit of every value of f in each block multiplication, since the execution of (f[0] ^= -520093696) depends on whether or not g is set to true.
Also, they claim to be FIPS 140-2 compliant, but this is how they generate randomness in their cryptography library.
https://twitter.com/SoatokDhole/status/1304623361461547009
(Although, that’s probably a lie.)
To mitigate these vulnerabilities, one needs look no further than the guide to side-channel attacks I published last month.
(Also, use WebCrypto to generate entropy! What the fuck.)
If Proctorio is Insecure, What Should We Use Instead?
Nothing.
Schools that demand students install spyware on their personal computers are only a step removed from domestic abusers who install stalkerware on their victims’ phones.
Proctorio isn’t the problem here, they’re only a symptom.
Schools that insist on violating the integrity and parental dominion of their students’ home computers are the problem here.
https://twitter.com/lex_about_sex/status/1304156305398140928
If you want to ensure the integrity of students’ education, try teaching them about consent and ethical computing. (Y’know, concepts that are fundamentally incompatible with the business model of Proctorio and Proctorio’s competitors.)
Disclosure Timeline
Really? Really?
This was a zero-day disclosure, because full disclosure is the responsible choice when dealing with spyware. Don’t even @ me.
Domains to Sinkhole
If you’re looking to protect your home network from this spyware, here are a list of domains to sinkhole (i.e. with Pi-Hole).
- proctorauth.com
- proctordata.com
- getproctorio.com
- proctor.io
- proctor.in
- az545770.vo.msecnd.net
Update (2020-09-16): AES in a Hole
I got curious about the security of how they were encrypting data, not just the authentication of that encrypted data.
After all, if Proctorio decided to home-bake GCM in an insecure way, it’s overwhelmingly likely that they rolled their own AES implementation too.
Interlude: Software AES
Implementing AES in software is terrifying. Even moreso in JavaScript, since your code might be secure in a Node.js environment but insecure in a web browser–or vice versa! And you have no way of knowing as a JavaScript developer because you can’t verify the interpreter.
At the risk of being slightly reductionist, Software AES can be implemented in roughly two ways:
- The insecure but fast way.
- The slow but secure way.
Option 1 means using table look-ups, which are fast, but vulnerable to cache-timing attacks.
Option 2 means using a bitsliced implementation, like BearSSL provides.
Naturally, Proctorio’s AES Implementation Went For Option 1
You can find their AES implementation in the dhs.cipher.aes and w functions in J5HG.js.
What Is the Risk to Students?
Cache-timing vulnerabilities are much more dangerous to students than the previously disclosed issue with GMAC.
That is to say: They cough up your encryption keys. Furthermore, these only took 65 milliseconds to exploit (on 2006 hardware, to boot).
Cache-timing leaks can be easily exploited from other processes running on the same computer as Proctorio. This includes JavaScript code running in another browser window or tab.
Successfully exploiting this vulnerability would net you the keys used by Proctorio to encrypt and authenticate data, and exploiting it would not require violating any of the operating system’s security boundaries. Just running exploit code on the same hardware.
Isn’t cryptography fun?
https://soatok.blog/2020/09/12/edutech-spyware-is-still-spyware-proctorio-edition/
#AESGCM #cryptography #EduTech #JavaScript #Spyware #ZeroDay
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.This is because Grover’s quantum search algorithm can search
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Art by Swizz.However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called
This is often sold as an advantage: ReusingLet’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.If we assume AES is well-behaved, we can deduce that there are approximately
This is trivial to calculate. Simply divide the number of possible keys (
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
This means there are approximately
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection ofNote: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of
If you have a billion users (
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.
It’s tempting to think that a reuse of
However, it’s straightforward to go from a condition of
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- Use your knowledge of
- Calculate a new authentication tag for a chosen ciphertext using
While the blinding offered by XORing the final output with
Ergo, a collision in
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
As a user, you know that after
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM atThese limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography
As we look upon the sunset of a remarkably tiresome year, I thought it would be appropriate to talk about cryptographic wear-out.
What is cryptographic wear-out?
It’s the threshold when you’ve used the same key to encrypt so much data that you should probably switch to a new key before you encrypt any more. Otherwise, you might let someone capable of observing all your encrypted data perform interesting attacks that compromise the security of the data you’ve encrypted.
(Art by Swizz)
The exact value of the threshold varies depending on how exactly you’re encrypting data (n.b. AEAD modes, block ciphers + cipher modes, etc. each have different wear-out thresholds due to their composition).
Let’s take a look at the wear-out limits of the more popular symmetric encryption methods, and calculate those limits ourselves.
Specific Ciphers and Modes
Cryptographic Limits for AES-GCM
I’ve written about AES-GCM before (and why I think it sucks).
AES-GCM is a construction that combines AES-CTR with an authenticator called GMAC, whose consumption of nonces looks something like this:
- Calculating H (used in GHASH for all messages encrypted under the same key, regardless of nonce):
Encrypt(00000000 00000000 00000000 00000000)
- Calculating J0 (the pre-counter block):
- If the nonce is 96 bits long:
NNNNNNNN NNNNNNNN NNNNNNNN 00000001where theNspaces represent the nonce hexits.
- Otherwise:
s = 128 * ceil(len(nonce)/nonce) - len(nonce)
J0 = GHASH(H, nonce || zero(s+64) || int2bytes(len(nonce))
- If the nonce is 96 bits long:
- Each block of data encrypted uses J0 + block counter (starting at 1) as a CTR nonce.
- J0 is additionally used as the nonce to calculate the final GMAC tag.
AES-GCM is one of the algorithms where it’s easy to separately calculate the safety limits per message (i.e. for a given nonce and key), as well as for all messages under a key.
AES-GCM Single Message Length Limits
In the simplest case (nonce is 96 bits), you end up with the following nonces consumed:
- For each key:
00000000 00000000 00000000 00000000 - For each (nonce, key) pair:
NNNNNNNN NNNNNNNN NNNNNNNN 000000001for J0NNNNNNNN NNNNNNNN NNNNNNNN 000000002for encrypting the first 16 bytes of plaintextNNNNNNNN NNNNNNNN NNNNNNNN 000000003for the next 16 bytes of plaintext…- …
NNNNNNNN NNNNNNNN NNNNNNNN FFFFFFFFFfor the final 16 bytes of plaintext.
From here, it’s pretty easy to see that you can encrypt the blocks from 00000002 to FFFFFFFF without overflowing and creating a nonce reuse. This means that each (key, nonce) can be used to encrypt a single message up to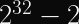 
Since the block size of AES is 16 bytes, this means the maximum length of a single AES-GCM (key, nonce) pair is 
Things get a bit tricker to analyze when the nonce is not 96 bits, since it’s hashed.
The disadvantage of this hashing behavior is that it’s possible for two different nonces to produce overlapping ranges of AES-CTR output, which makes the security analysis very difficult.
However, this hashed output is also hidden from network observers since they do not know the value of H. Without some method of reliably detecting when you have an overlapping range of hidden block counters, you can’t exploit this.
(If you want to live dangerously and motivate cryptanalysis research, mix 96-bit and non-96-bit nonces with the same key in a system that does something valuable.)
Multi-Message AES-GCM Key Wear-Out
Now that we’ve established the maximum length for a single message, how many messages you can safely encrypt under a given AES-GCM key depends entirely on how your nonce is selected.
If you have a reliable counter, which is guaranteed to never repeat, and start it at 0 you can theoretically encrypt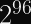 
(Art by Swizz)
You probably don’t have a reliable counter, especially in real-world settings (distributed systems, multi-threaded applications, virtual machines that might be snapshotted and restored, etc.).
(Art by Swizz)
Additionally (thanks to 2adic for the expedient correction), you cannot safely encrypt more than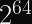 
Most systems that cannot guarantee unique incrementing nonces simply generate nonces with a cryptographically secure random number generator. This is a good idea, but no matter how high quality your random number generator is, random functions will produce collisions with a discrete probability.
If you have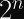 
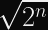
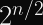
However, 50% of a nonce reuse isn’t exactly a comfortable safety threshold for most systems (especially since nonce reuse will cause AES-GCM to become vulnerable to active attackers). 1 in 4 billion is a much more comfortable safety margin against nonce reuse via collisions than 1 in 2. Fortunately, you can calculate the discrete probability of a birthday collision pretty easily.
If you want to rekey after your collision probability exceeds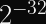 
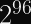
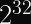
AES-GCM Safety Limits
- Maximum message length:
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
- Maximum data safely encrypted under a single key with a random nonce: about
bytes
(Art by Khia.)
Cryptographic Limits for ChaCha20-Poly1305
The IETF version of ChaCha20-Poly1305 uses 96-bit nonces and 32-bit internal counters. A similar analysis follows from AES-GCM’s, with a few notable exceptions.
For starters, the one-time Poly1305 key is derived from the first 32 bytes of the ChaCha20 keystream output (block 0) for a given (nonce, key) pair. There is no equivalent to AES-GCM’s H parameter which is static for each key. (The ChaCha20 encryption begins using block 1.)
Additionally, each block for ChaCha20 is 512 bits, unlike AES’s 128 bits. So the message limit here is a little more forgiving.
Since the block size is 512 bits (or 64 bytes), and only one block is consumed for Poly1305 key derivation, we can calculate a message length limit of 
The same rules for handling 96-bit nonces applies as with AES-GCM, so we can carry that value forward.
ChaCha20-Poly1305 Safety Limits
- Maximum message length:
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
- Maximum data safely encrypted under a single key with a random nonce: about
bytes
(Art by Khia.)
Cryptographic Limits for XChaCha20-Poly1305
XChaCha20-Poly1305 is a variant of XSalsa20-Poly1305 (as used in libsodium) and the IETF’s ChaCha20-Poly1305 construction. It features 192-bit nonces and 32-bit internal counters.
XChaCha20-Poly1305 is instantiated by using HChaCha20 of the key over the first 128 bits of the nonce to produce a subkey, which is used with the remaining nonce bits using the aforementioned ChaCha20-Poly1305.
This doesn’t change the maximum message length, but it does change the number of messages you can safely encrypt (since you’re actually using up to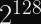 
Thus, even if you manage to repeat the final ChaCha20-Poly1305 nonce, as long as the total nonce differs, each encryptions will be performed with a distinct key (thanks to the HChaCha20 key derivation; see the XSalsa20 paper and IETF RFC draft for details).
UPDATE (2021-04-15): It turns out, my read of the libsodium implementation was erroneous due to endian-ness. The maximum message length for XChaCha20-Poly1305 is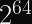 
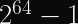
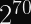
XChaCha20-Poly1305 Safety Limits
- Maximum message length:
- Maximum number of messages (random nonce):
- Maximum number of messages (sequential nonce):
(but you probably don’t have this luxury in the real world)
- Maximum data safely encrypted under a single key with a random nonce: about
bytes
see encrypt forever, man.
(Art by Khia.)
Cryptographic Limits for AES-CBC
It’s tempting to compare non-AEAD constructions and block cipher modes such as CBC (Cipher Block Chaining), but they’re totally different monsters.
- AEAD ciphers have a clean delineation between message length limit and the message quantity limit
- CBC and other cipher modes do not have this separation
Every time you encrypt a block with AES-CBC, you are depleting from a universal bucket that affects the birthday bound security of encrypting more messages under that key. (And unlike AES-GCM with long nonces, AES-CBC’s IV is public.)
This is in addition to the operational requirements of AES-CBC (plaintext padding, initialization vectors that never repeat and must be unpredictable, separate message authentication since CBC doesn’t provide integrity and is vulnerable to chosen-ciphertext atacks, etc.).
(Art by Khia.)
For this reason, most cryptographers don’t even bother calculating the safety limit for AES-CBC in the same breath as discussing AES-GCM. And they’re right to do so!
If you find yourself using AES-CBC (or AES-CTR, for that matter), you’d best be performing a separate HMAC-SHA256 over the ciphertext (and verifying this HMAC with a secure comparison function before decrypting). Additionally, you should consider using an extended nonce construction to split one-time encryption and authentication keys.
However, for the sake of completeness, let’s figure out what our practical limits are.
CBC operates on entire blocks of plaintext, whether you need the entire block or not.
On encryption, the output of the previous block is mixed (using XOR) with the current block, then encrypted with the block cipher. For the first block, the IV is used in the place of a “previous” block. (Hence, its requirements to be non-repeating and unpredictable.)
This means you can informally model (IV xor PlaintextBlock) and (PBn xor PBn+1) as a pseudo-random function, before it’s encrypted with the block cipher.
If those words don’t mean anything to you, here’s the kicker: You can use the above discussion about birthday bounds to calculate the upper safety bounds for the total number of blocks encrypted under a single AES key (assuming IVs are generated from a secure random source).
If you’re okay with a 50% probability of a collision, you should re-key after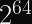
https://www.youtube.com/watch?v=v0IsYNDMV7A
If your safety margin is closer to the 1 in 4 billion (as with AES-GCM), you want to rekey after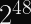 
However, blocks encrypted doesn’t map neatly to bytes encrypted.
If your plaintext is always an even multiple of 128 bits (or 16 bytes), this allows for up to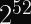 
On the other extreme (1-byte plaintexts), you’ll only be able to eek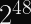
Therefore, to stay within the safety margin of AES-CBC, you SHOULD re-key after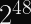
Keep in mind: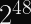 
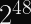
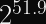
That’s Blocks. What About Bytes?
The actual plaintext byte limit sans padding is a bit fuzzy and context-dependent.
The local extrema occurs if your plaintext is always 16 bytes (and thus requires an extra 16 bytes of padding). Any less, and the padding fits within one block. Any more, and the data😛adding ratio starts to dominate.
Therefore, the worst case scenario with padding is that you take the above safety limit for block counts, and cut it in half. Cutting a number in half means reducing the exponent by 1.
But this still doesn’t eliminate the variance.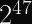 
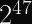
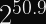
Therefore…
AES-CBC Safety Limits
- Maximum data safely encrypted under a single key with a random nonce:
(Art by Khia.)
Take-Away
Compared to AES-CBC, AES-GCM gives you approximately a million times as much usage out of the same key, for the same threat profile.
ChaCha20-Poly1305 and XChaCha20-Poly1305 provides even greater allowances of encrypting data under the same key. The latter is even safe to use to encrypt arbitrarily large volumes of data under a single key without having to worry about ever practically hitting the birthday bound.
I’m aware that this blog post could have simply been a comparison table and a few footnotes (or even an IETF RFC draft), but I thought it would be more fun to explain how these values are derived from the cipher constructions.
https://soatok.blog/2020/12/24/cryptographic-wear-out-for-symmetric-encryption/
#AES #AESCBC #AESGCM #birthdayAttack #birthdayBound #cryptography #safetyMargin #SecurityGuidance #symmetricCryptography #symmetricEncryption #wearOut
There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.Today, we’re going to look at how some symmetric encryption methods stack up against each other.
If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.
Comparisons
- AES-GCM vs. ChaCha20-Poly1305
- AES-GCM vs. XChaCha20-Poly1305
- AES-GCM vs. AES-CCM
- AES-GCM vs. AES-GCM-SIV
- AES-GCM vs. AES-SIV
- AES-GCM-SIV vs. AES-SIV
- AES-GCM vs. AES-CBC
- AES-GCM vs. AES-CTR
- AES-CBC vs. AES-CTR
- AES-CBC vs. AES-ECB
- AES vs. Blowfish
- ChaCha vs. Salsa20
- ChaCha vs. RC4
- Cipher Cascades
AES-GCM vs. ChaCha20-Poly1305
- If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
- Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
- AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
- Nonce size:
- AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
- ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).
- Wearout of a single (key, nonce) pair:
- AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
- ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).
- Neither algorithm is nonce misuse resistant.
Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.
AES-GCM vs. XChaCha20-Poly1305
- XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
- To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
- The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.
Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.
AES-GCM vs. AES-CCM
AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.
Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).
A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.
Conclusion: Just use AES-GCM.
AES-GCM vs. AES-GCM-SIV
AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.
The algorithms are significantly different:
- AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
- AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)
AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.
So really, use which ever you want.
Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?
https://twitter.com/colmmacc/status/986286693572493312
Conclusion: AES-GCM-SIV is better, but both are fine.
AES-GCM vs. AES-SIV
At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:
- Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
- AES-SIV is MAC then encrypt (so is AES-CCM).
- AES-SIV uses AES-CTR (so does AES-CCM).
If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.
AES-GCM also has the added advantage of not relying on CBC-MAC.
Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.
AES-GCM-SIV vs. AES-SIV
If you read the previous two sections, the conclusion here should be obvious.
- AES-GCM-SIV is slightly better than AES-GCM.
- AES-GCM is better than AES-SIV.
Conclusion: Use AES-GCM-SIV.
AES-GCM vs. AES-CBC
Just use AES-GCM. No contest.AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).
If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).
If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:
- encKey := HmacSha256(“encryption-cbc-hmac”, key)
- macKey := HmacSha256(“authentication-cbc-hmac”, key)
- iv := RandomBytes(16)
- ciphertext := AesCbc(plaintext, iv, encKey)
- tag := HmacSha256(iv + ciphertext, macKey)
For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.
There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.
AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.
AES-GCM vs. AES-CTR
Just use AES-GCM. No contest.Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.
If you must use AES-CTR, the same rules apply as for AES-CBC:
- encKey := HmacSha256(“encryption-ctr-hmac”, key)
- macKey := HmacSha256(“authentication-ctr-hmac”, key)
- nonce := RandomBytes(16)
- ciphertext := AesCtr(plaintext, nonce, encKey)
- tag := HmacSha256(nonce + ciphertext, macKey)
For decryption you need a secure compare function.
AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
AES-CBC vs. AES-CTR
If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.That being said:
AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.
AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.
If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.
AES-CBC vs. AES-ECB
Never use ECB mode. ECB mode lacks semantic security.Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.
Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.
AES vs. Blowfish
A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:
Why?! (Art by Khia)
Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”
Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.
AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.
AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.
Conclusion: Use AES instead of Blowfish.
ChaCha vs. Salsa20
Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.
Conclusion: Your choice (both are good but ChaCha is slightly better).
ChaCha vs. RC4
Don’t use RC4 for anything! What are you doing?
My reaction when I read that the CIA was using a modified RC4 in their Assassin malware instead of a secure stream cipher, per the Vault7 leaks. (Art by Khia)
RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.
Conclusion: Use ChaCha. Never use RC4.
Cipher Cascades
A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.
If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.
Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.
Symmetric Encryption Rankings
So with all of the above information, can we rank these algorithms into tiers?
Art by Riley
Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.
S XChaCha20-Poly1305, AES-GCM-SIV A AES-GCM, ChaCha20-Poly1305 B AES-SIV C AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2 D AES-CCM F Any: AES-ECB, RC4, Blowfish
Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaChaSoatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305
There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.
Today, we’re going to look at how some symmetric encryption methods stack up against each other.
If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.
Comparisons
- AES-GCM vs. ChaCha20-Poly1305
- AES-GCM vs. XChaCha20-Poly1305
- AES-GCM vs. AES-CCM
- AES-GCM vs. AES-GCM-SIV
- AES-GCM vs. AES-SIV
- AES-GCM-SIV vs. AES-SIV
- AES-GCM vs. AES-CBC
- AES-GCM vs. AES-CTR
- AES-CBC vs. AES-CTR
- AES-CBC vs. AES-ECB
- AES vs. Blowfish
- ChaCha vs. Salsa20
- ChaCha vs. RC4
- Cipher Cascades
AES-GCM vs. ChaCha20-Poly1305
- If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
- Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
- AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
- Nonce size:
- AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
- ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).
- Wearout of a single (key, nonce) pair:
- AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
- ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).
- Neither algorithm is nonce misuse resistant.
Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.
AES-GCM vs. XChaCha20-Poly1305
- XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
- To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
- The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.
Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.
AES-GCM vs. AES-CCM
AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.
Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.
Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).
A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.
Conclusion: Just use AES-GCM.
AES-GCM vs. AES-GCM-SIV
AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.
The algorithms are significantly different:
- AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
- AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)
AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.
So really, use which ever you want.
Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?
https://twitter.com/colmmacc/status/986286693572493312
Conclusion: AES-GCM-SIV is better, but both are fine.
AES-GCM vs. AES-SIV
At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:
- Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
- AES-SIV is MAC then encrypt (so is AES-CCM).
- AES-SIV uses AES-CTR (so does AES-CCM).
If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.
AES-GCM also has the added advantage of not relying on CBC-MAC.
Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.
AES-GCM-SIV vs. AES-SIV
If you read the previous two sections, the conclusion here should be obvious.
- AES-GCM-SIV is slightly better than AES-GCM.
- AES-GCM is better than AES-SIV.
Conclusion: Use AES-GCM-SIV.
AES-GCM vs. AES-CBC
Just use AES-GCM. No contest.
AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).
If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).
If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:
- encKey := HmacSha256(“encryption-cbc-hmac”, key)
- macKey := HmacSha256(“authentication-cbc-hmac”, key)
- iv := RandomBytes(16)
- ciphertext := AesCbc(plaintext, iv, encKey)
- tag := HmacSha256(iv + ciphertext, macKey)
For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.
There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.
AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.
AES-GCM vs. AES-CTR
Just use AES-GCM. No contest.
Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.
If you must use AES-CTR, the same rules apply as for AES-CBC:
- encKey := HmacSha256(“encryption-ctr-hmac”, key)
- macKey := HmacSha256(“authentication-ctr-hmac”, key)
- nonce := RandomBytes(16)
- ciphertext := AesCtr(plaintext, nonce, encKey)
- tag := HmacSha256(nonce + ciphertext, macKey)
For decryption you need a secure compare function.
AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
AES-CBC vs. AES-CTR
If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.
That being said:
AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.
AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.
If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.
AES-CBC vs. AES-ECB
Never use ECB mode. ECB mode lacks semantic security.
Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.
Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.
AES vs. Blowfish
A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:
Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”
Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.
AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.
AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.
Conclusion: Use AES instead of Blowfish.
ChaCha vs. Salsa20
Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.
That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.
Conclusion: Your choice (both are good but ChaCha is slightly better).
ChaCha vs. RC4
Don’t use RC4 for anything! What are you doing?
RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.
Conclusion: Use ChaCha. Never use RC4.
Cipher Cascades
A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).
Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.
If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.
Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.
Symmetric Encryption Rankings
So with all of the above information, can we rank these algorithms into tiers?
Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.
| S | XChaCha20-Poly1305, AES-GCM-SIV |
| A | AES-GCM, ChaCha20-Poly1305 |
| B | AES-SIV |
| C | AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2 |
| D | AES-CCM |
| F | Any: AES-ECB, RC4, Blowfish Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaCha |
Soatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/
#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305
Authenticated Key Exchanges are an interesting and important building block in any protocol that aims to allow people to communicate privately over an untrusted medium (i.e. the Internet).What’s an AKE?
At their core, Authenticated Key Exchanges (AKEs for short) combine two different classes of protocol.
- An authentication mechanism, such as a MAC or a digital signature.
- Key encapsulation, usually through some sort of Diffie-Hellman.
A simple example of an AKE is the modern TLS handshake, which uses digital signatures (X.509 certificates signed by certificate authorities) to sign ephemeral Elliptic Curve Diffie-Hellman (ECDH) public keys, which is then used to derive a shared secret to encrypt and authenticate network traffic.
I guess I should say “simple” with scare quotes. Cryptography is very much a “devil’s in the details” field, because my above explanation didn’t even encapsulate mutual-auth TLS or the underlying machinery of protocol negotiation. (Or the fact that non-forward-secret ciphersuites can be selected.)
AKEs get much more complicated, the more sophisticated your threat model becomes.
For example: Signal’s X3DH and Double Ratchet protocols are components of a very sophisticated AKE. Learn more about them here.
The IETF is working to standardize their own approach, called Messaging Layer Security (MLS), which uses a binary tree of ECDH handshakes to manage state and optimize group operations (called TreeKEM). You can learn more about IETF MLS here.
Password AKEs
Recently, a collection of cryptographers at the IETF’s Crypto Research Forum Group (CFRG) decided to hammer on a series of proposed Password-Authenticated Key Exchange (PAKE) protocols.PAKEs come in two flavors: Balanced (mutually authenticated) and augmented (one side is a prover, the other is a verifier). Balanced PAKEs are good for encrypted tunnels where you control both endpoints (e.g. WiFi networks), whereas Augmented PAKEs are great for eliminating the risk of password theft in client-server applications, if the server gets hacked.
Ultimately, the CFRG settled on one balanced PAKE (CPace) and one augmented PAKE (OPAQUE).
Consequently, cryptographer Filippo Valsorda managed to implement CPace in 125 lines of Go, using Ristretto255.
I implemented the CPace PAKE yesterday with Go and ristretto255, and it felt like cheating.125 lines of code! Really happy with it and it was a lot of fun.
— Filippo Valsorda (@FiloSottile) March 29, 2020
Why So Complicated?
At the end of the day, an AKE is just a construction that combines key encapsulation with an authentication mechanism.But how you combine these components together can vary wildly!
Some AKE designs (i.e. Dragonfly, in WPA3) are weaker than others; even if only in the sense of being difficult to implement in constant-time.
The reason there’s so many is that cryptographers tend to collectively decide which algorithms to recommend for standardization.
(n.b. There are a lot more block ciphers than DES, Blowfish, and AES to choose from! But ask a non-cryptographer to name five block ciphers and they’ll probably struggle.)
https://soatok.blog/2020/04/21/authenticated-key-exchanges/
#ake #authenticatedKeyExchange #cryptography #ECDH
If you’re reading this wondering if you should stop using AES-GCM in some standard protocol (TLS 1.3), the short answer is “No, you’re fine”.
I specialize in secure implementations of cryptography, and my years of experience in this field have led me to dislike AES-GCM.
This post is about why I dislike AES-GCM’s design, not “why AES-GCM is insecure and should be avoided”. AES-GCM is still miles above what most developers reach for when they want to encrypt (e.g. ECB mode or CBC mode). If you want a detailed comparison, read this.
To be clear: This is solely my opinion and not representative of any company or academic institution.
What is AES-GCM?
AES-GCM is an authenticated encryption mode that uses the AES block cipher in counter mode with a polynomial MAC based on Galois field multiplication.
In order to explain why AES-GCM sucks, I have to first explain what I dislike about the AES block cipher. Then, I can describe why I’m filled with sadness every time I see the AES-GCM construction used.
What is AES?
The Advanced Encryption Standard (AES) is a specific subset of a block cipher called Rijndael.
Rijndael’s design is based on a substitution-permutation network, which broke tradition from many block ciphers of its era (including its predecessor, DES) in not using a Feistel network.
AES only includes three flavors of Rijndael: AES-128, AES-192, and AES-256. The difference between these flavors is the size of the key and the number of rounds used, but–and this is often overlooked–not the block size.
As a block cipher, AES always operates on 128-bit (16 byte) blocks of plaintext, regardless of the key size.
This is generally considered acceptable because AES is a secure pseudorandom permutation (PRP), which means that every possible plaintext block maps directly to one ciphertext block, and thus birthday collisions are not possible. (A pseudorandom function (PRF), conversely, does have birthday bound problems.)
Why AES Sucks
Side-Channels
The biggest reason why AES sucks is that its design uses a lookup table (called an S-Box) indexed by secret data, which is inherently vulnerable to cache-timing attacks (PDF).
There are workarounds for this AES vulnerability, but they either require hardware acceleration (AES-NI) or a technique called bitslicing.
The short of it is: With AES, you’re either using hardware acceleration, or you have to choose between performance and security. You cannot get fast, constant-time AES without hardware support.
Block Size
AES-128 is considered by experts to have a security level of 128 bits.
Similarly, AES-192 gets certified at 192-bit security, and AES-256 gets 256-bit security.
However, the AES block size is only 128 bits!
That might not sound like a big deal, but it severely limits the constructions you can create out of AES.
Consider the case of AES-CBC, where the output of each block of encryption is combined with the next block of plaintext (using XOR). This is typically used with a random 128-bit block (called the initialization vector, or IV) for the first block.
This means you expect a collision after encrypting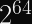
When you start getting collisions, you can break CBC mode, as this video demonstrates:
https://www.youtube.com/watch?v=v0IsYNDMV7A
This is significantly smaller than the
Post-Quantum Security?
With respect to the number of attempts needed to find the correct key, cryptographers estimate that AES-128 will have a post-quantum security level of 64 bits, AES-192 will have a post-quantum security level of 96 bits, and AES-256 will have a post-quantum security level of 128 bits.
This is because Grover’s quantum search algorithm can search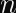
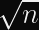
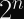
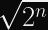
Note that this heuristic estimate is based on the number of guesses (a time factor), and doesn’t take circuit size into consideration. Grover’s algorithm also doesn’t parallelize well. The real-world security of AES may still be above 100 bits if you consider these nuances.
But remember, even AES-256 operates on 128-bit blocks.
Consequently, for AES-256, there should be approximately
Furthermore, there will be many keys that, for a constant plaintext block, will produce the same ciphertext block despite being a different key entirely. (n.b. This doesn’t mean for all plaintext/ciphertext block pairings, just some arbitrary pairing.)
Concrete example: Encrypting a plaintext block consisting of sixteen NUL bytes will yield a specific 128-bit ciphertext exactly once for each given AES-128 key. However, there are
This means it’s conceivable to accidentally construct a protocol that, despite using AES-256 safely, has a post-quantum security level on par with AES-128, which is only 64 bits.
This would not be nearly as much of a problem if AES’s block size was 256 bits.
Real-World Example: Signal
The Signal messaging app is the state-of-the-art for private communications. If you were previously using PGP and email, you should use Signal instead.
Signal aims to provide private communications (text messaging, voice calls) between two mobile devices, piggybacking on your pre-existing contacts list.
Part of their operational requirements is that they must be user-friendly and secure on a wide range of Android devices, stretching all the way back to Android 4.4.
The Signal Protocol uses AES-CBC + HMAC-SHA256 for message encryption. Each message is encrypted with a different AES key (due to the Double Ratchet), which limits the practical blast radius of a cache-timing attack and makes practical exploitation difficult (since you can’t effectively replay decryption in order to leak bits about the key).
Thus, Signal’s message encryption is still secure even in the presence of vulnerable AES implementations.
Art by Swizz.
However, the storage service in the Signal App uses AES-GCM, and this key has to be reused in order for the encrypted storage to operate.
This means, for older phones without dedicated hardware support for AES (i.e. low-priced phones from 2013, which Signal aims to support), the risk of cache-timing attacks is still present.
What this means is, a malicious app that can flush the CPU cache and measure timing with sufficient precision can siphon the AES-GCM key used by Signal to encrypt your storage without ever violating the security boundaries enforced by the Android operating system.
As a result of the security boundaries never being crossed, these kind of side-channel attacks would likely evade forensic analysis, and would therefore be of interest to the malware developers working for nation states.
Of course, if you’re on newer hardware (i.e. Qualcomm Snapdragon 835), you have hardware-accelerated AES available, so it’s probably a moot point.
Why AES-GCM Sucks Even More
AES-GCM is an authenticated encryption mode that also supports additional authenticated data. Cryptographers call these modes AEAD.
AEAD modes are more flexible than simple block ciphers. Generally, your encryption API accepts the following:
- The plaintext message.
- The encryption key.
- A nonce (
- Optional additional data which will be authenticated but not encrypted.
The output of an AEAD function is both the ciphertext and an authentication tag, which is necessary (along with the key and nonce, and optional additional data) to decrypt the plaintext.
Cryptographers almost universally recommend using AEAD modes for symmetric-key data encryption.
That being said, AES-GCM is possibly my least favorite AEAD, and I’ve got good reasons to dislike it beyond simply, “It uses AES”.
GHASH Brittleness
The way AES-GCM is initialized is stupid: You encrypt an all-zero block with your AES key (in ECB mode) and store it in a variable called 
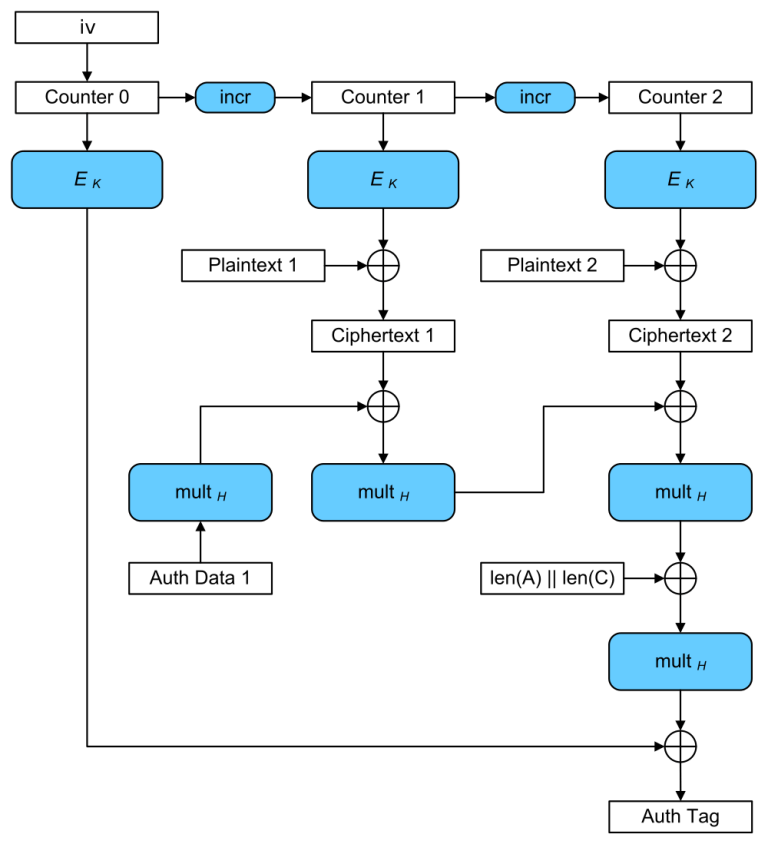
This is often sold as an advantage: Reusing
Let’s contrast AES-GCM with the other AEAD mode supported by TLS: ChaCha20-Poly1305, or ChaPoly for short.
ChaPoly uses one-time message authentication keys (derived from each key/nonce pair). If you manage to leak a Poly1305 key, the impact is limited to the messages encrypted under that (ChaCha20 key, nonce) pair.
While that’s still bad, it isn’t “decrypt all messages under that key forever” bad like with AES-GCM.
Note: “Message Authentication” here is symmetric, which only provides a property called message integrity, not sender authenticity. For the latter, you need asymmetric cryptography (wherein the ability to verify a message doesn’t imply the capability to generate a new signature), which is totally disparate from symmetric algorithms like AES or GHASH. You probably don’t need to care about this nuance right now, but it’s good to know in case you’re quizzed on it later.
H Reuse and Multi-User Security
If you recall, AES operates on 128-bit blocks even when 256-bit keys are used.
If we assume AES is well-behaved, we can deduce that there are approximately
This is trivial to calculate. Simply divide the number of possible keys (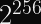
Each key that will map an arbitrarily specific plaintext block to a specific ciphertext block is also separated in the keyspace by approximately
This means there are approximately
“Why Does This Matter?”
It means that, with keys larger than 128 bits, you can model the selection of
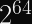
Note: Your 128-bit randomly generated AES keys already have this probability baked into their selection, but this specific analysis doesn’t really apply for 128-bit keys since AES is a PRP, not a PRF, so there is no “collision” risk. However, you end up at the same upper limit either way.
But 50% isn’t good enough for cryptographic security.
In most real-world systems, we target a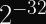
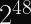
This isn’t the same thing as symmetric wear-out (where you need to re-key after a given number of encryptions to prevent nonce reuse). Rather, it means after your entire population has exhausted the safety limit of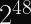
If you have a billion users (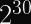
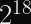
“What Good is H Reuse for Attackers if HF differs?”
There are two numbers used in AES-GCM that are derived from the AES key.
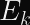
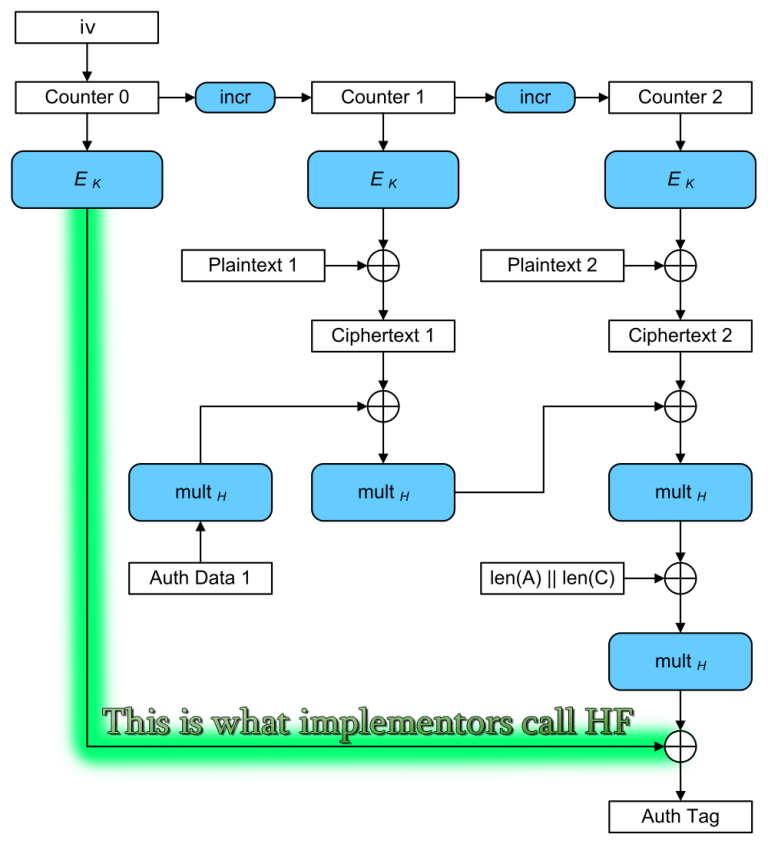
It’s tempting to think that a reuse of
However, it’s straightforward to go from a condition of
- Intercept multiple valid ciphertexts.
- e.g. Multiple JWTs encrypted with
{"alg":"A256GCM"}
- e.g. Multiple JWTs encrypted with
- Use your knowledge of
- Calculate a new authentication tag for a chosen ciphertext using
While the blinding offered by XORing the final output with
Ergo, a collision in
“How Could the Designers Have Prevented This?”
The core issue here is the AES block size, again.
If we were analyzing a 256-bit block variant of AES, and a congruent GCM construction built atop it, none of what I wrote in this section would apply.
However, the 128-bit block size was a design constraint enforced by NIST in the AES competition. This block size was during an era of 64-bit block ciphers (e.g. Triple-DES and Blowfish), so it was a significant improvement at the time.
NIST’s AES competition also inherited from the US government’s tradition of thinking in terms of “security levels”, which is why there are three different permitted key sizes (128, 192, or 256 bits).
“Why Isn’t This a Vulnerability?”
There’s always a significant gap in security, wherein something isn’t safe to recommend, but also isn’t susceptible to a known practical attack. This gap is important to keep systems secure, even when they aren’t on the bleeding edge of security.
Using 1024-bit RSA is a good example of this: No one has yet, to my knowledge, successfully factored a 1024-bit RSA public key. However, most systems have recommended a minimum 2048-bit for years (and many recommend 3072-bit or 4096-bit today).
With AES-GCM, the expected distance between collisions in
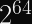
As a user, you know that after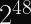
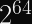
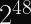
We don’t have that kind of distinguisher available to us today. And even if we had one available, the amount of data you need to search in order for any two users in the population to reuse/collide
Naturally, this isn’t a practical vulnerability. This is just another gripe I have with AES-GCM, as someone who has to work with cryptographic algorithms a lot.
Short Nonces
Although the AES block size is 16 bytes, AES-GCM nonces are only 12 bytes. The latter 4 bytes are dedicated to an internal counter, which is used with AES in Counter Mode to actually encrypt/decrypt messages.
(Yes, you can use arbitrary length nonces with AES-GCM, but if you use nonces longer than 12 bytes, they get hashed into 12 bytes anyway, so it’s not a detail most people should concern themselves with.)
If you ask a cryptographer, “How much can I encrypt safely with AES-GCM?” you’ll get two different answers.
- Message Length Limit: AES-GCM can be used to encrypt messages up to
- Number of Messages Limit: If you generate your nonces randomly, you have a 50% chance of a nonce collision after
However, 50% isn’t conservative enough for most systems, so the safety margin is usually much lower. Cryptographers generally set the key wear-out of AES-GCM at
These limits are acceptable for session keys for encryption-in-transit, but they impose serious operational limits on application-layer encryption with long-term keys.
Random Key Robustness
Before the advent of AEAD modes, cryptographers used to combine block cipher modes of operation (e.g. AES-CBC, AES-CTR) with a separate message authentication code algorithm (e.g. HMAC, CBC-MAC).
You had to be careful in how you composed your protocol, lest you invite Cryptographic Doom into your life. A lot of developers screwed this up. Standardized AEAD modes promised to make life easier.
Many developers gained their intuition for authenticated encryption modes from protocols like Signal’s (which combines AES-CBC with HMAC-SHA256), and would expect AES-GCM to be a drop-in replacement.
Unfortunately, GMAC doesn’t offer the same security benefits as HMAC: Finding a different (ciphertext, HMAC key) pair that produces the same authentication tag is a hard problem, due to HMAC’s reliance on cryptographic hash functions. This makes HMAC-based constructions “message committing”, which instills Random Key Robustness.
Critically, AES-GCM doesn’t have this property. You can calculate a random (ciphertext, key) pair that collides with a given authentication tag very easily.
This fact prohibits AES-GCM from being considered for use with OPAQUE (which requires RKR), one of the upcoming password-authenticated key exchange algorithms. (Read more about them here.)
Better-Designed Algorithms
You might be thinking, “Okay random furry, if you hate AES-GCM so much, what would you propose we use instead?”
XChaCha20-Poly1305
For encrypting messages under a long-term key, you can’t really beat XChaCha20-Poly1305.
- ChaCha is a stream cipher based on a 512-bit ARX hash function in counter mode. ChaCha doesn’t use S-Boxes. It’s fast and constant-time without hardware acceleration.
- ChaCha20 is ChaCha with 20 rounds.
- XChaCha nonces are 24 bytes, which allows you to generate them randomly and not worry about a birthday collision until about
- Poly1305 uses different 256-bit key for each (nonce, key) pair and is easier to implement in constant-time than AES-GCM.
- XChaCha20-Poly1305 uses the first 16 bytes of the nonce and the 256-bit key to generate a distinct subkey, and then employs the standard ChaCha20-Poly1305 construction used in TLS today.
For application-layer cryptography, XChaCha20-Poly1305 contains most of the properties you’d want from an authenticated mode.
However, like AES-GCM (and all other Polynomial MACs I’ve heard of), it is not message committing.
The Gimli Permutation
For lightweight cryptography (n.b. important for IoT), the Gimli permutation (e.g. employed in libhydrogen) is an attractive option.
Gimli is a Round 2 candidate in NIST’s Lightweight Cryptography project. The Gimli permutation offers a lot of applications: a hash function, message authentication, encryption, etc.
Critically, it’s possible to construct a message-committing protocol out of Gimli that will hit a lot of the performance goals important to embedded systems.
Closing Remarks
Despite my personal disdain for AES-GCM, if you’re using it as intended by cryptographers, it’s good enough.
Don’t throw AES-GCM out just because of my opinions. It’s very likely the best option you have.
Although I personally dislike AES and GCM, I’m still deeply appreciative of the brilliance and ingenuity that went into both designs.
My desire is for the industry to improve upon AES and GCM in future cipher designs so we can protect more people, from a wider range of threats, in more diverse protocols, at a cheaper CPU/memory/time cost.
We wouldn’t have a secure modern Internet without the work of Vincent Rijmen, Joan Daemen, John Viega, David A. McGrew, and the countless other cryptographers and security researchers who made AES-GCM possible.
Change Log
- 2021-10-26: Added section on H Reuse and Multi-User Security.
https://soatok.blog/2020/05/13/why-aes-gcm-sucks/
#AES #AESGCM #cryptography #GaloisCounterMode #opinion #SecurityGuidance #symmetricCryptography
There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.Today, we’re going to look at how some symmetric encryption methods stack up against each other.
If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.
Comparisons
- AES-GCM vs. ChaCha20-Poly1305
- AES-GCM vs. XChaCha20-Poly1305
- AES-GCM vs. AES-CCM
- AES-GCM vs. AES-GCM-SIV
- AES-GCM vs. AES-SIV
- AES-GCM-SIV vs. AES-SIV
- AES-GCM vs. AES-CBC
- AES-GCM vs. AES-CTR
- AES-CBC vs. AES-CTR
- AES-CBC vs. AES-ECB
- AES vs. Blowfish
- ChaCha vs. Salsa20
- ChaCha vs. RC4
- Cipher Cascades
AES-GCM vs. ChaCha20-Poly1305
- If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
- Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
- AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
- Nonce size:
- AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
- ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).
- Wearout of a single (key, nonce) pair:
- AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
- ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).
- Neither algorithm is nonce misuse resistant.
Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.
AES-GCM vs. XChaCha20-Poly1305
- XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
- To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
- The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.
Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.
AES-GCM vs. AES-CCM
AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.
Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).
A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.
Conclusion: Just use AES-GCM.
AES-GCM vs. AES-GCM-SIV
AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.
The algorithms are significantly different:
- AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
- AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)
AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.
So really, use which ever you want.
Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?
https://twitter.com/colmmacc/status/986286693572493312
Conclusion: AES-GCM-SIV is better, but both are fine.
AES-GCM vs. AES-SIV
At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:
- Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
- AES-SIV is MAC then encrypt (so is AES-CCM).
- AES-SIV uses AES-CTR (so does AES-CCM).
If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.
AES-GCM also has the added advantage of not relying on CBC-MAC.
Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.
AES-GCM-SIV vs. AES-SIV
If you read the previous two sections, the conclusion here should be obvious.
- AES-GCM-SIV is slightly better than AES-GCM.
- AES-GCM is better than AES-SIV.
Conclusion: Use AES-GCM-SIV.
AES-GCM vs. AES-CBC
Just use AES-GCM. No contest.AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).
If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).
If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:
- encKey := HmacSha256(“encryption-cbc-hmac”, key)
- macKey := HmacSha256(“authentication-cbc-hmac”, key)
- iv := RandomBytes(16)
- ciphertext := AesCbc(plaintext, iv, encKey)
- tag := HmacSha256(iv + ciphertext, macKey)
For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.
There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.
AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.
AES-GCM vs. AES-CTR
Just use AES-GCM. No contest.Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.
If you must use AES-CTR, the same rules apply as for AES-CBC:
- encKey := HmacSha256(“encryption-ctr-hmac”, key)
- macKey := HmacSha256(“authentication-ctr-hmac”, key)
- nonce := RandomBytes(16)
- ciphertext := AesCtr(plaintext, nonce, encKey)
- tag := HmacSha256(nonce + ciphertext, macKey)
For decryption you need a secure compare function.
AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.
AES-CBC vs. AES-CTR
If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.That being said:
AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.
AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.
If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.
AES-CBC vs. AES-ECB
Never use ECB mode. ECB mode lacks semantic security.Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.
Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.
AES vs. Blowfish
A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:
Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”
Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.
AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.
AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.
Conclusion: Use AES instead of Blowfish.
ChaCha vs. Salsa20
Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.
Conclusion: Your choice (both are good but ChaCha is slightly better).
ChaCha vs. RC4
Don’t use RC4 for anything! What are you doing?
RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.
Conclusion: Use ChaCha. Never use RC4.
Cipher Cascades
A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.
If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.
Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.
Symmetric Encryption Rankings
So with all of the above information, can we rank these algorithms into tiers?
Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.
S XChaCha20-Poly1305, AES-GCM-SIV A AES-GCM, ChaCha20-Poly1305 B AES-SIV C AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2 D AES-CCM F Any: AES-ECB, RC4, Blowfish
Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaChaSoatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305
