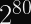As we look upon the sunset of a remarkably tiresome year, I thought it would be appropriate to talk about cryptographic wear-out.

What is cryptographic wear-out?

It’s the threshold when you’ve used the same key to encrypt so much data that you should probably switch to a new key before you encrypt any more. Otherwise, you might let someone capable of observing all your encrypted data perform interesting attacks that compromise the security of the data you’ve encrypted.

My definitions always aim to be more understandable than pedantically correct.
(Art by Swizz)

The exact value of the threshold varies depending on how exactly you’re encrypting data (n.b. AEAD modes, block ciphers + cipher modes, etc. each have different wear-out thresholds due to their composition).

Let’s take a look at the wear-out limits of the more popular symmetric encryption methods, and calculate those limits ourselves.

Specific Ciphers and Modes

(Art by Khia. Poorly edited by the author.)

Cryptographic Limits for AES-GCM

I’ve written about AES-GCM before (and why I think it sucks).

AES-GCM is a construction that combines AES-CTR with an authenticator called GMAC, whose consumption of nonces looks something like this:

• Calculating H (used in GHASH for all messages encrypted under the same key, regardless of nonce):
  
  • Encrypt(00000000 00000000 00000000 00000000)

  
  

• Calculating J0 (the pre-counter block):
  
  • If the nonce is 96 bits long:
    
    • NNNNNNNN NNNNNNNN NNNNNNNN 00000001 where the N spaces represent the nonce hexits.

    
    

  • Otherwise:
    
    • s = 128 * ceil(len(nonce)/nonce) - len(nonce)
    • J0 = GHASH(H, nonce || zero(s+64) || int2bytes(len(nonce))

    
    

  
  

• Each block of data encrypted uses J0 + block counter (starting at 1) as a CTR nonce.
• J0 is additionally used as the nonce to calculate the final GMAC tag.

AES-GCM is one of the algorithms where it’s easy to separately calculate the safety limits per message (i.e. for a given nonce and key), as well as for all messages under a key.

AES-GCM Single Message Length Limits

In the simplest case (nonce is 96 bits), you end up with the following nonces consumed:

• For each key: 00000000 00000000 00000000 00000000
• For each (nonce, key) pair:
  
  • NNNNNNNN NNNNNNNN NNNNNNNN 000000001 for J0
  • NNNNNNNN NNNNNNNN NNNNNNNN 000000002 for encrypting the first 16 bytes of plaintext
  • NNNNNNNN NNNNNNNN NNNNNNNN 000000003 for the next 16 bytes of plaintext…
  • …
  • NNNNNNNN NNNNNNNN NNNNNNNN FFFFFFFFF for the final 16 bytes of plaintext.

  
  

From here, it’s pretty easy to see that you can encrypt the blocks from 00000002 to FFFFFFFF without overflowing and creating a nonce reuse. This means that each (key, nonce) can be used to encrypt a single message up to 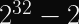blocks of the underlying ciphertext.

Since the block size of AES is 16 bytes, this means the maximum length of a single AES-GCM (key, nonce) pair is bytes (or 68,719,476,480 bytes). This is approximately 68 GB or 64 GiB.

Things get a bit tricker to analyze when the nonce is not 96 bits, since it’s hashed.

The disadvantage of this hashing behavior is that it’s possible for two different nonces to produce overlapping ranges of AES-CTR output, which makes the security analysis very difficult.

However, this hashed output is also hidden from network observers since they do not know the value of H. Without some method of reliably detecting when you have an overlapping range of hidden block counters, you can’t exploit this.

(If you want to live dangerously and motivate cryptanalysis research, mix 96-bit and non-96-bit nonces with the same key in a system that does something valuable.)

Multi-Message AES-GCM Key Wear-Out

Now that we’ve established the maximum length for a single message, how many messages you can safely encrypt under a given AES-GCM key depends entirely on how your nonce is selected.

If you have a reliable counter, which is guaranteed to never repeat, and start it at 0 you can theoretically encrypt messages safely. Hooray!

Hooray!
(Art by Swizz)

You probably don’t have a reliable counter, especially in real-world settings (distributed systems, multi-threaded applications, virtual machines that might be snapshotted and restored, etc.).

Confound you, technical limitations!
(Art by Swizz)

Additionally (thanks to 2adic for the expedient correction), you cannot safely encrypt more than blocks with AES because the keystream blocks–as the output of a block cipher–cannot repeat.

Most systems that cannot guarantee unique incrementing nonces simply generate nonces with a cryptographically secure random number generator. This is a good idea, but no matter how high quality your random number generator is, random functions will produce collisions with a discrete probability.

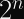
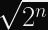
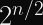
If you have possible values, you should expect a single collision(with 50% probability) after (or )samples. This is called the birthday bound.

However, 50% of a nonce reuse isn’t exactly a comfortable safety threshold for most systems (especially since nonce reuse will cause AES-GCM to become vulnerable to active attackers). 1 in 4 billion is a much more comfortable safety margin against nonce reuse via collisions than 1 in 2. Fortunately, you can calculate the discrete probability of a birthday collision pretty easily.

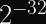
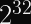
If you want to rekey after your collision probability exceeds (for a random nonce between 0 and ), you simply need to re-key after messages.

AES-GCM Safety Limits

• Maximum message length: bytes
• Maximum number of messages (random nonce):
• Maximum number of messages (sequential nonce): (but you probably don’t have this luxury in the real world)
• Maximum data safely encrypted under a single key with a random nonce: about bytes

Not bad, but we can do better.
(Art by Khia.)

Cryptographic Limits for ChaCha20-Poly1305

The IETF version of ChaCha20-Poly1305 uses 96-bit nonces and 32-bit internal counters. A similar analysis follows from AES-GCM’s, with a few notable exceptions.

For starters, the one-time Poly1305 key is derived from the first 32 bytes of the ChaCha20 keystream output (block 0) for a given (nonce, key) pair. There is no equivalent to AES-GCM’s H parameter which is static for each key. (The ChaCha20 encryption begins using block 1.)

Additionally, each block for ChaCha20 is 512 bits, unlike AES’s 128 bits. So the message limit here is a little more forgiving.

Since the block size is 512 bits (or 64 bytes), and only one block is consumed for Poly1305 key derivation, we can calculate a message length limit of , or 274,877,906,880 bytes–nearly 256 GiB for each (nonce, key) pair.

The same rules for handling 96-bit nonces applies as with AES-GCM, so we can carry that value forward.

ChaCha20-Poly1305 Safety Limits

• Maximum message length: bytes
• Maximum number of messages (random nonce):
• Maximum number of messages (sequential nonce): (but you probably don’t have this luxury in the real world)
• Maximum data safely encrypted under a single key with a random nonce: about bytes

A significant improvement, but still practically limited.
(Art by Khia.)

Cryptographic Limits for XChaCha20-Poly1305

XChaCha20-Poly1305 is a variant of XSalsa20-Poly1305 (as used in libsodium) and the IETF’s ChaCha20-Poly1305 construction. It features 192-bit nonces and 32-bit internal counters.

XChaCha20-Poly1305 is instantiated by using HChaCha20 of the key over the first 128 bits of the nonce to produce a subkey, which is used with the remaining nonce bits using the aforementioned ChaCha20-Poly1305.

This doesn’t change the maximum message length, but it does change the number of messages you can safely encrypt (since you’re actually using up to 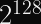distinct keys).

Thus, even if you manage to repeat the final ChaCha20-Poly1305 nonce, as long as the total nonce differs, each encryptions will be performed with a distinct key (thanks to the HChaCha20 key derivation; see the XSalsa20 paper and IETF RFC draft for details).

UPDATE (2021-04-15): It turns out, my read of the libsodium implementation was erroneous due to endian-ness. The maximum message length for XChaCha20-Poly1305 is blocks, and for AEAD_XChaCha20_Poly1305 is blocks. Each block is 64 bytes, so that changes the maximum message length to about . This doesn’t change the extended-nonce details, just the underlying ChaCha usage.

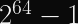
XChaCha20-Poly1305 Safety Limits

• Maximum message length: bytes (earlier version of this document said )
• Maximum number of messages (random nonce):
• Maximum number of messages (sequential nonce): (but you probably don’t have this luxury in the real world)
• Maximum data safely encrypted under a single key with a random nonce: about bytes

I can see encrypt forever, man.
(Art by Khia.)

Cryptographic Limits for AES-CBC

It’s tempting to compare non-AEAD constructions and block cipher modes such as CBC (Cipher Block Chaining), but they’re totally different monsters.

• AEAD ciphers have a clean delineation between message length limit and the message quantity limit
• CBC and other cipher modes do not have this separation

Every time you encrypt a block with AES-CBC, you are depleting from a universal bucket that affects the birthday bound security of encrypting more messages under that key. (And unlike AES-GCM with long nonces, AES-CBC’s IV is public.)

This is in addition to the operational requirements of AES-CBC (plaintext padding, initialization vectors that never repeat and must be unpredictable, separate message authentication since CBC doesn’t provide integrity and is vulnerable to chosen-ciphertext atacks, etc.).

My canned response to most queries about AES-CBC.
(Art by Khia.)

For this reason, most cryptographers don’t even bother calculating the safety limit for AES-CBC in the same breath as discussing AES-GCM. And they’re right to do so!

If you find yourself using AES-CBC (or AES-CTR, for that matter), you’d best be performing a separate HMAC-SHA256 over the ciphertext (and verifying this HMAC with a secure comparison function before decrypting). Additionally, you should consider using an extended nonce construction to split one-time encryption and authentication keys.

(Art by Riley.)

However, for the sake of completeness, let’s figure out what our practical limits are.

CBC operates on entire blocks of plaintext, whether you need the entire block or not.

On encryption, the output of the previous block is mixed (using XOR) with the current block, then encrypted with the block cipher. For the first block, the IV is used in the place of a “previous” block. (Hence, its requirements to be non-repeating and unpredictable.)

This means you can informally model (IV xor PlaintextBlock) and (PBn xor PBn+1) as a pseudo-random function, before it’s encrypted with the block cipher.

If those words don’t mean anything to you, here’s the kicker: You can use the above discussion about birthday bounds to calculate the upper safety bounds for the total number of blocks encrypted under a single AES key (assuming IVs are generated from a secure random source).

If you’re okay with a 50% probability of a collision, you should re-key after blocks have been encrypted.

https://www.youtube.com/watch?v=v0IsYNDMV7A

If your safety margin is closer to the 1 in 4 billion (as with AES-GCM), you want to rekey after blocks.

However, blocks encrypted doesn’t map neatly to bytes encrypted.

If your plaintext is always an even multiple of 128 bits (or 16 bytes), this allows for up to bytes of plaintext. If you’re using PKCS#7 padding, keep in mind that this will include an entire padding block per message, so your safety margin will deplete a bit faster (depending on how many individual messages you encrypt, and therefore how many padding blocks you need).

On the other extreme (1-byte plaintexts), you’ll only be able to eek encrypted bytes before you should re-key.

Therefore, to stay within the safety margin of AES-CBC, you SHOULD re-key after blocks (including padding) have been encrypted.

Keep in mind: single-byte blocks is still approximately 281 TiB of data (including padding). On the upper end, 15-byte blocks (with 1-byte padding to stay within a block) clocks in at about or about 4.22 PiB of data.

That’s Blocks. What About Bytes?

The actual plaintext byte limit sans padding is a bit fuzzy and context-dependent.

The local extrema occurs if your plaintext is always 16 bytes (and thus requires an extra 16 bytes of padding). Any less, and the padding fits within one block. Any more, and the data😛adding ratio starts to dominate.

Therefore, the worst case scenario with padding is that you take the above safety limit for block counts, and cut it in half. Cutting a number in half means reducing the exponent by 1.

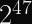
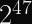
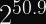
But this still doesn’t eliminate the variance. blocks could be anywhere from to bytes of real plaintext. When in situations like this, we have to assume the worst (n.b. take the most conservative value).

Therefore…

AES-CBC Safety Limits

• Maximum data safely encrypted under a single key with a random nonce: bytes (approximately 141 TiB)

Yet another reason to dislike non-AEAD ciphers.
(Art by Khia.)

Take-Away

Compared to AES-CBC, AES-GCM gives you approximately a million times as much usage out of the same key, for the same threat profile.

ChaCha20-Poly1305 and XChaCha20-Poly1305 provides even greater allowances of encrypting data under the same key. The latter is even safe to use to encrypt arbitrarily large volumes of data under a single key without having to worry about ever practically hitting the birthday bound.

I’m aware that this blog post could have simply been a comparison table and a few footnotes (or even an IETF RFC draft), but I thought it would be more fun to explain how these values are derived from the cipher constructions.

(Art by Khia.)

https://soatok.blog/2020/12/24/cryptographic-wear-out-for-symmetric-encryption/

#AES #AESCBC #AESGCM #birthdayAttack #birthdayBound #cryptography #safetyMargin #SecurityGuidance #symmetricCryptography #symmetricEncryption #wearOut

Dhole Moments

2020-07-12 21:33:27

There seems to be a lot of interest among software developers in the various cryptographic building blocks (block ciphers, hash functions, etc.), and more specifically how they stack up against each other.

Today, we’re going to look at how some symmetric encryption methods stack up against each other.

If you’re just looking for a short list of cryptographic “right answers”, your cheat sheet can be found on Latacora’s blog.

Comparisons

• AES-GCM vs. ChaCha20-Poly1305
• AES-GCM vs. XChaCha20-Poly1305
• AES-GCM vs. AES-CCM
• AES-GCM vs. AES-GCM-SIV
• AES-GCM vs. AES-SIV
• AES-GCM-SIV vs. AES-SIV
• AES-GCM vs. AES-CBC
• AES-GCM vs. AES-CTR
• AES-CBC vs. AES-CTR
• AES-CBC vs. AES-ECB
• AES vs. Blowfish
• ChaCha vs. Salsa20
• ChaCha vs. RC4
• Cipher Cascades

AES-GCM vs. ChaCha20-Poly1305

• If you have hardware acceleration (e.g. AES-NI), then AES-GCM provides better performance. If you do not, AES-GCM is either slower than ChaCha20-Poly1305, or it leaks your encryption keys in cache timing.
• Neither algorithm is message committing, which makes both unsuitable for algorithms like OPAQUE (explanation).
• AES-GCM can target multiple security levels (128-bit, 192-bit, 256-bit), whereas ChaCha20-Poly1305 is only defined at the 256-bit security level.
• Nonce size:
  
  • AES-GCM: Varies, but standard is 96 bits (12 bytes). If you supply a longer nonce, this gets hashed down to 16 bytes.
  • ChaCha20-Poly1305: The standardized version uses 96-bit nonces (12 bytes), but the original used 64-bit nonces (8 bytes).

  
  

• Wearout of a single (key, nonce) pair:
  
  • AES-GCM: Messages must be less than 2^32 – 2 blocks (a.k.a. 2^36 – 32 bytes, a.k.a. 2^39 – 256 bits). This also makes the security analysis of AES-GCM with long nonces complicated, since the hashed nonce doesn’t start with the lower 4 bytes set to 00 00 00 02.
  • ChaCha20-Poly1305: ChaCha has an internal counter (32 bits in the standardized IETF variant, 64 bits in the original design).

  
  

• Neither algorithm is nonce misuse resistant.

Conclusion: Both are good options. AES-GCM can be faster with hardware support, but pure-software implementations of ChaCha20-Poly1305 are almost always fast and constant-time.

Back to the top

AES-GCM vs. XChaCha20-Poly1305

• XChaCha20 accepts 192-bit nonces (24 bytes). The first 16 of the nonce are used with the ChaCha key to derive a subkey, and then the rest of this algorithm is the same as ChaCha20-Poly1305.
• To compare AES-GCM and ChaCha20-Poly1305 for encryption, see above.
• The longer nonce makes XChaCha20-Poly1305 better suited for long-lived keys (i.e. application-layer cryptography) than AES-GCM.

Conclusion: If you’re using the same key for a large number of messages, XChaCha20-Poly1305 has a wider safety margin than AES-GCM. Therefore, XChaCha20-Poly1305 should be preferred in those cases.

Back to the top

AES-GCM vs. AES-CCM

AES-GCM is AES in Galois/Counter Mode, AES-CCM is AES in Counter with CBC-MAC mode.

Although I previously stated that AES-GCM is possibly my least favorite AEAD, AES-CCM is decidedly worse: AES-GCM is Encrypt-then-MAC, while AES-CCM is MAC-then-encrypt.

Sure, CCM mode has a security proof that arguably justifies violating the cryptographic doom principle, but I contend the only time it’s worthwhile to do that is when you’re building a nonce-misuse resistant mode (i.e. AES-GCM-SIV).

A lot of cryptography libraries simply don’t even implement AES-CCM; or if they do, it’s disabled by default (i.e. OpenSSL). A notable exception is the Stanford Javascript Cryptography Library, which defaults to AES-CCM + PBKDF2 for encryption.

Conclusion: Just use AES-GCM.

Back to the top

AES-GCM vs. AES-GCM-SIV

AES-GCM-SIV encryption runs at 70% the speed of AES-GCM, but decryption is just as fast. What does this 30% encryption slowdown buy? Nonce misuse resistance.

Nonce misuse resistance is really cool. (Art by Swizz)

The algorithms are significantly different:

• AES-GCM is basically AES-CTR, then GMAC (parameterized by the key and nonce) is applied over the AAD and ciphertext. (Encrypt then MAC)
• AES-GCM-SIV derives two distinct keys from the nonce and key, then uses POLYVAL (which is related to GHASH) over the AAD and message with the first key to generate the tag. Then the tag used to derive a series of AES inputs that, when encrypted with the second key, are XORed with the blocks of the message (basically counter mode). (MAC then Encrypt)

AES-GCM is a simpler algorithm to analyze. AES-GCM-SIV provides a greater safety margin. However, like AES-GCM, AES-GCM-SIV is also vulnerable to the Invisible Salamanders attack.

So really, use which ever you want.

Better security comes from AES-GCM-SIV, better encryption performance comes from AES-GCM. What are your priorities?

https://twitter.com/colmmacc/status/986286693572493312

Conclusion: AES-GCM-SIV is better, but both are fine.

Back to the top

AES-GCM vs. AES-SIV

At the risk of being overly reductionist, AES-SIV is basically a nonce misuse resistant variant of AES-CCM:

• Where AES-CCM uses CBC-MAC, AES-SIV uses CMAC, which is based on CBC-MAC but with a doubling step (left shift then XOR with the round constant).
• AES-SIV is MAC then encrypt (so is AES-CCM).
• AES-SIV uses AES-CTR (so does AES-CCM).

If you need nonce misuse resistance, AES-SIV is a tempting choice, but you’re going to get better performance out of AES-GCM.

AES-GCM also has the added advantage of not relying on CBC-MAC.

Conclusion: Prefer AES-GCM in most threat models, AES-SIV in narrower threat models where nonce misuse is the foremost security risk.

Back to the top

AES-GCM-SIV vs. AES-SIV

If you read the previous two sections, the conclusion here should be obvious.

• AES-GCM-SIV is slightly better than AES-GCM.
• AES-GCM is better than AES-SIV.

Conclusion: Use AES-GCM-SIV.

Back to the top

AES-GCM vs. AES-CBC

Just use AES-GCM. No contest.

AES-GCM is an authenticated encryption mode. It doesn’t just provide confidentiality by encrypting your message, it also provides integrity (which guarantees that nobody tampered with the encrypted message over the wire).

If you select AES-CBC instead of AES-GCM, you’re opening your systems to a type of attack called a padding oracle (which lets attackers decrypt messages without the key, by replaying altered ciphertexts and studying the behavior of your application).

If you must use AES-CBC, then you must also MAC your ciphertext (and the initialization vector–IV for short). You should also devise some sort of key-separation mechanism so you’re not using the same key for two different algorithms. Even something like this is fine:

1. encKey := HmacSha256(“encryption-cbc-hmac”, key)
2. macKey := HmacSha256(“authentication-cbc-hmac”, key)
3. iv := RandomBytes(16)
4. ciphertext := AesCbc(plaintext, iv, encKey)
5. tag := HmacSha256(iv + ciphertext, macKey)

For decryption you need a secure compare function. If one is not available to you, or you cannot guarantee it will run in constant time, a second HMAC call with a random per-comparison key will suffice.

There is no possible world in which case unauthenticated AES-CBC is a safer choice than AES-GCM.

AES-CBC + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.

The Signal Protocol uses AES-CBC + HMAC-SHA2 for message encryption.

Back to the top

AES-GCM vs. AES-CTR

Just use AES-GCM. No contest.

Unlike AES-GCM, AES-CTR doesn’t provide any message integrity guarantees. However, strictly speaking, AES-GCM uses AES-CTR under the hood.

If you must use AES-CTR, the same rules apply as for AES-CBC:

1. encKey := HmacSha256(“encryption-ctr-hmac”, key)
2. macKey := HmacSha256(“authentication-ctr-hmac”, key)
3. nonce := RandomBytes(16)
4. ciphertext := AesCtr(plaintext, nonce, encKey)
5. tag := HmacSha256(nonce + ciphertext, macKey)

For decryption you need a secure compare function.

AES-CTR + HMAC-SHA256 (encrypt then MAC) is message-committing and therefore can be safely used with algorithms like OPAQUE.

Back to the top

AES-CBC vs. AES-CTR

If you find yourself trying to decide between CBC mode and CTR mode, you should probably save yourself the headache and just use GCM instead.

That being said:

AES-CTR fails harder than AES-CBC when you reuse an IV/nonce.

AES-CBC requires a padding scheme (e.g. PKCS #7 padding) which adds unnecessary algorithmic complexity.

If you have to decide between the two, and you have a robust extended-nonce key-splitting scheme in place, opt for AES-CTR. But really, unless you’re a cryptography engineer well-versed in the nuances and failure modes of these algorithms, you shouldn’t even be making this choice.

Back to the top

AES-CBC vs. AES-ECB

Never use ECB mode. ECB mode lacks semantic security.

Block cipher modes that support initialization vectors were invented to compensate for this shortcoming.

Conclusion: If you’re trying to decide between these two, you’ve already lost. Rethink your strategy.

Back to the top

AES vs. Blowfish

A lot of OpenVPN configurations in the wild default to Blowfish for encryption. To the authors of these configuration files, I have but one question:

Why?! (Art by Khia)

Sure, you might think, “But Blowfish supports up to 448-bit keys and is therefore more secure than even 256-bit AES.”

Cryptographic security isn’t a dick-measuring contest. Key size isn’t everything. More key isn’t more security.

AES is a block cipher with a 128-bit block size. Blowfish is a block cipher with a 64-bit block size. This means that Blowfish in CBC mode is vulnerable to birthday attacks in a practical setting.

AES has received several orders of magnitude more scrutiny from cryptography experts than Blowfish has.

Conclusion: Use AES instead of Blowfish.

Back to the top

ChaCha vs. Salsa20

Salsa20 is an eSTREAM finalist stream cipher. After years of cryptanalysis, reduced round variants of Salsa20 (specifically, Salsa20/7 with a 128-bit key) were found to be breakable. In response to this, a variant called ChaCha was published that increased the per-round diffusion.

That is to say: ChaCha is generally more secure than Salsa20 with similar or slightly better performance. If you have to choose between the two, go for ChaCha.

Conclusion: Your choice (both are good but ChaCha is slightly better).

Back to the top

ChaCha vs. RC4

Don’t use RC4 for anything! What are you doing?

My reaction when I read that the CIA was using a modified RC4 in their Assassin malware instead of a secure stream cipher, per the Vault7 leaks. (Art by Khia)

RC4 was a stream cipher–allegedly designed by Ron Rivest and leaked onto a mailing list–that has been thoroughly demolished by cryptanalysis. RC4 is not secure and should never be relied on for security.

Conclusion: Use ChaCha. Never use RC4.

Back to the top

Cipher Cascades

A cipher cascade is when you encrypt a message with one cipher, and then encrypt the ciphertext with another cipher, sometimes multiple times. One example: TripleSec by Keybase, which combines AES and Salsa20 (and, formerly, Twofish–an AES finalist).

Cipher cascades don’t meaningfully improve security in realistic threat models. However, if your threat model includes “AES is broken or backdoored by the NSA”, a cipher cascade using AES is safer than just selecting a nonstandard cipher instead of AES. However, they’re necessarily slower than just using AES would be.

If you’re worried about this, your time is better spent worrying about key management, side-channel attacks, and software supply chain attacks.

Conclusion: Avoid cipher cascades, but they’re better than recklessly paranoid alternatives.

Back to the top

Symmetric Encryption Rankings

So with all of the above information, can we rank these algorithms into tiers?

Art by Riley

Sort of! Although it’s based on the above analyses, ranking is inherently subjective. So what follows is entirely the author’s opinion of their relative goodness/badness.

S	XChaCha20-Poly1305, AES-GCM-SIV
A	AES-GCM, ChaCha20-Poly1305
B	AES-SIV
C	AES-CTR + HMAC-SHA2, AES-CBC + HMAC-SHA2
D	AES-CCM
F	Any: AES-ECB, RC4, Blowfish Unauthenticated: AES-CBC, AES-CTR, Salsa20, ChaCha

Soatok’s ranking of symmetric encryption methods
https://soatok.blog/2020/07/12/comparison-of-symmetric-encryption-methods/

#AEAD #AES #AESGCM #AESGCMSIV #ChaCha20Poly1305 #ciphers #comparison #cryptography #encryption #NMRAEAD #ranking #SecurityGuidance #streamCiphers #symmetricCryptography #symmetricEncryption #XChaCha20Poly1305