Wikipedia’s definition of a digital signature is:

A digital signature is a mathematical scheme for verifying the authenticity of digital messages or documents. A valid digital signature on a message gives a recipient confidence that the message came from a sender known to the recipient.

—Wikipedia

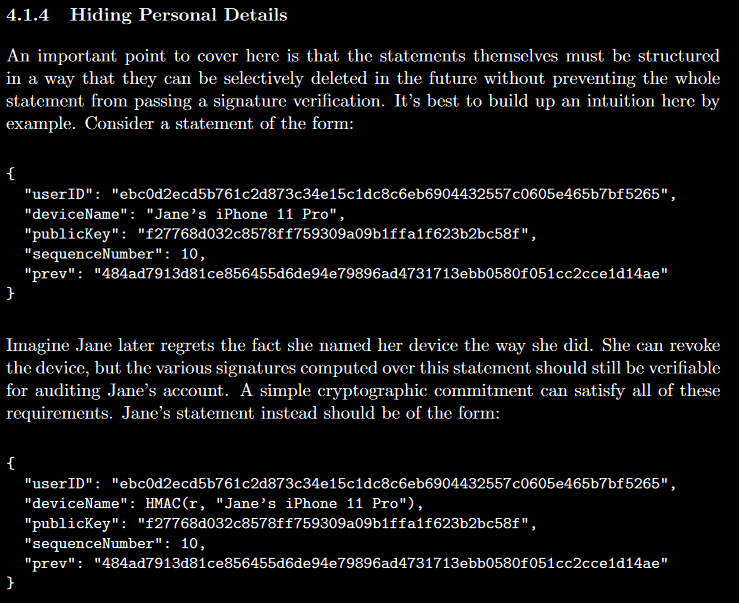
They also have a handy diagram of the process by which digital signatures are created and verified: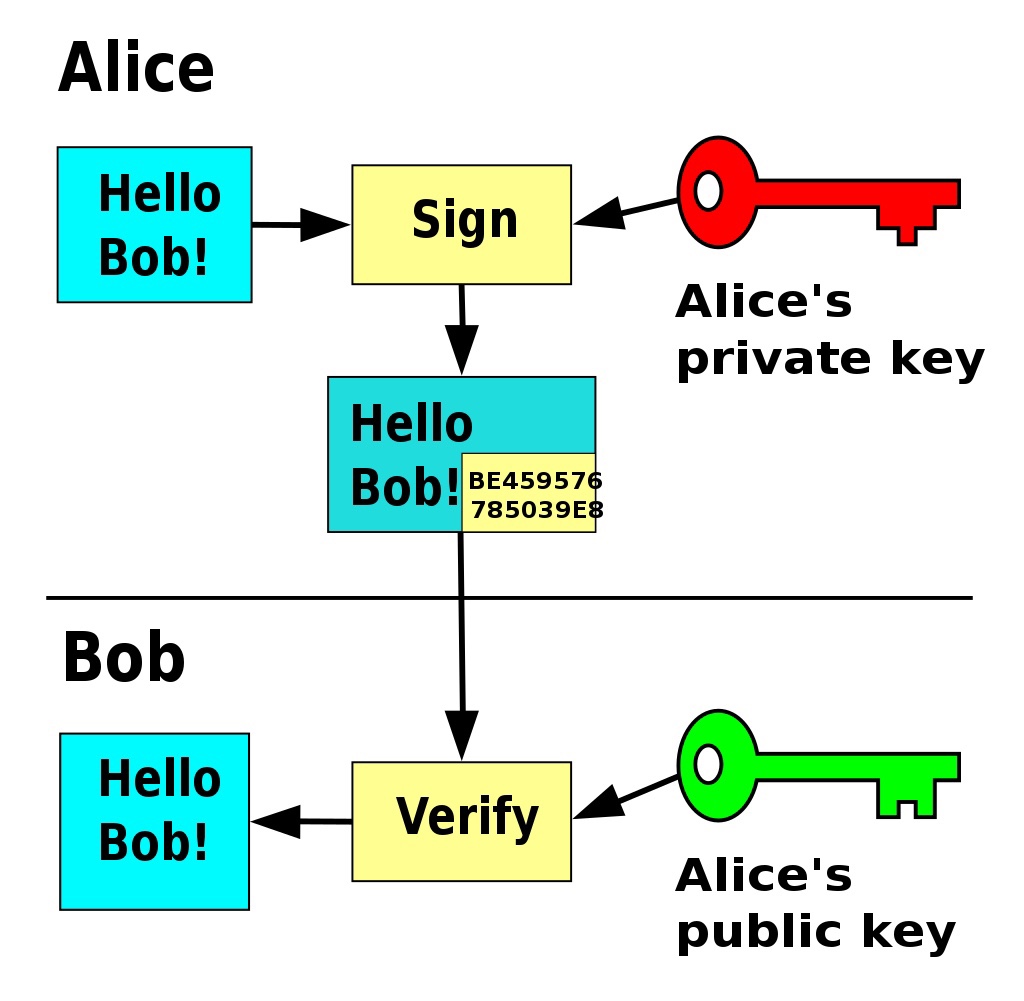
Source: https://commons.m.wikimedia.org/wiki/File😛rivate_key_signing.svg#mw-jump-to-license (CC-BY-SA)
Alice signs a message using her private key and Bob can then verify that the message came from Alice, and hasn’t been tampered with, using her public key. This all seems straightforward and uncomplicated and is probably most developers’ view of what signatures are for and how they should be used. This has led to the widespread use of signatures for all kinds of things: validating software updates, authenticating SSL connections, and so on.

But cryptographers have a different way of looking at digital signatures that has some surprising aspects. This more advanced way of thinking about digital signatures can tell us a lot about what are appropriate, and inappropriate, use-cases.

Identification protocols

There are several ways to build secure signature schemes. Although you might immediately think of RSA, the scheme perhaps most beloved by cryptographers is Schnorr signatures. These form the basis of modern EdDSA signatures, and also (in heavily altered form) DSA/ECDSA.

The story of Schnorr signatures starts not with a signature scheme, but instead with an interactive identification protocol. An identification protocol is a way to prove who you are (the “prover”) to some verification service (the “verifier”). Think logging into a website. But note that the protocol is only concerned with proving who you are, not in establishing a secure session or anything like that.

There are a whole load of different ways to do this, like sending a username and password or something like WebAuthn/passkeys (an ironic mention that we’ll come back to later). One particularly elegant protocol is known as Schnorr’s protocol. It’s elegant because it is simple and only relies on basic security conjectures that are widely accepted, and it also has some nice properties that we’ll mention shortly.

The basic structure of the protocol involves three phases: Commit-Challenge-Response. If you are familiar with challenge-response authentication protocols this just adds an additional commitment message at the start.

Alice (for it is she!) wants to prove to Bob who she is. Alice already has a long-term private key, a, and Bob already has the corresponding public key, A. These keys are in a Diffie-Hellman-like finite field or elliptic curve group, so we can say A = g^a mod p where g is a generator and p is the prime modulus of the group. The protocol then works like this:

1. Alice generates a random ephemeral key, r, and the corresponding public key R = g^r mod p. She sends R to Bob as the commitment.
2. Bob stores R and generates a random challenge, c and sends that to Alice.
3. Alice computes s = ac + r and sends that back to Bob as the response.
4. Finally, Bob checks if g^s = A^c * R (mod p). If it is then Alice has successfully authenticated, otherwise it’s an imposter. The reason this works is that g^s = g^(ac + r) and A^c * R = (g^a)^c * g^r = g^(ac + r) too. Why it’s secure is another topic for another day.

Don’t worry if you don’t understand all this. I’ll probably do a blog post about Schnorr identification at some point, but there are plenty of explainers online if you want to understand it. For now, just accept that this is indeed a secure identification scheme. It has some nice properties too.

One is that it is a (honest-verifier) zero knowledge proof of knowledge (of the private key). That means that an observer watching Alice authenticate, and the verifier themselves, learn nothing at all about Alice’s private key from watching those runs, but the verifier is nonetheless convinced that Alice knows it.

This is because it is easy to create valid runs of the protocol for any private key by simply working backwards rather than forwards, starting with a response and calculating the challenge and commitment that fit that response. Anyone can do this without needing to know anything about the private key. That is, for any given challenge you can find a commitment for which it is easy to compute the correct response. (What they cannot do is correctly answer a random challenge after they’ve already sent a commitment). So they learn no information from observing a genuine interaction.

Fiat-Shamir

So what does this identification protocol have to do with digital signatures? The answer is that there is a process known as the Fiat-Shamir heuristic by which you can automatically transform certain interactive identification protocols into a non-interactive signature scheme. You can’t do this for every protocol, only ones that have a certain structure, but Schnorr identification meets the criteria. The resulting signature scheme is known, amazingly, as the Schnorr signature scheme.

You may be relieved to hear that the Fiat-Shamir transformation is incredibly simple. We basically just replace the challenge part of the protocol with a cryptographic hash function, computed over the message we want to sign and the commitment public key: c = H(R, m).

That’s it. The signature is then just the pair (R, s).

Note that Bob is now not needed in the process at all and Alice can compute this all herself. To validate the signature, Bob (or anyone else) recomputes c by hashing the message and R and then performs the verification step just as in the identification protocol.

Schnorr signatures built this way are secure (so long as you add some critical security checks!) and efficient. The EdDSA signature scheme is essentially just a modern incarnation of Schnorr with a few tweaks.

What does this tell us about appropriate uses of signatures

The way I’ve just presented Schnorr signatures and Fiat-Shamir is the way they are usually presented in cryptography textbooks. We start with an identification protocol, performed a simple transformation and ended with a secure signature scheme. Happy days! These textbooks then usually move on to all the ways you can use signatures and never mention identification protocols again. But the transformation isn’t an entirely positive process: a lot was lost in translation!

There are many useful aspects of interactive identification protocols that are lost by signature schemes:

• A protocol run is only meaningful for the two parties involved in the interaction (Alice and Bob). By contrast a signature is equally valid for everyone.
• A protocol run is specific to a given point in time. Alice’s response is to a specific challenge issued by Bob just prior. A signature can be verified at any time.

These points may sound like bonuses for signature schemes, but they are actually drawbacks in many cases. Signatures are often used for authentication, where we actually want things to be tied to a specific interaction. This lack of context in signatures is why standards like JWT have to add lots of explicit statements such as audience and issuer checks to ensure the JWT came from the expected source and arrived at the intended destination, and expiry information or unique identifiers (that have to be remembered) to prevent replay attacks. A significant proportion of JWT vulnerabilities in the wild are caused by developers forgetting to perform these checks.

WebAuthn is another example of this phenomenon. On paper it is a textbook case of an identification protocol. But because it is built on top of digital signatures it requires adding a whole load of “contextual bindings” for similar reasons to JWTs. Ironically, the most widely used WebAuthn signature algorithm, ECDSA, is itself a Schnorr-ish scheme.

TLS also uses signatures for what is essentially an identification protocol, and similarly has had a range of bugs due to insufficient context binding information being included in the signed data. (SSL also uses signatures for verifying certificates, which is IMO a perfectly good use of the technology. Certificates are exactly a case of where you want to convert an interactive protocol into a non-interactive one. But then again we also do an interactive protocol (DNS) in that case anyway 🤷).

In short, an awful lot of uses of digital signatures are actually identification schemes of one form or another and would be better off using an actual identification scheme. But that doesn’t mean using something like Schnorr’s protocol! There are actually better alternatives that I’ll come back to at the end.

Special Soundness: fragility by design

Before I look at alternatives, I want to point out that pretty much all in-use signature schemes are extremely fragile in practice. The zero-knowledge security of Schnorr identification is based on it having a property called special soundness. Special soundness essentially says that if Alice accidentally reuses the same commitment (R) for two runs of the protocol, then any observer can recover her private key.

This sounds like an incredibly fragile notion to build into your security protocol! If I accidentally reuse this random value then I leak my entire private key??! And in fact it is: such nonce-reuse bugs are extremely common in deployed signature systems, and have led to compromise of lots of private keys (eg Playstation 3, various Bitcoin wallets etc).

But despite its fragility, this notion of special soundness is crucial to the security of many signature systems. They are truly a cursed technology!

To solve this problem, some implementations and newer standards like EdDSA use deterministic commitments, which are based on a hash of the private key and the message. This ensures that the commitment will only ever be the same if the message is identical: preventing the private key from being recovered. Unfortunately, such schemes turned out to be more susceptible to fault injection attacks (a much less scalable or general attack vector), and so now there are “hedged” schemes that inject a bit of randomness back into the hash. It’s cursed turtles all the way down.

If your answer to this is to go back to good old RSA signatures, don’t be fooled. There are plenty of ways to blow your foot off using old faithful, but that’s for another post.

Did you want non-repudiation with that?

Another way that signatures cause issues is that they are too powerful for the job they are used for. You just wanted to authenticate that an email came from a legitimate server, but now you are providing irrefutable proof of the provenance of leaked private communications. Oops!

Signatures are very much the hammer of cryptographic primitives. As well as authenticating a message, they also provide third-party verifiability and (part of) non-repudiation.

You don’t need to explicitly want anonymity or deniability to understand that these strong security properties can have damaging and unforeseen side-effects. Non-repudiation should never be the default in open systems.

I could go on. From the fact that there are basically zero acceptable post-quantum signature schemes (all way too large or too risky), to issues with non-canonical signatures and cofactors and on and on. The problems of signature schemes never seem to end.

What to use instead?

Ok, so if signatures are so bad, what can I use instead?

Firstly, if you can get away with using a simple shared secret scheme like HMAC, then do so. In contrast to public key crypto, HMAC is possibly the most robust crypto primitive ever invented. You’d have to go really far out of your way to screw up HMAC. (I mean, there are timing attacks and that time that Bouncy Castle confused bits and bytes and used 16-bit HMAC keys, so still do pay attention a little bit…)

If you need public key crypto, then… still use HMAC. Use an authenticated KEM with X25519 to generate a shared secret and use that with HMAC to authenticate your message. This is essentially public key authenticated encryption without the actual encryption. (Some people mistakenly refer to such schemes as designated verifier signatures, but they are not).

Signatures are good for software/firmware updates and pretty terrible for everything else.

https://neilmadden.blog/2024/09/18/digital-signatures-and-how-to-avoid-them/

#authenticatedEncryption #cryptography #misuseResistance #signatures

Neil Madden

2021-02-16 13:14:46

In my previous post, I described the KEM/DEM paradigm for hybrid encryption. The key encapsulation mechanism is given the recipient’s public key and outputs a fresh AES key and an encapsulation of that key that the recipient can decapsulate to recover the AES key. In this post I want to talk about several ways that the KEM interface falls short and what to do about it:

• As I’ve discussed before, the standard definition of public key encryption lacks any authentication of the sender, and the KEM-DEM paradigm is no exception. You often want to have some idea of where a message came from before you process it, so how can we add sender authentication?
• If you want to send the same message to multiple recipients, a natural approach would be to encrypt the message once with a fresh AES key and then encrypt the AES key for each recipient. With the KEM approach though we’ll end up with a separate AES key for each recipient. How can we send the same message to multiple recipients without encrypting the whole thing separately for each one?
• Finally, the definition of public key encryption used in the KEM/DEM paradigm doesn’t provide forward secrecy. If an attacker ever compromises the recipient’s long-term private key, they can decrypt every message ever sent to that recipient. Can we prevent this?

In this article I’ll tackle the first two issues and show how the KEM/DEM abstractions can be adjusted to cope with each. In a follow-up post I’ll then show how to tackle forward secrecy, along with replay attacks and other issues. Warning: this post is longer and has more technical details than the previous post. It’s really meant for people who already have some experience with cryptographic algorithms.

Authenticated KEMs

Let’s look first at how to create authenticated encryption in the KEM/DEM paradigm. The DEM used to encrypt the body of a message in the KEM/DEM paradigm already provides authenticated encryption, so the only work that needs to be done is to authenticate the KEM so that the recipient can be confident the encapsulated DEM key came from a trusted source. Although we could try to manually combine a KEM with some kind of authentication mechanism, it’s almost always better to define a single abstraction that provides both properties. In this case, we can extend our KEM interface to become an authenticated KEM or AKEM. An AKEM is like a KEM, but the encapsulation function takes the sender’s private key as an additional argument, and the decapsulation function takes the sender’s public key:
function auth_encapsulate(senderPrivateKey, recipientPublicKey): // returns (aesKey, encapsulatedKey) as beforefunction auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey): // returns either the original aesKey or an error if // authentication fails
A straightforward implementation of this idea would be to combine an existing (unauthenticated) KEM with a signature scheme. The KEM produces an encapsulated key, which we then sign with our private key so that the recipient can be sure that it really came from us:
function auth_encapsulate_sig(senderPrivateKey, recipientPublicKey): var (aesKey, encapsulatedKey) = KEM.encapsulate(recipientPublicKey); var signature = sign(senderPrivateKey, encapsulatedKey); return (aesKey, encapsulatedKey || signature);function auth_decapsulate_sig(senderPublicKey, recipientPrivateKey, encapsulatedSignedKey): var (encapsulatedKey, signature) = parse(encapsulatedSignedKey); if !verify_signature(senderPublicKey, encapsulatedKey, signature): return error; return KEM.decapsulate(recipientPrivateKey, encapsulatedKey);
This works, but it can produce very large encapsulated keys. For example, if you use RSA-KEM with an RSA signature scheme and 3072-bit keys, then the encapsulated key will end up being at least 768 bytes long. We can do better by removing the explicit signature and instead using implicit authentication, where we derive the DEM key in such a way that only the genuine sender could have calculated it. Any attempt to change the encapsulated key, without using the sender’s private key, will result in a different DEM key being calculated and the DEM authenticated decryption step will fail with an authentication error.

One way to achieve this is to adapt the elliptic curve Diffie-Hellman (ECDH) KEM to include the sender’s private key in the key agreement calculation. Rather than performing a single ECDH calculation between an ephemeral private key and the recipient’s public key, we additionally perform one between the sender’s private key and the recipient’s public key. The two derived shared secrets are then concatenated before being fed into the Key Derivation Function to produce the AES key:
function auth_encapsulate_ecdh(senderPrivateKey, recipientPublicKey): var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(recipientPublicKey.curve); var ess = ecdh(ephemeralSecretKey, recipientPublicKey); var sss = ecdh(senderPrivateKey, recipientPublicKey); var aesKey = sha256(ess || sss || ephemeralPublicKey); return (aesKey, ephemeralPublicKey);function ecdh_decapsulate_ecdh(senderPublicKey, recipientPrivateKey, ephemeralPublicKey): var ess = ecdh(recipientPrivateKey, ephemeralPublicKey); var sss = ecdh(recipientPrivateKey, senderPublicKey); return sha256(ess || sss || ephemeralPublicKey);
(Note: as before we include the ephemeral public key in the KDF step to ensure non-malleability, and we’re using SHA-256 as a cheap and cheerful stand-in for a real KDF).

The advantage of this approach is that the encapsulated key is still just an ephemeral public key—just 32 bytes for X25519. It’s also more deniable than the signature version. NIST call this scheme the One-Pass Unified Model, and it’s also broadly similar to the Noise “K” one-way handshake pattern and the AKEM defined for the upcoming HPKE standard. Although this scheme is more compact than the combination of a KEM plus a signature, it is still computationally quite expensive because of the two ECDH computations that are needed. More efficient options such as (one-pass) MQV can reduce this overhead, but these are not widely used in practice due to patent issues and potential weaknesses of some variants.

Both of these AKEM designs suffer from some security weaknesses:

• They are both vulnerable to something called Key Compromise Impersonation (KCI) attacks. What this means is that if an attacker compromises your long-term secret key, they can not only pretend to be you when sending messages to other people, but can pretend to be anyone else when sending messages to you! For the ECDH scheme they can immediately do this. The KEM-then-sign variant is a bit stronger, in that an attacker would have to capture at least one message sent to you by the party they want to impersonate, but in practice this is often possible. Preventing KCI generally involves either an interactive authentication protocol or signing the entire message, both of which I’ll leave out of this article.
• Neither design incorporates any notion of the identity of the users involved. In some cases this can lead to Unknown Key Share attacks, in which we think we’re communicating with Alice but actually are talking to Bob. You can solve this problem by including identity information and long-term public keys in the signature or key-derivation steps. It can be useful to add a general “context” argument to the encapsulate and decapsulate functions to allow additional data to be included in the KDF:

function auth_encapsulate_ecdh(senderPrivateKey, recipientPublicKey, context): var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(recipientPublicKey.curve); var ess = ecdh(ephemeralSecretKey, recipientPublicKey); var sss = ecdh(senderPrivateKey, recipientPublicKey); var aesKey = sha256(ess || sss || ephemeralPublicKey || context); return (aesKey, ephemeralPublicKey);function ecdh_decapsulate_ecdh(senderPublicKey, recipientPrivateKey, ephemeralPublicKey, context): var ess = ecdh(recipientPrivateKey, ephemeralPublicKey); var sss = ecdh(recipientPrivateKey, senderPublicKey); return sha256(ess || sss || ephemeralPublicKey || context);

Sending to multiple recipients

The basic KEM/DEM paradigm runs into a problem if we want to send the same message to multiple recipients. In the traditional approach to hybrid encryption before KEMs, you’d simply generate a random AES key and then encrypt it for each recipient. But this doesn’t work for KEMs: we’d have to run the KEM separately for each recipient, obtaining a separate AES key for each one, and then encrypt the entire message with each AES key. This is very inefficient.

We can solve this problem by introducing a notion called symmetric key-wrapping, where we use one AES key to encrypt (“wrap”) another AES key. In principle, any secure authenticated encryption scheme (such as a DEM) could be used, but there are some specialised algorithms that are more compact.

The idea is a bit like the original version of hybrid encryption, but instead of directly encrypting the AES key for each recipient, we will instead use the KEM to derive a key-encryption key (KEK) for each recipient, and then use that to encrypt the random AES key (which we’ll call the Data Encryption Key, or DEK):

1. Generate a random DEK, dek = DEM.keygen()
2. Encrypt the message with dk: ciphertext = DEM.encrypt(dek, message);
3. For each recipient, r, calculate the Key Encryption Key:
   kek[r], encapsulatedKey[r] = KEM.encapsulate(r.publicKey);
4. For each KEK, encrypt the DEK: wrappedKey[r] = wrap(kek[r], dk);
5. Send the encrypted ciphertext, the wrapped keys, and the encapsulated keys to the recipients.

Each recipient then runs the KEM to decapsulate their encapsulated key and uses the result to decrypt (“unwrap”) the DEK. They then use the DEK to decrypt the rest of the message.

There is still an inefficiency here though, in that we’ll have a separate encapsulated key for each recipient. For the ECDH-KEM the encapsulated key is an ephemeral public key, and we can safely reuse the same ephemeral key pair for every recipient. This saves a costly key-pair generation step for each recipient and reduces the size of the final ciphertext, but we can’t achieve this with the existing KEM API.

Once again, we can adapt the KEM interface to natively support this. The encapsulation function is changed to take a set of public keys for the recipients rather than just one. The result is known as an mKEM, and you can find more details in this article by Nigel Smart (*cough* over here). For example, here’s an unauthenticated mKEM based on ECDH:
function mkem_encapsulate(recipientPublicKeys): var aesKey = DEM.keygen(); var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(); var wrappedKeys = []; for pk in recipientPublicKeys: var ss = ecdh(ephemeralSecretKey, pk); var kek = sha256(ss || ephemeralPublicKey); var wrappedKey = wrap(kek, aesKey); wrappedKeys += wrappedKey; end return (aesKey, ephemeralPublicKey || wrappedKeys);

Authenticated mKEMs

It’s easy to see how we could adapt the generic mKEM approach of the previous section to provide authenticated encryption (AmKEM? mAKEM?): simply add the sender’s private key to the interface and then perform an authenticated key derivation for each recipient, just as we did for the single-recipient AKEM:
function auth_mkem_encapsulate(senderPrivateKey, recipientPublicKeys): var aesKey = DEM.keygen(); var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(); var wrappedKeys = []; for pk in recipientPublicKeys: var ess = ecdh(ephemeralSecretKey, pk); var sss = ecdh(senderPrivateKey, pk); var kek = sha256(ess || sss || ephemeralPublicKey); var wrappedKey = wrap(kek, aesKey); wrappedKeys += wrappedKey; end return (aesKey, ephemeralPublicKey || wrappedKeys);
This does provide authenticated encryption, but only if all the recipients are honest. If any of the recipients is malicious, or have had their private key compromised, they can create a new message that appears to come from the original sender:

• First they decapsulate the genuine message to obtain the DEM key, dek.
• They then create a new message and encrypt it using the DEM and the same DEK: var c2 = DEM.encrypt(dek, "My new message");
• Finally, they re-attach the wrapped keys and ephemeral public key from the original message and send the whole thing to the same recipients (or a subset of them).

When the recipients decrypt the message it will appear that it is a genuine message from the original sender. This can happen regardless of whether you use signatures or implicit authentication in the AKEM. The fundamental reason is that neither the encapsulated keys nor the wrapped keys are in any way tied to the actual message. The KEM ensures the authenticity of the data encryption key, and the DEM ensures that a message could only have been created by someone who had access to that DEK. The problem is that the set of people who have access to the DEK is the original sender and all of the recipients.

Protecting against this kind of attack is known as insider security, and to solve it we’ll need to give up some measure of deniability. We could just sign the entire message, in which case we give up all deniability: any third party can verify that we sent that message, not just our intended recipients. Let’s call this outsider non-repudiation. What we really want is a slightly weaker guarantee: the recipients can prove to each other that the message came from the original sender (or didn’t in the case of a forgery), but they can’t prove that to anyone outside the group. We’ll call this insider non-repudiation.

For example, if Alice sends a message to Bob and Charlie, then Bob can prove to Charlie that Alice really did send that message (even if Charlie failed to receive it), but Bob can’t prove anything about the origin of the message to Delilah, who wasn’t in the original set of recipients. As far as Delilah is concerned, Bob could have fabricated the message.

It turns out that we can quite easily solve this problem, but first we need a little detour.

Tag-KEM: KEMs with associated data

The original formulation of the KEM/DEM paradigm required both the KEM and the DEM to be secure against chosen ciphertext attacks (CCA). This is a strong notion of security, but was found to be too strong in some cases. There are efficient hybrid encryption schemes in which either the KEM or the DEM is not CCA-secure, but when combined in the right way can achieve CCA-secure public key encryption. Some of these schemes are more efficient than they would be otherwise. To accommodate these schemes into the KEM/DEM paradigm, a new variant known as Tag-KEM was introduced. A Tag-KEM (TKEM) splits the encapsulation of a symmetric key into two phases:

• First, a function is called with the recipient’s public key and it outputs an AES key to use with the DEM and a private state value:
  var (aesKey, state) = TKEM.key(recipientPublicKey);
• Then, after the message has been encrypted with the DEM, a second function of the TKEM is called to generate an encapsulated key from the internal state and a tag. The tag is some arbitrary associated data that will be linked to the encapsulated key. You can think of it a bit like the context argument we added earlier to allow user identities to be bound to the encapsulated key.
  var encapsulatedKey = TKEM.encapsulate(state, tag);
• To decapsulate the key, the recipient has to provide the same tag. If they provide a different tag then an error is returned.

In the original paper, this is used to allow the DEM to be a simple CPA-secure (unauthenticated) encryption algorithm. The entire encrypted ciphertext from the DEM is passed in as the tag to the TKEM. The TKEM then applies a MAC to the tag as part of the encapsulation process, effectively transforming it into a secure Encrypt-then-MAC scheme. We can use the same mechanism to ensure that the key encapsulation is tied to the message to prevent insider attacks against authenticated KEMs, by ensuring that the tag is included in the authentication step. The same idea has been used to construct secure signcryption schemes from Tag-KEM (signcryption is a strong form of public key authenticated encryption that provides the same authenticity guarantees as a signature, and so provides the stronger outsider non-repudiation we want to avoid).

There are two ways that we could accomplish this:

• We can add a tag argument to the AKEM mechanism, so that the tag is directly included in the authentication provided by the AKEM. For example, using the context argument we described earlier. If the AKEM is based on signatures, then this effectively becomes a signcryption scheme, which has the advantage of also preventing KCI attacks, but destroys deniability.
• If we are using key-wrapping, and the key-wrapping function allows associated data (SIV-AES does, AES-KW doesn’t) then we can include the tag there instead. This better preserves deniability, but remains vulnerable to KCI.

If we’re using a KEM based on ECDH with a strong KDF like HKDF, then these two options are pretty similar: the tag ends up getting included in a strong MAC (PRF) protected by a key known only to the sender and an individual recipient. If the tag is the whole message, then this ensures that a new message can’t be created with the same encapsulated DEK without the other recipients being able to detect this.

mATKEMs

Putting it all together, we’d get a multi-recipient authenticated Tag-KEM, or mATKEM for short! A mATKEM has the following functions:

• keygen() – generates public and private keys for a sender/recipient and returns them.
• key(senderPrivateKey, recipientPublicKeys) – returns a fresh DEM key and a private state object that is tied to the sender, recipients, and the DEM key.
• auth_encapsulate(state, tag) – encapsulates the DEM key for each of the recipients in a way that they can authenticate the sender, with the tag also authenticated (but not encapsulated). Returns the encapsulated key.
• auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey, tag) – authenticates that the encapsulated key was produced by the given sender with the given tag, and then decapsulates and returns the DEM key. If authentication fails then an error is returned instead.

A sketch of an implementation of a secure mATKEM based on ECDH with key-wrapping is shown below. This is just a sketch of how such a thing could be implemented, I haven’t rigorously analysed it or attempted to prove it correct.
function key(senderPrivateKey, recipientPublicKeys): var dek = DEM.keygen(); var state = (dek, senderPrivateKey, recipientPublicKeys); return (dek, state);function auth_encapsulate(state, tag): var (dek, senderPrivateKey, recipientPublicKeys) = state; var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(); var wrappedKeys = []; for pk in recipientPublicKeys: var ess = ecdh(ephemeralSecretKey, pk); var sss = ecdh(senderPrivateKey, pk); var kek = KDF(ess || sss || ephemeralPublicKey || tag); var wrappedKey = wrap(kek, dek); wrappedKeys += wrappedKey; end return ephemeralPublicKey || wrappedKeys;function auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey, tag): var ephemeralPublicKey || wrappedKeys = encapsulatedKey; var ess = ecdh(recipientPrivateKey, ephemeralPublicKey); var sss = ecdh(recipientPrivateKey, senderPublicKey); var kek = KDF(ess || sss || ephemeralPublicKey || tag); for wrappedKey in wrappedKeys: var dek = unwrap(kek, wrappedKey); if dek != error: return dek end return error;

Compactly committing DEMs

In the original formulation of a Tag-KEM, the tag input is the full ciphertext output of the (unauthenticated) DEM. But in the mATKEM implementation this entire ciphertext gets passed into the KDF or MAC for every recipient, which is very inefficient for long messages. This can be optimised in the multi-recipient case by hashing the tag once with a collision-resistant hash function rather than including the whole ciphertext in the KEM or key-wrap calculation for every recipient.

An alternative approach would be to use an authenticated DEM that is compactly committing (which I’ll refer to as ccDEM) and then use the MAC tag from the DEM as the tag for the authenticated TKEM. The advantage of reusing the authentication tag from the DEM rather than calculating it in the KEM, is that it allows us to use DEM schemes that are not based on Encrypt-then-MAC, for example misuse-resistant modes like SIV-AES.

Not all authenticated encryption algorithms are compactly committing, and several popular algorithms such as AES-GCM and ChaCha20-Poly1305 are definitely not. Although those algorithms prevent an attacker who doesn’t know the DEK from altering or forging new ciphertexts, if the attacker does know the key (as in insider security) then they can actually find other messages that have the same tag. The same is true for CMAC used by SIV and CCM. The definition of a compactly committing encryption algorithm requires that the MAC is a collision-resistant pseudorandom function (PRF) such as HMAC. If we assume that Alice (the sender) is honest then we should be able to get away with just second-preimage resistance instead for this application, which allows us to use shorter tags.

A ccDEM would be a DEM that takes a key, message, and (optional) associated data and returns a ciphertext and compactly committing authentication tag. An insider-secure multi-recipient authenticated public key encryption scheme (phew!) can then be built as the following generic composition:
function encrypt(senderPrivateKey, recipientPublicKeys, plaintext): var (dek, state) = mATKEM.key(senderPrivateKey, recipientPublicKeys); var (ciphertext, tag) = ccDEM.encrypt(dek, plaintext); var encapsulatedKey = mATKEM.auth_encapsulate(state, tag); return (encapsulatedKey, ciphertext, tag);function decrypt(senderPublicKey, recipientPrivateKey, receivedMessage): var (encapsulatedKey, ciphertext, tag) = receivedMessage; var dek = mATKEM.auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey, tag); if dek = error: return error; return DEM.decrypt(dek, ciphertext, tag);
The combination of a compactly committing DEM and an authenticated Tag-KEM seems like a powerful way of thinking about secure public key encryption schemes. This was first suggested to me by Paul Grubbs on the CFRG mailing list, but as he says it has not been formally analysed so please don’t rush to deploy such a scheme in production. Hopefully a real cryptographer will find this problem interesting and decide to fill in the gaps.

That concludes this look at building authenticated KEMs for multiple recipients. We’ve seen how the original KEM interface can be adapted to accommodate stronger security goals. As with the original KEM proposal, finding the right API is an important part of building secure software, and the wrong API can leave you constantly fighting subtle security issues or inefficiencies. In the next article, I look at forward secrecy and how that tantalising state argument in the Tag-KEM API can be a bridge towards secure interactive protocols like Signal or Noise.

https://neilmadden.blog/2021/02/16/when-a-kem-is-not-enough/

#authenticatedEncryption #cryptography #kemDemParadigm #publicKeyEncryption

In my previous post, I described the KEM/DEM paradigm for hybrid encryption. The key encapsulation mechanism is given the recipient’s public key and outputs a fresh AES key and an encapsulation of that key that the recipient can decapsulate to recover the AES key. In this post I want to talk about several ways that the KEM interface falls short and what to do about it:

• As I’ve discussed before, the standard definition of public key encryption lacks any authentication of the sender, and the KEM-DEM paradigm is no exception. You often want to have some idea of where a message came from before you process it, so how can we add sender authentication?
• If you want to send the same message to multiple recipients, a natural approach would be to encrypt the message once with a fresh AES key and then encrypt the AES key for each recipient. With the KEM approach though we’ll end up with a separate AES key for each recipient. How can we send the same message to multiple recipients without encrypting the whole thing separately for each one?
• Finally, the definition of public key encryption used in the KEM/DEM paradigm doesn’t provide forward secrecy. If an attacker ever compromises the recipient’s long-term private key, they can decrypt every message ever sent to that recipient. Can we prevent this?

In this article I’ll tackle the first two issues and show how the KEM/DEM abstractions can be adjusted to cope with each. In a follow-up post I’ll then show how to tackle forward secrecy, along with replay attacks and other issues. Warning: this post is longer and has more technical details than the previous post. It’s really meant for people who already have some experience with cryptographic algorithms.

Authenticated KEMs

Let’s look first at how to create authenticated encryption in the KEM/DEM paradigm. The DEM used to encrypt the body of a message in the KEM/DEM paradigm already provides authenticated encryption, so the only work that needs to be done is to authenticate the KEM so that the recipient can be confident the encapsulated DEM key came from a trusted source. Although we could try to manually combine a KEM with some kind of authentication mechanism, it’s almost always better to define a single abstraction that provides both properties. In this case, we can extend our KEM interface to become an authenticated KEM or AKEM. An AKEM is like a KEM, but the encapsulation function takes the sender’s private key as an additional argument, and the decapsulation function takes the sender’s public key:
function auth_encapsulate(senderPrivateKey, recipientPublicKey): // returns (aesKey, encapsulatedKey) as beforefunction auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey): // returns either the original aesKey or an error if // authentication fails
A straightforward implementation of this idea would be to combine an existing (unauthenticated) KEM with a signature scheme. The KEM produces an encapsulated key, which we then sign with our private key so that the recipient can be sure that it really came from us:
function auth_encapsulate_sig(senderPrivateKey, recipientPublicKey): var (aesKey, encapsulatedKey) = KEM.encapsulate(recipientPublicKey); var signature = sign(senderPrivateKey, encapsulatedKey); return (aesKey, encapsulatedKey || signature);function auth_decapsulate_sig(senderPublicKey, recipientPrivateKey, encapsulatedSignedKey): var (encapsulatedKey, signature) = parse(encapsulatedSignedKey); if !verify_signature(senderPublicKey, encapsulatedKey, signature): return error; return KEM.decapsulate(recipientPrivateKey, encapsulatedKey);
This works, but it can produce very large encapsulated keys. For example, if you use RSA-KEM with an RSA signature scheme and 3072-bit keys, then the encapsulated key will end up being at least 768 bytes long. We can do better by removing the explicit signature and instead using implicit authentication, where we derive the DEM key in such a way that only the genuine sender could have calculated it. Any attempt to change the encapsulated key, without using the sender’s private key, will result in a different DEM key being calculated and the DEM authenticated decryption step will fail with an authentication error.

One way to achieve this is to adapt the elliptic curve Diffie-Hellman (ECDH) KEM to include the sender’s private key in the key agreement calculation. Rather than performing a single ECDH calculation between an ephemeral private key and the recipient’s public key, we additionally perform one between the sender’s private key and the recipient’s public key. The two derived shared secrets are then concatenated before being fed into the Key Derivation Function to produce the AES key:
function auth_encapsulate_ecdh(senderPrivateKey, recipientPublicKey): var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(recipientPublicKey.curve); var ess = ecdh(ephemeralSecretKey, recipientPublicKey); var sss = ecdh(senderPrivateKey, recipientPublicKey); var aesKey = sha256(ess || sss || ephemeralPublicKey); return (aesKey, ephemeralPublicKey);function ecdh_decapsulate_ecdh(senderPublicKey, recipientPrivateKey, ephemeralPublicKey): var ess = ecdh(recipientPrivateKey, ephemeralPublicKey); var sss = ecdh(recipientPrivateKey, senderPublicKey); return sha256(ess || sss || ephemeralPublicKey);
(Note: as before we include the ephemeral public key in the KDF step to ensure non-malleability, and we’re using SHA-256 as a cheap and cheerful stand-in for a real KDF).

The advantage of this approach is that the encapsulated key is still just an ephemeral public key—just 32 bytes for X25519. It’s also more deniable than the signature version. NIST call this scheme the One-Pass Unified Model, and it’s also broadly similar to the Noise “K” one-way handshake pattern and the AKEM defined for the upcoming HPKE standard. Although this scheme is more compact than the combination of a KEM plus a signature, it is still computationally quite expensive because of the two ECDH computations that are needed. More efficient options such as (one-pass) MQV can reduce this overhead, but these are not widely used in practice due to patent issues and potential weaknesses of some variants.

Both of these AKEM designs suffer from some security weaknesses:

• They are both vulnerable to something called Key Compromise Impersonation (KCI) attacks. What this means is that if an attacker compromises your long-term secret key, they can not only pretend to be you when sending messages to other people, but can pretend to be anyone else when sending messages to you! For the ECDH scheme they can immediately do this. The KEM-then-sign variant is a bit stronger, in that an attacker would have to capture at least one message sent to you by the party they want to impersonate, but in practice this is often possible. Preventing KCI generally involves either an interactive authentication protocol or signing the entire message, both of which I’ll leave out of this article.
• Neither design incorporates any notion of the identity of the users involved. In some cases this can lead to Unknown Key Share attacks, in which we think we’re communicating with Alice but actually are talking to Bob. You can solve this problem by including identity information and long-term public keys in the signature or key-derivation steps. It can be useful to add a general “context” argument to the encapsulate and decapsulate functions to allow additional data to be included in the KDF:

function auth_encapsulate_ecdh(senderPrivateKey, recipientPublicKey, context): var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(recipientPublicKey.curve); var ess = ecdh(ephemeralSecretKey, recipientPublicKey); var sss = ecdh(senderPrivateKey, recipientPublicKey); var aesKey = sha256(ess || sss || ephemeralPublicKey || context); return (aesKey, ephemeralPublicKey);function ecdh_decapsulate_ecdh(senderPublicKey, recipientPrivateKey, ephemeralPublicKey, context): var ess = ecdh(recipientPrivateKey, ephemeralPublicKey); var sss = ecdh(recipientPrivateKey, senderPublicKey); return sha256(ess || sss || ephemeralPublicKey || context);

Sending to multiple recipients

The basic KEM/DEM paradigm runs into a problem if we want to send the same message to multiple recipients. In the traditional approach to hybrid encryption before KEMs, you’d simply generate a random AES key and then encrypt it for each recipient. But this doesn’t work for KEMs: we’d have to run the KEM separately for each recipient, obtaining a separate AES key for each one, and then encrypt the entire message with each AES key. This is very inefficient.

We can solve this problem by introducing a notion called symmetric key-wrapping, where we use one AES key to encrypt (“wrap”) another AES key. In principle, any secure authenticated encryption scheme (such as a DEM) could be used, but there are some specialised algorithms that are more compact.

The idea is a bit like the original version of hybrid encryption, but instead of directly encrypting the AES key for each recipient, we will instead use the KEM to derive a key-encryption key (KEK) for each recipient, and then use that to encrypt the random AES key (which we’ll call the Data Encryption Key, or DEK):

1. Generate a random DEK, dek = DEM.keygen()
2. Encrypt the message with dk: ciphertext = DEM.encrypt(dek, message);
3. For each recipient, r, calculate the Key Encryption Key:
   kek[r], encapsulatedKey[r] = KEM.encapsulate(r.publicKey);
4. For each KEK, encrypt the DEK: wrappedKey[r] = wrap(kek[r], dk);
5. Send the encrypted ciphertext, the wrapped keys, and the encapsulated keys to the recipients.

Each recipient then runs the KEM to decapsulate their encapsulated key and uses the result to decrypt (“unwrap”) the DEK. They then use the DEK to decrypt the rest of the message.

There is still an inefficiency here though, in that we’ll have a separate encapsulated key for each recipient. For the ECDH-KEM the encapsulated key is an ephemeral public key, and we can safely reuse the same ephemeral key pair for every recipient. This saves a costly key-pair generation step for each recipient and reduces the size of the final ciphertext, but we can’t achieve this with the existing KEM API.

Once again, we can adapt the KEM interface to natively support this. The encapsulation function is changed to take a set of public keys for the recipients rather than just one. The result is known as an mKEM, and you can find more details in this article by Nigel Smart (*cough* over here). For example, here’s an unauthenticated mKEM based on ECDH:
function mkem_encapsulate(recipientPublicKeys): var aesKey = DEM.keygen(); var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(); var wrappedKeys = []; for pk in recipientPublicKeys: var ss = ecdh(ephemeralSecretKey, pk); var kek = sha256(ss || ephemeralPublicKey); var wrappedKey = wrap(kek, aesKey); wrappedKeys += wrappedKey; end return (aesKey, ephemeralPublicKey || wrappedKeys);

Authenticated mKEMs

It’s easy to see how we could adapt the generic mKEM approach of the previous section to provide authenticated encryption (AmKEM? mAKEM?): simply add the sender’s private key to the interface and then perform an authenticated key derivation for each recipient, just as we did for the single-recipient AKEM:
function auth_mkem_encapsulate(senderPrivateKey, recipientPublicKeys): var aesKey = DEM.keygen(); var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(); var wrappedKeys = []; for pk in recipientPublicKeys: var ess = ecdh(ephemeralSecretKey, pk); var sss = ecdh(senderPrivateKey, pk); var kek = sha256(ess || sss || ephemeralPublicKey); var wrappedKey = wrap(kek, aesKey); wrappedKeys += wrappedKey; end return (aesKey, ephemeralPublicKey || wrappedKeys);
This does provide authenticated encryption, but only if all the recipients are honest. If any of the recipients is malicious, or have had their private key compromised, they can create a new message that appears to come from the original sender:

• First they decapsulate the genuine message to obtain the DEM key, dek.
• They then create a new message and encrypt it using the DEM and the same DEK: var c2 = DEM.encrypt(dek, "My new message");
• Finally, they re-attach the wrapped keys and ephemeral public key from the original message and send the whole thing to the same recipients (or a subset of them).

When the recipients decrypt the message it will appear that it is a genuine message from the original sender. This can happen regardless of whether you use signatures or implicit authentication in the AKEM. The fundamental reason is that neither the encapsulated keys nor the wrapped keys are in any way tied to the actual message. The KEM ensures the authenticity of the data encryption key, and the DEM ensures that a message could only have been created by someone who had access to that DEK. The problem is that the set of people who have access to the DEK is the original sender and all of the recipients.

Protecting against this kind of attack is known as insider security, and to solve it we’ll need to give up some measure of deniability. We could just sign the entire message, in which case we give up all deniability: any third party can verify that we sent that message, not just our intended recipients. Let’s call this outsider non-repudiation. What we really want is a slightly weaker guarantee: the recipients can prove to each other that the message came from the original sender (or didn’t in the case of a forgery), but they can’t prove that to anyone outside the group. We’ll call this insider non-repudiation.

For example, if Alice sends a message to Bob and Charlie, then Bob can prove to Charlie that Alice really did send that message (even if Charlie failed to receive it), but Bob can’t prove anything about the origin of the message to Delilah, who wasn’t in the original set of recipients. As far as Delilah is concerned, Bob could have fabricated the message.

It turns out that we can quite easily solve this problem, but first we need a little detour.

Tag-KEM: KEMs with associated data

The original formulation of the KEM/DEM paradigm required both the KEM and the DEM to be secure against chosen ciphertext attacks (CCA). This is a strong notion of security, but was found to be too strong in some cases. There are efficient hybrid encryption schemes in which either the KEM or the DEM is not CCA-secure, but when combined in the right way can achieve CCA-secure public key encryption. Some of these schemes are more efficient than they would be otherwise. To accommodate these schemes into the KEM/DEM paradigm, a new variant known as Tag-KEM was introduced. A Tag-KEM (TKEM) splits the encapsulation of a symmetric key into two phases:

• First, a function is called with the recipient’s public key and it outputs an AES key to use with the DEM and a private state value:
  var (aesKey, state) = TKEM.key(recipientPublicKey);
• Then, after the message has been encrypted with the DEM, a second function of the TKEM is called to generate an encapsulated key from the internal state and a tag. The tag is some arbitrary associated data that will be linked to the encapsulated key. You can think of it a bit like the context argument we added earlier to allow user identities to be bound to the encapsulated key.
  var encapsulatedKey = TKEM.encapsulate(state, tag);
• To decapsulate the key, the recipient has to provide the same tag. If they provide a different tag then an error is returned.

In the original paper, this is used to allow the DEM to be a simple CPA-secure (unauthenticated) encryption algorithm. The entire encrypted ciphertext from the DEM is passed in as the tag to the TKEM. The TKEM then applies a MAC to the tag as part of the encapsulation process, effectively transforming it into a secure Encrypt-then-MAC scheme. We can use the same mechanism to ensure that the key encapsulation is tied to the message to prevent insider attacks against authenticated KEMs, by ensuring that the tag is included in the authentication step. The same idea has been used to construct secure signcryption schemes from Tag-KEM (signcryption is a strong form of public key authenticated encryption that provides the same authenticity guarantees as a signature, and so provides the stronger outsider non-repudiation we want to avoid).

There are two ways that we could accomplish this:

• We can add a tag argument to the AKEM mechanism, so that the tag is directly included in the authentication provided by the AKEM. For example, using the context argument we described earlier. If the AKEM is based on signatures, then this effectively becomes a signcryption scheme, which has the advantage of also preventing KCI attacks, but destroys deniability.
• If we are using key-wrapping, and the key-wrapping function allows associated data (SIV-AES does, AES-KW doesn’t) then we can include the tag there instead. This better preserves deniability, but remains vulnerable to KCI.

If we’re using a KEM based on ECDH with a strong KDF like HKDF, then these two options are pretty similar: the tag ends up getting included in a strong MAC (PRF) protected by a key known only to the sender and an individual recipient. If the tag is the whole message, then this ensures that a new message can’t be created with the same encapsulated DEK without the other recipients being able to detect this.

mATKEMs

Putting it all together, we’d get a multi-recipient authenticated Tag-KEM, or mATKEM for short! A mATKEM has the following functions:

• keygen() – generates public and private keys for a sender/recipient and returns them.
• key(senderPrivateKey, recipientPublicKeys) – returns a fresh DEM key and a private state object that is tied to the sender, recipients, and the DEM key.
• auth_encapsulate(state, tag) – encapsulates the DEM key for each of the recipients in a way that they can authenticate the sender, with the tag also authenticated (but not encapsulated). Returns the encapsulated key.
• auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey, tag) – authenticates that the encapsulated key was produced by the given sender with the given tag, and then decapsulates and returns the DEM key. If authentication fails then an error is returned instead.

A sketch of an implementation of a secure mATKEM based on ECDH with key-wrapping is shown below. This is just a sketch of how such a thing could be implemented, I haven’t rigorously analysed it or attempted to prove it correct.
function key(senderPrivateKey, recipientPublicKeys): var dek = DEM.keygen(); var state = (dek, senderPrivateKey, recipientPublicKeys); return (dek, state);function auth_encapsulate(state, tag): var (dek, senderPrivateKey, recipientPublicKeys) = state; var (ephemeralSecretKey, ephemeralPublicKey) = generateKeyPair(); var wrappedKeys = []; for pk in recipientPublicKeys: var ess = ecdh(ephemeralSecretKey, pk); var sss = ecdh(senderPrivateKey, pk); var kek = KDF(ess || sss || ephemeralPublicKey || tag); var wrappedKey = wrap(kek, dek); wrappedKeys += wrappedKey; end return ephemeralPublicKey || wrappedKeys;function auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey, tag): var ephemeralPublicKey || wrappedKeys = encapsulatedKey; var ess = ecdh(recipientPrivateKey, ephemeralPublicKey); var sss = ecdh(recipientPrivateKey, senderPublicKey); var kek = KDF(ess || sss || ephemeralPublicKey || tag); for wrappedKey in wrappedKeys: var dek = unwrap(kek, wrappedKey); if dek != error: return dek end return error;

Compactly committing DEMs

In the original formulation of a Tag-KEM, the tag input is the full ciphertext output of the (unauthenticated) DEM. But in the mATKEM implementation this entire ciphertext gets passed into the KDF or MAC for every recipient, which is very inefficient for long messages. This can be optimised in the multi-recipient case by hashing the tag once with a collision-resistant hash function rather than including the whole ciphertext in the KEM or key-wrap calculation for every recipient.

An alternative approach would be to use an authenticated DEM that is compactly committing (which I’ll refer to as ccDEM) and then use the MAC tag from the DEM as the tag for the authenticated TKEM. The advantage of reusing the authentication tag from the DEM rather than calculating it in the KEM, is that it allows us to use DEM schemes that are not based on Encrypt-then-MAC, for example misuse-resistant modes like SIV-AES.

Not all authenticated encryption algorithms are compactly committing, and several popular algorithms such as AES-GCM and ChaCha20-Poly1305 are definitely not. Although those algorithms prevent an attacker who doesn’t know the DEK from altering or forging new ciphertexts, if the attacker does know the key (as in insider security) then they can actually find other messages that have the same tag. The same is true for CMAC used by SIV and CCM. The definition of a compactly committing encryption algorithm requires that the MAC is a collision-resistant pseudorandom function (PRF) such as HMAC. If we assume that Alice (the sender) is honest then we should be able to get away with just second-preimage resistance instead for this application, which allows us to use shorter tags.

A ccDEM would be a DEM that takes a key, message, and (optional) associated data and returns a ciphertext and compactly committing authentication tag. An insider-secure multi-recipient authenticated public key encryption scheme (phew!) can then be built as the following generic composition:
function encrypt(senderPrivateKey, recipientPublicKeys, plaintext): var (dek, state) = mATKEM.key(senderPrivateKey, recipientPublicKeys); var (ciphertext, tag) = ccDEM.encrypt(dek, plaintext); var encapsulatedKey = mATKEM.auth_encapsulate(state, tag); return (encapsulatedKey, ciphertext, tag);function decrypt(senderPublicKey, recipientPrivateKey, receivedMessage): var (encapsulatedKey, ciphertext, tag) = receivedMessage; var dek = mATKEM.auth_decapsulate(senderPublicKey, recipientPrivateKey, encapsulatedKey, tag); if dek = error: return error; return DEM.decrypt(dek, ciphertext, tag);
The combination of a compactly committing DEM and an authenticated Tag-KEM seems like a powerful way of thinking about secure public key encryption schemes. This was first suggested to me by Paul Grubbs on the CFRG mailing list, but as he says it has not been formally analysed so please don’t rush to deploy such a scheme in production. Hopefully a real cryptographer will find this problem interesting and decide to fill in the gaps.

That concludes this look at building authenticated KEMs for multiple recipients. We’ve seen how the original KEM interface can be adapted to accommodate stronger security goals. As with the original KEM proposal, finding the right API is an important part of building secure software, and the wrong API can leave you constantly fighting subtle security issues or inefficiencies. In the next article, I look at forward secrecy and how that tantalising state argument in the Tag-KEM API can be a bridge towards secure interactive protocols like Signal or Noise.

https://neilmadden.blog/2021/02/16/when-a-kem-is-not-enough/

#authenticatedEncryption #cryptography #kemDemParadigm #publicKeyEncryption

Neil Madden

2021-01-22 14:29:47

If you know a bit about public key cryptography, you probably know that you don’t directly encrypt a message with a public key encryption algorithm like RSA. This is for many reasons, one of which being that it is incredibly slow. Instead you do what’s called hybrid encryption: first you generate a random AES key (*) and encrypt the message with that (using a suitable authenticated encryption mode), then you encrypt the AES key with the RSA public key. The recipient uses their RSA private key to decrypt the AES key and then uses that to decrypt the rest of the message. This is much faster than trying to encrypt a large message directly with RSA, so pretty much all sane implementations of RSA encryption do this.

But there’s a problem with this approach. An AES key is at most only 32 bytes long, while RSA wants to encrypt things that are approximately the same size as the modulus – i.e., 256 bytes for 2048-bit RSA keys, 384 bytes for 3072-bit keys, and so on. To make this work, we have to add some padding to the AES key until it is the right size. This sounds simple enough, but you may be surprised to find out that padding is one of the most dangerous things you can do in cryptography:

• Bleichenbacher’s attack against PKCS#1 v1.5 padding for RSA encryption broke SSL and SSH. It still regularly resurfaces.
• Padding oracle attacks against AES in CBC mode with PKCS#7 / PKCS#5 padding also broke SSL.
• Even after fixes were introduced, these attacks can often be revived using side-channel attacks or implementation flaws. Even improved padding schemes like OAEP, which were supposed to remove these attacks, have been found to be vulnerable in practice.

Although it’s possible to get padding right, the historical record is not good. So it would be really nice to not have to do this fiddly padding at all. But how can we do hybrid encryption without padding?

Key encapsulation

It turns out that we can do hybrid encryption without resorting to padding, by changing the way that we think about hybrid encryption. Rather than generating a fresh random AES key and then encrypting that with RSA, we can instead define an API that we call with the recipient’s public key and it returns a fresh AES key and it’s encrypted form all in one go. That is, rather than doing these two steps:
var aesKey = generate_aes_key();var encryptedKey = rsa_encrypt(aesKey, rsaPublicKey);
We instead do this one step:
var (aesKey, encryptedKey) = rsa_encapsulate(rsaPublicKey);
This new function is known as a Key Encapsulation Mechanism (KEM), and the change of API makes all the difference. The trick is that a KEM doesn’t have to directly encrypt the AES key. Instead it can encrypt something else from which the AES key can be derived. In particular, it can encrypt something that is exactly the right size for the RSA key being used, so no padding is required. This is exactly what RSA-KEM does. In RSA-KEM, the encapsulation mechanism generates a random value between 2 and n-1 (where n is the RSA modulus: a large number around 2048 bits or more), and then encrypts that using the RSA public key. The random number is then fed through a Key Derivation Function (KDF), which can be as simple as a secure hash function like SHA-256 (although there are better alternatives), to derive the AES key:
function rsa_encapsulate(publicKey): var random = generate_secure_random(2..publicKey.modulus-1); var encryptedKey = rsa_encrypt(random, publicKey); var aesKey = sha256(random); return (aesKey, encryptedKey);
Here rsa_encrypt is plain “textbook” RSA encryption with no padding. This would normally be completely insecure, but because the random value is the same size as the modulus it is secure in this case. Indeed, RSA-KEM has a nice proof of security (it’s pretty clear to see how an attack on RSA-KEM would imply an attack on RSA itself). The term “encapsulation” refers to the fact that an attacker doesn’t get to choose or even see the input to the RSA encryption function (the random value), only the output of the (one-way) hash function, which makes it much harder to attack.

The AES key is then used to encrypt the message and the encrypted message and the encapsulated key are both sent to the recipient. The recipient then decrypts the random value and runs it through the KDF again to recover the AES key:
function rsa_decapsulate(encryptedKey, rsaPrivateKey): var random = rsa_decrypt(encryptedKey, rsaPrivateKey); return sha256(random);

Data encapsulation

When a KEM is being used for hybrid encryption, it’s common to refer to encrypting the message with the derived AES key as the Data Encapsulation Mechanism (DEM). Because the KEM guarantees that a fresh key is returned every time, we can actually relax the security requirements of the symmetric encryption scheme to only provide one-time security. This means that you could, in theory, get away with using a constant nonce/IV for the encryption scheme, although I wouldn’t recommend this unless you know what you’re doing. (It’s too easy for a well-meaning developer to “optimise” the KEM to reuse the same value for a few messages).

Update (23 Jan): I found a nice paper from 2012 by G.M. Zaverucha that shows that the deterministic nature of a DEM leads to attacks in a multi-user setting, so a randomized symmetric encryption scheme should always be preferred.

The definition of a DEM ensures both confidentiality and integrity, and allows associated data to be authenticated but not encrypted. You can therefore think of it as (possibly deterministic) Authenticated Encryption with Associated Data (AEAD), which is the standard modern definition of symmetric encryption.

The KEM/DEM paradigm is then just the use of a KEM with a DEM to implement public key encryption:
function encrypt(message, publicKey): var (aesKey, encryptedKey) = kem.encapsulate(publicKey); var ciphertext = dem.encrypt(aesKey, message); return encryptedKey || ciphertext;
This combination is guaranteed to be secure against adaptive chosen ciphertext attacks if the KEM and DEM both are.

KEMs without RSA

Another advantage of the KEM approach is that it is much more natural to define KEMs for algorithms other than RSA. For example, you can easily define a KEM based on elliptic-curve Diffie-Hellman key agreement (ECDH):
function ecdh_encapsulate(recipientPublicKey): var (ephemeralSecret, ephemeralPublic) = generateKeyPair(recipientPublicKey.curve); var sharedSecret = ecdh(ephemeralSecret, recipientPublicKey); var aesKey = sha256(sharedSecret || ephemeralPublic); // NB "||" is concatenation return (aesKey, ephemeralPublic);function ecdh_decapsulate(ephemeralPublic, recipientPrivateKey): var sharedSecret = ecdh(recipientPrivateKey, ephemeralPublic); return sha256(sharedSecret || ephemeralPublic);
This corresponds to the widely-used ECIES encryption scheme (known as ECDH-ES in JOSE, for example). Here the “encryption” of the AES key is just an ephemeral public key, from which the AES key can be derived.

Summary

This approach and terminology, known as the KEM-DEM paradigm, was first proposed by Victor Shoup and has since become popular in academic cryptography. The basic idea, as shown in this article, is to combine generating a fresh random AES key and encrypting it into a single step. This turns out to make RSA encryption much easier, and to more naturally accommodate other cryptographic primitives.

The ability of the KEM paradigm to easily accommodate cryptographic schemes that are quite different to RSA makes it attractive, and this seems now very much the Right Way to think about hybrid encryption. When NIST announced a competition to design new post-quantum cryptographic algorithms, they explicitly included KEMs as a security goal, and many KEMs were proposed. It’s clear that the KEM-DEM paradigm will be important to the future of public key encryption.

The discussion in this article leaves out a lot of details, such as how to fit public key authenticated encryption into this paradigm (hint), how to achieve forward secrecy, or how to encrypt a message to multiple recipients. These are discussed further in part 2 and part 3.

(*) Other symmetric encryption algorithms are available. I’ll use “AES” in this article to generically refer to symmetric authenticated encryption.

https://neilmadden.blog/2021/01/22/hybrid-encryption-and-the-kem-dem-paradigm/

#hybridEncryption #kemDemParadigm #publicKeyEncryption

Governments are back on their anti-encryption bullshit again.

Between the U.S. Senate’s “EARN IT” Act, the E.U.’s slew of anti-encryption proposals, and Australia’s new anti-encryption law, it’s become clear that the authoritarians in office view online privacy as a threat to their existence.

Normally, when the governments increase their anti-privacy sabre-rattling, technologists start talking more loudly about Tor, Signal, and other privacy technologies (usually only to be drowned out by paranoid people who think Tor and Signal are government backdoors or something stupid; conspiracy theories ruin everything!).

I’m not going to do that.

Instead, I’m going to show you how to add end-to-end encryption to any communication software you’re developing. (Hopefully, I’ll avoid making any bizarre design decisions along the way.)

But first, some important disclaimers:

1. Yes, you should absolutely do this. I don’t care how banal your thing is; if you expect people to use it to communicate with each other, you should make it so that you can never decrypt their communications.
2. You should absolutely NOT bill the thing you’re developing as an alternative to Signal or WhatsApp.
3. The goal of doing this is to increase the amount of end-to-end encryption deployed on the Internet that the service operator cannot decrypt (even if compelled by court order) and make E2EE normalized. The goal is NOT to compete with highly specialized and peer-reviewed privacy technology.
4. I am not a lawyer, I’m some furry who works in cryptography. The contents of this blog post is not legal advice, nor is it endorsed by any company or organization. Ask the EFF for legal questions.

The organization of this blog post is as follows: First, I’ll explain how to encrypt and decrypt data between users, assuming you have a key. Next, I’ll explain how to build an authenticated key exchange and a ratcheting protocol to determine the keys used in the first step. Afterwards, I’ll explore techniques for binding authentication keys to identities and managing trust. Finally, I’ll discuss strategies for making it impractical to ever backdoor your software (and impossible to silently backdoor it), just to piss the creeps and tyrants of the world off even more.

You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing.

(Art by Kyume.)

Preliminaries

Choosing a Cryptography Library

In the examples contained on this page, I will be using the Sodium cryptography library. Specifically, my example code will be written with the Sodium-Plus library for JavaScript, since it strikes a good balance between performance and being cross-platform.

const { SodiumPlus } = require('sodium-plus');(async function() { // Select a backend automatically const sodium = await SodiumPlus.auto(); // Do other stuff here})();

Libsodium is generally the correct choice for developing cryptography features in software, and is available in most programming languages,

If you’re prone to choose a different library, you should consult your cryptographer (and yes, you should have one on your payroll if you’re doing things different) about your design choices.

Threat Modelling

Remember above when I said, “You don’t have to implement the full stack of solutions to protect users, but the further you can afford to go, the safer your users will be from privacy-invasive policing”?

How far you go in implementing the steps outlined on this blog post should be informed by a threat model, not an ad hoc judgment.

For example, if you’re encrypting user data and storing it in the cloud, you probably want to pass the Mud Puddle Test:

1. First, drop your device(s) in a mud puddle.
2. Next, slip in said puddle and crack yourself on the head. When you regain consciousness you’ll be perfectly fine, but won’t for the life of you be able to recall your device passwords or keys.
3. Now try to get your cloud data back.

Did you succeed? If so, you’re screwed. Or to be a bit less dramatic, I should say: your cloud provider has access to your ‘encrypted’ data, as does the government if they want it, as does any rogue employee who knows their way around your provider’s internal policy checks.

Matthew Green describes the Mud Puddle Test, which Apple products definitely don’t pass.

If you must fail the Mud Puddle Test for your users, make sure you’re clear and transparent about this in the documentation for your product or service.

(Art by Swizz.)

I. Symmetric-Key Encryption

The easiest piece of this puzzle is to encrypt data in transit between both ends (thus, satisfying the loosest definition of end-to-end encryption).

At this layer, you already have some kind of symmetric key to use for encrypting data before you send it, and for decrypting it as you receive it.

For example, the following code will encrypt/decrypt strings and return hexadecimal strings with a version prefix.

const VERSION = "v1";/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, key, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(50)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, key, aad ); return plaintext.toString('utf-8');}

Under-the-hood, this is using XChaCha20-Poly1305, which is less sensitive to timing leaks than AES-GCM. However, like AES-GCM, this encryption mode doesn’t provide message- or key-commitment.

If you want key commitment, you should derive two keys from $key using a KDF based on hash functions: One for actual encryption, and the other as a key commitment value.

If you want message commitment, you can use AES-CTR + HMAC-SHA256 or XChaCha20 + BLAKE2b-MAC.

If you want both, ask Taylor Campbell about his BLAKE3-based design.

A modified version of the above code with key-commitment might look like this:

const VERSION = "v2";/** * Derive an encryption key and a commitment hash. * @param {CryptographyKey} key * @param {Uint8Array} nonce * @returns {{encKey: CryptographyKey, commitment: Uint8Array}} */async function deriveKeys(key, nonce) { const encKey = new CryptographyKey(await sodium.crypto_generichash( new Uint8Array([0x01].append(nonce)), key )); const commitment = await sodium.crypto_generichash( new Uint8Array([0x02].append(nonce)), key ); return {encKey, commitment};}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function encryptData(message, key, assocData = null) { const nonce = await sodium.randombytes_buf(24); const aad = JSON.stringify({ 'version': VERSION, 'nonce': await sodium.sodium_bin2hex(nonce), 'extra': assocData }); const {encKey, commitment} = await deriveKeys(key, nonce); const encrypted = await sodium.crypto_aead_xchacha20poly1305_ietf_encrypt( message, nonce, encKey, aad ); return ( VERSION + await sodium.sodium_bin2hex(nonce) + await sodium.sodium_bin2hex(commitment) + await sodium.sodium_bin2hex(encrypted) );}/** * @param {string|Uint8Array} message * @param {Uint8Array} key * @param {string|null} assocData * @returns {string} */async function decryptData(encrypted, key, assocData = null) { const ver = encrypted.slice(0, 2); if (!await sodium.sodium_memcmp(ver, VERSION)) { throw new Error("Incorrect version: " + ver); } const nonce = await sodium.sodium_hex2bin(encrypted.slice(2, 50)); const ciphertext = await sodium.sodium_hex2bin(encrypted.slice(114)); const aad = JSON.stringify({ 'version': ver, 'nonce': encrypted.slice(2, 50), 'extra': assocData }); const storedCommitment = await sodium.sodium_hex2bin(encrypted.slice(50, 114)); const {encKey, commitment} = await deriveKeys(key, nonce); if (!(await sodium.sodium_memcmp(storedCommitment, commitment))) { throw new Error("Incorrect commitment value"); } const plaintext = await sodium.crypto_aead_xchacha20poly1305_ietf_decrypt( ciphertext, nonce, encKey, aad ); return plaintext.toString('utf-8');}

Another design choice you might make is to encode ciphertext with base64 instead of hexadecimal. That doesn’t significantly alter the design here, but it does mean your decoding logic has to accommodate this.

You SHOULD version your ciphertexts, and include this in the AAD provided to your AEAD encryption mode. I used “v1” and “v2” as a version string above, but you can use your software name for that too.

II. Key Agreement

If you’re not familiar with Elliptic Curve Diffie-Hellman or Authenticated Key Exhcanges, the two of the earliest posts on this blog were dedicated to those topics.

Key agreement in libsodium uses Elliptic Curve Diffie-Hellman over Curve25519, or X25519 for short.

There are many schools of thought for extending ECDH into an authenticated key exchange protocol.

We’re going to implement what the Signal Protocol calls X3DH instead of doing some interactive EdDSA + ECDH hybrid, because X3DH provides cryptographic deniability (see this section of the X3DH specification for more information).

For the moment, I’m going to assume a client-server model. That may or may not be appropriate for your design. You can substitute “the server” for “the other participant” in a peer-to-peer configuration.

Head’s up: This section of the blog post is code-heavy.

Update (November 23, 2020): I implemented this design in TypeScript, if you’d like something tangible to work with. I call my library, Rawr X3DH.

X3DH Pre-Key Bundles

Each participant will need to upload an Ed25519 identity key once (which is a detail covered in another section), which will be used to sign bundles of X25519 public keys to use for X3DH.

Your implementation will involve a fair bit of boilerplate, like so:

/** * Generate an X25519 keypair. * * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}} */async function generateKeyPair() { const keypair = await sodium.crypto_box_keypair(); return { secretKey: await sodium.crypto_box_secretkey(keypair), publicKey: await sodium.crypto_box_publickey(keypair) };}/** * Generates some number of X25519 keypairs. * * @param {number} preKeyCount * @returns {{secretKey: X25519SecretKey, publicKey: X25519PublicKey}[]} */async function generateBundle(preKeyCount = 100) { const bundle = []; for (let i = 0; i < preKeyCount; i++) { bundle.push(await generateKeyPair()); } return bundle;}/** * BLAKE2b( len(PK) | PK_0, PK_1, ... PK_n ) * * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function prehashPublicKeysForSigning(publicKeys) { const hashState = await sodium.crypto_generichash_init(); // First, update the state with the number of public keys const pkLen = new Uint8Array([ (publicKeys.length >>> 24) & 0xff, (publicKeys.length >>> 16) & 0xff, (publicKeys.length >>> 8) & 0xff, publicKeys.length & 0xff ]); await sodium.crypto_generichash_update(hashState, pkLen); // Next, update the state with each public key for (let pk of publicKeys) { await sodium.crypto_generichash_update( hashState, pk.getBuffer() ); } // Return the finalized BLAKE2b hash return await sodium.crypto_generichash_final(hashState);}/** * Signs a bundle. Returns the signature. * * @param {Ed25519SecretKey} signingKey * @param {X25519PublicKey[]} publicKeys * @returns {Uint8Array} */async function signBundle(signingKey, publicKeys) { return sodium.crypto_sign_detached( await prehashPublicKeysForSigning(publicKeys), signingKey );}/** * This is just so you can see how verification looks. * * @param {Ed25519PublicKey} verificationKey * @param {X25519PublicKey[]} publicKeys * @param {Uint8Array} signature */async function verifyBundle(verificationKey, publicKeys, signature) { return sodium.crypto_sign_verify_detached( await prehashPublicKeysForSigning(publicKeys), verificationKey, signature );}

This boilerplate exists just so you can do something like this:

/** * Generate some number of X25519 keypairs. * Persist the bundle. * Sign the bundle of publickeys with the Ed25519 secret key. * Return the signed bundle (which can be transmitted to the server.) * * @param {Ed25519SecretKey} signingKey * @param {number} numKeys * @returns {{signature: string, bundle: string[]}} */async function x3dh_pre_key(signingKey, numKeys = 100) { const bundle = await generateBundle(numKeys); const publicKeys = bundle.map(x => x.publicKey); const signature = await signBundle(signingKey, publicKeys); // This is a stub; how you persist it is app-specific: persistBundleNotDefinedHere(signingKey, bundle); // Hex-encode all the public keys const encodedBundle = []; for (let pk of publicKeys) { encodedBundle.push(await sodium.sodium_bin2hex(pk.getBuffer())); } return { 'signature': await sodium.sodium_bin2hex(signature), 'bundle': encodedBundle };}

And then you can drop the output of x3dh_pre_key(secretKey) into a JSON-encoded HTTP request.

In accordance to Signal’s X3DH spec, you want to use x3dh_pre_key(secretKey, 1) to generate the “signed pre-key” bundle and x3dn_pre_key(secretKey, 100) when pushing 100 one-time keys to the server.

X3DH Initiation

This section conforms to the Sending the Initial Message section of the X3DH specification.

When you initiate a conversation, the server should provide you with a bundle containing:

• Your peer’s Identity key (an Ed25519 public key)
• Your peer’s current Signed Pre-Key (an X25519 public key)
• (If any remain unburned) One of your key’s One-Time Keys (an X25519 public key) — and then delete it

If we assume the structure of this response looks like this:

{ "IdentityKey": "...", "SignedPreKey": { "Signature": "..." "PreKey": "..." }, "OneTimeKey": "..." // or NULL}

Then we can write the initiation step of the handshake like so:

/** * Get SK for initializing an X3DH handshake * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} senderKey */async function x3dh_initiate_send_get_sk(r, senderKey) { const identityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey) ); const signedPreKey = new X25519PublicKey( await sodium.sodium_hex2bin(r.SignedPreKey.PreKey) ); const signature = await sodium.sodium_hex2bin(r.SignedPreKey.Signature); // Check signature const valid = await verifyBundle(identityKey, [signedPreKey], signature); if (!valid) { throw new Error("Invalid signature"); } const ephemeral = await generateKeyPair(); const ephSecret = ephemeral.secretKey; const ephPublic = ephemeral.publicKey; // Turn the Ed25519 keys into X25519 keys for X3DH: const senderX = await sodium.crypto_sign_ed25519_sk_to_curve25519(senderKey); const recipientX = await sodium.crypto_sign_ed25519_pk_to_curve25519(identityKey); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(senderX, signedPreKey); const DH2 = await sodium.crypto_scalarmult(ephSecret, recipientX); const DH3 = await sodium.crypto_scalarmult(ephSecret, signedPreKey); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( ephSecret, new X25519PublicKey(await sodium.sodium_hex2bin(r.OneTimeKey)) ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); ephSecret.wipe(); senderX.wipe(); return { IK: identityKey, EK: ephPublic, SK: SK, OTK: r.OneTimeKey // might be NULL };}/** * Initialize an X3DH handshake * * @param {string} recipientIdentity - Some identifier for the user * @param {Ed25519SecretKey} secretKey - Sender's secret key * @param {Ed25519PublicKey} publicKey - Sender's public key * @param {string} message - The initial message to send * @returns {object} */async function x3dh_initiate_send(recipientIdentity, secretKey, publicKey, message) { const r = await get_server_response(recipientIdentity); const {IK, EK, SK, OTK} = await x3dh_initiate_send_get_sk(r, secretKey); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(publicKey.getBuffer()) .concat(IK.getBuffer()) ) ); /* * We're going to set the session key for our recipient to SK. * This might invoke a ratchet. * * Either SK or the output of the ratchet derived from SK * will be returned by getEncryptionKey(). */ await setSessionKey(recipientIdentity, SK); const encrypted = await encryptData( message, await getEncryptionKey(recipientIdentity), assocData ); return { "Sender": my_identity_string, "IdentityKey": await sodium.sodium_bin2hex(publicKey), "EphemeralKey": await sodium.sodium_bin2hex(EK), "OneTimeKey": OTK, "CipherText": encrypted };}

We didn’t define setSessionKey() or getEncryptionKey() above. It will be covered later.

X3DH – Receiving an Initial Message

This section implements the Receiving the Initial Message section of the X3DH Specification.

We’re going to assume the structure of the request looks like this:

{ "Sender": "...", "IdentityKey": "...", "EphemeralKey": "...", "OneTimeKey": "...", "CipherText": "..."}

The code to handle this should look like this:

/** * Handle an X3DH initiation message as a receiver * * @param {object} r -- See previous code block * @param {Ed25519SecretKey} identitySecret * @param {Ed25519PublicKey} identityPublic * @param {Ed25519SecretKey} preKeySecret */async function x3dh_initiate_recv_get_sk( r, identitySecret, identityPublic, preKeySecret) { // Decode strings const senderIdentityKey = new Ed25519PublicKey( await sodium.sodium_hex2bin(r.IdentityKey), ); const ephemeral = new X25519PublicKey( await sodium.sodium_hex2bin(r.EphemeralKey), ); // Ed25519 -> X25519 const senderX = await sodium.crypto_sign_ed25519_pk_to_curve25519(senderIdentityKey); const recipientX = await sodium.crypto_sign_ed25519_sk_to_curve25519(identitySecret); // See the X3DH specification to really understand this part: const DH1 = await sodium.crypto_scalarmult(preKeySecret, senderX); const DH2 = await sodium.crypto_scalarmult(recipientX, ephemeral); const DH3 = await sodium.crypto_scalarmult(preKeySecret, ephemeral); let SK; if (r.OneTimeKey) { let DH4 = await sodium.crypto_scalarmult( await fetchAndWipeOneTimeSecretKey(r.OneTimeKey), ephemeral ); SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) .concat(DH4.getBuffer()) )); DH4.wipe(); } else { SK = kdf(new Uint8Array( [].concat(DH1.getBuffer()) .concat(DH2.getBuffer()) .concat(DH3.getBuffer()) )); } // Wipe keys DH1.wipe(); DH2.wipe(); DH3.wipe(); recipientX.wipe(); return { Sender: r.Sender, SK: SK, IK: senderIdentityKey };}/** * Initiate an X3DH handshake as a recipient * * @param {object} req - Request object * @returns {string} - The initial message */async function x3dh_initiate_recv(req) { const {identitySecret, identityPublic} = await getIdentityKeypair(); const {preKeySecret, preKeyPublic} = await getPreKeyPair(); const {Sender, SK, IK} = await x3dh_initiate_recv_get_sk( req, identitySecret, identityPublic, preKeySecret, preKeyPublic ); const assocData = await sodium.sodium_bin2hex( new Uint8Array( [].concat(IK.getBuffer()) .concat(identityPublic.getBuffer()) ) ); try { await setSessionKey(senderIdentity, SK); return decryptData( req.CipherText, await getEncryptionKey(senderIdentity), assocData ); } catch (e) { await destroySessionKey(senderIdentity); throw e; }}

And with that, you’ve successfully implemented X3DH and symmetric encryption in JavaScript.

We abstracted some of the details away (i.e. kdf(), the transport mechanisms, the session key management mechanisms, and a few others). Some of them will be highly specific to your application, so it doesn’t make a ton of sense to flesh them out.

One thing to keep in mind: According to the X3DH specification, participants should regularly (e.g. weekly) replace their Signed Pre-Key in the server with a fresh one. They should also publish more One-Time Keys when they start to run low.

If you’d like to see a complete reference implementation of X3DH, as I mentioned before, Rawr-X3DH implements it in TypeScript.

Session Key Management

Using X3DH to for every message is inefficient and unnecessary. Even the Signal Protocol doesn’t do that.

Instead, Signal specifies a Double Ratchet protocol that combines a Symmetric-Key Ratchet on subsequent messages, and a Diffie-Hellman-based ratcheting protocol.

Signal even specifies integration guidelines for the Double Ratchet with X3DH.

It’s worth reading through the specification to understand their usages of Key-Derivation Functions (KDFs) and KDF Chains.

Although it is recommended to use HKDF as the Signal protocol specifies, you can strictly speaking use any secure keyed PRF to accomplish the same goal.

What follows is an example of a symmetric KDF chain that uses BLAKE2b with 512-bit digests of the current session key; the leftmost half of the BLAKE2b digest becomes the new session key, while the rightmost half becomes the encryption key.

const SESSION_KEYS = {};/** * Note: In reality you'll want to have two separate sessions: * One for receiving data, one for sending data. * * @param {string} identity * @param {CryptographyKey} key */async function setSessionKey(identity, key) { SESSION_KEYS[identity] = key;}async function getEncryptionKey(identity) { if (!SESSION_KEYS[identity]) { throw new Error("No session key for " + identity"); } const blake2bMac = await sodium.crypto_generichash( SESSION_KEYS[identity], null, 64 ); SESSION_KEYS[identity] = new CryptographyKey(blake2bMac.slice(0, 32)); return new CryptographyKey(blake2bMac.slice(32, 64));}

In the interest of time, a full DHRatchet implementation is left as an exercise to the reader (since it’s mostly a state machine), but using the appropriate functions provided by sodium-plus (crypto_box_keypair(), crypto_scalarmult()) should be relatively straightforward.

Make sure your KDFs use domain separation, as per the Signal Protocol specifications.

Group Key Agreement

The Signal Protocol specified X3DH and the Double Ratchet for securely encrypting information between two parties.

Group conversations are trickier, because you have to be able to encrypt information that multiple recipients can decrypt, add/remove participants to the conversation, etc.

(The same complexity comes with multi-device support for end-to-end encryption.)

The best design I’ve read to date for tackling group key agreement is the IETF Messaging Layer Security RFC draft.

I am not going to implement the entire MLS RFC in this blog post. If you want to support multiple devices or group conversations, you’ll want a complete MLS implementation to work with.

Brief Recap

That was a lot of ground to cover, but we’re not done yet.

(Art by Khia.)

So far we’ve tackled encryption, initial key agreement, and session key management. However, we did not flesh out how Identity Keys (which are signing keys–Ed25519 specifically–rather than Diffie-Hellman keys) are managed. That detail was just sorta hand-waved until now.

So let’s talk about that.

III. Identity Key Management

There’s a meme among technology bloggers to write a post titled “Falsehoods Programmers Believe About _____”.

Fortunately for us, Identity is one of the topics that furries are positioned to understand better than most (due to fursonas): Identities have a many-to-many relationship with Humans.

In an end-to-end encryption protocol, each identity will consist of some identifier (phone number, email address, username and server hostname, etc.) and an Ed25519 keypair (for which the public key will be published).

But how do you know whether or not a given public key is correct for a given identity?

This is where we segue into one of the hard problems in cryptography, where the solutions available are entirely dependent on your threat model: Public Key Infrastructure (PKI).

Some common PKI designs include:

1. Certificate Authorities (CAs) — TLS does this
2. Web-of-Trust (WoT) — The PGP ecosystem does this
3. Trust On First Use (TOFU) — SSH does this
4. Key Transparency / Certificate Transparency (CT) — TLS also does this for ensuring CA-issued certificates are auditable (although it was originally meant to replace Certificate Authorities)

And you can sort of choose-your-own-adventure on this one, depending on what’s most appropriate for the type of software you’re building and who your customers are.

One design I’m particularly fond of is called Gossamer, which is a PKI design without Certificate Authorities, originally designed for making WordPress’s automatic updates more secure (i.e. so every developer can sign their theme and plugin updates).

Since we only need to maintain an up-to-date repository of Ed25519 identity keys for each participant in our end-to-end encryption protocol, this makes Gossamer a suitable starting point.

Gossamer specifies a limited grammar of Actions that can be performed: AppendKey, RevokeKey, AppendUpdate, RevokeUpdate, and AttestUpdate. These actions are signed and published to an append-only cryptographic ledger.

I would propose a sixth action: AttestKey, so you can have WoT-like assurances and key-signing parties. (If nothing else, you should be able to attest that the identity keys of other cryptographic ledgers in the network are authentic at a point in time.)

IV. Backdoor Resistance

In the previous section, I proposed the use of Gossamer as a PKI for Identity Keys. This would provide Ed25519 keypairs for use with X3DH and the Double Ratchet, which would in turn provide session keys to use for symmetric authenticated encryption.

If you’ve implemented everything preceding this section, you have a full-stack end-to-end encryption protocol. But let’s make intelligence agencies and surveillance capitalists even more mad by making it impractical to backdoor our software (and impossible to silently backdoor it).

How do we pull that off?

You want Binary Transparency.

For us, the implementation is simple: Use Gossamer as it was originally intended (i.e. to secure your software distribution channels).

Gossamer provides up-to-date verification keys and a commitment to a cryptographic ledger of every software update. You can learn more about its inspiration here.

It isn’t enough to merely use Gossamer to manage keys and update signatures. You need independent third parties to use the AttestUpdate action to assert one or more of the following:

1. That builds are reproducible from the source code.
2. That they have reviewed the source code and found no evidence of backdoors or exploitable vulnerabilities.

(And then you should let your users decide which of these independent third parties they trust to vet software updates.)

Closing Remarks

The U.S. Government cries and moans a lot about “criminals going dark” and wonders a lot about how to solve the “going dark problem”.

If more software developers implement end-to-end encryption in their communications software, then maybe one day they won’t be able to use dragnet surveillance to spy on citizens and they’ll be forced to do actual detective work to solve actual crimes.

Y’know, like their job description actually entails?

Let’s normalize end-to-end encryption. Let’s normalize backdoor-resistant software distribution.

Let’s collectively tell the intelligence community in every sophisticated nation state the one word they don’t hear often enough:

Especially if you’re a furry. Because we improve everything! :3

Questions You Might Have

What About Private Contact Discovery?

That’s one of the major reasons why the thing we’re building isn’t meant to compete with Signal (and it MUST NOT be advertised as such):

Signal is a privacy tool, and their servers have no way of identifying who can contact who.

What we’ve built here isn’t a complete privacy solution, it’s only providing end-to-end encryption (and possibly making NSA employees cry at their desk).

Does This Design Work with Federation?

Yes. Each identifier string can be [username] at [hostname].

What About Network Metadata?

If you want anonymity, you want to use Tor.

Why Are You Using Ed25519 Keys for X3DH?

If you only read the key agreement section of this blog post and the fact that I’m passing around Ed25519 public keys seems weird, you might have missed the identity section of this blog post where I suggested piggybacking on another protocol called Gossamer to handle the distribution of Ed25519 public keys. (Gossamer is also beneficial for backdoor resistance in software update distribution, as described in the subsequent section.)

Furthermore, we’re actually using birationally equivalent X25519 keys derived from the Ed25519 keypair for the X3DH step. This is a deviation from what Signal does (using X25519 keys everywhere, then inventing an EdDSA variant to support their usage).

const publicKeyX = await sodium.crypto_sign_ed25519_pk_to_curve25519(foxPublicKey);const secretKeyX = await sodium.crypto_sign_ed25519_sk_to_curve25519(wolfSecretKey);

(Using fox/wolf instead of Alice/Bob, because it’s cuter.)

This design pattern has a few advantages:

1. It makes Gossamer integration seamless, which means you can use Ed25519 for identities and still have a deniable X3DH handshake for 1:1 conversations while implementing the rest of the designs proposed.
2. This approach to X3DH can be implemented entirely with libsodium functions, without forcing you to write your own cryptography implementations (i.e. for XEdDSA).

The only disadvantages I’m aware of are:

1. It deviates from Signal’s core design in a subtle way that means you don’t get to claim the exact same advantages Signal does when it comes to peer review.
2. Some cryptographers are distrustful of the use of birationally equivalent X25519 keys from Ed25519 keys (although there isn’t a vulnerability any of them have been able to point me to that doesn’t involve torsion groups–which libsodium’s implementation already avoids).

If these concerns are valid enough to decide against my implementation above, I invite you to talk with cryptographers about your concerns and then propose alternatives.

Has Any of This Been Implemented Already?

You can find implementations for the designs discussed on this blog post below:

• Rawr-X3DH implements X3DH in TypeScript (added 2020-11-23)

I will update this section of the blog post as implementations surface.

https://soatok.blog/2020/11/14/going-bark-a-furrys-guide-to-end-to-end-encryption/

#authenticatedEncryption #authenticatedKeyExchange #crypto #cryptography #encryption #endToEndEncryption #libsodium #OnlinePrivacy #privacy #SecurityGuidance #symmetricEncryption

Dhole Moments

2020-10-28 15:44:22

Zoom recently announced that they were going to make end-to-end encryption available to all of their users–not just customers.

https://twitter.com/zoom_us/status/1320760108343652352

This is a good move, especially for people living in countries with inept leadership that failed to address the COVID-19 pandemic and therefore need to conduct their work and schooling remotely through software like Zoom. I enthusiastically applaud them for making this change.

End-to-end encryption, on by default, is a huge win for everyone who uses Zoom. (Art by Khia.)

The end-to-end encryption capability arrives on the heels of their acquisition of Keybase in earlier this year. Hiring a team of security experts and cryptography engineers seems like a good move overall.

Upon hearing this news, I decided to be a good neighbor and take a look at their source code, with the reasoning, “If so many people’s privacy is going to be dependent on Zoom’s security, I might as well make sure they’re not doing something ridiculously bad.”

Except I couldn’t find their source code anywhere online. But they did publish a white paper on Github…

(Art by Khia.)

Disclaimers

What follows is the opinion of some guy on the Internet with a fursona–so whether or not you choose to take it seriously should be informed by this context. It is not the opinion of anyone’s employer, nor is it endorsed by Zoom, etc. Tell your lawyers to calm their nips.

More importantly, I’m not here to hate on Zoom for doing a good thing, nor on the security experts that worked hard on making Zoom better for their users. The responsibility of security professionals is to the users, after all.

Also, these aren’t zero-days, so don’t try to lecture me about “responsible” disclosure. (That term is also problematic, by the way.)

Got it? Good. Let’s move on.

(Art by Swizz.)

Bizarre Design Choices in Version 2.3 of Zoom’s E2E White Paper

Note: I’ve altered the screenshots to be white text on a black background, since my blog’s color scheme is darker than a typical academic PDF. You can find the source here.

Cryptographic Algorithms

It’s a little weird that they’re calculating a signature over SHA256(Context) || SHA256(M), considering Ed25519 uses SHA512 internally.

It would make just as much sense to sign Context || M directly–or, if pre-hashing large streams is needed, SHA512(Context || M).

At the top of this section, it says it uses libsodium’s crypto_box interface. But then they go onto… not actually use it.

Instead, they wrote their own protocol using HKDF, two SHA256 hashes, and XChaCha20-Poly1305.

While secure, this isn’t really using the crypto_box interface.

The only part of the libsodium interface that’s being used is [url=https://github.com/jedisct1/libsodium/blob/927dfe8e2eaa86160d3ba12a7e3258fbc322909c/src/libsodium/crypto_box/curve25519xsalsa20poly1305/box_curve25519xsalsa20poly1305.c#L35-L46]crypto_box_beforenm()[/url], which could easily have been a call to crypto_scalarmult()instead (since they’re passing the output of the scalar multiplication to HKDF anyway).

(Art by Riley.)

Also, the SHA256(a) || SHA256(b) pattern returns. Zoom’s engineers must love SHA256 for some reason.

This time, it’s in the additional associated data for the XChaCha20-Poly1305.

Binding the ciphertext and the signature to the same context string is a sensible thing to do, it’s just the concatenation of SHA256 hashes is a bit weird when SHA512 exists.

Meeting Leader Security Code

Here we see Zoom using the a SHA256 of a constant string (“Zoombase-1-ClientOnly-MAC-SecurityCode“) in a construction that tries but fails to be HMAC.

And then they concatenate it with the SHA256 hash of the public key (which is already a 256-bit value), and then they hash the whole thing again.

It’s redundant SHA256 all the way down. The redundancy of “MAC” and “SecurityCode” in their constant string is, at least, consistent with the rest of their design philosophy.

It would be a real shame if double-hashing carried the risk of invalidating security proofs, or if the security proof for HMAC required a high Hamming distance of padding constants and this design decision also later saved HMAC from related-key attacks.

Hiding Personal Details

Wait, you’re telling me Zoom was aware of HMAC’s existence this whole time?

I give up!

Enough Pointless Dunking, What’s the Takeaway?

None of the design decisions Zoom made that I’ve criticized here are security vulnerabilities, but they do demonstrate an early lack of cryptography expertise in their product design.

After all, the weirdness is almost entirely contained in section 3 of their white paper, which describes the “Phase I” of their rollout. So what I’ve pointed out here appears to be mostly legacy cruft that wasn’t risky enough to bother changing in their final design.

The rest of their paper is pretty straightforward and pleasant to read. Their design makes sense in general, and each phase includes an “Areas to Improve” section.

All in all, if you’re worried about the security of Zoom’s E2EE feature, the only thing they can really do better is to publish the source code (and link to it from the whitepaper repository for ease-of-discovery) for this feature so independent experts can publicly review it.

However, they seem to be getting a lot of mileage out of the experts on their payroll, so I wouldn’t count on that happening.

https://soatok.blog/2020/10/28/bizarre-design-choices-in-zooms-end-to-end-encryption/

#encryption #endToEndEncryption #zoom