Imagine you’re a software developer, and you need to authenticate users based on a username and password.

If you’re well-read on the industry standard best practices, you’ll probably elect to use something like bcrypt, scrypt, Argon2id, or PBKDF2. (If you thought to use something else, you’re almost certainly doing it wrong.)

Let’s say, due to technical constraints, that you’re forced to select PBKDF2 out of the above options, but you’re able to use a suitable hash function (i.e. SHA-256 or SHA-512, instead of SHA-1).

Every password is hashed with a unique 256-bit salt, generated from a secure random generator, and has an iteration count in excess of 80,000 (for SHA-512) or 100,000 (for SHA-256). So far, so good.

(Art by Khia.)

Let’s also say your users’ passwords are long, randomly-generated strings. This can mean either you’re building a community of password manager aficionados, or your users are actually software bots with API keys.

Every user’s password is, therefore, always a 256 character string of random hexadecimal characters.

Two sprints before your big launch, your boss calls you and says, “Due to arcane legal compliance reasons, we need to be able to detect duplicate passwords. It needs to be fast.”

You might might think, “That sounds like a hard problem to solve.”

Your boss insists, “The passwords are all too long and too high-entropy to reliably attacked, even when we’re using a fast hash, so we should be able to get by with a simple hash function for deduplication purposes.”

So you change your code to look like this:

<?phpuse ParagonIE\EasyDB\EasyDB;use MyApp\Security\PasswordHash;class Authentication { private EasyDB $db; public function __construct(EasyDB $db) { $this->db = $db; $this->pwhash = new PasswordHash('sha256'); } public function signUp(string $username, string $password) { // New: $hashed = hash('sha256', $password); if ($db->exists( "SELECT count(id) FROM users WHERE pw_dedupe = ?", $hashed )) { throw new Exception( "You cannot use the same username or password as another user." ); } // Original: if ($db->exists( "SELECT count(id) FROM users WHERE username = ?", $username )) { throw new Exception( "You cannot use the same username or password as another user." ); } $this->db->insert('users', [ 'username' => $username, 'pwhash' => $this->pwhash->hash($password), // Also new: 'pw_dedupe' => $hashed ]); } public function logIn(string $username, string $password): int { // This is unchanged: $user = $this->db->row("SELECT * FROM users WHERE username = ?", $username); if (empty($user)) { throw new Exception("Security Error: No user"); } if ($this->pwhash->verify($password, $user['pwhash'])) { throw new Exception("Security Error: Incorrect password"); } return (int) $user['id']; }}

Surely, this won’t completely undermine the security of the password hashing algorithm?

Is this a face that would mislead you? (Art by Khia.)

Three years later, a bored hacker discovers a read-only SQL injection vulnerability, and is immediately able to impersonate any user in your application.

What could have possibly gone wrong?

Cryptography Bugs Are Subtle

https://twitter.com/SwiftOnSecurity/status/832058185049579524

In order to understand what went wrong in our hypothetical scenario, you have to kinda know what’s under the hood in the monstrosity that our hypothetical developer slapped together.

PBKDF2

PBKDF2 stands for Password-Based Key Derivation Function #2. If you’re wondering where PBKDF1 went, I discussed its vulnerability in another blog post about the fun we can have with hash functions.

PBKDF2 is supposed to be instantiated with some kind of pseudo-random function, but it’s almost always HMAC with some hash function (SHA-1, SHA-256, and SHA-512 are common).

So let’s take a look at HMAC.

HMAC

HMAC is a Message Authentication Code algorithm based on Hash functions. Its definition looks like this:

Source: Wikipedia

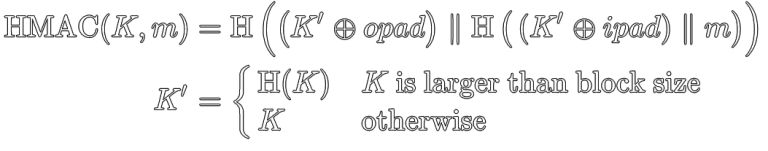
For the purposes of this discussion, we only care about the definition of K’.

If your key (K) is larger than the block size of the hash function, it gets pre-hashed with that hash function. If it’s less than or equal to the block size of the hash function, it doesn’t.

So, what is PBKDF2 doing with K?

How PBKDF2 Uses HMAC

The RFCs that define PBKDF2 aren’t super helpful here, but one needs only look at a reference implementation to see what’s happening.

// first iteration$last = $xorsum = hash_hmac($algorithm, $last, $password, true);// perform the other $count - 1 iterationsfor ($j = 1; $j < $count; $j++) {$xorsum ^= ($last = hash_hmac($algorithm, $last, $password, true));}$output .= $xorsum;

If you aren’t fluent in PHP, it’s using the previous round’s output as the message (m in the HMAC definition) and the password as the key (K).

Which means if your password is larger than the block size of the hash function used by HMAC (which is used by PBKDF2 under the hood), it will be pre-hashed.

The Dumbest Exploit Code

Okay, with all of that in mind, here’s how you can bypass the authentication of the above login script.

$httpClient->loginAs( $user['username'], hex2bin($user['pw_dedupe']));

Since K’ = H(K) when Length(K) > BlockSize(H), you can just take the pre-calculated hash of the user’s password and use that as the password (although not hex-encoded), and it will validate. (Demo.)

This is probably how you feel right now, if you didn’t already know about this.
(Art by Khia.)

Above, when HMAC defined K’, it included a variant in its definition. Adding variants to hash function is a dumb way to introduce the risk of collisions. (See also: Trivial Collisions in IOTA’s Kerl hash function.)

Also, some PBKDF2 implementations that mishandle the pre-hashing of K, which can lead to denial-of-service attacks. Fun stuff, right?

Some Dumb Yet Effective Mitigations

Here are a few ways the hypothetical developer could have narrowly avoided this security risk:

• Use a different hash function for PBKDF2 and the deduplication check.
  
  • e.g. PBKDF2-SHA256 and SHA512 would be impervious

  
  

• Always pre-hashing the password before passing it to PBKDF2.
  
  • Our exploit attempt will effectively be double-hashed, and will not succeed.

  
  

• Use HMAC instead of a bare hash for the deduplication. With a hard-coded, constant key.
• Prefix the password with a distinct domain separation constant in each usage.
• Truncate the hash function, treating it as a Bloom filter.
• Some or all of the above.
• Push back on implementing this stupid feature to begin with.

Subtle problems often (but not always) call for subtle solutions.

Password Security Advice, Revisited

One dumb mitigation technique I didn’t include above is, “Using passwords shorter than the block size of the hash function.” The information security industry almost unanimously agrees that longer passwords are better than short ones (assuming both have the same distribution of possible characters at each position in the string, and are chosen randomly).

But here, we have a clear-cut example where having a longer password actually decreased security by allowing a trivial authentication bypass. Passwords with a length less than or equal to the block size of the hash function would not be vulnerable to the attack.

For reference, if you ever wanted to implement this control (assuming ASCII characters, where 1 character = 1 byte):

• 64-character passwords would be the upper limit for MD5, SHA-1, SHA-224, and SHA-256.
• 128-character passwords would be the upper limit for SHA-384 and SHA-512.
• (Since the above example used 256-character passwords, it always overflows.)

But really, one of the other mitigation techniques would be better. Limiting the input length is just a band-aid.

Another Non-Obvious Footgun

Converse to the block size of the hash function, the output size of the hash function also affects the security of PBKDF2, because each output is calculated sequentially. If you request more bytes out of a PBKDF2 function than the hash function outputs, it will have to work at least twice as hard.

This means that, while a legitimate user has to calculate the entire byte stream from PBKDF2, an attacker can just target the first N bytes (20 for SHA-1, 32 for SHA-256, 64 for SHA-512) of the raw hash output and attack that instead of doing all the work.

Is Cryptography Hard?

I’ve fielded a lot of questions in the past few weeks, and consequently overheard commentary from folks insisting that cryptography is a hard discipline and therefore only the smartest should study it. I disagree with that, but not for the reason that most will expect.

Many of the people reading this page will tell me, “This is such a dumb and obvious design flaw. Nobody would ship that code in production,” because they’re clever or informed enough to avoid disaster.

Yet, we still regularly hear about JWT alg=none vulnerabilities. And Johnny still still can’t encrypt. So cryptography surely can’t be easy.

Art by Riley.

Real-world cryptographic work is cognitively demanding. It becomes increasingly mathematically intensive the deeper you study, and nobody knows how to name things that non-cryptographers can understand. (Does anyone intuitively understand what a public key is outside of our field?)

In my opinion, cryptography is certainly challenging and widely misunderstood. There are a lot of subtle ways for secure building blocks to be stitched together insecurely. And today, it’s certainly a hard subject for most people to learn.

However, I don’t think its hardness is unavoidable.

Descending the Mohs Scale

There is a lot of gatekeeping in the information security community. (Maybe we should expect that to happen when people spend too many hours staring at firewall rules?)

“Don’t roll your own crypto” is something you hear a lot more often from software engineers and network security professionals than bona fide cryptographers.

Needless gatekeeping does the cryptographic community a severe disservice. I’m not the first to suggest that, either.

From what I’ve seen, far too many people feel discouraged from learning about cryptography, thinking they aren’t smart enough for it. It would seem A Mathematician’s Lament has an echo.

If it can be said that cryptography is hard today, then that has more to do with incomplete documentation and substandard education resources available for free online than some inherent mystical quality of our discipline that only the christened few can ever hope to master.

Cryptographers and security engineers that work in cryptography need more developers to play in our sandbox. We need more usability experts to discuss improvements to our designs and protocols to make them harder to misuse. We also need science communication experts and a legal strategy to stop idiotic politicians from trying to foolishly ban encryption.

So if you’re reading my blog, wondering, “Will I ever be smart enough to understand this crap?” the answer is probably “Yes!” It might not be easy, but with any luck, it’ll be easier than it was for the forerunners in our field.

If a random furry can grok these topics, what’s stopping you? This dhole believes in you.
(Art by Khia.)

I have one request, though: If you’re thinking of learning cryptography, please blog about your journey (even if you’re not a furry). You may end up filling in a pothole that would otherwise have tripped someone else up.

https://soatok.blog/2020/11/27/the-subtle-hazards-of-real-world-cryptography/

#computerSecurity #cryptographicHashFunction #cryptography #dumbExploit #HMAC #infosec #passwordHashing #PBKDF2 #SecurityGuidance

Dhole Moments

2020-05-05 12:00:22

There are several different methods for securely hashing a password server-side for storage and future authentication. The most common one (a.k.a. the one that FIPS allows you to use, if compliance matters for you) is called PBKDF2. It stands for Password-Based Key Derivation Function #2.

Why #2? It’s got nothing to do with pencils. There was, in fact, a PBKDF1! But PBKDF1 was fatally insecure in a way I find very interesting. This StackOverflow answer is a great explainer on the difference between the two.

Very Hand-Wavy Description of a Hash Function

Let’s defined a hash function as any one-way transformation of some arbitrary-length string () to a fixed-length, deterministic, pseudo-random output.

Note: When in doubt, I err on the side of being easily understood by non-experts over pedantic precision. (Art by Swizz)

For example, this is a dumb hash function (uses SipHash-2-4 with a constant key):

function dumb_hash(string $arbitrary, bool $raw_binary = false): string{ $h = sodium_crypto_shorthash($arbitrary, 'SoatokDreamseekr'); if ($raw_binary) { return $h; } return sodium_bin2hex($h);}

You can see the output of this function with some sample inputs here.

Properties of Hash Functions

A hash function is considered secure if it has the following properties:

1. Pre-image resistance. Given , it should be difficult to find .
2. Second pre-image resistance. Given , it should be difficult to find such that
3. Collision resistance. It should be difficult to find any arbitrary pair of messages () such that

That last property, collision resistance, is guaranteed up to the Birthday Bound of the hash function. For a hash function with a 256-bit output, you will expect to need on average trial messages to find a collision.

If you’re confused about the difference between collision resistance and second pre-image resistance:

Collision resistance is about finding any two messages that produce the same hash, but you don’t care what the hash is as long as two distinct but known messages produce it.

On the other paw, second pre-image resistance is about finding a second message that produces a given hash.

Exploring PBKDF1’s Insecurity

If you recall, hash functions map an arbitrary-length string to a fixed-length string. If your input size is larger than your output size, collisions are inevitable (albeit computationally infeasible for hash functions such as SHA-256).

But what if your input size is equal to your output size, because you’re taking the output of a hash function and feeding it directly back into the same hash function?

Then, as explained here, you get an depletion of the possible outputs with each successive iteration.

But what does that look like?

Without running the experiments on a given hash function, there are two possibilities that come to mind:

1. Convergence. This is when will, for two arbitrary messages and a sufficient number of iterations, converge on a single hash output.
2. Cycles. This is when for some integer .

The most interesting result would be a quine, which is a cycle where (that is to say, ).

The least interesting result would be for random inputs to converge into large cycles e.g. cycles of size for a 256-bit hash function.

I calculated this lazily as the birthday bound of the birthday bound (so basically the 4th root, which for is ).

Update: According to this 1960 paper, the average time to cycle is , and cycle length should be , which means for a 256-bit hash you should expect a cycle after about or about 128 bits, and the average cycle length will be about . Thanks Riastradh for the corrections.

Conjecture: I would expect secure cryptographic hash functions in use today (e.g. SHA-256) to lean towards the least interesting output.

An Experiment Design

Since I don’t have an immense amount of cheap cloud computing at my disposal to run this experiments on a real hash function, I’m going to cheat a little and use my constant-key SipHash code from earlier in this post. In future work, cryptographers may find studying real hash functions (e.g. SHA-256) worthwhile.

Given that SipHash is a keyed pseudo-random function with an output size of 64 bits, my dumb hash function can be treated as a 64-bit hash function.

This means that you should expect your first collision (with 50% probability) after only trial hashes. This is cheap enough to try on a typical laptop.

Here’s a simple experiment for convergence:

1. Generate two random strings .
2. Set .
3. Iterate until .

You can get the source code to run this trivial experiment here.

Clone the git repository, run composer install, and then php bin/experiment.php. Note that this may need to run for a very long time before you get a result.

If you get a result, you’ve found a convergence.

If the loop doesn’t terminate even after 2^64 iterations, you’ve definitely found a cycle. (Actually detecting a cycle and analyzing its length would require a lot of memory, and my simple PHP script isn’t suitable for this effort.)

“What do you mean I don’t have a petabyte of RAM at my disposal?”

What Does This Actually Tell Us?

The obvious lesson: Don’t design key derivation functions like PBKDF1.

But beyond that, unless you can find a hash function that reliably converges or produces short cycles (, for an n-bit hash function), not much. (This is just for fun, after all!)

Definitely fun to think about though! (Art by circuitslime)

If, however, a hash function is discovered to produce interesting results, this may indicate that the chosen hash function’s internal design is exploitable in some subtle ways that, upon further study, may lead to better cryptanalysis techniques. Especially if a hash quine is discovered.

(Header art by Khia)

https://soatok.blog/2020/05/05/putting-the-fun-in-hash-function/

#crypto #cryptography #hashFunction #SipHash