Search
Items tagged with: cryptography
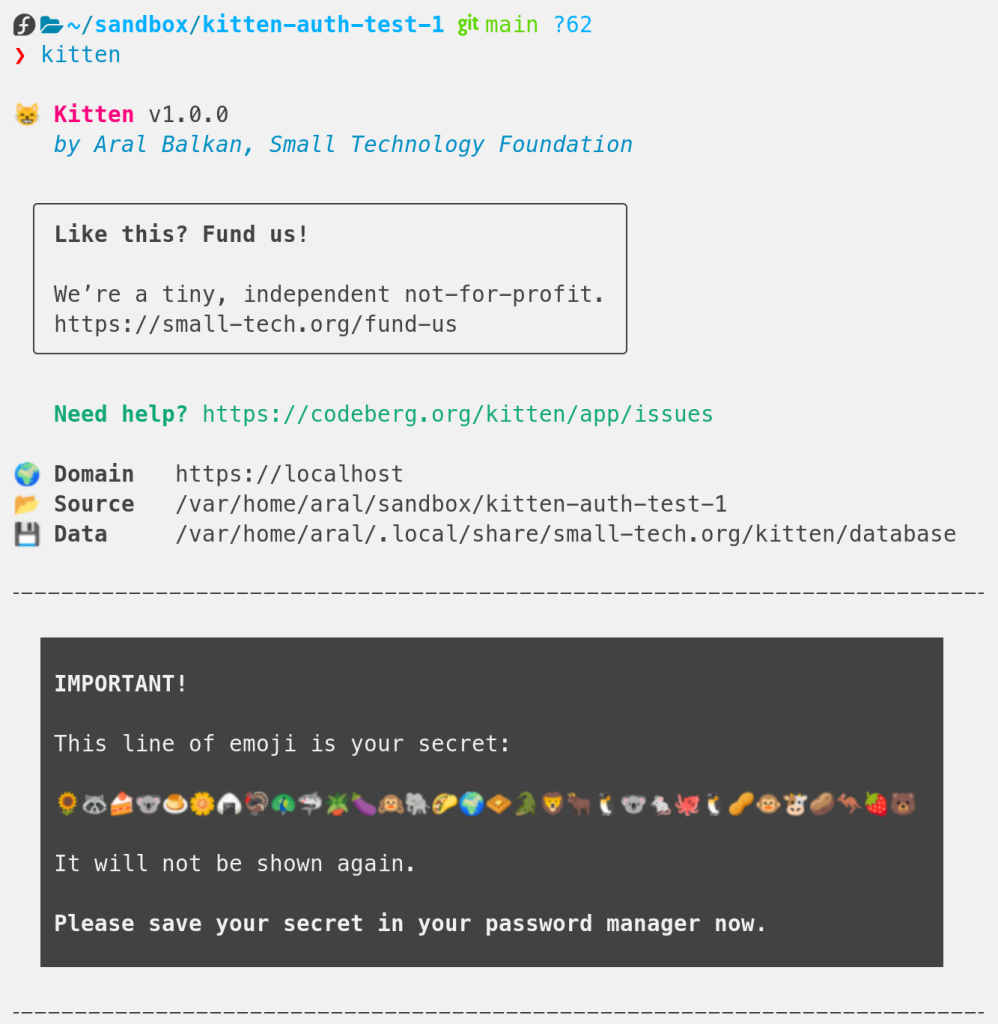
Wait, what?… you don’t mean that your all-important secret for your Small Web site is going to be… A STRING OF EMOJI?!*
(Why yes, yes it is…) :awesome:
* Or, if you want to take all the fun out of it, a base256 encoding of your ed25519 private key that is purposefully impractical to write down somewhere or type in so you’ll be forced to practice good security hygiene and store it in your password manager.
#design #security #privacy #cryptography #kitten #SmallWeb #SmallTech
(Why yes, yes it is…) :awesome:
* Or, if you want to take all the fun out of it, a base256 encoding of your ed25519 private key that is purposefully impractical to write down somewhere or type in so you’ll be forced to practice good security hygiene and store it in your password manager.
#design #security #privacy #cryptography #kitten #SmallWeb #SmallTech