Search
Items tagged with: P256
Earlier this year, Cendyne published A Deep Dive into Ed25519 Signatures, which covered some of the different types of digital signature algorithms, but mostly delved into the Ed25519 algorithm. Truth in advertising.
This got me thinking, “Why isn’t there a better comparison of different elliptic curve signature algorithms available online?”

Most people just defer to SafeCurves, but it’s a little dated: We have complete addition formulas for Weierstrass curves now, but SafeCurves doesn’t reflect that.
For the purpose of simplicity, I’m not going to focus on a general treatment of Elliptic Curve Cryptography (ECC), which includes pairing-based cryptography, Elliptic-Curve Diffie-Hellman, and (arguably) isogeny cryptography.
Instead, I’m going to focus entirely on elliptic curve digital signature algorithms.
Note: The content of this post is a bit lower-level than most programmers ever need to be concerned with. If you’re a programmer and interested in learning cryptography, start here. If you’re looking for library recommendations, libsodium is a good safe default.
Compliance Rules Everything Around Me
If you have to meet some arbitrary compliance requirements (i.e. FIPS 140-3, CNSA, etc.), your decision is already made for you, and you shouldn’t waste your time reading blogs like this that will only get your hopes up about the options available to you.
Choose the option your compliance officer demands, and hope it’s good enough.

Art: LvJ
Elliptic Curves for Signature Algorithms
Let’s start with the same curve Cendyne analyzed: Ed25519.
Ed25519 (EdDSA, Curve25519)
Ed25519 is one of the two digital signature algorithms today that use the EdDSA algorithm framework. The other is Ed448, which targets a higher security level (224-bit vs 128-bit) but is also slower and uses SHAKE256 (which is overkill and not great for performance).
Ed25519 is a safe default choice for most applications where a digital signature is appropriate, for many reasons:
- Ed25519 uses deterministic nonces, which means you’re severely unlikely to ever reproduce the Sony ECDSA k-reuse bug in your system.
The deterministic nonce is calculated from the SHA512 hash of the secret key and message. Two invocations tocrypto_sign_ed25519()with the same message and secret key will produce the same signature, but the intermediate nonce value is never revealed to an attacker. - Ed25519 includes the public key in the data hashed to produce the signature (more specifically s from the (R,s) pair). This offers a property that ECDSA lacks: Exclusive Ownership. I’ve written about this property before.
Without Exclusive Ownership, it’s possible to create a single signature value that’s valid for multiple different (message, public key) pairs.
Years ago, there would have an additional list item: Ed25519 uses Edward Curves, which have complete addition formulas and are therefore safer to implement in constant-time than Weierstrass curves (i.e. the NIST curves). However, we now have complete addition formulas for Weierstrass curves, so this has become a moot point (assuming your implementation uses complete addition formulas).
Ed25519 targets the 128-bit security level.
Why Not Use Ed25519?
There is one minor pitfall of Ed25519 that makes it unsuitable for esoteric uses (say, Ring Signature Schemes or zero-knowledge proofs): Ed25519 is not a prime-order group; it has a cofactor h = 8. This detail famously created a double-spend vulnerability in all CryptoNote-based cryptocurrencies (including Monero).
For systems that want the security of Ed25519 and its various well-studied implementations, but still need a prime-order group for their protocol, cryptographers have developed the Ristretto Group to meet your needs.
If you’re working on embedded systems, the determinism inherent to EdDSA might be undesirable due to the possibility of fault attacks. You can use a hedged variant of Ed25519 to mitigate this risk.
Additionally, Ed25519 is not approved for many government applications, although it did make the latest draft revision of FIPS 186 in 2019. If you care about compliance (see above), you cannot use Ed25519. Yet.

Guidance for Ed25519
Unless legally prohibited, Ed25519 should be your default choice, unless you need a prime-order group. In that case, build your desired protocol atop Ristretto255.
If you’re not sure if you need a prime-order group, you probably don’t. It’s a specialized requirement for uncommon use cases (ring signatures, password authenticated key exchange protocols, zero-knowledge proofs, etc.).

The Bitcoin Curve (ECDSA, secp256k1)
Secp256k1 is a Koblitz curve, which is a special case of Weierstrass curves that are more performant when used in binary fields, of the form, 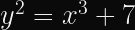
There is no specified reason why Bitcoin chose secp256k1 over another elliptic curve at the time of its inception, but we can speculate:
The author was a pseudonymous contributor to the Metzdowd mailing list for cypherpunks, and probably didn’t trust the NIST curves. Since Ed25519 didn’t exist at the time, the only obvious choice for a hipster elliptic curve parameter selection was to rely on the SECG recommendations, which specify the NIST and Koblitz curves. If you cross the NIST curves off the list, only the Koblitz curves remained.
Therefore, the selection of secp256k1 is likely an artefact of computer history and not a compelling reason to select secp256k1 in new designs. Please look elsewhere.

Secp256k1 targets the 128-bit security level.
Guidance for secp256k1
Don’t bother, there are better options. (i.e. Ed25519)
If you’re writing software for a cryptocurrency-related project, and you feel compelled to use secp256k1 for the sake of reducing your code footprint, please strongly consider the option of burning everything to the proverbial ground.

Art: Swizz
Cryptocurrency Aside, Why Avoid Secp256k1?
As we noted above, secp256k1 isn’t widely used outside of cryptocurrency.
As a direct consequence of this (as we’ll discuss in the NIST P-256 section), most cryptography libraries don’t offer optimized, side-channel-resistant implementations of secp256k1; even if they do offer optimized implementations of NIST P-256.
(Meanwhile, Ed25519 is designed to be side-channel and misuse-resistant, partly due to its Schnorr construction and constant-time ladder for scalar multiplication, so any library that implements Ed25519 is overwhelmingly likely to be constant-time.)
Therefore, any secp256k1 library for most programming languages that isn’t an FFI wrapper for libsecp256k1 will have worse performance than the other 256-bit curves.
https://twitter.com/bascule/status/1320183684935290882
Additionally, secp256k1 implementations are often a source of exploitable side-channels that permit attackers to pilfer your secret keys.
The previously linked article was about BouncyCastle’s implementation (which covers Java and .NET), but there’s still plenty of secp256k1 implementations that don’t FFI libsecp256k1.
From a quick Google Search:
- Python (uses EEA rather than Binary GCD for modular inverse)
- Go (uses Numbers, which weren’t designed for cryptography)
- PHP (uses GMP, which isn’t constant-time)
- JavaScript (calls here, which uses bn.js, which isn’t constant-time)
If you’re using secp256k1, and you’re not basing your choice on cybercash-interop, you’re playing with fire at the implementation and ecosystem levels–even if there are no security problems with the Koblitz curve itself.
You are much better off choosing any different curve than secp256k1 if you don’t have a Bitcoin/Ethereum/etc. interoperability requirement.

Art: LvJ
NIST P-256 (ECDSA, secp256r1)
NIST P-256 is the go-to curve to use with ECDSA in the modern era. Unlike Ed25519, P-256 uses a prime-order group, and is an approved algorithm to use in FIPS-validated modules.
Most cryptography libraries offer optimized assembly implementations of NIST P-256, which makes it less likely that your signing operations will leak timing information or become a significant performance bottleneck.
P-256 targets the 128-bit security level.
Why Not Use P-256?
Once upon a time, P-256 was riskier than Ed25519 (for signatures) and X25519 (for Diffie-Hellman), due to the incomplete addition formulas that led to timing-leaky implementations.
If you’re running old software, you may still be vulnerable to timing attacks that can recover your ECDSA secret key. However, there is a good chance that you’re on a modern and secure implementation in 2022, especially if you’re outsourcing this to OpenSSL or its derivatives.
ECDSA requires a secure randomness source to sign data. If you don’t have one available, and you sign anything, you’re coughing up your secret key to any attacker capable of observing multiple signatures.
Guidance for P-256
P-256 is an acceptable choice, especially if you’re forced to cope with FIPS and/or the CNSA suite requirements when using cryptography.
Of course, if you can get away with Ed25519, use Ed25519 instead.
If you use P-256, make sure you’re using it with SHA-256. Some implementations may default to something weaker (e.g. SHA-1).
If you’re also going to be performing ECDH with P-256, make sure you use compressed points. There used to be a patent; it died in 2018.
If you can afford it, make sure you use deterministic ECDSA (RFC 6979) or hedged signatures (if fault attacks are relevant to your threat model).

NIST P-384 (ECDSA, secp384r1)
NIST P-384 has a larger field than the curves we’ve previously examined, which allows P-384 to target the 192-bit security level. That’s the primary reason why anyone would choose P-384.
Naturally, elliptic curve security is more complicated than merely security against the Elliptic Curve Discrete Logarithm Problem (ECDLP).
P-384 is most often paired with SHA-384, which is the most widely used flavor of the SHA-2 family hash functions that isn’t susceptible to length-extension attacks. (There are also truncated SHA-512 variants specified later, but that’s also what SHA-384 is under-the-hood.)
If you’re aiming to build a “secure-by-default” tool for a system that the US government might one day become a customer of, with minimal cryptographic primitive choice, using NIST P-384 with SHA-384 makes for a reasonably minimalistic bundle.
Why Not Use P-384?
Unlike P-256, most P-384 implementations don’t use constant-time, optimized, and/or formally verified assembly code. (Notable counter-examples: AWS-LC and Go x/crypto.)
Like P-256, P-384 also requires a secure randomness source to sign data. If you aren’t providing one, expect your signing key to end up on fail0verflow one day.
Guidance for P-384
If you use P-384, make sure you’re using it with SHA-384.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

NIST P-521 (ECDSA, secp521r1)
Biggest curve is best curve! — the clueless
https://www.youtube.com/watch?v=i_APoSfCYwU
Systems that choose P-521 often have an interesting threat model, even though said threat model is rarely formally specified.
It’s overwhelmingly likely that what eventually breaks the 256-bit elliptic curves will also break P-521 in short order: Cryptography Relevant Quantum Computers.
The only thing P-521 does against CRQCs that P-256 doesn’t is require more quantum memory. If you’re worried about QRQCs, you might want to look into hybrid post-quantum signature schemes.
If you’re choosing P-521 in your designs, you’re basically saying, “I want to have 256 bits of asymmetric cryptographic security, come hell or high water!” even though the 128-bit security level is likely just fine for your actual threats.
Aside: P-521 and 512-bit ECC Security
P-521 is not a typo, although people sometimes think it is. P-521 uses the Mersenne prime 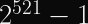
This has led to an unfortunate trend in cryptography media to map ECC key sizes to symmetric security levels that misleads people as to the relationship between the two. For example:
Regrettably, this is misleading, because plotting the ECC Key Size versus equivalent Symmetric Security isn’t a how ECDLP security works. The ratio of the exponents involved is totally linear; it doesn’t suddenly increase beyond 384-bit curves for a mysterious mathematical reason.
- 256-bit Curves target the 128-bit security level
- 384-bit Curves target the 192-bit security level
- 512-bit Curves target the 256-bit security level
- 521-bit Curves actually target the 260-bit security level, but that meets or exceeds the 256-bit security level, so that’s how the standards are interpreted
The reason for this boils down entirely to the best attack against the Elliptic Curve Discrete Logarithm Problem: Pollard’s Rho, which recovers the secret key from an 
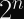
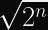
Taking the square root of a number is the same as halving its exponent, so the security level is half: 
Takeaway: If someone tells you that you need a 521-bit curve to meet the 256-bit security level, they are mistaken and it’s not their fault.

Why Not Use P-521?
It’s slow. Much slower than P-256 and Ed25519. Modestly slower than P-384.
Unlike P-384, you’re less likely to find an optimized, constant-time P-521 implementation.
Guidance for P-521
First, make a concerted effort to figure out the motivation for P-521 in your designs. Chances are, someone is putting too much emphasis on the wrong things for security.
If you use P-521, make sure you’re using it with SHA-512.
The standard NIST curve advice of RFC 6979 and point compression and/or hedged signatures applies here too.

Ed448 (EdDSA, Curve448)
Ed448 is the P-521 of the Edwards curves: It mostly exists to give standards committees a psychological comfort for the unlikely event that 256-bit ECC is desperately broken but ECC larger than 384 bits is somehow still safe.
https://twitter.com/dchest/status/703017144053833728
The very concept of having multiple “security levels” for raw cryptography primitives is mostly an artefact of the historical military roots of cryptography, rather than a serious consideration in the modern world.
Unfortunately, this leads to implementations that prioritize runtime algorithm selection negotiation, which maximizes the risk of protocol-level vulnerabilities. See also: JWT.
Ed448 was specified to use SHAKE256, which is a needlessly conservative decision which leads to an unnecessary performance bottleneck.
Why Not Use Ed448?
Aside from the performance hit mentioned previously, there’s no compelling reason to avoid Ed448 that isn’t also true of either Ed25519 or P-384.
Guidance for Ed448
If you want more speed, go with Ed25519. In addition to being faster, Ed25519 is also very widely supported.
If you need a prime-order field, use Decaf with Ed448 or consider P-384.
The Brainpool Curves
The main motivation for the Brainpool curves is that the NIST curves were not generated in a “verifiable pseudo-random way”.
The only reasons you’d ever want to support the Brainpool curves include:
- You think the NIST curves are somehow backdoored by the NSA
- You don’t appreciate small attack surfaces in cryptography libraries
- The German government told you to (see: compliance)
Most of the advice for the NIST Curves at each security level can be copy/pasted for the Brainpool curves, with one important caveat:
When considering real-world implementations, Brainpool curves are more likely to use the general purpose Big Number procedures (which aren’t always constant-time), rather than optimized assembly code, than the NIST curves are.
Therefore, my general guidance for the Brainpool curves is simply:
- Proceed at your own peril
- Consider hiring a cryptography engineer to study the implementation you’re relying on, especially with regard to timing attacks

Art: LvJ
Re-Examining the SafeCurves Criteria
Here’s a 2022 refresh of the SafeCurves criteria for all of the curves considered by this blog post.
| SafeCurve Criteria | Relevance to the Curves Listed Above |
|---|---|
| Fields | All relevant curves satisfy the requirements |
| Equations | All relevant curves satisfy the requirements |
| Base Points | All relevant curves satisfy the requirements |
| Rho | All relevant curves satisfy the requirements |
| Transfers | All relevant curves satisfy the requirements |
| Discriminants | Only secp256k1 doesn’t satisfy the requirements (out of the curves listed in this blog post) |
| Rigidity | The NIST curves do not meet this requirement. If you care about whether or not the standards were manipulated to insert a backdoor, rigidity matters to you. Otherwise, it’s not a deal-breaker. |
| Ladders | While a Montgomery ladder is beneficial for speed and implementation security, it isn’t strictly speaking required. This is an icing-on-the-cake consideration. |
| Twists | The only curve listed above that doesn’t meet the requirement is the 256-bit Brainpool curve (brainpoolp256t1). |
| Completeness | All relevant curves satisfy the requirements, as of 2015. SafeCurves is out of date here. |
| Indistinguishability | All relevant curves satisfy the requirements, as of 2014. |
SafeCurves continues to be a useful resource, especially if you stray from the guidance on this page.
For example: You wouldn’t want to use pairing-friendly curves for general purpose ECC digital signatures, because they’re suitable for specialized problems. SafeCurves correctly recommends not using BN(2,254).
However, SafeCurves is showing its age in 2022. BN curves still end up in digital signature protocol standards even though BLS-12-381 is clearly a better choice.
The Internet would benefit greatly for an updated SafeCurves that focuses on newer elliptic curve algorithms.

TL;DR
Ed25519 is great. NIST P-256 and P-384 are okay (with caveats). Anything else is questionable, and their parameter selection should come with a clear justification.
https://soatok.blog/2022/05/19/guidance-for-choosing-an-elliptic-curve-signature-algorithm-in-2022/
#asymmetricCryptography #BrainpoolCurves #cryptography #digitalSignatureAlgorithm #ECDSA #Ed25519 #Ed448 #EdDSA #ellipticCurveCryptography #P256 #P384 #P521 #secp256k1 #secp256r1 #secp384r1 #secp521r1 #SecurityGuidance
A question I get asked frequently is, “How did you learn cryptography?”I could certainly tell everyone my history as a self-taught programmer who discovered cryptography when, after my website for my indie game projects kept getting hacked, I was introduced to cryptographic hash functions… but I suspect the question folks want answered is, “How would you recommend I learn cryptography?” rather than my cautionary tale about poorly-implemented password hash being a gateway bug.
The Traditional Ways to Learn
There are two traditional ways to learn cryptography.If you want a book to augment your journey in either traditional path, I recommend Serious Cryptography by Jean-Philippe Aumasson.
Academic Cryptography
The traditional academic way to learn cryptography involves a lot of self-study about number theory, linear algebra, discrete mathematics, probability, permutations, and field theory.You’d typically start off with classical ciphers (Caesar, etc.) then work your way through the history of ciphers until you finally reach an introduction to the math underpinning RSA and Diffie-Hellman, and maybe taught about Schneier’s Law and cautioned to only use AES and SHA-2… and then you’re left to your own devices unless you pursue a degree in cryptography.
The end result of people carelessly exploring this path is a lot of designs like Telegram’s MTProto that do stupid things with exotic block cipher modes and misusing vanilla cryptographic hash functions as message authentication codes; often with textbook a.k.a. unpadded RSA, AES in ECB, CBC, or some rarely-used mode that the author had to write custom code to handle (using ECB mode under the hood), and (until recently) SHA-1.
People who decide to pursue cryptography as a serious academic discipline will not make these mistakes. They’re far too apt for the common mistakes. Instead, they run the risk of spending years involved in esoteric research about homomorphic encryption, cryptographic pairings, and other cool stuff that might not see real world deployment (outside of novel cryptocurrency hobby projects) for five or more years.
That is to say: Academia is a valid path to pursue, but it’s not for everyone.
If you want to explore this path, Cryptography I by Dan Boneh is a great starting point.
Security Industry-Driven Cryptography
The other traditional way to learn cryptography is to break existing cryptography implementations. This isn’t always as difficult as it may sound: Reverse engineering video games to defeat anti-cheat protections has led several of my friends into learning about cryptography.For security-minded folks, the best place to start is the CryptoPals challenges. Another alternative is CryptoHack.
There are also plenty of CTF events all year around, but they’re rarely a good cryptography learning exercise above what CryptoPals offers. (Though there are notable exceptions.)
A Practical Approach to Learning Cryptography
Art by Kyume.
If you’re coming from a computer programming background and want to learn cryptography, the traditional approaches carry the risk of Reasoning By Lego.
Instead, the approach I recommend is to start gaining experience with the safest, highest-level libraries and then slowly working your way down into the details.
This approach has two benefits:
- If you have to implement something while you’re still learning, your knowledge and experience is stilted towards “use something safe and secure” not “hack together something with Blowfish in ECB mode and MD5 because they’re familiar”.
- You can let your own curiosity guide your education rather than follow someone else’s study guide.
To illustrate what this looks like, here’s how a JavaScript developer might approach learning cryptography, starting from the most easy-mode library and drilling down into specifics.
Super Easy Mode: DholeCrypto
Disclaimer: This is my project.Dhole Crypto is an open source library, implemented in JavaScript and PHP and powered by libsodium, that tries to make security as easy as possible.
I designed Dhole Crypto for securing my own projects without increasing the cognitive load of anyone reviewing my code.
If you’re an experienced programmer, you should be able to successfully use Dhole Crypto in a Node.js/PHP project. If it does not come easy, that is a bug that should be fixed immediately.
Easy Mode: Libsodium
Using libsodium is slightly more involved than Dhole Crypto: Now you have to know what a nonce is, and take care to manage them carefully.Advantage: Your code will be faster than if you used Dhole Crypto.
Libsodium is still pretty easy. If you use this cheat sheet, you can implement something secure without much effort. If you deviate from the cheat sheet, pay careful attention to the documentation.
If you’re writing system software (i.e. programming in C), libsodium is an incredibly easy-to-use library.
Moderate Difficulty: Implementing Protocols
Let’s say you’re working on a project where libsodium is overkill, and you only need a few cryptography primitives and constructions (e.g. XChaCha20-Poly1305). A good example: In-browser JavaScript.Instead of forcing your users to download the entire Sodium library, you might opt to implement a compatible construction using JavaScript implementations of these primitives.
Since you have trusted implementations to test your construction against, this should be a comparatively low-risk effort (assuming the primitive implementations are also secure), but it’s not one that should be undertaken without all of the prior experience.
Note: At this stage you are not implementing the primitives, just using them.
Hard Difficulty: Designing Protocols and Constructions
Repeat after me: “I will not roll my own crypto before I’m ready.” Art by AtlasInu.
To distinguish: TLS and Noise are protocols. AES-GCM and XChaCha20-Poly1305 are constructions.
Once you’ve implemented protocols and constructions, the next step in your self-education is to design new ones.
Maybe you want to combine XChaCha20 with a MAC based on the BLAKE3 hash function, with some sort of SIV to make the whole shebang nonce-misuse resistant?
You wouldn’t want to dive headfirst into cryptography protocol/construction design without all of the prior experience.
Very Hard Mode: Implementing Cryptographic Primitives
It’s not so much that cryptography primitives are hard to implement. You could fit RC4 in a tweet before they raised the character limit to 280. (Don’t use RC4 though!)The hard part is that they’re hard to implement securely. See also: LadderLeak.
Usually when you get to this stage in your education, you will have also picked up one or both of the traditional paths to augment your understanding. If not, you really should.
Nightmare Mode: Designing Cryptography Primitives
A lot of people like to dive straight into this stage early in their education. This usually ends in tears.If you’ve mastered every step in my prescribed outline and pursued both of the traditional paths to the point that you have a novel published attack in a peer-reviewed journal (and mirrored on ePrint), then you’re probably ready for this stage.
Bonus: If you’re a furry and you become a cryptography expert, you can call yourself a cryptografur. If you had no other reason to learn cryptography, do it just for pun!
Header art by circuitslime.
https://soatok.blog/2020/06/10/how-to-learn-cryptography-as-a-programmer/
#cryptography #education #programming #Technology